企业价值评估中折现率相关参数的敏感性分析

2018-06-05胡晓明吴铖铖

会计之友 2018年9期

胡晓明吴铖铖

【摘要】收益法折现率作为企业估值的关键参数，其合理确定对运用收益法评估企业股权市场价值有着重要影响。文章选取沪深交易所2012—2016年披露的企业价值评估说明作为研究对象，从总样本、不同价值区间下部分样本两个视角，利用蒙特卡罗模拟详细分析各参数变动对评估价值的影响程度及其影响程度与评估价值之间的关系，研究表明：在折现率相关参数中，市场期望报酬率的变动对评估价值影响最大，且其影响程度与评估价值成反方向变动。文章可为评估实务提供参考借鉴，提高评估效率，提升参数测算的准确性及评估结果的公允性。

【关键词】蒙特卡罗模拟；企业价值评估；折现率；敏感性分析

【中图分类号】 F275 【文献标识码】 A 【文章编号】 1004-5937（2018）09-0009-04

一、引言

近年来，并购重组已成为我国经济生活领域的一个亮点，是推动我国经济结构调整和产业转型升级的加速器[1]，越来越多的企业通过并购重组发挥协同效应、降低交易成本、实现行业整合、改善基本面、持续提高经营能力[2-4]，从而增强市场竞争力[5]。同时，企业并购的核心是价值发现与价值创造[6]，企业价值评估可以提高并购重组交易定价的公允性[7-9]。上海证券交易所研究数据显示，2015年1月至2017年5月，A股市场共计891家公司宣告重大资产重组，其中844项重组采用评估价值作为定价依据，占比高达95%。从最终定价结果看，在以评估价值作为定价依据的重组项目中，217项重组标的最终交易价格直接以评估价值定价，占比达25.71%；30项重组标的最终交易价格为评估价值的九折，占比3.55%；97项重组标的最终交易价格为评估价值的1.1倍，占比11.49%，其余59.25%的重组项目标的资产最终交易价格介于评估价值的九折到1.1倍之间[10]，发现标的资产的评估价值可以在一定程度上左右并购重组的交易价格[11-12]。

在上市公司并购重组中，收益法逐渐成为企业价值评估的主流方法[13]，其在并购重组价值衡量中的地位不断提升。运用收益法评估企业价值时，折现率的测算一直是重点和难点，折现率的微小变动将会引起企业价值的巨大变动[14-16]。评估机构对折现率相关参数的确定原则已基本达成一致，同一通用性参数具有较强的可比性与趋同性[17-18]，但折现率作为收益法评估中一个极其重要的参数，其数值的合理性将会在很大程度上影响评估结果的准确性[13]。随着敏感性分析研究的深入与广泛应用，敏感性分析逐渐被用于判断投资项目中各种不确定因素对其经济评价指标的影响程度，从而预测项目能够承担的风险范围，为项目投资决策提供可靠的参考依据[19-20]。本文拟将敏感性分析方法从评估项目风险领域引入企业价值评估中，通过运用蒙特卡罗模拟对企业价值评估中折现率相关参数进行敏感性分析，揭示各参数对评估价值的影响程度及各参数影响程度与评估价值之间的变动关系，旨在建议评估师根据参数的敏感程度确定评估重点，如评估师应着重考虑并精确估算敏感程度大的参数，而减少统一性参数的估算时间，这样就可以大大提高评估效率，提升折现率相关参数测算结果与评估结果的准确性。

二、折现率敏感性分析模型与框架

（一）敏感性及其分析方法

敏感性可以表示为y=f（x1，x2，…，xn，）（xi为模型的第i个参数值），其原理为令每个参数在可能的取值范围内变动，研究和预测这些参数的变动对模型输出值的影响程度。敏感性分析的核心目的是分析各模型参数的敏感性系数大小，在实际应用中则重点考虑敏感性系数较大的参数，这样就可以大大降低模型的复杂程度，减少数据分析处理的工作量，并且可以在很大程度上提高模型的精确度。

敏感性分析可以根据建模方法的不同分为有模型和无模型两类。对于待解决的数据分析问题，如果清楚它的内部机理，且能够准确地将模型表示为y=f（x），则可以直接在此模型基础上进行敏感性分析。在实际问题中，面对庞大的数据，总是无法清楚地了解其内部规律，无法进行机理建模，早期的研究主要是借助统计知识来建立模型，如基于拉丁几何取样的多元回归方法、傅里叶敏感性检验法、方差分解法及利用非参数统计法进行敏感性分析的方法。随着研究领域内各种问题的出现，利用统计方法建模逐渐凸显它的局限性，当模型属性太多或者结果与属性之间是一种非线性关系时，统计方法处理结果的精度则达不到要求，所以采用人工神经网络的方法来建立模型逐渐被应用。神经网络模型只需要知道输入变量数据和输出数据，其自身能够对训练数据集进行训练和学习，用大量簡单的人工神经元模拟数据间的非线性关系，并能调节神经元之间的连接权重，以此建立能较好反映数据真实情况的网络结构，如Garson算法、随机化检验方法及MarkdownPad 2方法。

（二）敏感性分析模型

1.Pearson相关系数

基于Pearson的敏感性系数是建立在相关系数基础上的求解方法，该方法首先需要根据数据建立多因素线性回归模型，再利用公式计算出各不确定因素对指标值的敏感性系数。

ρ=■

该方法只适用于指标值与变量之间呈线性关系，如果指标值与变量之间不是线性关系，则利用上述公式计算出来的敏感性系数会出现一定的误差。

2.Spearman秩相关系数

由于基于Pearson的敏感性系数只适用于线性模型，因此提出适用于非线性模型的基于Spearman秩相关系数的敏感性系数计算方法。

ρ'=■

式中，ρ'表示Xi和Y的Spearman秩相关系数；X'■、Y'■表示Xi、Yi在排列后的数据排序，X'■、Y'■称为变量Xi、Yi的秩次。ρ'的符号表示变量X、Y之间的联系方向，其大小表示变量之间联系的紧密程度。若变量X和Y之间具有严格单调递增的关系时，ρ'=1，反之若变量X和Y之间具有严格单调递减的关系时，ρ'=-1。

当分别计算出影响因素X1，X2，…，Xn对指标值Y的秩相关系数ρ1，ρ2，…，ρn后，Spearman秩相关系数ρ1，ρ2，…，ρn就是影响因素X1，X2，…，Xn对指标值Y的的敏感性系数。

（三）折现率敏感性分析理论基础

假设以高顿增长模型计算股东权益价值，设D1为预期的未来第一年度实体现金流，r为与实体现金流相匹配的折现率（r=WACC），则企业整体价值V为：

V0=■

企业整体价值是企业未来现金流量根据加权平均资本成本WACC折现的结果，WACC为不含税盾折现率，只要企业整体价值保持不变，则其不随资本结构的变化而变化。

WACC=■×Rd×（1-T）+■×Re

在WACC模型中，权益资本成本Re的确定具有一定的复杂性，其为无风险收益率、企业的风险程度系数（β系数）与市场平均风险报酬率的乘积及企业特定风险系数三者之和，计算公式为：

Re=Rf+β（Rm-Rf）+Rc

企业整体价值对折现率的敏感程度可以表示为：

ε=■=■×■=-■=-（1+■）

由于g≥0，r>g，故有ε≤-1。由于现有评估实务和理论研究仅考虑折现率相关参数的敏感性大小，并未考虑增长率g对评估价值的影响，所以本文以零增长模型来分析评估价值对折现率相关参数的敏感程度，即g=0，ε=-1，可知企业整体价值与折现率成反方向变化，折现率越大，企业整体价值越低。由于折现率对评估价值的敏感性系数为-1，则折现率相关参数的敏感性系数绝对值均应小于1，即如果折现率的偏差幅度为1%，则评估价值偏差1%，但如果单个折现率相关参数的偏差幅度为1%，则评估价值的偏差幅度一定不会超过1%。

三、基于蒙特卡罗模拟的折现率相关参数敏感性分析

（一）蒙特卡罗模拟基本原理

蒙特卡罗模拟是以概率统计理论中的大数定律和中心极限定理为主要理论基础，以随机抽样为主要手段来模拟真实情况的一种方法。该方法的基本原理是假定函数Z=f（x1，x2，…，xn），其中变量x1，x2，…，xn的概率分布已知，利用抽样技术产生每一组随机变量x1，x2，…，xn的随机数值（xi1，xi2，…，xin），并将其代入函数模型得到函数值Z，按此步骤反复独立抽样N次，便可得到N个函数Zi（i=1，2，…，n），并得到函数的概率分布以及数学期望、方差等重要数学特征，评价指标函数的概率分布随模拟次数N的大小而变化，N越大，其分布越接近真实分布。

蒙特卡罗模拟可以直接模拟多个影响因素的不确定性，并能通过建立指标值函数模型将不确定性对其影响程度用概率分布的形式表现出来，克服了敏感性分析方法在多因素变化情况下的缺陷，适用于求解多因素变化的敏感性分析问题。

（二）折现率相关参数的描述性统计

通过对沪深交易所2012—2016年披露的企业价值评估说明进行统计，并剔除部分折现率相关参数缺失的样本，本文以剩下的88个有效样本中各参数的均值作为研究对象，在对折现率相关参数进行描述性统计的基础上，运用Crystal Ball软件对各参数进行敏感性分析。

从表1可以看出，2015年的评估样本数量为35个，占比达39.77%；2016年评估样本的数量为28个，占比达31.82%；2014年的评估样本数量为12个，占比达13.64%。从行业划分来看，制造业的样本数量最多，其数量为23个，占比26.14%；其次为信息传输、软件和信息技术服务业，样本数量为18个，占比20.45%；电力、热力、燃气及水生产供应业样本数量为13个，占比14.77%。

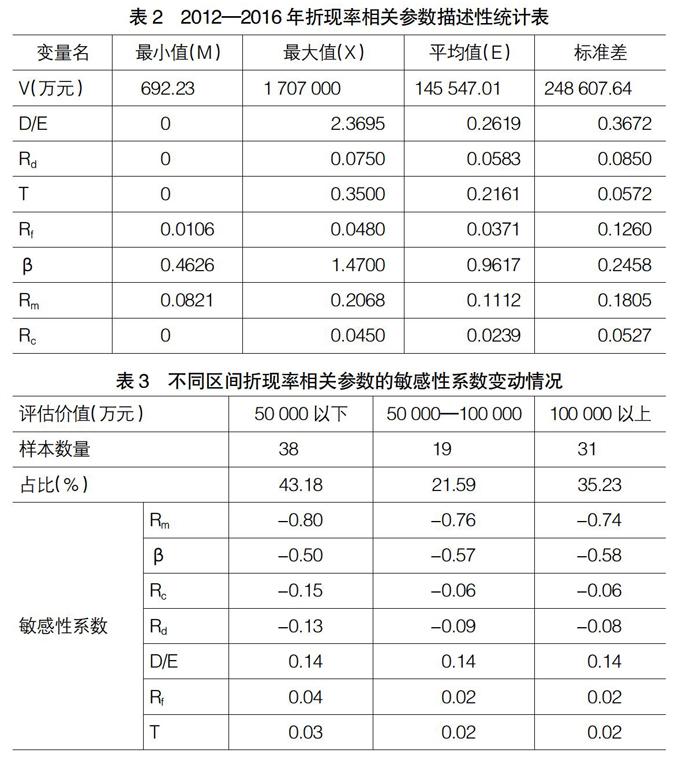
从表2可知，总样本中评估价值（V）的最大值为1 707 000万元，最小值为692.23万元，均值为145 547.01萬元，最大值与最小值之间差异较大。资本结构（D/E）的最小值为0（即企业无付息债务），最大值为2.3695，平均值为0.2619，且其标准差较大，说明各企业间的资本结构差异较大。公司特定风险系数的最大值为0.045，最小值为0，平均值为0.0239，说明各企业间的特定风险系数差异较小。从各参数的标准差来看，债务资本成本、所得税税率及无风险收益率的标准差均较小，说明这些参数的离散程度较小，均分布在其均值附近。

（三）不同区间折现率相关参数的敏感性分析

为探析各折现率相关参数对评估价值的影响程度及其与评估价值之间的关系，本文对88个有效样本按评估价值进行分段，分段结果表示评估价值在50 000万元以下的样本共38个，占比43.18%，评估价值的均值为24 921.98万元；评估价值介于50 000—100 000万元之间的样本共19个，占比21.59%，其均值为73 343.04万元；评估价值在100 000万元以上的样本共31个，占比35.23%，其均值为337 663.99万元。具体分析结果如表3所示。

通过分析可知，在各价值区间中，市场期望报酬率的敏感性系数均最大，表明其对评估价值的影响程度最高。当评估价值在50 000万元以下时，市场期望报酬率（Rm）的敏感性系数为-0.80；评估价值位于50 000—100 000万元之间时，市场期望报酬率（Rm）的敏感性系数为-0.76；评估价值在100 000万元以上时，市场期望报酬率的敏感性系数为-0.74，可知市场期望报酬率的敏感性系数绝对值与评估价值成反方向变动，即随着评估价值的增加，市场期望报酬率的敏感性系数绝对值越来越小，表明其对评估价值的影响程度越来越弱。对于β系数而言，其对评估价值的影响程度仅次于市场期望报酬率。当评估价值在50 000万元以下时，β系数的敏感性系数为-0.50；评估价值位于50 000—100 000万元之间时，β系数的敏感性系数为-0.57；评估价值在100 000万元以上时，β系数的敏感性系数为-0.58，可见β系数的敏感性系数绝对值与评估价值成同方向变动，即随着评估价值的增加，其敏感性系数绝对值越来越大，表明其对评估价值的影响程度越来越强。对于其他相关参数，如企业特定风险系数（Rc）、债务资本成本（Rd）、无风险收益率（Rf）和所得税税率（T），其敏感性系数绝对值与评估价值均成反方向变动，即评估价值增加时，其敏感性系数绝对值逐渐减小，说明其对评估价值的影响程度逐渐减弱。

（四）折现率相关参数的总体敏感性分析

在对折现率相关参数的敏感性系数与评估价值之间的变动关系进行分析后，本文通过运用蒙特卡罗模拟对总样本中折现率相关参数进行敏感性分析，揭示各参数变动对评估价值的影响程度。假设各相关参数均增加1%，以评估价值的均值作为计算基数来说明各参数变动对评估价值的相对影响和绝对影响（见表4）。

若各折现率相关参数发生相同幅度变动，可以发现其对评估价值的影响方向和影响程度各不相同。模拟分析可知，市场期望报酬率、β系数、公司特定风险系数及债务资本成本与评估价值负相关，其中市场期望报酬率的敏感性系数最大，其敏感性系数为-0.80，表明市场期望报酬率的变动对评估价值影响最大，市场期望报酬率的较小变动会引起评估价值较大程度的反方向变动。若市场期望报酬率增加1%，则会引起评估价值相对减少0.8%，即评估价值减少1 164.38万元。β系数的敏感性系数为-0.52，表明如果β系数增加1%，则评估价值相对减少0.52%，即减少756.84万元。在其他负相关参数中，公司特定风险系数敏感性系数为-0.15，债务资本成本敏感性系数为-0.12，其对评估价值的影响程度均低于市场期望报酬率和β系数。

资本结构、所得税税率、无风险收益率与评估价值正相关，其中对评估价值影响最大的为资本结构，其敏感性系数为0.12，表明如果资本结构增加1%，则评估价值相对增加0.12%，即评估价值增加174.66万元。所得税税率的敏感性系数为0.03，无风险收益率的敏感性系数为0.02，说明在评估价值正相关参数中，资本结构的变动对评估价值影响最大，而所得税税率和无风险收益率的变动几乎对评估结果没有影响。

四、结语

在运用收益法评估标的资产时，折现率相关参数的选取和确定存在难以预测、难以确定的问题，且有些参数需要根据评估人员的主观判断来确定，所以评估结果是否准确可靠，就需要评估人员准确确定评估参数并对参数进行一系列检验。敏感性分析可以测算评估结果的逻辑性，确保评估人员对价值驱动因素有更加详细的了解，使评估结果对信息使用者更具有参考价值。对折现率相关参数进行敏感性分析主要是为了确定影响评估价值的关键参数，要求评估人员在实际操作过程中需要重视关键参数的确定，从而提高评估效率和评估结果的准确性。本文选取沪深交易所2012—2016年披露的企业价值评估说明作为研究对象，以零增长模型作为研究基础，在不考虑增长率g对评估价值影响的情况下，通过研究后发现，评估价值对市场期望报酬率的敏感程度最高，但市场期望报酬率的敏感性系数绝对值与评估价值成反方向变动，β系数的敏感性系数绝对值与评估价值成同方向变动，即随着评估价值的增加，其对市场期望报酬率的敏感程度越来越弱，而对β系数的敏感程度越来越强。

【参考文献】

[1] 胡晓明，赵东阳，孔玉生，等.企业异质与可比公司赋权——基于并购的非上市公司估值模型构建与应用[J].会计研究，2013（11）：53-59.

[2] 上海证券交易所资本市场研究所.沪市上市公司2013年度重大资产重组专题分析报告[N].上海证券报，2014-06-05（B02）.

[3] 顾晓敏，孙爱丽.并购重组与价值创造：目标公司的协同效应分析[J].财会月刊，2015（34）：26-30.

[4] 王军辉，贾进，张晓婉.并购重组“双高”高温不退评估机构做优做强提供优质服务[J].中国资产评估，2016（10）：39-44.

[5] 李师.企业并购重组资产价值评估与交易价格关系研究[J].财会通讯，2014（8）：43-45.

[6] 李小荣，冉夢雅.并购重组中证监会关于资产评估反馈意见的分析[J].中国资产评估，2016（5）：29-33.

[7] 刘登清.评估机构在上市公司并购重组中的作用[J].中国资产评估，2014（1）：11-14.

[8] 王小荣，陈慧娴.企业并购重组中评估定价与成交价，谁被资本市场接受？——来自2007—2011年中国上市公司的经验数据[J].中央财经大学学报，2015（9）：55-62.

[9] 马海涛，李小荣，张帆.资产评估机构声誉与公司并购重组定价[J].中国软科学，2017（5）：101-118.

[10] 潘妙丽，张玮婷.上市公司并购重组资产评估相关问题研究[J].证券市场导报，2017（9）：12-18.

[11] 宋霞，郭涵予.我国上市公司并购重组价值评估方法的选择[J].财会月刊，2015（8）：22-25.