边坡稳定性计算方法的分析与探讨

邱志华 陈宝林

(1.福建省建筑科学研究院 福建福州 350025；2.福建省绿色建筑技术重点实验室 福建福州 350025)

0 引言

边坡工程已经成为各类土木工程建设中的重要组成部分[1]。在铁路、公路与水利建设中，存在大量的路基边坡与路堑边坡，而其稳定性严重影响了设施的安全运营与建设成本。目前对于边坡稳定分析主要还是根据传统的极限平衡法来进行。随着计算机技术的发展，出现了数值计算方法，其中有限元强度折减法应用最为广泛。而强度折减法分析问题的关键在于对边坡达到临界失稳状态如何判定。目前对于判定标准方法对比探讨较少，至今未形成统一的边坡失稳判断依据。为此，笔者分别对极限平衡法和有限元法应用于边坡失稳分析中的原理等进行对比分析研究，讨论各种判断依据的合理及适用性，拟建立边坡失稳状态的统一判断依据。

1 边坡的失稳破坏模式

许多边坡事故发生的主要原因是外界环境变化引起的岩土体强度降低[2]。边坡破坏主要表现为失稳和不均匀沉降。在工程中常发生整体失稳的情况，而且多出现在局部软基地段。边坡失稳的主要原因有两个：一是降雨时地表水下渗、浸泡使下渗范围内填土软化，抗剪强度降低，引起浅层填土圆弧形滑动失稳；二是填土与原地表界面在雨水下渗作用下抗滑力不足，致使填土层沿着原地表面滑动失稳。

2 边坡稳定分析极限平衡法

2.1 边坡稳定安全系数

传统的安全系数采用的定义为：

(1)

Bishop[3]提出具有强度储备性质的安全系数概念来评判边坡的整体稳定性。该方法具有一定安全储备的边坡外构筑一个虚拟边坡，其几何尺寸与真实边坡一致，但是其材料的强度指标均从c和φ折减为ce=c/K和tanφe=tanφ/K，此时滑面上的法向应力和剪切应力满足下式：

τ=ce+σntanφe

(2)

此方法在极限平衡法求解边坡稳定性当中获得了极大的成功，但极限平衡法对性质复杂的岩土路堑边坡，明确潜在滑裂面往往难以确定，而且诸如溃屈、倾倒等破坏类型还不能简单用极限平衡法。为此，在此基础上，人们求解边坡稳定安全系数的数值方法，并需要有个类似明确的概念来反映边坡的稳定程度，有限元强度折减技术正好解决这一难题。有限元强度折减中安全系数被定义为：使土体刚好达到临界状态极限破坏时对土体的抗剪强度进行折减的程度[4]。

强度折减有限元稳定系数的定义形式与所采用的强度屈服准则有关，对于M-C屈服准则：

(3)

(4)

对于广义Mises屈服准则，稳定系数定义如下：

(5)

式中：

α，k为材料参数；

I1为应力张量的第一不变量，I1=σ1+σ2+σ3；

J2为应力张量的第二不变量；

2.2 极限平衡法基本原理

运用极限平衡法时，需把土条假设成刚塑性体，根据静力学平衡条件和M-C破坏准则，建立整体力及力矩的平衡方程，进而求解某一假设滑动面上的稳定安全系数。基本思路是：对边坡进行条分后，在滑动土体n个土条中任取一条记为i。土条上的作用力有：土条本身自重Wi，水平作用力Qi，法向条间力Ei、Ei+1，切向条间力Xi、Xi+1，土条底面法向反力Ni和切向力Ti。当土条满足静力平衡条件，则其力矢多边形闭合，如图1所示。对于整体滑动体来说，为求得安全系数，需根据已知条件，结合平衡方程进行求解。而从各条块的平衡条件能得到方程远不及未知参数个数，因此方程组是高次超静定的，为使得方程得以有解，就需要作出一些简化的假定，使得未知参数减少或方程数量增加，使方程组转化为静定问题。基于不同的假定，便产生了各种不同的极限平衡条分法。如考虑部分条件力作用而不能满足力的平衡条件的Fellenius法和简化Bishop法等简易条分法；考虑条间力作用并能满足全部平衡条件的Janbu法和Morgenstern-Price法等严格条分法。

(a)边坡条分模型

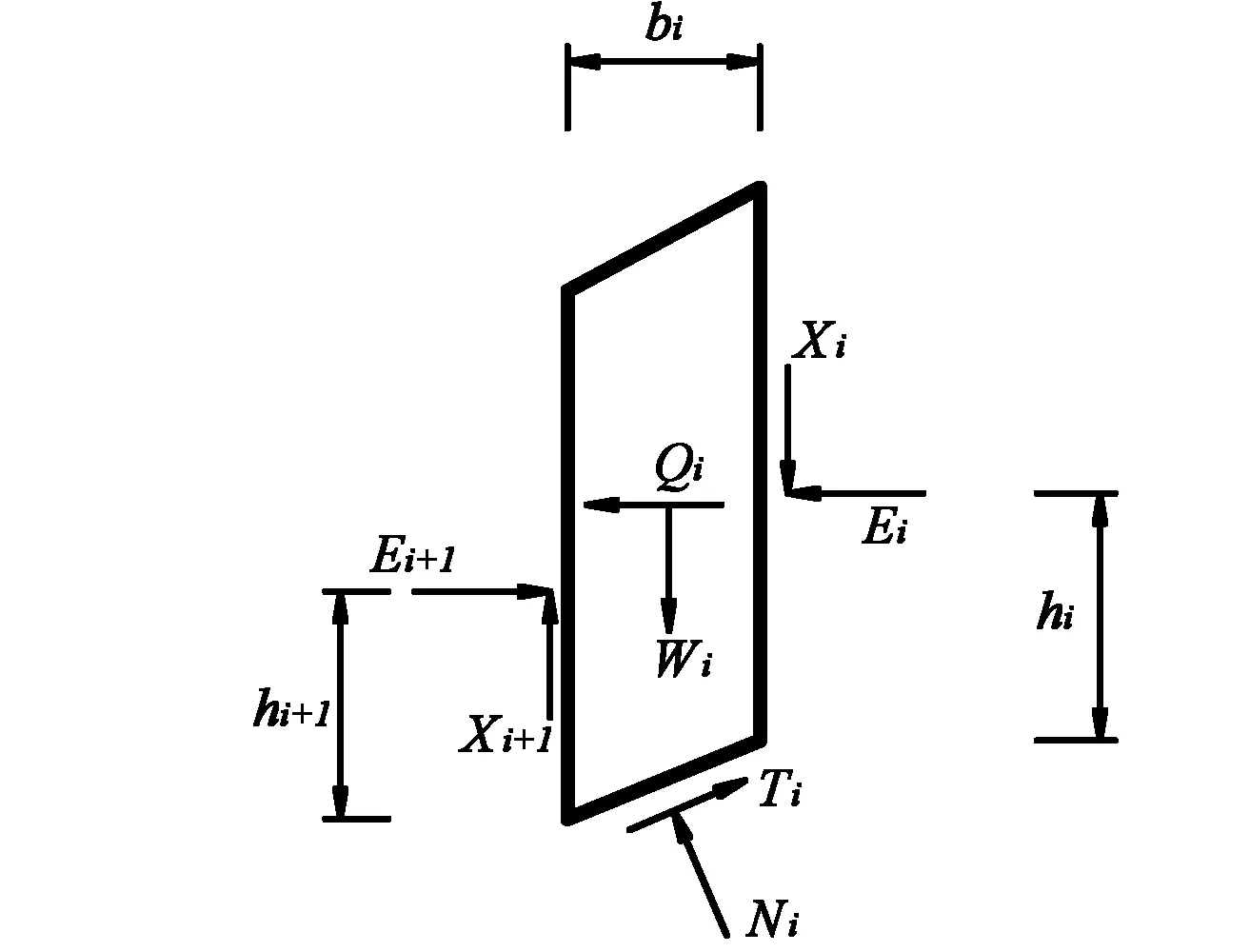
(b)条块作用力分析图1 边坡条分模型及作用力分析

3 边坡稳定分析的有限元强度折减法

极限平衡法存在着各种弊端，随着计算机技术的进步，有限元法在分析边坡稳定性上显示出了较大的优越性，对复杂边坡的变形破坏机理提供了更深层次的反映，能弥补一些极限平衡法上的不足。采用强度折减法对边坡安全系数的计算无须事先假定滑动面的形状和位置，能够反映岩土材料应力、变形等信息，并正逐渐成为新的趋势。

3.1 强度折减法原理及在ABAQUS中的实现

有限元强度折减法将强度折减技术、极限平衡原理与弹塑性有限元计算相结合，实质是一种不断改变强度参数的弹塑性有限元计算过程。其数值实现过程为：对土体强度参数按照某一给定的强度折减系数进行折减，折减后的强度参数可表示为土体实际发挥的强度，其计算式如式(6)、(7)所示。把折减后的强度参数输入边坡模型，利用逐级折减的方法对模型进行计算，直至分析结果表明边坡已失稳破坏。此时的折减系数就定义为边坡的稳定安全系数[5-6]。

φ′=arctan(tanφ/F)

(6)

c′=c/F

(7)

式中：c、φ分别为岩土材料的粘聚力和内摩擦角；

c′、φ′分别为经过折减后的粘聚力和内摩擦角；

F为折减系数。

ABAQUS中可以在Property模块中实现对材料强度的折减。通过设置场变量，建立场变量与材料强度参数的函数关系，实现材料参数随时间增量步变化，实现材料参数的折减，直至边坡临界破坏时，对应的折减系数即为边坡稳定安全系数[7]。

3.2 失稳评价标准的比较分析

采用有限元强度折减法分析边坡的稳定性需用失稳的评价标准来确定安全系数。目前有3种评价标准运用较广：①以有限元计算是否收敛；②以边坡特征部位位移是否发生突变；③以边坡中是否形成塑性应变的贯通区。

通过建立二维有限元折减法计算模型，对3种边坡稳定评价标准的可靠性和差异性进行对比探讨，并验证ABAQUS采用强度折减法计算安全系数的可靠性。

这里选择Dawson等[8]分析的一个均质土坡算例作为计算模型，具体尺寸如图2所示，土体重度γ=20kN/m3，弹性模量E=100MPa，泊松比μ=0.35，粘聚力c=13kPa，内摩擦角φ=20°，求坡角β分别为30°、35°、40°、45°、50°时边坡对应的安全系数。土体服从M-C屈服准则并采用理想线弹塑性模型，边界条件为：两侧边界约束水平位移，底边边界固定。按照3种稳定的评价标准计算边坡稳定安全系数，同时利用极限平衡法的简化Bishop法和Spencer法对同一算例进行计算，并对结果进行比较分析[9]。计算结果如表1所示。

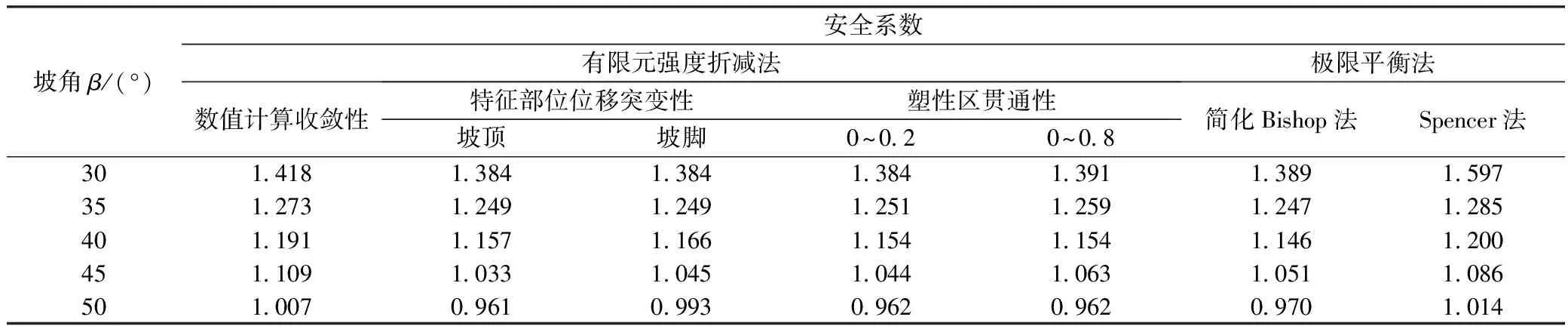
表1 安全系数计算结果

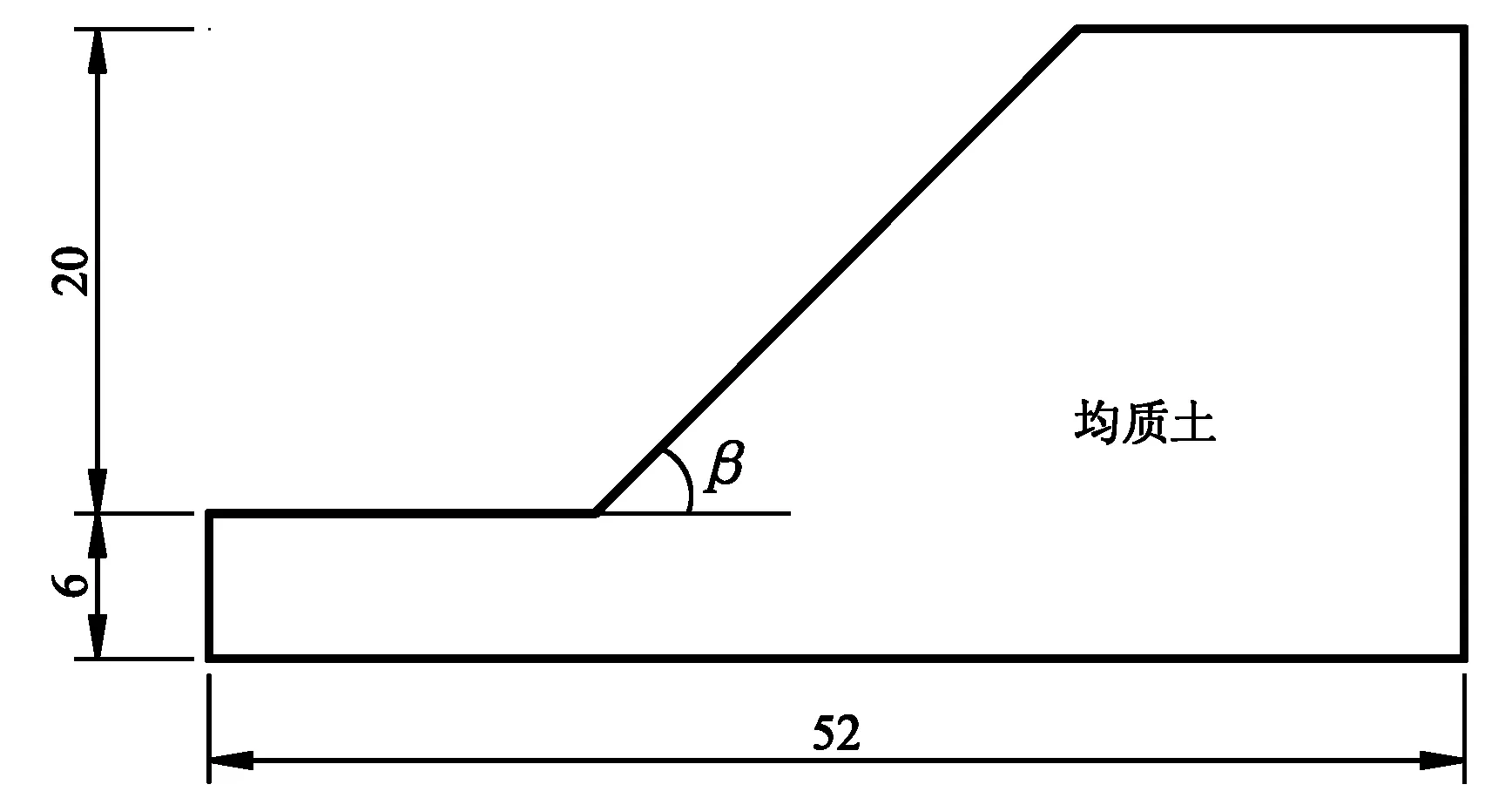
图2 有限元分析模型

(1)以有限元数值计算的收敛性作为判断依据计算的安全系数，方法简单，结果明确。所得结果均要比另外两种判断依据的结果来得大，与极限平衡法中的Spencer法较为接近，说明该方法有一定的合理性。但从边坡的变形破坏过程发现，当强度折减到一定程度时，虽然有限元计算能够收敛，但此时所得到边坡构形已严重失真，如图3所示。当数值计算不收敛时，边坡已完全扭曲，安全系数已没有意义。此外数值计算的收敛性还与收敛条件的设置、网格划分、计算模型的正确与否等有关，所以数值计算不收敛并不一定是边坡达到极限平衡状态引起的。因此，以数值计算的收敛性作为边坡失稳的评判标准可能会引起较大的误差甚至得出错误的结论。特别是在一些有加固体的边坡等复杂模型中应用应更加谨慎。

(2)以边坡特征部位的位移突变性作为边坡的失稳评判标准，步骤较为繁琐，拐点的选择具有主观性，特征部位的选取是关键。计算结果与极限平衡法的简化Bishop法接近，选取不同特征部位得到的安全系数有所差别，但差异较小。实践表明，边坡发生滑动以后，坡顶会明显下沉，而坡脚会向前挤出，因此建立坡顶点和坡脚点的位移与强度折减系数之间的关系曲线，根据曲线突变点估算安全系数，如图4所示。

β=30°(Fs=1.391)

β=40°(Fs=1.166)图3 边坡变形破坏示意图

β=35°(Fs =1.249)

β=45°(Fs=1.033)图4 边坡顶点和边坡脚点Fs-u关系曲线

该方法的分析过程与现实中边坡的破坏过程相近，可见该评价标准具有明确的工程实践意义，得到的安全系数也合理。由计算结果可以看出，特征部位的选取直接决定了对安全系数的判断，对于比较复杂的边坡，可能只发生一个或多个局部的失稳，此时，就要选取多个特征部位联合比较分析，特别在三维复杂边坡稳定分析中尤其关键。

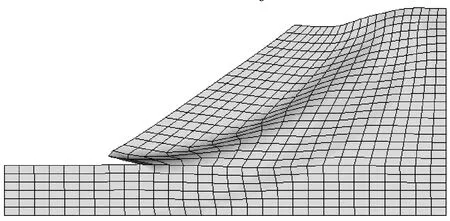
图5 边坡塑性区分布云图

(3)以塑性区贯通性作为边坡失稳的评判标准，方法较简单，边坡破坏较为直观，但其与软件后处理中塑性应变显示的精度有关。其结果与采用特征部位位移突变性和极限平衡法的简化Bishop法得到的安全系数都较为接近。按照弹塑性力学理论，当土体强度折减到一定程度，边坡土体的塑性变形发展直至相互贯通，此时边坡在外力作用下难以维持平衡，滑动面土体发生无限制的塑性流动，边坡沿着滑动面发生滑动而失稳。可见该评判标准具有明确的理论依据。但塑性区贯通时，由于进入塑性变形的土体受到周围未发生屈服土体的约束作用，边坡可能还未发生失稳，而且塑性区的范围还受土体材料参数、软件后处理中塑性应变显示精度的影响。如图5所示，

取不同的显示精度，其等效塑性应变等值云有较大的差别，即使在同一安全系数下，也会得出相反的的结论，显然是不合理的。因此以塑性区贯通性作为判定标准，难以获得合理、唯一的安全系数。

4 结论

(1)运用ABAQUS有限元软件并采用有限元强度折减法对边坡稳定性分析是合理可行的，能较好地获得边坡稳定安全系数和失稳边坡滑面的形状。同时采用有限元强度折减法对边坡稳定性的分析更加可靠。

(2)当强度折减系数与特征点水平位移关系曲线有明显拐点，此时等效塑性应变也形成贯通带，以其拐点作为边坡失稳临界状态是比较可靠的。因此，建议采用特征部位的位移是否发生突变联合塑性区，是否贯通作为边坡的失稳判断依据，尽量在坡顶和坡脚等特征部位设置多个观测点，同时设置合理的塑性应变显示精度，综合考察后得到边坡整体的安全系数和失稳滑动面。

参 考 文 献

[1] 李建林.边坡工程[M].重庆：重庆大学出版社，2013.

[2] 郑颖人，赵尚毅.边(滑)坡工程设计中安全系数的讨论[J].岩石力学与工程学报，2006，25(09)：1937-1940.

[3] Bishop A W.The use of the Slip Circle in the Stability Analysis of Slopes[J].Géotechnique，1955，5(1)：7-17.

[4] Duncan J M.State of the Art：Limit Equilibrium and Finite-Element Analysis of Slopes[J].Journal of Geotechnical Engineering，1996，122(7)：894.

[5] 沈珠江.计算土力学[M].上海：上海科技出版社，1990.

[6] 龚晓南.土工计算分析[M].北京：中国建筑工业出版社，2000.

[7] 费康，张建伟.ABAQUS在岩土工程中的应用[M].北京：中国水利水电出版社，2010.

[8] Dawson E M，Roth W H，Drescher A.Slope stability analysis by strength reduction[J].Géotechnique，1999，49(6)：835-840.

[9] 赵尚毅，郑颖人，时卫民，等.用有限元强度折减法求边坡稳定安全系数[J].岩土工程学报，2002，24(3)：343-346.