数学思想方法在初中数学合作学习模式中的应用

（新疆维吾尔自治区伊犁哈萨克自治州奎屯市125团中学 新疆奎屯 833203）

21世纪的今天，科技、经济等得到飞速的发展，为了顺应其高速的发展，国家急需综合素质过硬的人才。而初中教学是我国人才培养不可或缺的一个阶段，数学学科则是这一阶段的重要学习对象，同时，数学学科对较多的领域的发展有着至关重要的作用。如今，为顺应社会发展的需要，传统的初中数学教学模式已经相对落后，取而代之的是新型的合作学习模式。合作学习即以师为引导，学生为主体，通过团队合作的方式完成教学任务和目标。在此过程中，若师生充分发挥了数学思想的作用，并在实践中不断进行发展和完善，那么学生的学习必定能够取得事半功倍的效果。

一、数学思想方法在初中数学合作学习模式中的实际运用

合作学习模式是新课改背景下的全新的学习模式，而数学思想方法可以较好的在其中发挥作用。在实际的数学课堂教学中，充分运用到数学思想方法，对抽象的数学知识点进行整合、简化[1]。这样学生就能更加快速的领悟到数学的本质，能够高效的运用逻辑思维去解决数学问题。下面就以课堂中的若干教学事例进行分析：

1.化归转化思想的运用

所谓化归转化思想是指并不直接对原来的问题进行解答，而是另辟蹊径，想方设法对其进行变形，直至将其转化成某些已知的问题。通过转化可以发掘出隐含的因素，拉近已知条件和结论的距离，找出它们的内在联系，帮助更快的解决问题。例：

如图（1），梯形ABCD中，AD∥BC，AB=CD，对角线AC、BD相交于O点，且AC⊥BD，AD=3，BC=5，求AC的长。

解：过D作DE⊥AC交BC的延长线于E，则AD=CE、AC=DE。所以，BE=BC+CE=8.因为AC⊥BD，所以BD⊥DE。因为AB=CD，所 以AC=BD。 所 以GD=DE。 在RT△BDE中，BD²+DE²=BE2所 以

解题思路：此题是由梯形对角线互相垂直的特点通过平移对角线将梯形问题转化为三角形和平行四边形问题，最终问题得到解决。

2.数形结合的思想和方法的运用

数形结合即在分析、研究和解决问题的时候将数（量）与（图）形结合起来的一种思维方法。数形结合的途径主要有：①形转化为数；②数转化为形；③数形结合。

（图形隐含条件）例：

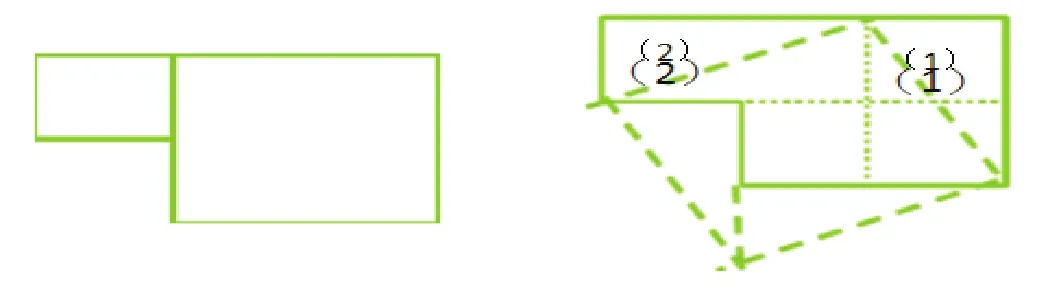
图（2）

如图（2）是连接在一起的两个正方形，小正方形的边长为大正方形边长的½。问：若只允许剪两刀，应如何裁剪才能拼成一个新的大正方形？

对于这道题，大部分的学生采取实际操作的方法，这里剪一下，那里剪一下，但总是达不到想要的效果，拼凑不出一个完整的大正方形。我们打破常规思维就不难发现，从已知到结论，虽然图形在发生变化，但是图形的总面积却不变。假设小正方形的面积为1，则其边长为1，大正方形的边长为2，则可知新大正方形的面积为5，边长为，如此我们只需要沿着图（2）中的线段去裁剪即可，答案就浮出水面了。

3.配方法的运用

配方法主要有以下几种出题形式：（1）用配方法解方程；（2）利用配方法比较代数式大小；（3）配方法用于求最大值、最小值；4.利用配方法确定二次根式中字母的取值范围；5.配方法用于证明。以配方法解方程为例：

已知方程2x2+x-1=0.求未知数x的值。解析：方程的两边都除以2，得到，移项得，配方得即。开方，得

二、数学思想方法在初中数学合作学习中的长处

1.多元化学生合作学习的方法

在初中数学的学习过程中采取合作学习的方式方法，可以加强学生之间的沟通和交流，帮助学生互相学习、共同进步，在不断的沟通与交流中迸发新的思维火花。把数学思维方法充分运用于合作学习中，也有利于学生逆向思维能力的发展，进行发散思维，学会举一反三、触类旁通。如此，学生合作学习的方法在原有的基础上就可以得到升华，从正向、逆向综合的进行考虑问题，多元化学生的合作学习方法[2]。

2.科学化学生的学习观念

就大部分学生的传统的学习观念来说，有严重的不足与缺陷，思想僵化、固守成规。而学生的学习效果则是内部、外部两方面的因素共同作用的结果，在新课改的背景下，教师的教学方式的得到了很大的改善，日渐科学化、合理化，此时学生自身的思维习惯、学习观念也应跟上步伐，打破常规，合理运用数学思维方法，科学进行合作学习。如此，数学思维方法就帮助了学生打破陈旧的学习观念，做到了与时俱进，培养了学生的数学思维能力。

3.强化初中数学的教学质量

题海战术一直是过去人们学习数学的思想，而这一思想恰恰是错误的，而在初中数学的合作学习中充分运用数学思想方法则可以很好的解决这一问题[3]。除此之外，数学思想方法，还可以改变教师在授课中不深入展开教学内容的陋习，教师不再是照本宣科，而是在课本的基础上循循善诱，把学生带入数学领域更深层次的境界。借助数学思维方法，教师可以充分的发掘教学内容，丰富解题技巧和思维方法，倾心打造适合学生们的教案，提高学生的逆向、正向思维能力，从而达到提高教学质量的目的。

综上所述，事物是不断变化和发展的，教育观念也在不断的更新和变化，而这一切的最终目的都是为了更好的教育学生，帮助学生更好的学习数学知识和其他学科的知识。数学思想方法的运用不仅是数学学科教育创新发展的成果，也是教育理论的延伸。无论从哪方面着眼，我们的宗旨都是为学生们创造更适宜他们的、科学的课堂。

[1].朱义华.数学思想方法在初中数学合作学习模式中的应用[J].文理导航(中旬),2015(03)：24.

[2]赵圣柱.数学思想方法在初中数学合作学习模式中的应用[J].新课程(中学),2016(04)：130.