两步自适应快速滤波算法测量火箭弹滚转角*

闫小龙，陈国光，田晓丽, 董晓芬，赵福春

(1 中北大学，太原 030051； 2 山东特种工业集团有限公司，山东淄博 255201)

0 引言

在制导火箭弹的飞行过程中，为了准确对火箭弹的飞行轨迹进行控制，姿态角的获取是非常重要的。如今使用陀螺仪、星敏传感器、GPS以及磁强计来测量滚转姿态角[1]。磁强计以成本低，受外界干扰小而被广泛应用。然而，这种传感器测姿时存在较多的误差因素，限制了滚转角测量的精度。因此，在正确测量火箭弹滚转角前，必须对磁强计及测量电路进行校准补偿。目前，研究人员已经提出了很多的解决方案。黄琳等人使用UKF滤波方法离线校准磁传感器的灵敏度偏差，从而给出每个磁传感器对应的补偿值[2]。Da Forno等人分别使用UKF与EKF对磁强计的灵敏度和基线偏移进行在线校准[3]。卢兆兴等人提出使用自适应遗传算法校准磁强计的灵敏度[4]。文中提出的算法对双轴磁强计的测量幅值、双轴基线偏移、灵敏度、非正交角进行在线校准。磁强计五个参数的校准使测量值更为准确；两步快速算法使得在线快速校准成为可能。

1 滚转姿态角测量模型

使用双轴磁强计测量制导火箭弹滚转角时，在火箭弹横截面上安装了双轴磁强计测量组件。通过角度关系的转换，可以得到火箭弹的滚转姿态角。

图1是基于磁强计的角度测量模型。红色方块代表双轴磁强计测量组件。其中，O-xynz为测量坐标系，OX为弹轴矢量，Oy和Oz是磁强计的两个理论正交的敏感轴。δ是非正交误差角，OZm为载体零位参考轴，OZ为惯性空间零位参考轴，Hyz是火箭弹当地地磁场矢量在Oyz上的投影，由全球地磁场模型给出，γ为载体旋转姿态角。φ0是磁强计的安装误差角，φ是制导火箭弹的滚转姿态角。

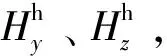
(1)

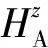
记φs=φ-φ0，则

(2)

火箭弹的滚转姿态角可得

γ=αH-φ0-φs

(3)

通过滤波方法估计参数实际上是将参数估计的问题转化为状态估计的问题，可以将滤波过程中关注的参数增加到状态向量中，在滤波过程中实时估计，根据滤波的状态向量与设定真值进行对比，从而判断滤波过程及结果的正确性。

滤波的系统状态方程与量测方程如式(4)和式(5)所示：

Xk+1=f(Xk,uk)+Wk

(4)

Hk+1=h(Xk+1)+Vk+1

(5)

式中：Xk+1为状态向量，Hk+1为量测向量。f为线性向量函数，h为非线性向量函数，Wk为系统方程噪声向量，Vk+1为量测方程噪声向量，uk为确定性控制项[5]。

滤波过程中被估计的参数向量为：

(6)

为了准确而精简地描述火箭弹的滚转运动，考虑到火箭弹在飞行过程中所需要的飞行参数以及在飞行过程中的加速度变化很小，所以这里假设火箭弹的滚转运动为加速度缓慢变化的加速运动。

(7)

在公式(7)中，Φ,Φ′,Φ″分别代表火箭弹的滚转角位移，角速度和角加速度，下标“i”表示第i个采样周期对应的数据。

2 滤波器初值的两步快速自适应调整

在卡尔曼滤波算法中，状态向量初值的准确性决定着滤波器的收敛速度[6]。然而，由于不同的磁强计，不同的安装方法及安装工艺导致状态向量中的参数具有不同的真值，所以状态向量的初值是不确定的。为了加快滤波器的收敛速度，需要将滤波器的初值尽可能快的精确到一个较小的范围内。

2.1 第一步：磁强计校准参数的快速调整

捷联在弹体截面上的双轴磁强计在火箭弹飞行时，Y轴和Z轴的轨迹方程为：

(8)

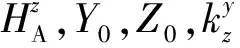
在这一步骤中，校正参数拟合的精度越高，意味着UKF收敛速度越快，但是拟合精度的提高与拟合时间的消耗并非成正比关系。因此，当拟合精度提高的速度接近滤波器收敛的速度时需要适当的判断条件来终止这一过程。

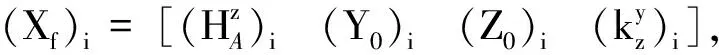
(Λf)i=(Xf)i-(Xf)i-1

(9)

拟合参数的协方差矩阵为:

(10)

2.2 第二步：滚转运动的快速调整

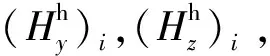
(11)

结合式(7)有下列关系：

(12)

同样，在考虑解算速度要求高于解算精度要求的前提下，当滚转角参数残差最小时取为滤波初值，对Φ,Φ′,Φ″进行参数拟合，定义残差为：

(13)

当ε取到最小值时，火箭弹的滚转参数Φ,Φ′,Φ″取得最优值。

与第一步相同，在第二步中，参数拟合的精度与拟合的时间并非成正比。当拟合精度提高的速度接近滤波收敛的速度时需要一个类似的停止策略。

(Λs)i=(Xs)i-(Xs)i-1

(14)

拟合参数的协方差为：

(15)

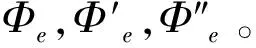
3 具有加性噪声的增强无迹卡尔曼滤波算法

为了提高现有滤波算法的性能，文中提出了快速收敛噪声隐含的扩维无迹卡尔曼滤波算法。文中提出新的TAUKF算法，该算法在UKF中包含模型误差预测，增加了系统状态下的驱动噪声，以扩大系统状态的输入信息。所提出的算法克服了传统UKF系统模型误差对滤波性能的影响，增强了滤波过程的鲁棒性。扩展系统状态，增加了UKF模型中状态向量的维数。考虑到驱动噪声对系统运动模型的影响，噪声被加到系统状态中。因此，扩展状态向量和协方差矩阵可以表示为：

(16)

(17)

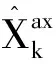
(18)

(19)

(20)

时间传播方程为：

(21)

(22)

状态估计方程为：

(23)

(24)

量测估计方程为：

(25)

(26)

互协方差矩阵为：

(27)

计算UKF增益：

(28)

最后，更新状态矩阵和协方差矩阵：

(29)

4 算法模拟仿真

测量火箭弹的滚转运动，对磁强计和测量电路进行仿真建模。火箭弹在实际飞行过程中，磁强计和测量电路的工作参数不能准确的获取。而在模拟过程中，这些误差参数都可以进行人为调整。只有这样才能将最终的数据处理结果与正确的数据进行对比，用来评估算法的优势。

分别使用传统UKF方法和文中提出的TAUKF算法对磁场测量组件进行参数校准和火箭弹的角度测量。

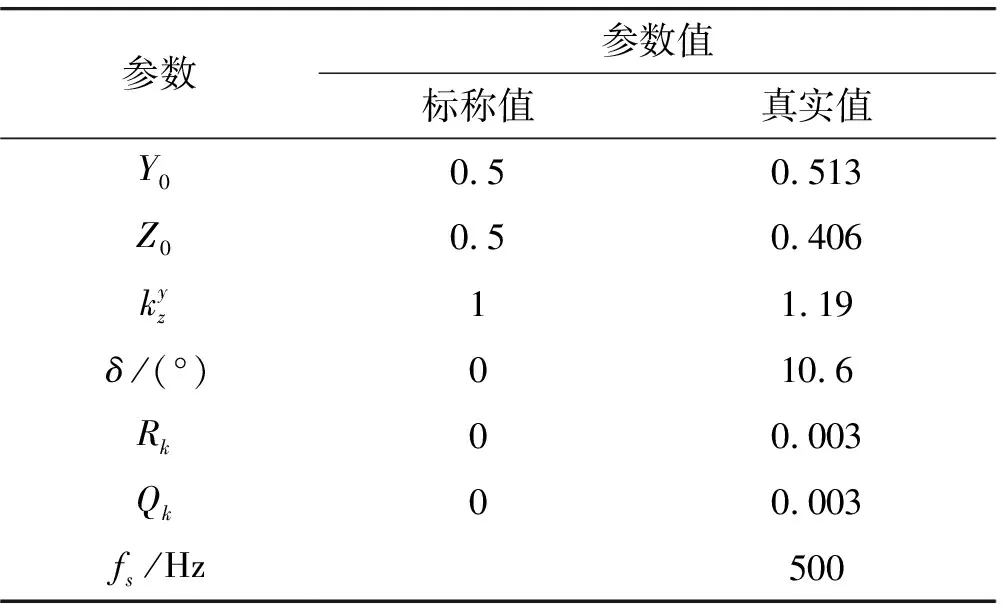
参数参数值标称值真实值Y00.50.513Z00.50.406kyz11.19δ/(°)010.6Rk00.003Qk00.003fs/Hz500

由图2(图中FS为“Full Scale”的缩写，代表满量程)我们可以看到，TAUKF在0.11 s左右完成了滤波算法的初值拟合，并将滤波算法的初值调整到非常接近真值的精度。在后续滤波阶段大约0.15 s左右，滤波器状态向量中校正参数接近真值，校正参数值设为最优恒定值。开始小计算量的UKF滤波。通过对比可以看出，TAUKF较UKF在收敛速度上有着较明显的优势。

在滚转角信息的输出结果看来，提出的TAUKF算法同样在收敛速度上要远远的高于现有的UKF算法。并且在500 Hz采样频率的前提下，提出的TAUKF算法可以在接收数据0.17 s左右就可以提供0.023 rad精度的角位移，0.07 rad/s精度的角速度，以及0.08 rad/s2精度的角加速度。而传统的UKF算法想要提供该精度下的滚转角信息则需要49 s左右的信号处理时间。

5 结论

在该研究中，提出了一种TAUKF滤波算法，用于在线快速估计火箭弹的滚转姿态角。有效地解决了旋转导弹在发射后不能及时获取滚转姿态而无法机动的问题。该算法通过对磁场测量组件的校正参数的确定，以及实时的量测结果，计算火箭弹的滚转姿态角。在滚转姿态角的实时处理过程中，该算法对滤波器的初值进行自适应获取，极大的加快了滤波器的收敛速度与精度。并且在磁场测量组件的校正参数确定后，对滤波器的状态向量的校正参数赋予确定值，在很大程度上减少了弹载计算机的运算量，为弹上其他信息的计算留出空间。