半主动悬架PID控制与Fuzzy-PID控制对比研究*
2018-06-04龙海洋李耀刚戚冬达董珈皓
苗 壮,龙海洋,李耀刚,戚冬达,董珈皓
(华北理工大学 机械工程学院,河北 唐山 063210)
0 引言
悬架作为影响车辆综合性能的关键部件,连接车身与车桥,起着缓解车辆在路面行驶时由于路面凹凸不平、发动机自身振动以及转弯制动等操作引起的车身振动的作用[1]。半主动悬架系统中存在可调阻尼力器件,在控制策略下动态调节阻尼力以减少车身振动,以提高乘坐舒适性和操作稳定性[2]。
半主动悬架之所以能提升悬架性能,其关键在于设计了行之有效的控制策略。PID控制算法简单、易于实现,适用于车辆悬架的半主动控制;另外常规PID控制与Fuzzy(模糊)控制结合可以实现参数动态调节,以应对半主动悬架的非线性和时变特性。笔者基于上述两种控制方法,分别对半主动悬架设计PID控制和Fuzzy-PID控制策略,并以被动悬架性能为参考,对比研究两种控制方法对于悬架性能的改善情况。
1 四分之一半主动悬架模型
悬架是非线性的时变系统,在对其进行仿真研究时,需首先对这一复杂系统进行简化[3]。其中,二自由度四分之一悬架模型简单,且能充分反映悬架各项主要性能指标,本次研究均基于该种简化模型,如图1所示。
动力学微分方程如式(1):

(1)
其中:m1为轮胎质量;m2为车身质量;z2为车身垂直位移;z1为轮胎垂直位移;k1为轮胎刚度系数;k2为悬架刚度系数;c为悬架减振弹簧刚度;q为路面输入;F为可调阻尼力,也是半主动控制策略的研究对象,使其实现动态调节来提升悬架性能。

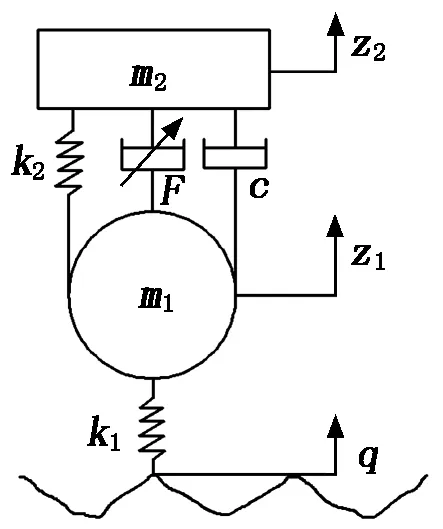
图1 四分之一半主动悬架
该系统的状态方程和输出方程为:
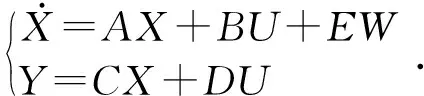
(2)
其中
U=[F];W=[q].
基于式(1)所示的四分之一车半主动悬架微分方程与式(2)的状态方程和输出方程,在Simulink中创建如图2所示仿真模型。当去除可调阻尼力F后,该模型即变为被动悬架仿真模型。本文选用某款车型悬架参数为:m1=30 kg,m2=264 kg,k1=160 000 N/m,k2=16 000 N/m,c=1 100 N·s/m。
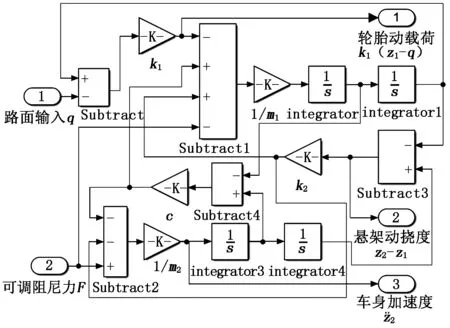
图2 半主动悬架仿真模型
2 随机路面输入模型
车辆在行进过程中,会受到由于地面凹凸变化、发动机自身振动、转弯制动等操作引发的车身振动。其中,不平路面激励是最主要的激励,在研究汽车悬架动态性能时,必须建立有效的路面输入模型[4]。
在对悬架性能进行仿真研究时,路面输入通常采用简谐振动信号和白噪声信号[5]。本文采用白噪声法模拟路面输入,其微分方程如式(3)所示:
(3)
其中:q(t)为随机路面激励;w(t)为高斯白噪声信号;n0为参考空间频率;v为车辆行驶速度,m/s;Gq(n0)为路面谱值,其数值可查询国家标准;f0为空间截止频率。
基于式(3),在Simulink中建立随机路面仿真模型,如图3所示。
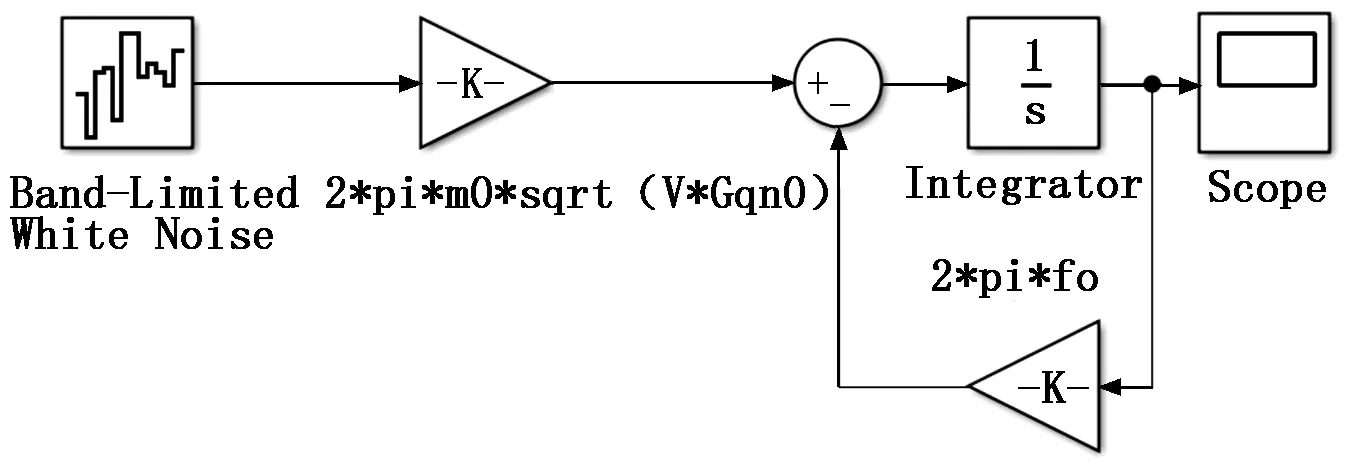
图3 随机路面输入模型
3 半主动悬架PID控制
PID控制以被控对象的偏差作为输入,经过比例(P)环节、积分(I)环节、微分(D)环节组合得到控制量[6],其原理如图4所示。
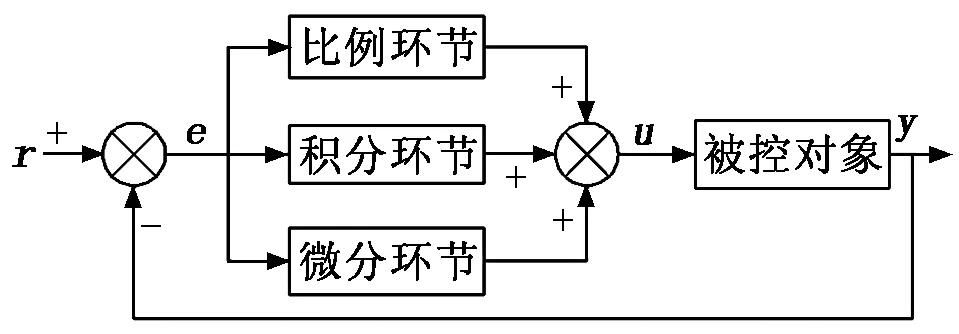
图4 PID控制原理图
PID控制算法表达式如下:
(4)
其中:u(t)为控制器的输出量;e(t)为被控对象预设值r(t)和真实值y(t)的差值;kp为比例系数;ki为积分系数;kd为微分系数。
本次半主动悬架PID控制研究中,以降低最能反映乘坐舒适性的车身垂向加速度为控制目标,其真实值和预设值的差值输入至PID控制器进行比例、积分、微分运算,预设值设置为零,期望车身垂向加速度无限趋近于零,可调阻尼力F作为PID控制的控制量。在Simulink中创建半主动悬架的PID控制仿真模型,如图5所示。
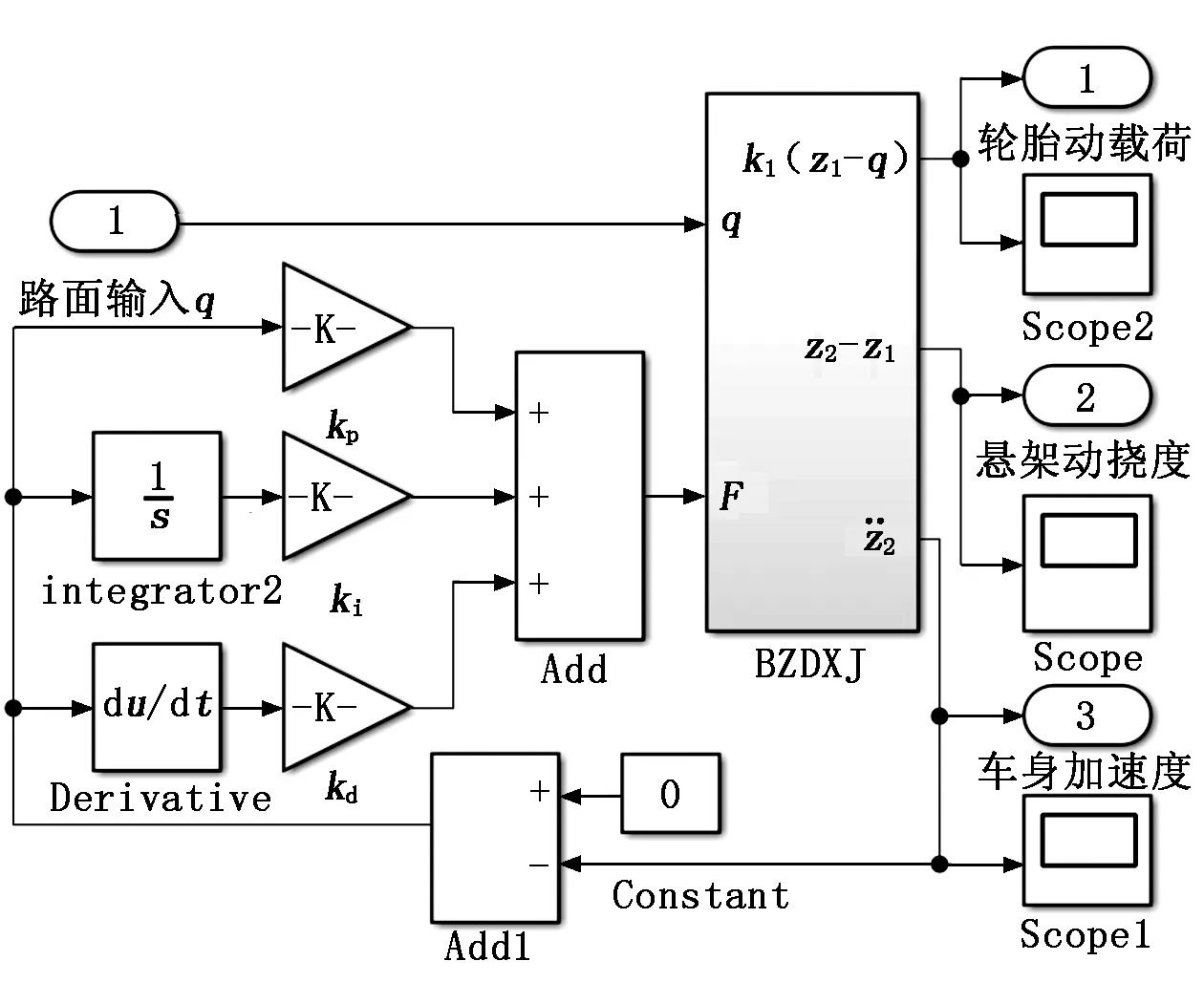
图5 半主动悬架的PID控制仿真模型
本次研究采用典型的试凑法对PID控制参数kp、ki、kd进行确定,先调节比例系数,后调节积分系数,最后调节微分系数,同时观察悬架动态响应。经过反复调试,得到控制系数kp=150,ki=1,kd=0.1。
4 半主动悬架Fuzzy-PID控制
半主动悬架系统作为非线性的时变系统,常规PID控制呈现出了参数不可动态调节的缺点,因此出现了PID控制与其他控制方法结合的复合控制方法[7]。本次研究将PID控制与Fuzzy控制结合起来,形成Fuzzy-PID控制,其原理如图6所示,利用Fuzzy理论实现对PID控制参数实时更正,以满足悬架系统的时变特性,从而达到更好的控制效果。
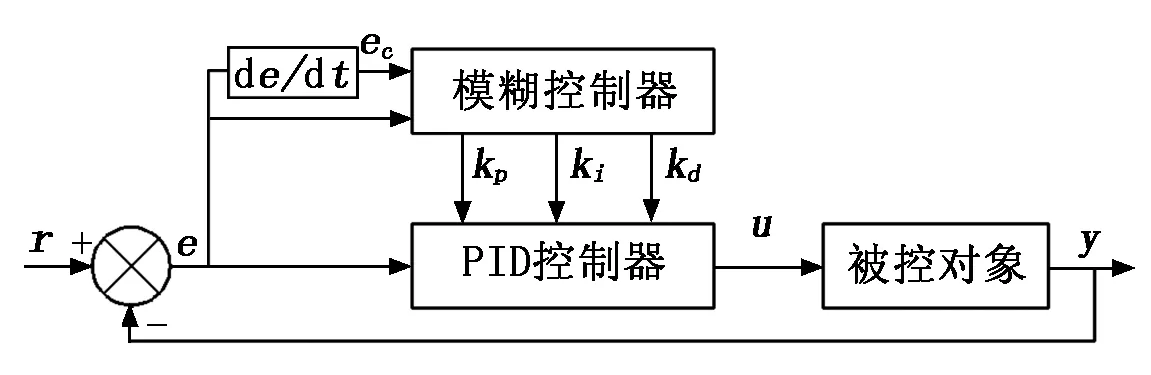
图6 Fuzzy-PID控制原理图
本次悬架Fuzzy-PID控制中,选取车身垂向速度真实值和预设值之差e以及其变化率ec作为模糊控制器的输入。设置预设值为零,此时e即为车身垂向速度,ec即为车身垂向加速度。模糊控制器的输出为PID控制器的三项参数的调节量Δkp、Δki、Δkd,再经由PID控制器,得到最终的kp、ki、kd,输出为可调阻尼力F。其中kp、ki、kd与Δkp、Δki、Δkd关系如下:
(5)
其中:kp0、ki0、kd0为整定前的初始参数,其数值选用常规PID控制得到的最佳参数;Δkp、Δki、Δkd为比例、积分、微分系数调节量;kp、ki、kd为最终的PID控制器参数。
实际生活中,车身垂向速度的大致区间为[-0.3,0.3] m/s,车身垂向加速度大致区间为[-3,3] m/s2。输入输出的模糊论域如下:
e,ec=[-3,-2,-1,0,1,2,3].
Δkp,Δki,Δkd=[0,1,2,3].
输入和输出变量均选用三角形隶属函数,模糊推理采用Mamdani法,共建立3×49条控制规则;解模糊则采用重心法,基于以上设计创建仿真模型如图7所示。
5 仿真分析
设置相同的车速,在同一路面情况下,对被动悬架、所设计的PID控制和Fuzzy-PID控制半主动悬架仿真并观察性能响应情况。我国的路面情况以B级和C级为主,选取B级路面,查询国家标准得此时路面谱的几何平均值为64×10-6m3,参考空间频率取0.1 m-1,空间截止频率取0.01 Hz,设置车速为25 m/s,仿真时间5 s。三种悬架控制策略下悬架动挠度、车身垂向加速度、轮胎动载荷时域响应如图8所示。然后求出各项指标的均方根,如表1所示。
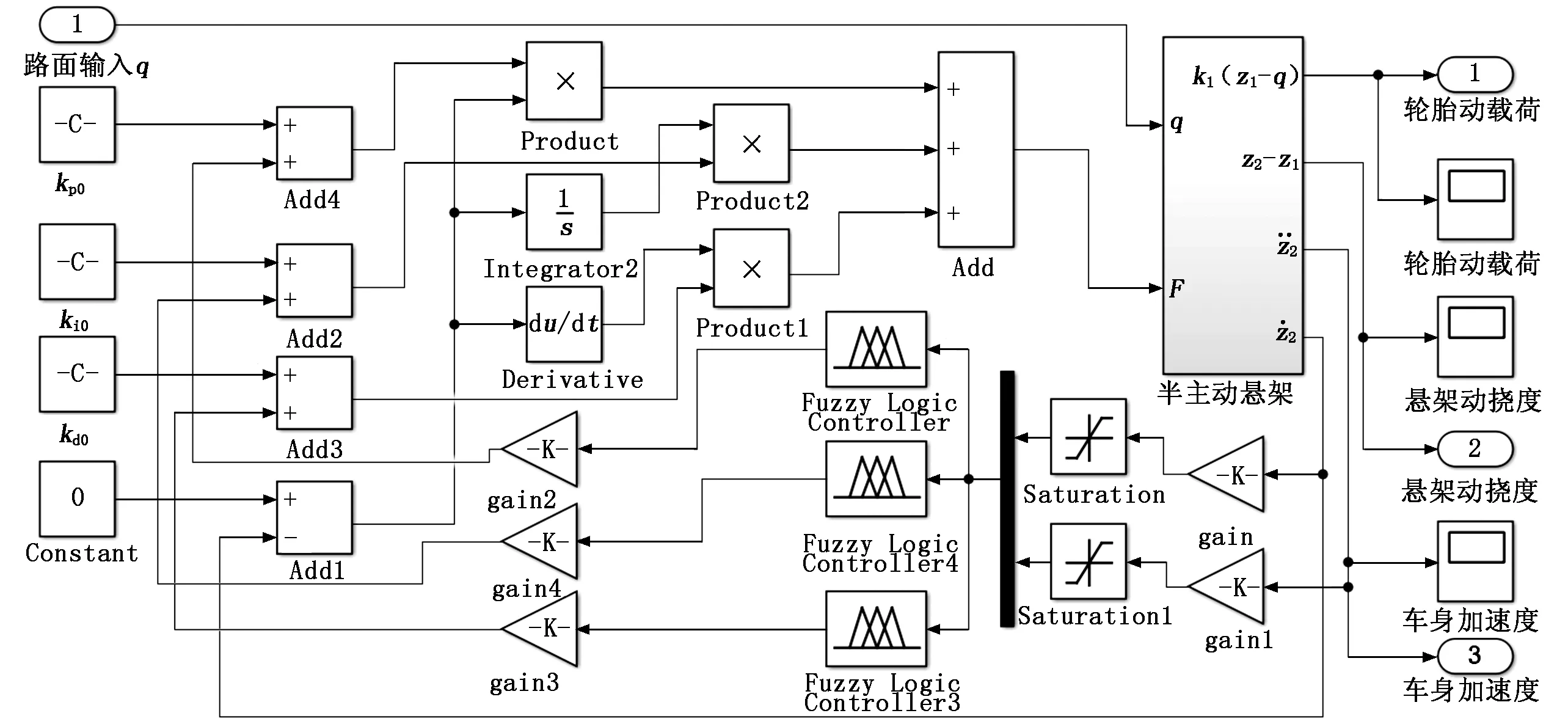
图7 半主动悬架Fuzzy-PID仿真模型

图8 悬架三指标仿真结果
观察图8和表1可得,当车辆以25 m/s行进在B级路面时,相比被动悬架,本次设计的常规PID控制和Fuzyy-PID控制下的半主动悬架性能响应曲线的峰值均有所下降。轮胎动载荷、悬架动挠度、车身垂向加速度的均方根在常规PID控制下分别降低了4.8%、8.6%、9.3%,Fuzzy-PID控制使悬架三项性能指标分别降低了13.5%、26.5%、27.2%。

表1 悬架性能指标均方根
6 结论
本文首先对汽车悬架进行简化得到二自由度四分之一半主动悬架模型,并利用积分白噪声法建立路面输入模型。然后以降低悬架主要性能指标即轮胎动载荷、悬架动挠度、车身垂向加速度为目的,对半主动悬架设计PID控制和Fuzzy-PID控制方法,以随机路面作为激励进行仿真,同时对比被动悬架,在相同车况路况下进行仿真实验。结果表明:PID控制和Fuzzy-PID控制均对半主动悬架性能有所改善;Fuzzy-PID控制对悬架性能改善明显优于PID控制,为今后研究汽车悬架提供了参考。
参考文献:
[1] 张俊红,洪刘生,杨文钊,等.车辆悬架系统及其性能评价综述[J].机械设计与研究,2015(6):147-153.
[2] Chen M Z Q,Hu Y,Li C,et al.Semi-active suspension with semi-active inerter and semi-active damper[J].IFAC Proceedings Volumes,2014,47(3):11225-11230.
[3] 宋作军.汽车半主动悬架的非线性动力学分析[J].中国机械工程,2016,27(20):2835-2839.
[4] 夏均忠,马宗坡,白云川,等.路面不平度激励模型研究现状[J].噪声与振动控制,2012(5):1-5.
[5] 杜常清,常晓瑞.PID控制策略下主动悬架系统的动态仿真[J].武汉理工大学学报,2015(6):680-683.
[6] 刘岩.增强学习的PID控制参数优化快速整定算法[J].计算机测量与控制,2014,22(2):467-470.
[7] 李伟平,柳超,张利轩,等.模糊PID控制在磁流变半主动悬架中的应用[J].机械科学与技术,2014,33(12):1708-1713.
