基于改进准静态法的刀盘动应力分析及实测验证*
2018-06-04聂晓东李旋旋霍军周欧阳湘宇
聂晓东,胡 军,李旋旋,霍军周,欧阳湘宇
(1.新疆额尔齐斯河流域开发工程建设管理局,新疆 乌鲁木齐 830000;2.大连理工大学 机械工程学院,辽宁 大连 116024)
0 引言
TBM刀盘在正常掘进情况下所受的载荷为反复循环载荷[1]。反复循环载荷下刀盘本体结构的薄弱环节极易产生疲劳裂纹,在循环载荷作用下会导致裂纹扩展加速,严重时会导致结构失效。盘体动应力的获取是刀盘寿命预测至关重要的一步。刀盘动应力主要依靠现场实测或者利用现场施工参数的计算等方式获得[2],鉴于掘进机的施工条件极端恶劣,不便于传感器的安装,所以依据地质状况和掘进参数等计算对于动应力的获取是方便可行的。
TBM刀盘动应力往往需要依据岩土状况以及掘进数据来计算得到,而模态相加法、振动分析法等均不甚适用于刀盘[3-5],故本文研究了一种改进的准静态法来求解刀盘动应力。
1 改进准静态法步骤
(1) 利用SolidWorks软件构建TBM关键部件模型。
(2) 结合现场施工参数,对整机模型进行ADAMS仿真分析,提取刀盘横向、纵向、轴向的加速度。
(3) 从静力学分析中选取应力值较大的5个节点作为不安全点(危险点)。
(4) 求出加速度和外载作用下刀盘的应力布局。
(5) 根据公式求解动应力子量,合并后获得相关点的动应力:
(1)
其中:σi(t)为i位置的应力时间历程;pk,s为第k种静载荷;pk(t)为与pk,s相同位置处的载荷时程;σi,k为第k种载荷下第i个点的应力;al,s为第l种加速度载荷;al(t)为与al,s相同位置处的加速度时程;σi,l为第l种载荷下第i个点的应力。
2 掘进过程TBM整机动力学仿真
本节对TBM整机进行ADAMS模拟分析,随之通过结果的后处理提取出刀盘加速度。首先用SolidWorks软件构建整机模型;然后分析与等效各部件的运动关系;最终详细分析计算得出加速度结果。
2.1 整机模型的建立
对现有的TBM整机进行测量,然后构建SolidWorks版的整机模型。之后,将新建的模型导入到ADAMS中,导入后的整机模型如图1所示。
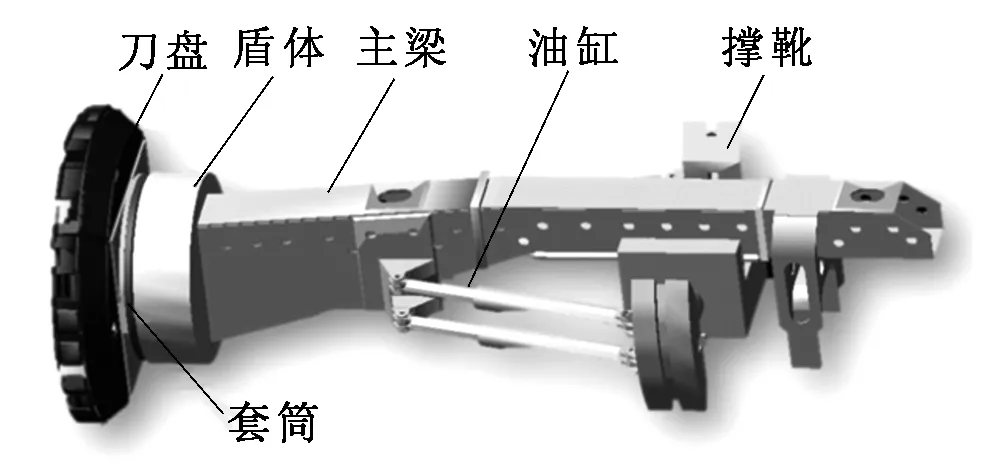
图1 TBM主机模型
2.2 加速度结果分析
以实际施工参数为例,利用ADAMS展开仿真分析,最终获得刀盘系统加速度数据如图2所示。
如图2所示,在0.5 s以前刀盘的横向(X向)、纵向(Y向)、轴向(Z向)加速度振荡较大,在0.5 s后逐渐稳定。因为TBM由静态启动,初始时盘体受到冲击性外载产生了加速度晃动。因盘体质量较大,故轴向的加速度振动规律与其他向不同。
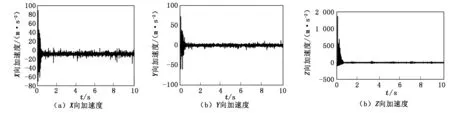
图2 盘体系统加速度分析数据
3 危险点应力时间历程求取
找到TBM盘体的危险点位置,然后利用有限元软件求解单位外载作用下各个不安全点的动应力。根据公式(1)算出不安全点的动应力时间历程。算得的测试点的动应力如图3所示。
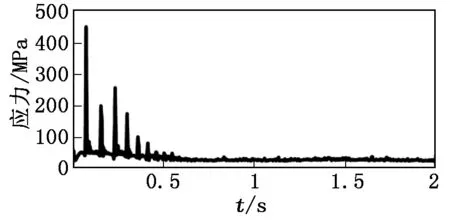
图3 测试点的应力时间历程
4 TBM掘进过程刀盘应力测试
为验证新型准静态法的求解效果,本节利用无线测试装置对某工程TBM盘体应变情况展开测量,随后对测量结果和计算结果做了比较。
4.1 测试方案及测试设备
由于测试环境极端严峻 ,因此测试方案的制定应充分考虑周围环境对仪器的影响。本次试验的测量装备应兼具装卸灵活、数据传送不受周围环境扰动的特点。测量装置主要包括无线网关、应变片、笔记本电脑以及应变传感器等,如图4所示。

图4 无线应变测试系统的构成
4.2 动应力测点确定
TBM刀盘破岩过程中刀盘与岩石的碰撞不可避免,所以传感器安装在盘面上显然是不合适的。同时考虑到刀盘结构中溜碴板、中间面板等的错综布局,传感器的安装位置需谨慎选择。本文考虑将传感器安装到转弯纠偏下应力最大点周边的人孔处。4个应变片用螺栓固定后如图5所示。4个应变计安装在1处,传感器装在2处,天线在3处,装传感器的底座安装在4处浅色区域。
4.3 测试结果分析
一切调试结束后,准备测试。当TBM在下一次掘进快开始时进行测试,采样频率为320次/s。测试数据特征值如表1所示。

图5 传感器和应变片实地安装图

应变片最大值最小值均值方差1587.42206.98372.381 807.42212.45-101.71-46.4501.85
将测试数据转变为应力数据。依据材料力学知识,可知:
(2)
其中:σ1为应变片1方向的应力值;σ2为应变片2方向的应力值;E为弹性模量;μ为泊松比;ε1为应变片1的应变值;ε2为应变片2的应变值。
将盘体材质的弹性模量乘以测试值便可得动应力的数据。图6为现场测试数据与计算值对比。表2为测量点动应力的特征值与计算结果的对比。
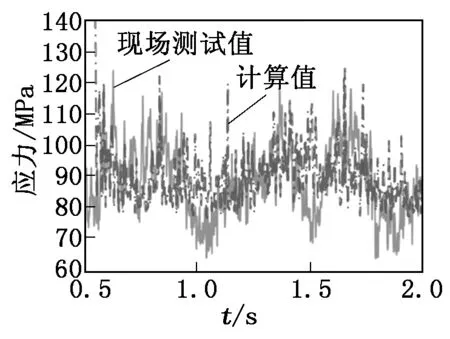
图6 现场测试数据与计算值对比

均值最大值最小值变化范围应力计算值(MPa)91.31141.7076.8764.83应力实测值(MPa)88.48123.7564.7059.05误差(%)3.214.518.89.8
根据表2中计算值和实测值的比对:计算结果的平均值相比实测数据差距较小(3.2%),变化范围相差较大(9.8%)。经分析原因如下:①岩石的单轴抗拉强度低,破岩时滚刀受载小,冲击不明显;②TBM从静止启动,加速度变动大。鉴于一些不确定性的因素,可认为计算结果能够表示TBM刀盘动应力的特征,而研究的最终目的是为了预测刀盘疲劳寿命,较大的应力幅值会使得刀盘寿命预测结果更加保守。所以利用改进的准静态法预判TBM刀盘寿命是可行的。
5 结论
本文研究出一种求解TBM盘体动应力的新型准静态法。首先利用ADAMS仿真分析求出了刀盘的加速度,其次通过危险点的加载得出了危险点的动应力。最后,对某工程TBM应变情况实施了无线测量,经过测量数据和计算数据的比对,得出结论为:均值的误差是3.2%,变化范围的误差是9.8%,最大值的误差是14.5%,最小值的误差是18.8%。
参考文献:
[1] 欧阳湘宇.多点冲击下TBM刀盘裂纹萌生—扩展全寿命预测[D].大连:大连理工大学,2015:15-16.
[2] 凌静秀.空间分布载荷下TBM刀盘振动分析及寿命预测[D].大连:大连理工大学,2015:138-145.
[3] Liu S T.Computational methods for life prediction of mechanical components in dynamic systems[M].Iowa City:The University of Iowa,1986.
[4] 王海霞,汤文成,钟秉林,等.客车车身骨架动应力研究的现状与未来[J].应用力学学报,2001(3):8-13.
[5] 杨扬.基于ANSYS的TBM刀盘动力特性分析[D].天津:河北工业大学,2015:2-6.
