基于跳跃显露模式挖掘算法的癌症分类

乔 媛，廖小平，邵开霞

(河海大学计算机与信息学院，江苏 南京 211100)

0 引 言

当前，随着计算机技术的不断发展和数字网络的普及，各大领域中收集的数据量越来越多，数据库规模也越来越大，如何有效地挖掘这些数据已成为当今研究的重要课题。面对这一课题，人们需要新的技术来整理和分析这些数据集，从而挖掘出有价值的信息，数据挖掘和机器学习由此而生。对于一个分类问题，重点是建立具有泛化能力的学习机或预测模型。传统的方法基本上都是借助各种方法寻找最为精确的预测规则，然而很多情况下，预测模型的精确度会受数据集的多少和数据分布的影响，导致无法寻找分类精确度高的预测模型。但是，产生多个准确度相对较低的粗糙模型还是比较简单的，因此，寻找可以提高已有预测模型准确度的方法显得尤为重要，集成学习便能达到这一目的。集成学习经常使用的是Boosting和Bagging这2种算法，本文主要对这2种算法进行简述，并提出一种适用于挖掘SJEP的改进的Boosting算法。

近年来集成学习在计算机领域得到不断发展，它是用来提高算法的分类精确度的一种方法，被认定为是近年来最高效的提升方法之一。虽然SP-树挖掘出的SJEP具有很好的分类性能，但是它样本覆盖率并不高，得到的结果并不具有一定的泛化性。针对这一问题，本文将通过改进后的Boosting算法来加以改进，提高其分类准确度。对于算法的优化一般从降低时间复杂度或提高算法准确度这2个方面出发，本文以提高算法的准确度为目的对原有算法进行改进，主要改进方法如下：根据Boosting算法的迭代思想，利用这些训练集对基分类器进行迭代。SP-树的优势弥补了集成学习方法的不足，而集成学习又改善了SP-树不具泛化性的缺陷，所以通过集成学习和SP-树的结合，可以提高分类的准确度。

1 相关研究

1.1 分类算法

基于决策树的分类算法[1]，是以树形结构来表示分类结果的方法，树的大小和分类的精确度决定了树的数量，树的根结点代表整个数据集，而每个叶子结点代表一个类，每个内部结点又分别代表一个属性，结点的分支则代表了包含该属性的可能值。该方法首先在训练样本中选择一个子数据集，并利用这些数据集形成一颗决策树，如果该树并不能正确划分所有的对象，那么就将那些例外的对象加入到这棵树中，这样多次反复直至最终得到正确的决策集。

贝叶斯分类是基于贝叶斯理论的一种统计学方法，可以通过概率来预测样本所属的类。基于贝叶斯算法[2]的过程描述如下：假设有C1,C2,…,Ck这K个类，给定未知样本X={x1,x2,…,xn}，分别计算出样本X属于各个类的概率，概率最高的类便是X所属的类，即使P(Ci|X)数值最大的Ci作为X所属的类P(Ci|X)>P(Cj|X),1i,jK,j≠i。

根据贝叶斯定理，P(Ci|X)=P(X|Ci)P(Ci)/P(X)，其中，P(X)对所有类都相等可以看作是一个常数，所以只需P(X|Ci)P(Ci)最大即可。P(Ci)=|Si|/|S|，其中Si是训练集中Ci的样本个数，|S|是训练集中样本的总数。

神经网络[3]的概念最早是由心理学家和神经学家共同提出的，由彼此相连的输入/输出单元组成，其中每一个连接都是和一个权值相连的。神经网络主要是通过对神经网络的权的不断调整，来预测样本的正确类。神经网络需要花费很长的时间，还需要大量的参数，而且这些参数大多都是靠经验来确定的。

关联规则[4]实质上是训练集上频繁出现的项与项之间的一种紧密联系，目前对于频繁项集的挖掘算法中最经典的莫过于Apriori算法。Apriori算法的基本思想是：先扫描一遍数据库，统计出每个项的计数，选出那些支持度大于等于最小支持度阈值的项，找到频繁1-项集合S1，然后利用S1找出所有的频繁2-项集合S2，接着用S2找到S3，顺序进行下去，直到不能再找到k-项集为止。因为找到每个Sk都需要扫描一遍数据库，所以挖掘效率非常低，一般应用中不太推荐使用。

1.2 显露模式

EP[5](显露模式)是一种新的知识模式，它是从一个数据集到另一个数据集支持度发生显著变化的项集，体现了2组不同数据集之间的多组属性差异，具有良好的分类性能，目前已被广泛应用于分类中。JEP(跳跃显露模式)是近年来基于EP提出的一种新模式，可以比较明确地显示出2个数据集之间存在的差异。据研究显示，基于跳跃显露模式的分类算法在数据量和维数上具备可规模性，而且还具备良好的预测准确性。

设数据集是包含N个实例的标准关系表，而每个实例都有n个属性，所有的属性已经离散化并映射到区间值。假设这些数据被划分为C1,C2,…,Ck这样的k个已知类,每个训练数据都有其所属的类别。I={i1,i2,…,in}是出现在样本中的项的全集，其中子集X⊆I称为项集。其实，每个样本都是一个包含n个元素的项集，而训练集就是由若干个项集组合而成。

定义1支持度(Support，sup)：数据集D中包含项集X的个数记为countD(X)，数据集D中的样本总数记为|D|，项集X在数据集D中的支持度记为supD(X)，supD(X)的计算公式如下：

定义2增长率(GrowthRate,GR):对于2个数据集D1和D2，项集X从D1到D2的增长率GR(X,D1,D2)的计算公式如下：

定义3显露模式(Emerging Patterns，EP)：如果一个项集X从D1到D2增长率GR(X,D1,D2)≥ρ，ρ为增长阈值，则称X为从D1到D2的显露模式EP[6]。

1.3 集成学习

集成学习是目前机器学习领域中的一种新的学习范式，也是发展最快的分支之一，它的主要思想是通过对简单的学习算法的调用来构造出更多的基分类器，然后评估各个基分类器的分类性能，利用某种策略将这些基分类器组合成最终的集成分类器，从而提高分类的性能。近年来，集成学习算法逐渐受到广大学者的关注，Zhang等人[7-8]利用TDNN时延神经网络成功将集成学习应用于语音识别中，利用改进的局部Boosting算法对基因数据进行分析。Breiman[9]于1990年提出了Bagging算法，也叫自举汇聚法，是随机抽样、迭代、独立学习的过程，是一种基于训练集构造分类器的最简单直观的方法[10]。张翔等人[11]采用基于Bagging改进后的Attribute Bagging算法实现了对中文文本的分类。集成学习主要包括提升(Boosting)和装袋(Bagging)这2种算法[12]，虽然这2种算法使用的方法不大相同，但是它们也存在相同之处，即两者都是将许多基分类器合并起来得到最终有效的分类器，从而提高分类的精确度。

Bagging方法的基本思想：先给定一个弱分类器，有放回地对训练数据集随机抽样，组成大小相同但是其样本不同的多个训练集，接着利用这些训练集让弱分类器迭代T次，每次迭代完都得到一个基分类器f1,f2,…,ft。最后用这些分类器对样本进行预测，并根据结果对分类器进行投票，根据投票权重大小得到最终的集成分类器。实现过程如图1所示。

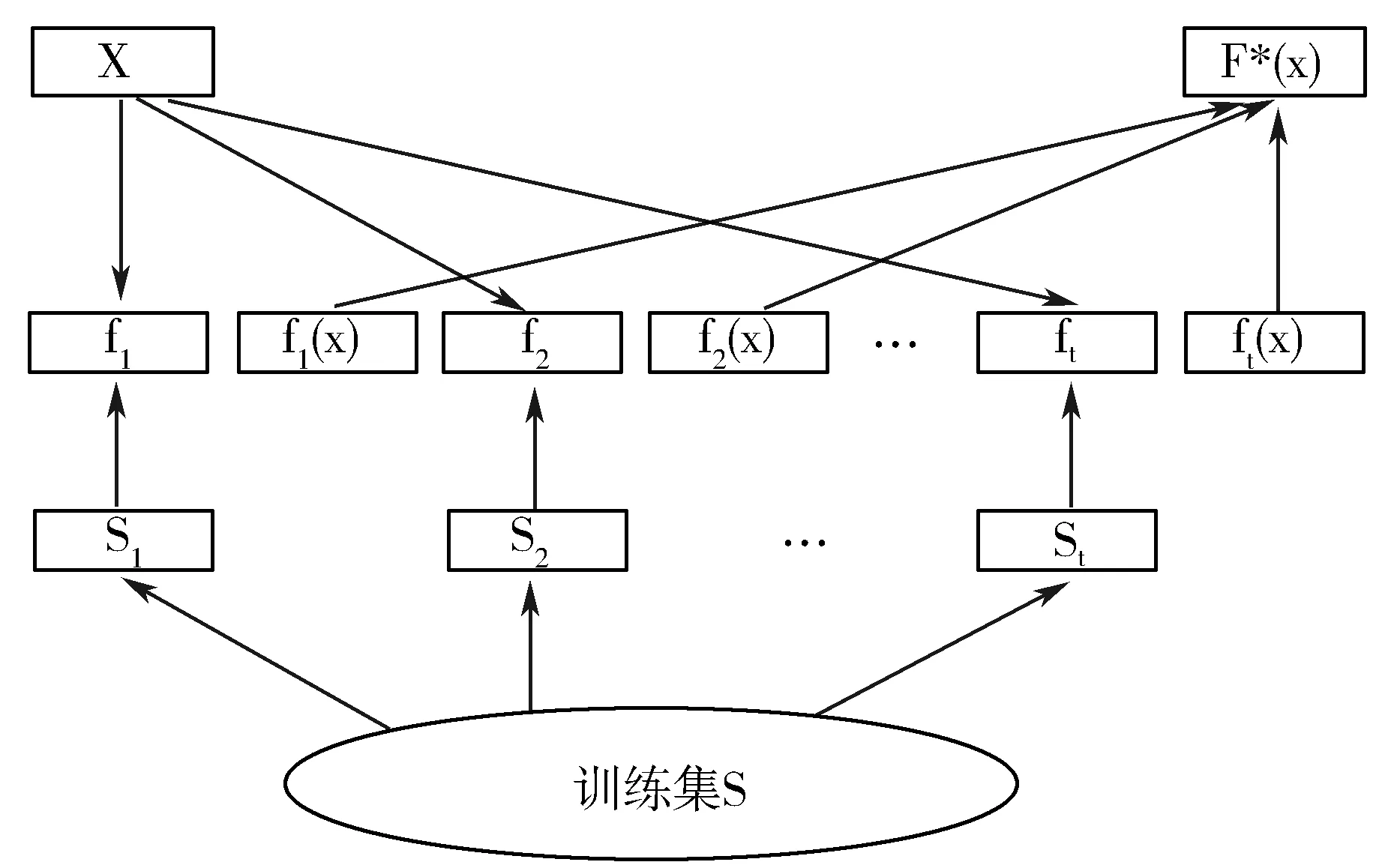
图1 Bagging算法实现过程

Bagging算法利用对训练集的重新选择来增强分类器的丰富性，进而使其泛化能力得以提高。但是这种集成分类器的效果并不一定比单个分类器要好，其分类性能决定因素在于基分类器构造的稳定性。对数据集做微小的变动，假如说基分类器的准确度并没有多大的变化，那么经过Bagging集成后的算法的分类效果与单分类器差不多；如果单个基分类器的准确度变化很大，那么集成后的算法分类的效果要比单个分类器要好很多。

Boosting算法是一种旨在提升给定算法的普通方法，它是从Valiant[13]提出的PAC(概率近似正确)学习模型中得到的灵感，PAC是机器学习的基本理论。Valiant当时提出了这样一个问题：一个性能较好的“弱”学习算法是否可能被“提升”为“强”的学习算法？随后，1990年Schapire[14]便提出了第一个多项式时间算法——Boosting算法，对这个问题作出了回答。之后，Freund[15]设计了一个更加高效的Boost-by-majority算法，该算法通过重取样或过滤的方法对Boosting算法加以改进，虽然这种算法在某种意义上是对原来的算法有所改进，但是在实际应用中仍然存在着一些缺陷。Freund也发现了这些缺陷，于1995年与Schapire一起提出了AdaBoost[16]算法，这种算法虽然与之前的Boost-by-majority算法效率一样，但是它很容易被运用到实际应用中。

与其他算法相比，Boosting算法具有不少优点，比如它运算速度快、算法简单、容易编程等，不需要事先对弱分类器加以处理，只需要给出足够多的数据，通过数据找出比之前的弱分类器更好的分类器，就能得到最终的强分类器；只要有充足的数据信息，就能使分类器达到实验所想要的分类精确度；从理论上而言，Boosting算法能与任意的弱分类算法进行集成学习，生成适应性较强、分类精确度较高的新算法[17]。

2 Boosting分类算法的改进

2.1 基本思想

本节首先对Boosting算法提出一些改进措施，对于Boosting算法的提升过程往往是针对于特定问题进行的应用改进，这就依赖于单个弱分类器的分类性能，并且实验过程中需要大量具体的数据。但是对于有限的数据而言，人们更加希望它能最大程度地挖掘这些数据中有价值的信息，这就需要对Boosting算法中的细节作一些调整。

在改进过程中，采取以下优化措施：1)通过对Boosting算法中误差权值的改进，避免算法过早地停止，使Boosting算法精确度更高；2)通过对抽样权重引入参数，降低更新后抽样权重的值，使算法更加精确；3)引入相似度的概念，改进Boosting算法的抽样权重，使算法更加精确。

2.2 改进的Boosting算法

本文就如下几点做出改进：

1)在训练集L1中测试弱分类器f1(x)，计算它的权重误差ε1。一般情况下，当某分类器的εm>0.5或εm=0时，算法便会停止，而本节中构造的基分类器可能已经具备较高的分类准确率，从而使误差εm=0。在这里为了限制算法过早地停止，Bauer和Kohav建议当εm=0时，令εm=10-10继续进行后面的操作，这样就相当于给该分类器无限大的投票权重。

2)引入参数β来降低正确或错误的分类个体抽样权重改变的量，从而使算法更加精确。

3)利用集成学习的思想，为最终生成的强分类器中的各弱分类器权重引入相似度系数，进一步精确弱分类器的权重值，以此提高强分类器的分类精确度。

本文根据以上几点内容提出一种改进的Boosting算法，在迭代过程中计算出每个弱分类器的权重训练误差率，然后利用该误差率更新其投票权重。改进的Boosting算法描述如下：

初始化：F0(X)=0，每个样本的抽样权重为w1(xi)=1。

算法步骤:

3)如果εm>0.5,则令M=m-1，退出循环；如果εm=0，则令εm=10-10，继续进行循环；

5)更新抽样权重：

输出：

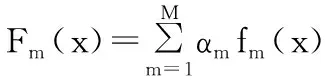
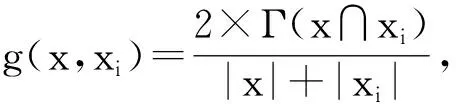
在上述改进的Boosting算法中，参数β降低了算法中赋予各分类个体的权重的变化量，使得算法可以对更多的数据信息进行分析，从而使算法的预测更加精确。但是对于引入参数β，我们并不知道其取值多少才合适，所以需要对参数β的取值进行研究。为了更好地对改进前后的算法进行比较，需要排除其他影响因素，比如随机抽样的个数n，需要对其取值的大小进行研究，找出合适的取值。

3 SP_Boost算法

3.1 基本思想

本文将SP-树分类算法和改进的Boosting算法相结合产生的新算法记作SP_Boost分类算法。SP_Boost分类算法实际上是在SP-树分类算法的基础上，通过集成学习得到的新算法的简称。通过Boosting算法的迭代后得到的SP_Boost分类算法，在理论上可以提高SP-树算法的分类准确率。SP_Boost分类算法的实际过程如图2所示。

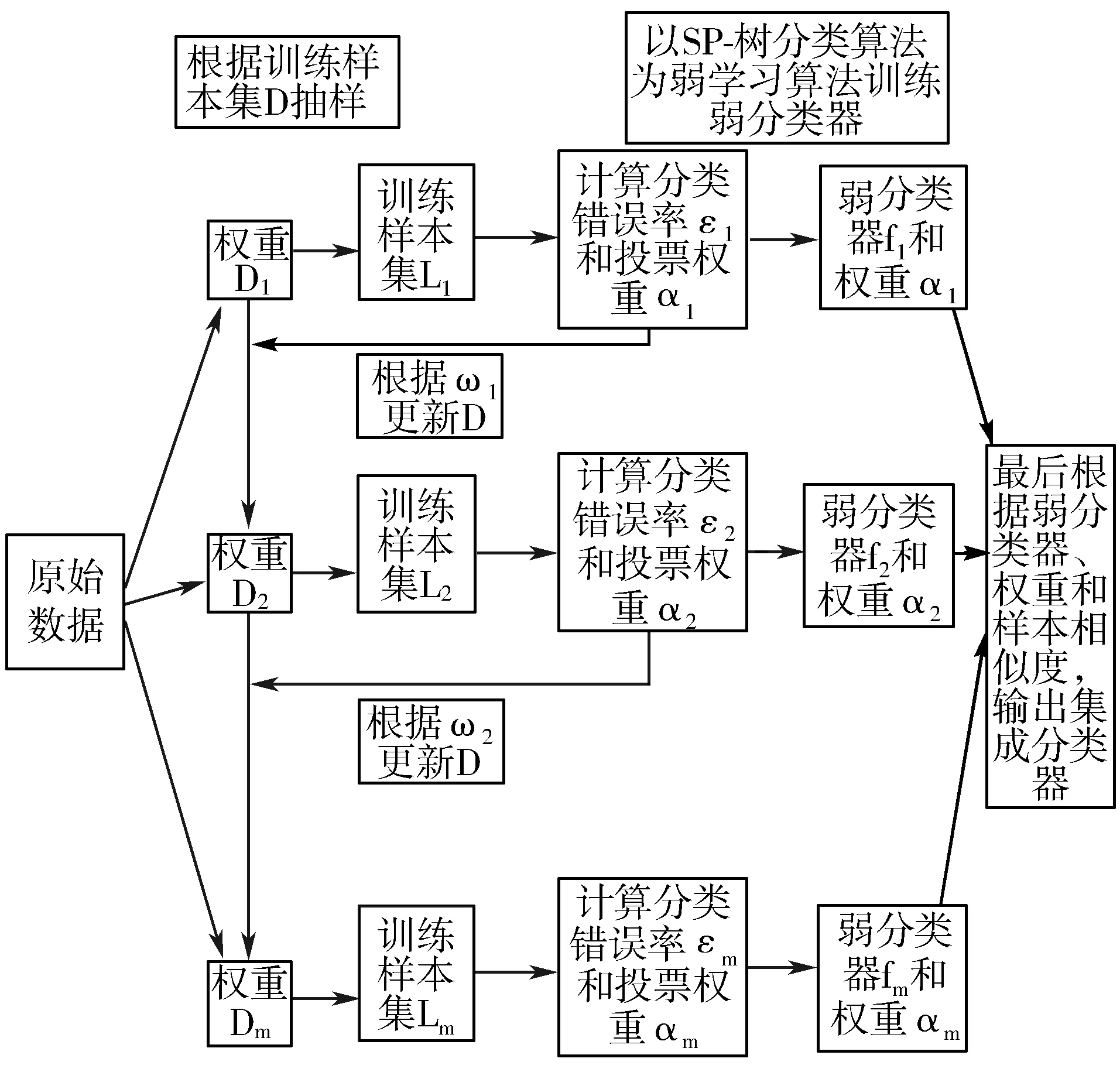
图2 SP_Boost分类算法实际过程

3.2 SP_Boost算法

该算法的主要过程如下：利用SP-树分类算法作为基学习算法，训练样本集构造基分类器f1(x)，并将这个基分类器作为改进后Boosting算法的第一个基分类器，以此提高整体分类的精确度。具体步骤如下：

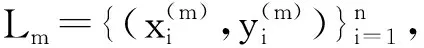
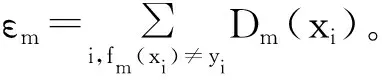
4 实验分析

4.1 数据介绍

本文实验选用UCI中的Breast Cancer数据集、国内Broad Institute数据库中的Leukemia和Lung Cancer数据集进行实验，如表1所示。其中，Breast Cancer数据集中包含699个样本，每个样本包含10个属性；Leukemia数据集中一共包含15063个样本，每个样本中包含30个属性； Lung Cancer数据集中一共有6317个样本，每个样本包含58个属性。而每个数据集中均包括2个类：癌症数据和不是癌症数据。对于每个样本集，抽取2/3样本为训练样本，剩余样本为测试样本。

表1 实验数据集

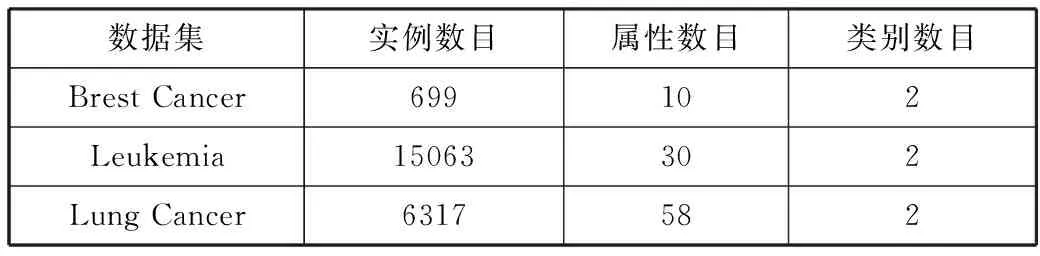
数据集实例数目属性数目类别数目Brest Cancer699102Leukemia15063302Lung Cancer6317582

本次实验中的数据属性选择已经排除了用户姓名等无关信息。其中，Brest Cancer数据集中主要包括癌细胞的大小、有无肿块、是否有过手术、是否有遗传史、是否有孕等信息。而Lung Cancer数据集中并不包含是否有孕、是否手术、是否有过手术的信息，其他信息均包含，除此之外主要包括9项血清蛋白各项指标、23项癌细胞化验各项指标结果、13项血检各项指标等信息。Leukemia数据集中比Lung Cancer数据集少了几项癌细胞的指标，主要是癌细胞种类不同，所以检查指标有所差异。这些指标数据通常可被划分为10级，为了试验的方便，根据不同指标对应等级修改后存入数据库表中，比如AD.201t指标修改为AD.201t1、AD.201t2、…、AD.201t10，其他指标也是按照该标准划分。

4.2 改进前后的算法性能对比

实验对SP_Boost算法、改进前的Boosting算法和SP-树算法的分类性能进行分析对比。本文实验中采用Holdout[18]验证，来对改进前后的算法分类精确度进行比较。实验分别在不同的支持度阈值下，对SP-树分类算法、改进前的Boosting算法和SP_Boost分类算法的分类精确度和运行时间进行了比较。实验首先从每个样本集中抽取2/3样本为训练样本，剩余样本为测试样本，然后根据训练样本训练出分类器，再用测试样本对分类器的分类准确度进行分析。

1)在Breast Cancer数据集上运行结果比较。

对于Breast Cancer数据集，分别对5种不同的最小支持度阈值下的实验结果对比分析，其中准确度及运行时间(×102s)均为平均值，如图3所示。

图3 Breast Cancer数据集上的准确度对比

2)在Leukemia数据集上运行结果比较。

对于Leukemia数据集，分别对6种不同的最小支持度阈值下的实验结果对比分析，其中准确度及运行时间(×102s)均为平均值，如图4所示。

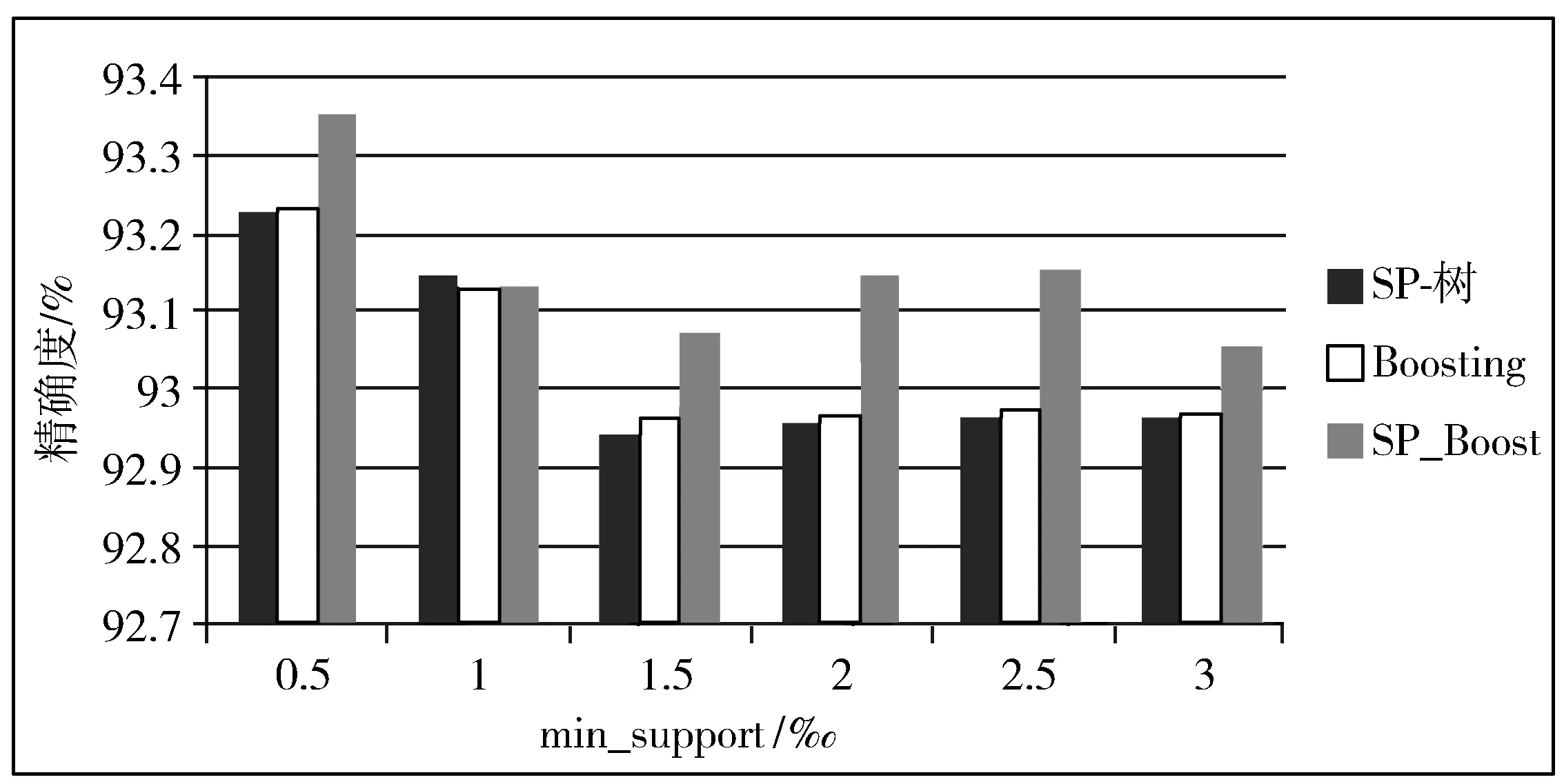
图4 Leukemia数据集上的准确度对比

3)在Lung Cancer数据集上运行结果比较。

对于Lung Cancer数据集，分别对5种不同的最小支持度阈值下的实验结果对比分析，其中准确度及运行时间(×102s)均为平均值，如图5所示。

图5 Lung Cancer数据集上的准确度对比

4.3 实验结果分析

从图3～图5中还能发现，最小支持度阈值对分类准确度有一些影响，但是影响相对较小。当最小支持度阈值增大时，由于过滤掉的数据变多，可能过滤掉了一些有用的数据，使得分类的准确度有所下降。但是本文中支持度阈值的变化量并不大，对于支持度阈值的增加而过滤掉的数据量并不是很大，所以影响相对较小，但是并不能保证支持度阈值继续增加时，对分类准确度的影响会变得比较明显。由此看来，在实验前选定合适的最小支持度阈值，减少对结果的影响是比较重要的。

5 结束语

本文共提出2个改进点，即对Boosting算法的改进和基于改进的Boosting算法对SP-树的改进(SP_Boost)。首先，对改进的Boosting算法进行分析，可见改进后的算法中引入了参数和权值系数，很明显增加了原有算法的时间复杂度。但是它引入了参数和相似性系数，在降低了各分类个体的权重的变化量的同时，还增大了与待测样本相似性较高的样本的权重，从理论上而言，这些改进方法可以使算法的结果更加精确，提高算法的分类准确率。

然后，对改进的SP_Boost算法进行分析，其基本原理是以SP-树分类算法作为弱学习算法，利用Boosting迭代的思想对其迭代M次，这个过程产生的时间复杂度是原来的M倍，所以从时间复杂度上进行分析，改进后的算法并没有得以改善，但是从理论上而言，经过迭代后的算法，提高了原始算法的分类精确度。综上所述，本文的2点改进都在一定程度上提高了原有算法的分类准确率。

参考文献：

[1] Garcia-Almanza A L, Tsang E P K. Simplifying decision trees learned by genetic programming[C]// IEEE Congress on Evolutionary Computation. 2006:2142-2148.

[2] Domingos P. Beyond independence : Conditions for the optimality of the simple Bayesian classifier[J]. Machine Learning, 1996,29:105-112.

[3] Russell S, Binder J, Koller D, et al. Local learning in probabilistic networks with hidden variables[C]// International Joint Conference on Artificial Intelligence. 1995:1146-1152.

[4] Lent B, Swami A N, Widom J. Clustering association rules[C]// Proceedings of IEEE International Conference on Data Engineering. 1997:220-231.

[5] Dong Guozhu, Li Jinyan. Efficient mining of emerging patterns: Discovering trends and differences[C]// Proceedings of ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. 1999:43-52.

[6] Li Jinyan, Dong Guozhu, Ramamohanarao K. Making use of the most expressive jumping emerging patterns for classification[J]. Knowledge & Information Systems, 2001,3(2):131-145.

[7] Zhang Chun-xia, Zhang Jiang-she. RotBoost: A technique for combining Rotation Forest and AdaBoost[J]. Pattern Recognition Letters, 2008,29(10):1524-1536

[8] Zhang Chun-xia, Zhang Jiang-she, Zhang Gai-ying. Using Boosting to prune Double-Bagging ensembles[J]. Computational Statistics & Data Analysis, 2009,53(4):1218-1231.

[9] Breiman L. Bagging predictors[J]. Machine Learning, 1996,24(2):123-140.

[10] 郭照斌. Bagging算法神经网络的抗噪声能力及应用[D]. 大连：大连理工大学, 2009.

[11] 张翔,周明全,耿国华,等. Bagging算法在中文文本分类中的应用[J]. 计算机工程与应用, 2009,45(5):135-137.

[12] Bauer E, Kohavi R. An empirical comparison of voting classification algorithms: Bagging, Boosting, and Variants[J]. Machine Learning, 1999,36(1-2):105-139.

[13] Valiant L G. A theory of the learnable[J]. Communications of ACM, 1984,27(11):1134-1142.

[14] Schapire R E. The strength of weak learnability[J]. Machine Learning, 1990,5(2)：197-227.

[15] Freund Y. Boosting a weak learning algorithm by majority[J]. Information & Computation, 1995,121(2):256-285.

[16] Freund Y, Schapire R E. A decision-theoretic generalization of on-line learning and an application to Boosting[J]. Journal of Computer & System Sciences, 1997,55(1):119-139.

[17] 刘凯,王正群. 一种用于分类的改进Boosting算法[J]. 计算机工程与应用, 2012,48(6):146-150.

[18] Dwork C, Feldman V, Hardt M, et al. Generalization in adaptive data analysis and holdout reuse[C]// International Conference on Neural Information Processing Systems. 2015:2350-2358.