巷道围岩加固体力学特性与稳定性分析*
2018-06-04谷拴成黄荣宾
谷拴成,周 攀,黄荣宾
(西安科技大学 建筑与土木工程学院,陕西 西安 710054)
0 引言
随着浅部煤炭资源日趋枯竭,煤炭开采逐渐走向深部开采阶段,与浅部巷道相比,深部巷道围岩力学环境更加复杂,深部高应力巷道围岩呈现出非连续性、非协调性大变形、大范围失稳破坏等一系列工程响应问题[1-6]。近年来,锚杆支护技术已成为煤矿巷道首选的主要支护方式,我国国有大中型矿井的锚杆支护率达到60%以上,有些矿区甚至达到100%,使得锚杆支护技术得到了快速发展[7]。深部煤炭开采使得矿井发生重大安全事故的危险性增加,严重威胁矿井安全生产。
深部高应力、大断面和软岩巷道的围岩稳定性控制一直是矿井开采的主要技术瓶颈之一,国内外许多专家、学者对此做了大量的理论研究、实验与数值模拟,取得了丰富的成果。何满潮等[8]采用现场工程调查、微观组构实验等手段,分析了巷道围岩破坏失稳主要是由于支护体与围岩在力学特性上的不耦合造成的;肖同强等[9]采用相似模型试验方法,分析了埋深、构造应力等因素对厚顶煤巷道围岩变形、围岩应力及支护结构的影响,揭示了厚顶煤巷道围岩稳定性规律;徐立功等[10]结合强度折减法对隧道开挖过程中围岩稳定性进行数值分析,研究了随着折减系数的变化,隧道围岩塑性区的变化情况;李宁等[11]通过数值模拟试验的方法,建立了能够考虑初期支护安全性的围岩稳定评价新方法;侯朝炯等[12]研究了锚杆支护对锚固范围岩体峰值强度和残余强度的强化作用,分析了锚固体强度强化后对围岩塑性区和破碎区的控制程度;戴怡文等[13]采用Q系统分级法、RMR岩体分类和BQ分级法对矿区岩体进行质量评价,结合块体理论和三维有限元分析进路开挖后顶板的稳定性;Pan和Dias采用运动学方法结合强度折减技术来评估加固隧道工作面的安全系数[14];Anagnostou和Perazzelli基于极限平衡法,提出了一种计算方法来评估锚杆加固下的粘性摩擦土中隧道表面的稳定性[15]。
上述学者们提出了不同研究思路,促进了地下工程迅速发展,然而,围岩稳定性分析还没有形成统一的理论,大多数停留在定性的或经验的水平,缺乏定量的围岩稳定性分析。因此,本文在前人的基础上,将锚杆与围岩的复合体考虑成一种新的支护结构,将其定义为围岩加固体,并且求出了围岩加固体的弹性模量、泊松比、黏聚力和内摩擦角的表达式,在此基础上建立了围岩与加固体协调变形力学模型,用加固体变形程度来判断围岩稳定性,并定义了围岩稳定性系数,最终提出了围岩稳定性的定量评价方法。
1 围岩加固体定义与力学模型建立
1.1 定义围岩加固体
为了增加围岩的整体性和强度以及达到支护围岩的目的,坑道、隧道、硐室、矿井、巷道、采石场等工程常常使用锚杆作为一种支撑形式。在地下硐室中,为了确定合理的锚杆支护参数与评价被锚岩体的稳定性,采用均匀化方法,从宏观上将岩体和锚杆的复合体考虑成材质连续、均质、各向同性的围岩加固体,将加固体看作为一种新的支护结构,约束深部围岩变形,如图1所示。加固体有着与岩体相同的物理性质,比如容重、比重、空隙率、吸水率等,相比围岩物理力学参数而言,锚杆的支护作用使得加固体的变形参数与强度参数得到了改善。

图1 围岩加固体示意Fig.1 The surrounding rock reinforcement body schematic
1.2 建立力学分析模型
巷道开挖后,围岩应力重分布使得围岩向巷道内部挤压变形,通常会适时向围岩打入锚杆,起到约束围岩变形的作用,将锚杆锚固区域等效为围岩加固体后,锚杆支护围岩就转化成了加固体约束被锚岩体之外的围岩变形,同时加固体在围岩压力的作用下也会产生变形,因此,建立了围岩与加固体协调变形力学模型,如图2所示。Es,μs为围岩的弹性模量与泊松比;Cs,φs为围岩内聚力与内摩擦角;E,μ为加固体的弹性模量与泊松比;C,φ为加固体的黏聚力与内摩擦角;P为原岩应力;R0为巷道半径;h为加固体厚度,其值等于锚杆长度L;Rq为加固体塑性区半径;R1为加固体外缘半径,且R1=R0+L。
在分析模型时做如下假设:
①原岩应力为各向等压状态(λ=1),围岩与加固体均为连续、均质、各向同性的弹性体。
②锚杆与围岩紧密联接,互补解耦,锚杆沿着洞壁均匀布置,且锚杆作用的影响范围为相邻两锚杆间距的一半。
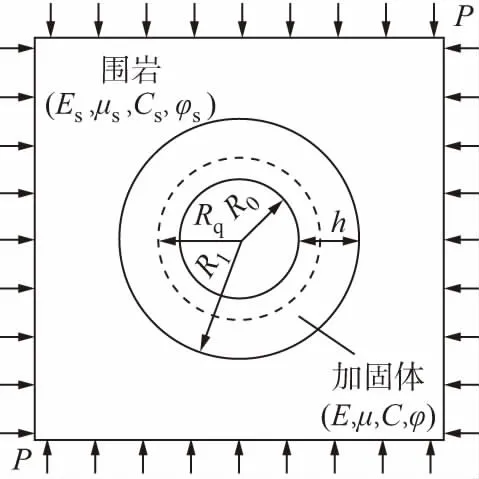
图2 力学分析模型Fig.2 Mechanics analysis model
2 围岩加固体物理力学参数确定
2.1 求解加固体变形参数E,μ表达式
为了求得加固体变形参数,首先将锚杆对围岩的支护作用转化为一组夹紧力,作用于锚杆两端点处围岩,如图3所示,对在夹紧力作用下的围岩进行弹性分析,求得锚杆两端点处围岩的径向位移。

图3 锚杆作用下围岩变形Fig.3 Deformation of surrounding rock under the action of bolt
继而,在与前者相同的原岩应力下,对围岩与加固体协调变形力学模型进行弹性分析,如图4所示,求得加固体内外边缘的径向位移,根据两者引起围岩的变形相同建立等效条件(锚杆两端点处围岩径向位移相等),即可推导出加固体的变形参数。

图4 加固体作用下围岩变形Fig.4 Deformation of surrounding rock under the action of the reinforcement body
2.1.1 锚杆作用下围岩变形
锚杆轴力由预紧力和围岩变形引起,锚杆轴力分布为:
(1)
式中:P1为锚杆预紧力,kN;Δl锚杆伸长量;L为锚杆长度,m;A为单根锚杆横截面积,m2;Eb为锚杆弹性模量,GPa。
将锚杆的支护作用等效为一组应力p,q,则:
(2)
式中:Sl为锚杆排距,m;Sr为锚杆间距,m。
围岩应力与位移表达式为:
(3)
式中:i=1表示锚固体,i=2表示锚固体外的围岩。
边界条件:在r=R0处,σr1=-p;在r=R1处,σr2=σr1+q,ur1=ur2;在r→∞处,σr2=-P。
将边界条件带入式(3)求得Ai,Ci,即可得到锚杆两端点处围岩位移为:
(4)
锚杆伸长量可表示为:
Δl=ur1(R1)-ur1(R0)
(5)
2.1.2 加固体作用下围岩变形
(6)
式中:j=3表示加固体,j=4表示加固体外的围岩;E3=E,μ3=μ,E4=Es,μ4=μs。
边界条件:在r=R0处,σr3=0;在r=R2处,σr3=σr4,ur3=ur4;在r→∞处,σr4=-P。
将边界条件代入式(6)可解的Aj,Cj,即可求得锚杆两端点处围岩的位移:


(7)
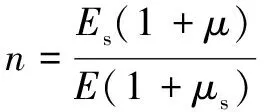
(8)
(9)
当围岩中未施加锚杆,即Eb=0或db=0,带入前面推导可得p=0,q=0,将p,q带入式(8)、(9)可得E=Es,μ=μs。
2.2 求解加固体强度参数C,φ表达式
加固体的内摩擦角由锚杆的内摩擦角、岩土体内摩擦角和摩擦面上的应力状态决定,已有研究表明,加固体的内摩擦角与锚固前土体的内摩擦角相比变化很小[16-17],即:
φ=φs
(10)
锚固岩体的最大主应力方向与锚杆垂直,则锚固体主破裂面方向与最大主应力方向的夹角为:
在围岩锚固区内锚杆与围岩协调变形,锚杆通过轴向受力改善了围岩应力状态,同时也提高了围岩内聚力[18],则加固体内聚力为:
(11)
当围岩中未施加锚杆,即Eb=0或db=0,带入前面推导可得锚杆轴力F=0,将F带入式(11)可得C=Cs。
3 模型求解与围岩稳定评价
3.1 求解模型
对图2力学模型进行弹塑性分析,由平衡方程和屈服条件可得加固体塑性区应力分量为:
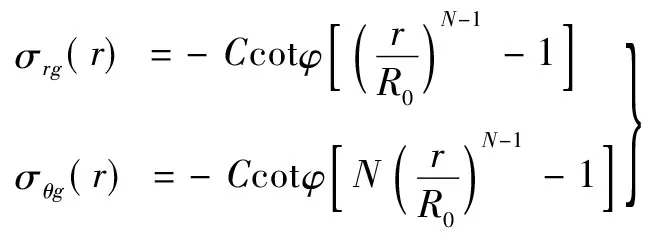
(12)
式中:N为加固体塑性系数,且:
对围岩和加固体弹性区建立平衡方程、几何方程和物理方程可解得围岩与加固体弹性区应力分量为:
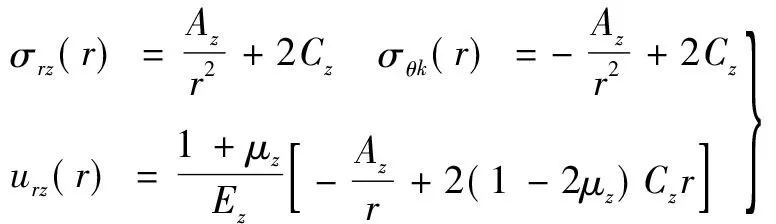
(13)
式中:z=5表示在该模型加固体外的围岩,z=6表示加固体弹性范围;E5=Es,μ5=μs,E6=E,μ6=μ。
围岩与加固体协调变形模型的边界条件为:
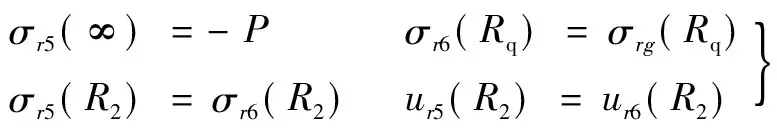
(14)
在加固体弹性区内,当r=Rq时,材料刚进入屈服状态,应力分量应满足M-C屈服条件,即:
(15)
由式(12)、(13)、(14)和(15)可求出Az,Cz,即可解得Rq与围岩、锚杆参数之间的关系表达式。
(16)
由前面推导可知,当围岩中未施加锚杆时,可得到加固体物理力学参数与围岩物理力学参数相等,即E=Es,μ=μs,φ=φs,C=Cs,将围岩与加固体物理力学参数带入式(16)解得Rq为:
式中:Rp为未支护锚杆时修正的芬纳公式表达的围岩塑性区半径。
3.2 围岩稳定评价方法
经过前面推导可知,首先要保证巷道洞壁位移不大于巷道允许出现的最大位移,不影响巷道正常使用,其次必须保证锚杆未失效,若锚杆失效,加固体承载结构则不能形成,最后必须保证加固体承载结构未完全屈服,即使部分屈服仍然能够约束深部围岩变形,控制围岩稳定。用加固体的变形程度来判断锚杆支护效果以及围岩稳定性,能够优化锚杆参数,避免锚杆支护不足或支护过剩。
(1)巷道洞壁位移
假设塑性区体积不可压缩,仅仅形状改变,则巷道洞壁位移为:
u0=Rqur6(Rq)/R0≤[u]
(17)
式中:[u]为巷道洞壁允许的最大位移。
(2)锚杆轴力
(18)
式中:[F]为锚杆允许的最大拉力。
(3)定义围岩稳定性系数
当原岩应力很小或者锚杆支护强度很高时,加固体全部处于弹性状态,表明围岩稳定性好,当原岩应力很大或者锚杆支护强度很低时,加固体全部处于塑性状态,表明围岩稳定性差,围岩即将或者已经失稳,因此,在特定的原岩应力下,合理的锚杆支护会使得加固体部分屈服,但仍能够约束深部围岩变形,较好地控制围岩稳定性,因此,围岩稳定系数k表示在原岩应力P作用下加固体弹性区范围在整个加固体中所占比例。当k=0,则加固体全部处于塑性状态,围岩稳定性很差;当0 (19) 某巷道的开挖断面为拱形,其截面尺寸为5.4 m×4.27 m,按巷道最大半圆计算偏于安全,则等效圆半径为R0=2.74 m,岩体的弹性模量Es=2.1×103MPa,围岩泊松比μs=0.3,围岩内聚力Cs=0.6 MPa,围岩内摩擦角φs=31°,原岩应力P=4.5 MPa。对该巷道进行锚杆支护设计,锚杆支护参数如表1所示。 表1 锚杆支护参数Table 1 Bolt support parameters 将围岩与锚杆参数带入第2章推导公式中可解得围岩加固体物理力学参数,如表2所示。计算过程如下: 将围岩参数与锚杆参数带入式(1)~(5)可得到关于锚杆伸长量Δl的方程式,可解得: Δl=8.254×10-4m 将Δl带入式(1)、(2)得到锚杆轴力F、作用于洞壁的压力p和作用于锚杆远端处围岩的压力q,即: F=72.689 kN,p=89.739 kN,q=47.838 kN 将F,p和q带入式(8)~(11)可解得围岩加固体变形参数与强度参数,即: 2.187 GPa 表2 物理参数对比Table 2 Comparison of physical parameters 由表2可看出,与围岩参数相比,加固体弹性模量和内聚力分别增加了4.12%和5.7%,加固体泊松比减少了1.40%,可知,锚杆支护对围岩加固体内聚力影响最大。 将围岩、锚杆和加固体参数带入式(16)可解得Rq=4.26 m,由式(17)、(18)可解得巷道洞壁位移u0=19.10 mm,F=245.38 kN<[F]=350 kN,由式(19)可求得k=0.365,可以看出依照传统支护理论设计的锚杆支护参数能较好保证围岩稳定,但锚杆强度未完全发挥,因此调整锚杆间排距为1.2 m×1.2 m,同时增加锚杆预紧力到100 kN,则在新的支护方案下,锚杆轴力F=296.06 kN<[F]=350 kN,巷道洞壁位移u0=19.08 mm,围岩稳定系数k=0.367。 将调整锚杆支护前后的理论计算值与实测值进行分析来验证本文理论的合理性,如表3所示。 由表3可知,在方案1,2支护下,理论计算得到的洞壁位移与实测值分别相差1.43 mm和1.27 mm,理论计算得到的锚杆轴力与实测锚杆轴力分别相差4.16 kN和3.33 kN,从而验证了围岩加固体理论的合理性。对比分析可知,在新的支护方案下,不仅保证了巷道围岩稳定性,而且有效发挥了锚杆承载能力,节约了锚杆用量,还能实现锚杆支护参数优化。 表3 支护效果分析Table 3 Analysis of bolt support effect 下面结合算例,分析不同锚杆支护强度对巷道洞壁位移以及塑性区范围的影响,计算选用MATLAB软件。 1)锚杆长度、间排距组合影响规律 其他支护条件不变,仅仅改变锚杆长度与间排距来分析围岩稳定性系数k的变化,如图5所示。 图5 锚杆长度、间排距对围岩稳定性的影响Fig.5 Influence of bolt length and spacing on stability of surrounding rock 由图5可以看出,围岩稳定性随着锚杆长度增加而提高,但随着锚杆长度增大,围岩稳定系数k的增幅在减小,当锚杆长度小于1.5 m时,围岩稳定系数k=0,表明支护强度不够,加固体全部屈服,围岩稳定性很差,当锚杆长度由1.5 m增大到4.2 m时,围岩稳定系数k提高了0.623;围岩稳定系数k随着锚杆间排距增加而减小,但随着锚杆间排距增大,围岩稳定系数k的变化幅度也在减小,当锚杆间排距由0.6 m×0.6 m增大到1.2 m×1.2 m时,围岩稳定系数k减小了0.055;还可以看出,当锚杆设计长度较短时,要保持围岩稳定性不降低,可以较密布置锚杆。因此,锚杆支护设计时应遵循长而疏、短而密的原则。 2)锚杆预紧力影响规律 其他支护参数不变,只改变锚杆所受到的预紧力大小来分析预紧力对围岩稳定性的影响,如图6所示。 图6 锚杆预紧力对围岩稳定性的影响Fig.6 Influence of bolt preload on stability of surrounding rock 由图6可以看出,围岩稳定系数k随着锚杆预紧力增加而增大,锚杆预紧力与围岩稳定系数k成线性变化,当预紧力增大到175.4 kN时,锚杆轴力F=[F]=350 kN,如果预紧力继续增大,锚杆失效,围岩稳定性系数k与未施加锚杆时相等,此时k=0.329。当锚杆预紧力由0增加到175.4 kN时,围岩稳定系数k增加了0.077。 3)锚杆弹性模量与直径影响规律 锚杆弹性模量与直径对围岩稳定性的影响,如图7所示。 图7 锚杆弹性模量、直径对围岩稳定性的影响Fig.7 Influence of the elastic modulus and diameter of the bolt on the stability of surrounding rock 由图7可以看出,围岩稳定系数随着锚杆直径增大而增大,随着锚杆直径越大,k值的增幅越大,当锚杆直径由16 mm增大到25 mm时,围岩稳定系数k增加了0.01;围岩稳定系数随着锚杆弹性模量增加而匀速增加,当锚杆弹性模量由190 GPa增大到210 GPa时,围岩稳定系数k增加了0.001。因此,锚杆直径与弹性模量对围岩稳定性影响较小。 围岩物理力学参数对围岩稳定性的影响,如图8所示。 图8 围岩物理力学参数对围岩稳定性的影响Fig.8 Influence of physical and mechanical parameters of rock mass on stability of surrounding rock 由图8可知,当围岩弹性模量由1.5 GPa增大到3 GPa时,围岩稳定系数减小了0.007;当围岩泊松比由0.25增加到0.35时,围岩稳定系数提高了0.172;这是因为当围岩弹性模量越小或者泊松比越大时,围岩变形较大,锚杆发挥的支护作用增加,使得围岩加固体的物理力学参数较岩体的物理力学参数大了许多,从而增加了围岩的稳定性,但围岩较软,变形过大也可能使锚杆屈服,失去支护效果,降低了围岩稳定性。当围岩黏聚力由0.5 MPa增大到1.5 MPa时,围岩稳定系数增加了0.589;当围岩内摩擦角由25 °增大到35°时,围岩稳定系数增加了0.530。可知,围岩黏聚力与内摩擦角对围岩稳定性影响较大,当支护参数相同时,围岩越硬,稳定性越好。 工程参数对围岩稳定性影响,如图9所示。 图9 工程参数对围岩稳定性影响Fig.9 Influence of engineering parameters on the stability of surrounding rock 由图9可以看出,围岩稳定系数随着原岩应力增加而减小,并且呈线性变化,当原岩应力由3 MPa增加到6 MPa时,围岩稳定系数减小了0.449;围岩稳定系数随着巷道半径增大而减小,当巷道半径由2.74 m增加到3.74 m时,围岩稳定系数减小了0.244。还可以看出,当原岩应力较高时,巷道开挖半径较小也能保证围岩稳定。 1)定义了围岩加固体概念,建立了围岩与加固体协调变形力学模型,提出了依靠加固体变形程度来评价围岩稳定性的方法。 2)推导出了围岩加固体物理力学参数表达式,将加固体参数带入力学模型中,导出了巷道围岩应力与位移表达式,定义了围岩稳定系数,求得了巷道洞壁位移、锚杆轴力和围岩加固体塑性区半径。 3)锚杆支护后,与岩体物理力学参数相比,加固体弹性模量和黏聚力增加了4.12%和5.7%,加固体泊松比减少了1.40%,可知,锚杆支护对围岩加固体黏聚力影响最大。 4)巷道锚杆支护设计遵循长而疏、短而密的原则,但锚杆长度增加到一定值后,锚杆长度变化对围岩洞壁位移影响很小,围岩稳定性提高的幅度在降低;锚杆预紧力与围岩稳定性成线性变化,预紧力增加到一定值后,锚杆由于屈服而失去支护效果;锚杆弹性模量与直径对为岩稳定性影响较小。 5)岩体的弹性模量与泊松比对围岩稳定性影响较小,而岩体黏聚力与内摩擦角对围岩稳定性影响较大;围岩稳定性与原岩应力呈线性变化,当原岩应力较大时,开挖半径较小也能保证围岩稳定。 [1] 辛亚军, 安定超, 李梦远. 巷道围岩再造承载层机理及数值模拟[J]. 中国安全生产科学技术, 2016, 12(6): 36-41. XIN Yajun, AN Dingchao, LI Mengyuan. Mechanism and numerical simulation of renewable bearing stratum in roadway surrounding rock[J]. Journal of Safety Science and Technology, 2016, 12(6): 36-41. [2] 孟庆彬, 韩立军, 张帆舸, 等. 深部高应力软岩巷道耦合支护效应研究及应用[J]. 岩土力学, 2017, 38(5): 1425-1433. MENG Qingbin, HAN Lijun, ZHANG Fange, et al. Coupling support effect on high-stress deep soft rock roadway and its application[J]. Rock and Soil Mechanics, 2017, 38(5): 1425-1433. [3] 王卫军, 袁超, 余伟健, 等. 深部大变形巷道围岩稳定性控制方法研究[J]. 煤炭学报, 2016, 41(12): 2922-2929. WANG Weijun, YUAN Chao, YU Weijian, et al. Stability control method of surrounding rock in deep roadway with large deformation[J]. Journal of China Coal Society, 2016, 41(12): 2922-2929. [4] 姚琦,冯涛,王卫军,等.极破碎围岩半煤岩巷变形破坏机理及支护控制研究[J]. 中国安全生产科学技术, 2015, 11(5): 32-39. YAO Qi, FENG Tao, WANG Weijun, et al. Study on deformation and failure mechanism and support control measure of half coal rock roadway under extremely fractured surrounding rock[J]. Journal of Safety Science and Technology, 2015, 11(5): 32-39. [5] 侯朝炯. 深部巷道围岩控制的有效途径[J]. 中国矿业大学学报, 2017, 46(3): 468-472. HOU Chaojiong. Effective approach for surrounding rock control in deep roadway[J].Journal of China University of Mining and Technology, 2017, 46(3): 468-472. [6] 冯月新, 尹乾, 许国安. 大断面软岩硐室稳定性控制技术[J]. 煤炭科学技术, 2016, 44(1): 90-94. FENG Yuexin, YIN Qian, XU Guoan. Stability control technology of soft rock chamber with large cross section[J]. Coal Science and Technology, 2016, 44(1): 90-94. [7] 康红普, 王金华, 林健. 煤矿巷道锚杆支护应用实例分析[J]. 岩石力学与工程学报, 2010, 29(4): 649-664. KANG Hongpu, WANG Jinhua, LIN Jian. Case studies of rock bolting in coal mine roadways[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(4): 649-664. [8] 何满潮, 张国锋, 齐干, 等. 夹河矿深部煤巷围岩稳定性控制技术研究[J].采矿与安全工程学报, 2007, 24(1): 28-31. HE Manchao, ZHANG Guofeng, QI Gan, et al. Stability Control of Surrounding Rocks in Deep Entry of Jiahe Coal Mine[J]. Journal of Mining& Safety Engineering, 2007, 24(1): 28-31. [9] 肖同强, 李怀珍, 支光辉. 深部厚顶煤巷道围岩稳定性相似模型试验研究[J]. 煤炭学报, 2014, 39(6): 1016-1022. XIAO Tongqiang, LI Huaizhen, ZHI Guanghui. Experimental study on similar simulation for surrounding rock stability of deep roadway with thick top coal[J]. Journal of China Coal Society, 2014, 39(6): 1016-1022. [10] 徐立功, 李浩, 陈祥林, 等. 锚杆参数对围岩稳定性影响的数值分析[J]. 岩土工程学报, 2010, 32(S2): 250-252. XU Ligong, LI Hao, CHEN Xianglin, et al. Numerical analysis on the impact of rock bolt parameters on stability of surrounding rock[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(S2): 250-252. [11] 李宁, 刘乃飞, 李国峰. 软岩及土质隧洞围岩稳定性评价新方法[J]. 岩石力学与工程学报, 2014, 33(9): 1812-1814. LI Ning, LIU Naifei, LI Guofeng. New method for stability evaluation of soil and soft rock tunnels[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(9): 1812-1814. [12] 侯朝炯, 勾攀峰. 巷道锚杆支护围岩强度强化机理研究[J]. 岩石力学与工程学报, 2000, 19(3): 342-345. HOU Zhaojiong, GOU Panfeng. Mechanism study on strength enhancement the surrounding roadway supported by bolt[J]. Chinese Journal of Rock Mechanics and Engineering, 2000, 19(3): 342-345. [13] 戴怡文, 王卫华, 孙道元, 等. 深部采场进路开采顶板稳定性分析与支护设计[J]. 中国安全生产科学技术, 2018, 14(2): 33-38. DAI Yiwen, WANG Weihua, SUN Daoyuan, et al. Roof stability analysis and support design in drift mining of deep stope[J]. Journal of Safety Science and Technology, 2018, 14(2): 33-38. [14] PAN Q J, DIAS D. Safety factor assessment of a tunnel face reinforced by horizontal dowels[J]. Engineering Structures, 2017, 142: 56-66. [15] ANAGNOSTOU G, PERAZZELLI P. Analysis method and design charts for bolt reinforcement of the tunnel face in cohesive-frictional soils[J].Tunnelling and Underground Space Technology, 2015, 47: 162-181. [16] PELIZZA S, KIM S H, KIM J S. A study of strength parameters in the reinforced ground by rock bolts[C]. Seoul:Proceedings of the World Tunnel Congress and 32nd ITA Assembly, 2006,21(3):378-379. [17] 杨双锁, 张百胜. 锚杆对岩土体作用的力学本质[J]. 岩土力学, 2003, 24(10): 280-282. YANG Shuangsuo, ZHANG Baisheng. The influence of bolt action force to the mechanical property of rocks[J]. Rock and Soil Mechanics, 2003, 24(10): 280-282. [18] 侯朝炯. 深部巷道围岩控制的关键技术研究[J]. 中国矿业大学学报, 2017, 46(5): 972-976. HOU Chaojiong. Key technologies for surrounding rock control in deep roadway[J]. Journal of University of Mining & Technology, 2017, 46(5): 972-976.4 算例分析
4.1 求解算例



4.2 锚杆支护参数对围岩稳定性影响分析
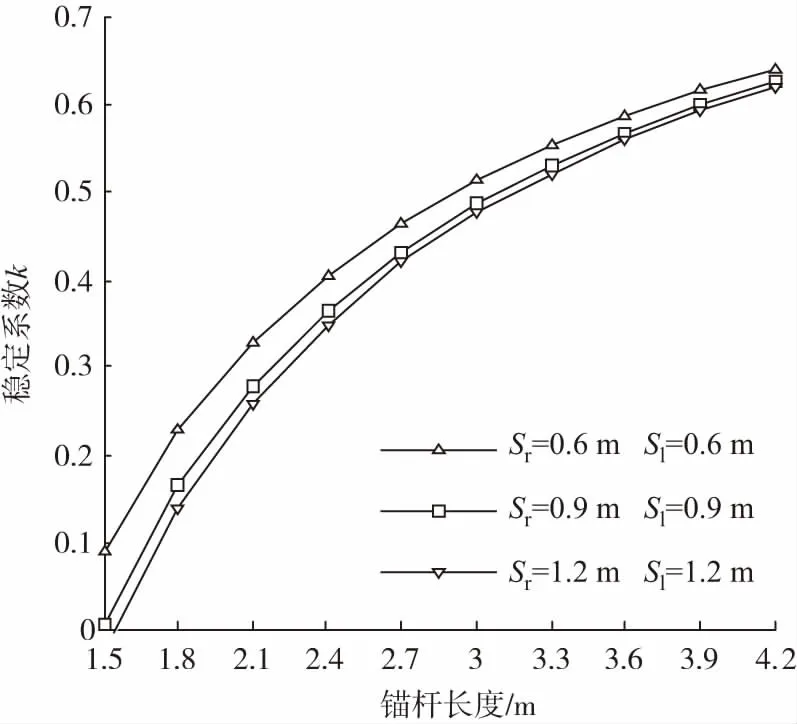
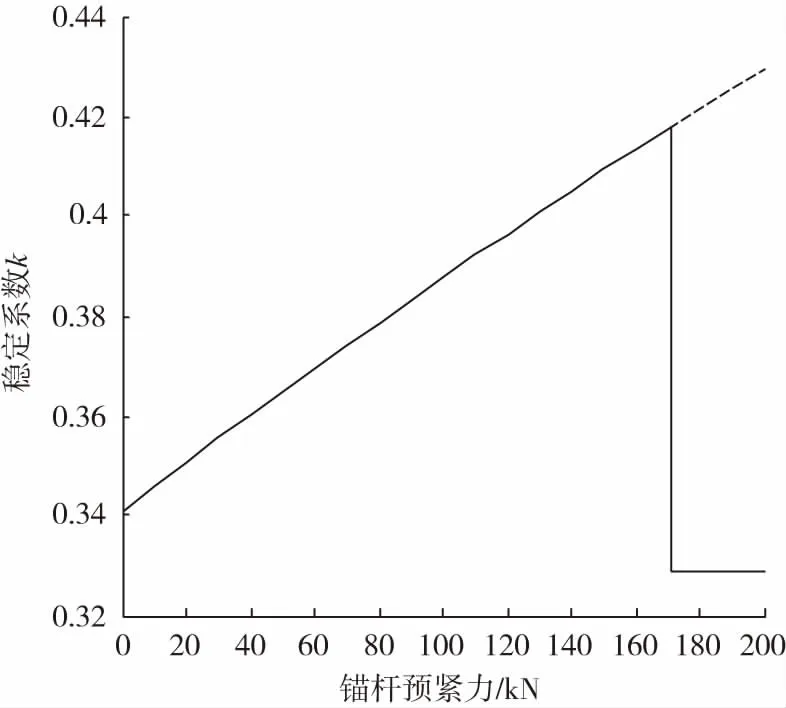
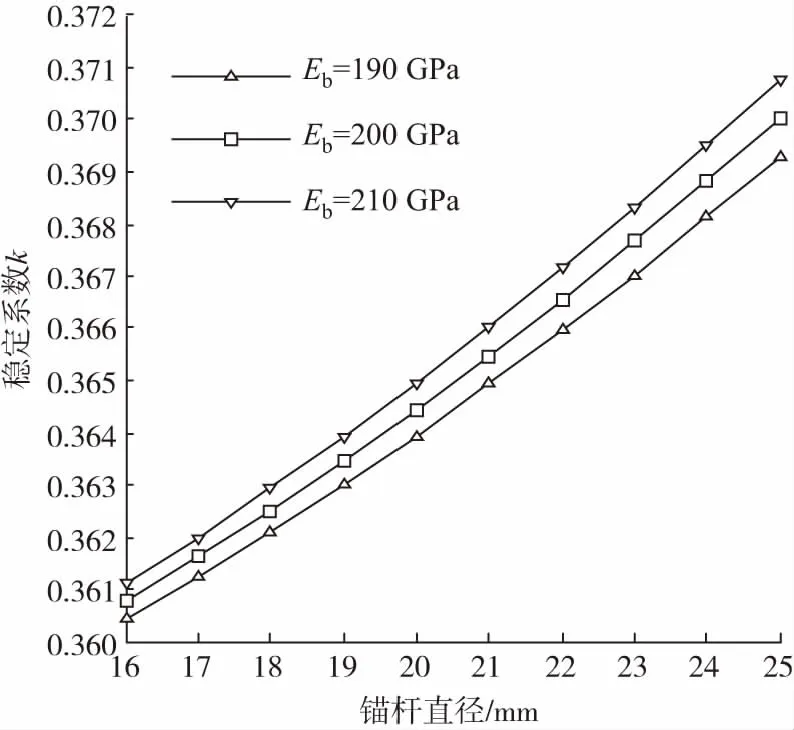
4.3 围岩物理力学参数对围岩稳定性的影响分析

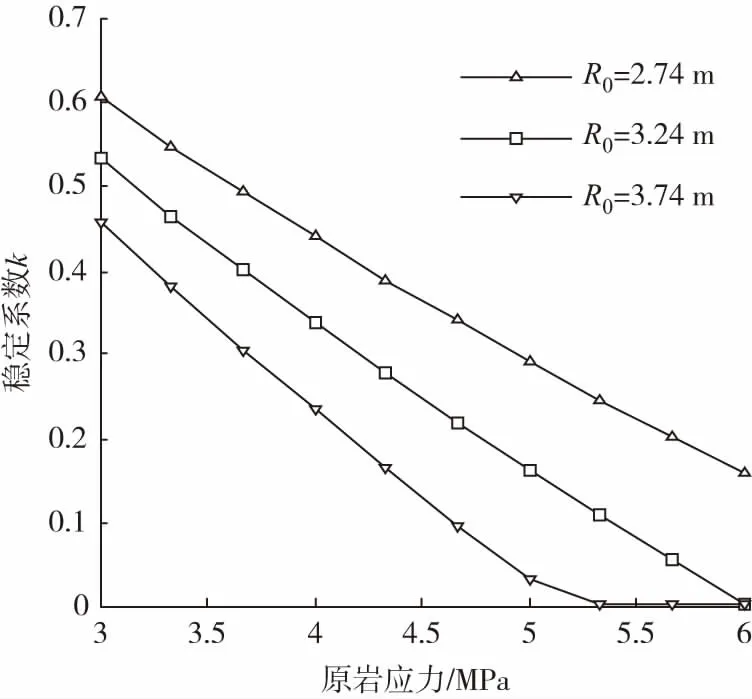
4.4 工程参数对围岩稳定性影响分析
5 结论
