基于角度二分法的NC代码转换理论和试验研究

2018-06-04刘纪凯赵庆志张兴武梁奉兴张林华

山东理工大学学报（自然科学版） 2018年4期

刘纪凯，赵庆志，张兴武，梁奉兴，张林华

(1.山东理工大学机械工程学院，山东淄博 255049；2.辰欣药业股份有限公司，山东济宁 272100；3.山东新华医疗器械股份有限公司，山东淄博 255000)

Abstract: In order to make the general NC machine process the workpieces which are represented by difference interpolation NC code, a method for the high-precision approximation curve using multi-segment micro line is studied based on angle dichotomy.This method overcame the shortcomings of the great calculation difficulty of equal error method and the overdense curve nodes of equal space method. Through the test of OpenGL viewport graphic simulation and machining experiments, this method achieved the conversion from the differential interpolation of NC code into ordinary NC code, and the program is running stable and reliable with friendly interface easy to use, and obtained the ideal processing effect.

Keywords:the method of angle dichotomy; the differential interpolation; the transformation of the NC code; approximation error; OpenGL

现行数控机床插补器广泛采用逐点比较法、数字积分法(DDA)、最小偏差法、数据采样法等[1-6]，加工图元以直线和圆弧为主.而特殊插补理论，如差分插补理论[7]，不仅有直线、圆弧，还有圆锥曲线族(椭圆、抛物线、双曲线)加工图元和其他加工图元等.因此，普通数控机床无法完全识别特殊插补理论的数控加工代码，也就无法完成工件的加工.在现有数控装备条件下，只有通过代码之间的转换才能加工特殊代码表示的工件，而通过手工编程又无法实现高精度的加工，鉴于此情况，以差分插补数控加工代码为例研究了特殊数控加工代码向普通数控加工代码的转换.

1 代码转换总体流程规划

由于现行数控机床识别直线(G00/G01)、圆弧(G02/G03)代码，所以要将差分插补数控加工代码转换为直线、圆弧代码.对差分插补代码中的直线、圆弧代码不需做处理，椭圆、抛物线、双曲线代码的处理流程如图1所示.

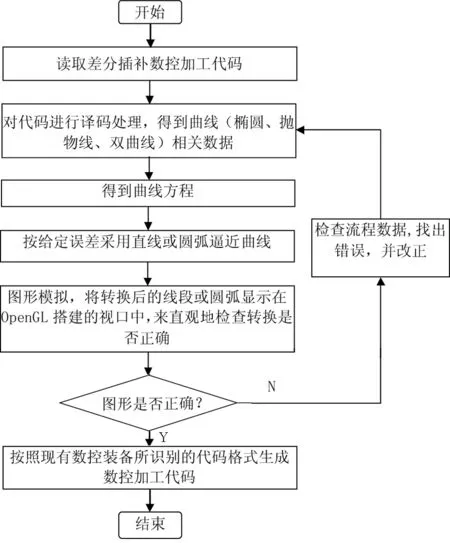
图1 代码转换流程图Fig.1 Code conversion flow chart

2 基于角度二分法的NC代码转换理论研究

在满足给定精度要求前提下，为减少计算量、提高代码转换速度，采用多段微线段(直线)逼近曲线.直线逼近曲线的主要方法有等误差法和等间距法.由于涉及二次曲线，所以采用等误差法存在较大的计算难度，会影响计算速度与精度[8]；采用等间距法会导致曲线上节点过于密集，从而使所产生的直线数控加工代码量增大[9].

由于圆锥曲线方程可以转换为以角度为参变量的参数方程，为克服等误差法与等间距法存在的缺点，提出了一种基于角度二分理论的多段微线段逼近曲线的误差模型.

2.1 直线逼近曲线误差模型

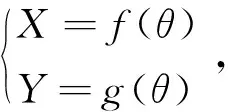
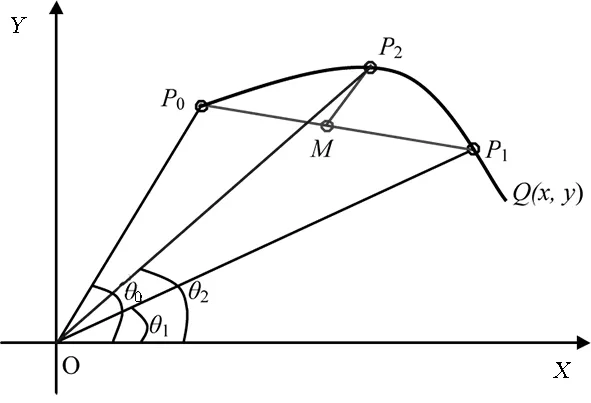
图2 逼近误差模型Fig.2 Approximation error model

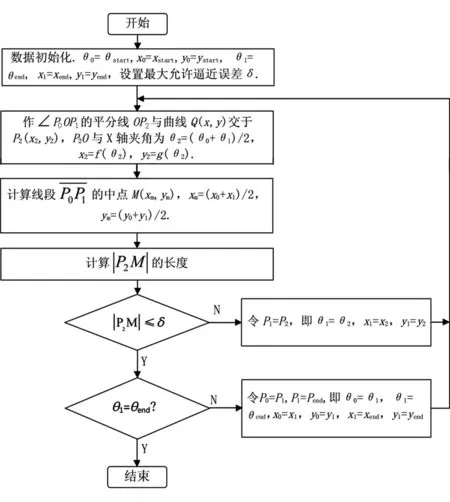
图3 基于角度二分法的微线段逼近曲线流程图Fig.3 Flow chart of micro line approaching curve based on angle dichotomy

2.2 误差模型在圆锥曲线中的应用

根据上述误差模型实现多段微线段逼近圆锥曲线，以达到差分插补NC代码向普通NC代码(直线或圆弧)转换之目的.设定所允许最大逼近误差δ为0.001mm，由于现行机床识别圆弧代码，这里只讨论椭圆、抛物线和双曲线代码.

2.2.1 误差模型在椭圆中的应用

以代码G91 G05 X-10 Y-10 I-5 J-5 A10 B5.7735为例进行说明.A表示椭圆在X方向上的轴长度，B表示在Y方向上的轴长度，(I,J)为椭圆中心相对弧起点的位置，(X,Y)为弧终点相对起点的位置[7].由于椭圆参数方程为

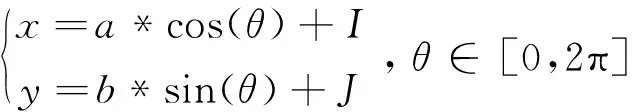
(1)

所以可由代码数据得到椭圆方程

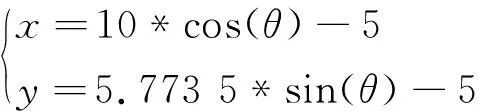
(2)

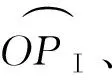
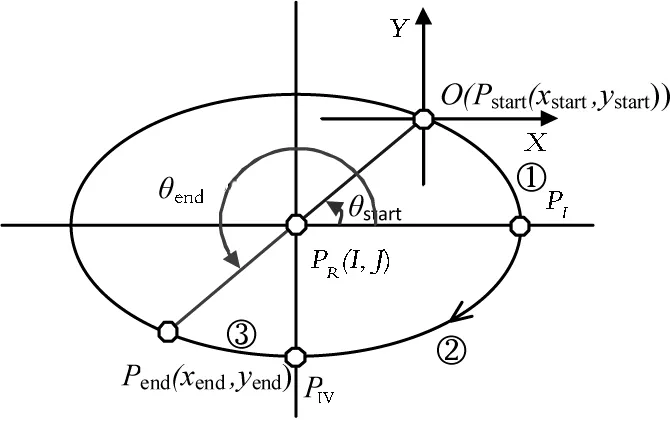
图4 误差模型在椭圆中的应用Fig. 4 Application of error model in ellipse

2.2.2 误差模型在抛物线中的应用

以代码G91 G07 X15 Y15 I-5 J5 K0为例进行说明.由文献[7]可知，K=0表示抛物线对称轴平行于X轴，(I,J)为抛物线顶点相对弧起点的位置，(X,Y)为弧终点相对起点的位置.由于对称轴平行于X轴的抛物线参数方程为

(3)

所以可由代码数据得到抛物线方程

(4)

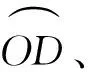
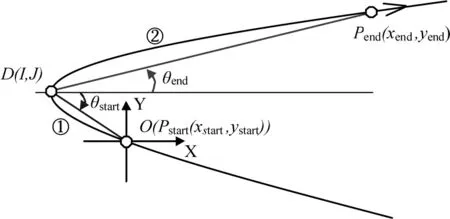
图5 误差模型在抛物线中的应用Fig. 5 Application of error model in parabola

2.2.3 误差模型在双曲线中的应用

以代码G91 G9 X15 Y17.64911 I-5 J5 A10 K0为例进行说明.由文献[7]可知，K=0表示双曲线实对称轴平行于X轴，A为实半轴的长度，(I,J)为双曲线顶点相对弧起点的位置，(X,Y)为弧终点相对起点的位置.由于实对称轴平行于X轴的双曲线参数方程为

如图6所示，以实半轴长度a为半径，以双曲线对称中心O为圆点作圆C0，双曲线上的点Pend向实对称轴作垂线，过垂足Pe″作圆C0的切线(切点Pe′在双曲线对称中心O与双曲线上的点Pend之间)，θ为Pe′O与实对称轴之间的夹角(逆时针方向).

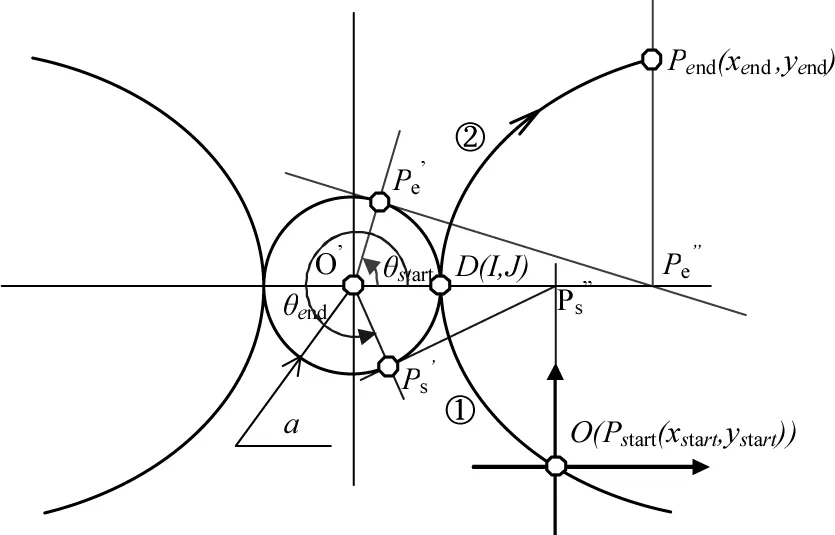
图6 误差模型在双曲线中的应用Fig. 6 Application of error model in hyperbola

由代码数据得到双曲线方程

(5)

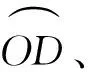
3 图形仿真

为直观观察代码转换是否正确，减少不必要的工件浪费、时间浪费，节约成本，在VC++6.0下搭建三维OpenGL视口，实现图形平移、缩放、3D漫游浏览[10].由于OpenGL只提供直线显示的库函数，所以对OpenGL下的圆弧显示做如下研究.

由于OpenGL函数库中无圆弧函数，所以需要自定义函数来实现圆弧的图形显示.为适应数控加工代码，定义两个函数分别为顺圆弧(ShunArc(double m_X0, double m_Y0, double m_X1, double m_Y1, double m_Z,double m_I, double m_J))和逆圆弧(NiArc(double m_X0, double m_Y0, double m_X1, double m_Y1, double m_Z,double m_I, double m_J)),入口参数为圆弧起点、圆弧终点、当前Z坐标值和圆心相对起点的坐标值.

for(θ=θstart; θ>=θend; )

{glBegin(GL_LINES);

glVertex3f(Xc+ r*cos(θ),Yc+ r*sin(θ),m_Z);

θ=θ-Δθ;

glVertex3f(Xc+ r*cos(θ),Yc+ r*sin(θ),m_Z);

glEnd();}

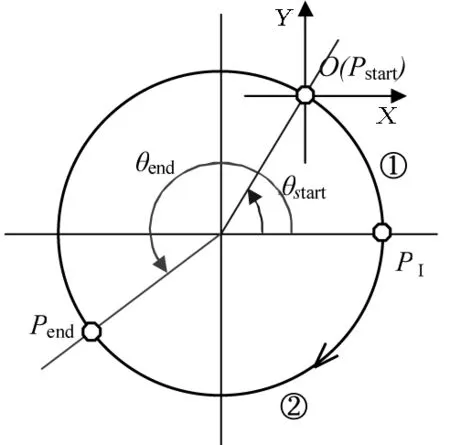
图7 OpenGL中顺圆弧图形显示Fig.7 The clockwise circular graphics in the OpenGL viewport display

4 加工实例

4.1 获取目标数控加工代码

差分插补NC代码向普通NC代码转换的具体操作流程如图8所示.

图8 差分插补源代码Fig.8 Source codes of differential interpolation

1)打开代码转换设置界面(图9)，点击载入“差分插补代码”按钮，打开代码文件装入代码或按照界面上差分插补代码格式写入数控加工代码，拟合模式选择直线，允许最大误差为0.001mm，代码格式选择绝对坐标，点击“设置完成”退出设置界面.

2)点击图10中的“数据准备”按钮，进行代码转换的相关数据计算.

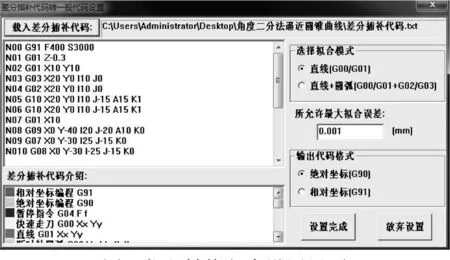
图9 代码转换程序设置界面Fig.9 Codes conversion program settings interface

图10 图形模拟Fig.10 Graphic simulation

3) 当提示数据准备完成时，点击“图形模拟”按钮，生成模拟图，并进行检查，若错误则分析程序生成的中间过渡数据，找出错误并改正.

4) 若3)中图形无误，则点击“刀路模拟”按钮，生成刀路图11，检查刀路是否正确，若不正确检查刀路数据文件.

5) 若4)中刀路无误，点击“获取代码”按钮，获取目标数控加工代码，当提示获取完成时，点击“保存代码”按钮，选择存储路径并保存代码.

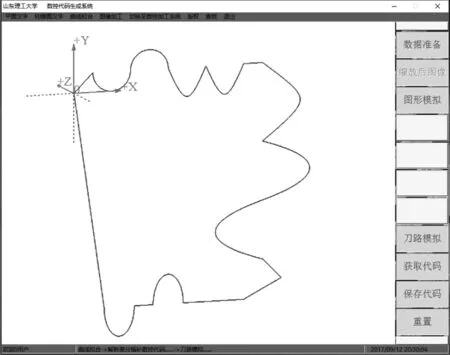
图11 刀路模拟Fig.11 Tool path simulation

图12 目标数控加工代码截图Fig.12 Target NC machining code screenshot

4.2 对目标数控加工代码进行加工

获取了图12所示的1792行代码后，将获取的数控加工代码载入数控机床中在PVC板材上进行加工，加工现场、加工进行中、加工完成图如图13～图16所示.

图13 加工现场图Fig.13 Machining site picture

图14 数控机床对目标数控代码执行中Fig.14 NC machine tool for target NC code execution

图15 加工完成图Fig.15 Processing complete picture

图16 局部放大图Fig.16 Partial enlarged picture

4.3 对差分插补代码进行直接加工

在能够识别差分插补代码的机床上对图8所示差分插补代码进行了直接加工，图17为代码仿真图，图18为加工完成图，图19为局部放大图.

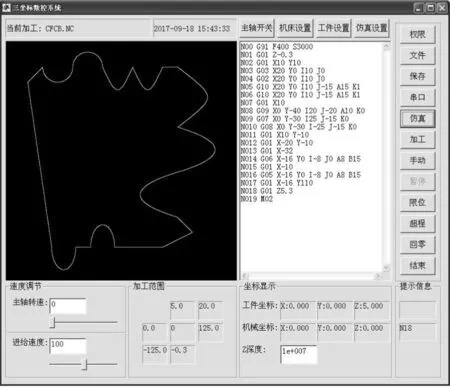
图17 差分代码仿真图Fig.17 Difference code emulation picture

图18 加工完成图Fig.18 Processing complete picture

图19 局部放大图Fig.19 Partial enlarged picture

由4.2试验(试验结果为图15和图16)和4.3差分插补代码加工实验(实验结果为图18和图19)对比可知，转换后的代码正确无误，通过加工得到了预期的图形，且放大后曲线轮廓光滑无折线感.证明了基于角度二分法的多段微线段逼近曲线方法正确无误、精度高.对连续多段代码的正确处理显示了该算法的鲁棒性非常好，达到了预期的效果.