盈亏平衡分析方法在建设工程项目中的应用

李曦

【摘要】在工程项目的投资效益评价中，对预测指标的不确定性分析是一项非常重要的工作，而盈亏平衡分析作为经济效果评价中不确定性分析的一种重要方法在建筑工程项目中的应用非常重要。本文将对盈亏平衡分析方法的模型进行探讨，对盈亏平衡分析于工程项目中的一些实际应用进行讨论。

【关键词】盈亏平衡分析；量本利；成本；應用

一、盈亏平衡分析概述

盈亏平衡分析又称“本一量一利”分析或“量本利”分析，成本一业务量一利润间的关系是成本管理中一组最基本的、最重要的核心关系，而“量一本一利”分析法是解析这一组关系的最有力工具。根据销售收入及成本与产销量之间是否成线性关系，盈亏平衡分析又可分为线性和非线性盈亏平衡分析，通常都是指线性盈亏平衡分析。

盈亏平衡分析以变动成本为基础，对企业的产销量、销售收入、成本、利润进行综合分析，将技术方案投产后的产销量作为不确定因素，通过计算技术方案的盈亏平衡点的产销量，判断经济效果的影响程度。

盈亏平衡分析具有简单有效、实用性强、使用范围广等特点，从多角度及各种假定条件下对企业的计划、决策等提供丰富的财务诊断分析资料，具有良好的诊断切入角度。小到一个技术方案、大到一个企业的经营生产，运用盈亏平衡分析变动成本法，可以掌握盈亏界限，分析经营状况，其用途不仅限于计算盈亏平衡点，在相当范围的未来假设情况下，可以用来考查收入、费用和预测可实现的利润。

二、盈亏平衡分析方法

（一）总成本与固定成本、可变成本

根据成本费用与产量的关系可将技术方案总成本费用分解为可变成本、固定成本和半可变成本。

固定成本是指在技术方案一定的产量范围内不受产品产量影响的成本，如工资及福利费、折旧费、修理费、无形资产等。

可变成本是随技术方案产品产量的增减而成正比例变化的各项成本，如原材料、燃料、动力费、包装费和计件工资等。

半可变成本指介于固定和可变成本之间，随技术方案产量增长而增长，但不成正比例变化，如与生产批量有关的消耗性材料费用、模具费及运输费等，这部分成本随产量变动一般是呈梯形曲线。由于半可变成本通常在总成本中占比很小，在技术方案经济效果分析中，可根据行业特点将产品半可变成本分解成固定成本和可变成本。长期借款利息应视为固定成本：流动资金借款和短期借款利息部分与产品产量相关，其利息可视为半可变成本，为简化计算，一般也将其作为固定成本。

综上，技术方案总成本是固定成本和可变成本之和，与产品产量的关系也可近似地认为是线性关系，即：

C=CF+CU×Q

式中C——总成本（下同）；CF——固定成本（下同）；CU——单位产品变动成本（下同）；Q——产量（或工程量）（下同）

（二）销售收入与营业税金及附加

1.销售收入

技术方案的销售收入与产品销量的关系有两种情况。

（1）该技术方案的生产销售活动不会明显地影响市场供求状况，假定其他市场条件不变，产品价格不会随该技术方案的销量的变化而变化，可以看作是一个常数，销售收入与销量呈线性关系。

（2）该技术方案的生产销售活动将明显地影响市场供求状况，随着该技术方案产品销量的增加，产品价格有所下降，这时销售收入与销量之间不再是线性关系。

在通常的效果评价分析中，为便于计算，均按销售收入与销量呈线性关系这种情况考虑。

2.营业税金及附加

由于单位产品的营业税及附加是随产品的销售单价变化而变化的，为便于分析，将销售收入与营业税金及附加合并考虑。

经简化后，技术方案的销售收入是销量的线性函数，即：

S=p×Q-TU×Q （2）

式中S——销售收入（下同）；p——单位产品售价（下同）；TU——单位产品营业税金及附加（当投入产出都按不含税价格时，TU不包括增值税）（下同）

为便于模型计算，有时在给定模型数据时，往往把产品售价p设定为已扣除税金及附加的价格，即：

S=p×Q （3）

（三）量本利模型

在一定期间把成本总额分解简化为固定成本和变动成本后，再把收入和利润加进来，成本、产量和利润的关系就可以统一于一个数学模型，然后根据数学模型绘制平衡图。

为便于分析计算，简化数字模型，对盈亏平衡分析通常做如下假设：

生产量等于销售量；产销量变化时，单位可变成本不变，总生产成本是产销量的线性函数；产销量变化，销售单价不变，销售收入是产销量的线性函数；只生产单一产品，或生产多种产品但可按单一产品计算，不同产品的生产负荷率的变化保持一致。

盈亏平衡分析的表示方式可以分为方程式法和图示法。

1.方程式法

盈亏平衡分析的关系方程式主要有两种：损益方程式和边际贡献方程式。

（1）损益方程式

损益方程式是利润表的高度概括和模型化。即首先确定一定时间的收入，然后计算这些收入相对应的成本，两者之差为期间利润：

B=S-C

（4）

式中B——利润（下同）。将式（1）、式（3）代入式（4）可得：

B=p×Q-CU×Q-CF （5）

式（5）明确表达了量本利之间的数量关系，是基本的损益方程式。它含有相互联系的5个变量，给定其中4个，便可求出另一个变量的值。

在通常的技术方案、企业规划中，一般把产品单价、单位变动成本、固定成本视为稳定常量，只有销量和利润2个自由变量。给定销量时，可计算出预期利润；给定目标利润时，可计算出应达到的产销量。

上述基本的损益方程式是最基本的.实际上是损益表的模型化表达，不同的损益表可构建不同模型。比如包含期间成本的损益方程式：根据“多步式损益表”，不但要分解产品成本，而且要分解销售、管理、财力等期间费用。根据对产品成本的分解思想，同样可以对期间费用进行分解，构建模型方程式变为：

税前利润=销售收入-（变动销货成本+固定销货成本）-（变动期间费用+固定期间费用）=（单价-单位变动成本-单位变动期间费用）×销量-（变动期间费用+固定期间费用）

再比如计算税后利润的损益方程式：所得税是根据企业应税所得和所得税税率计算的，并从利润总额中扣除，既非变动成本也非固定成本，构建模型方程式变为：税后利润=税前利润总额×（1-所得税税率）=（单价×销量-单位变动成本×销量-固定成本）×（1一所得税税率）

以上增加了变量的模型虽然更为复杂.但更接近现实真实情况，能更好地进行盈亏平衡分析。 （2）边际贡献方程式 边际贡献是销售收入减去变动成本以后的差额，即：

Cm=S-Cu×Q （6）

式中Cm——产品边际贡献（下同）

如果用单位产品表示，则方程式为：

C'm=P-Cu （7）

式中C'm——单位产品边际贡献（下同）

边际贡献，是产品扣除自身变动成本后给企业所做的贡献，它首先用于回收企业的固定成本，如果还有剩余则成为利润，如果不足以收回固定成本就发生亏损。由于变动成既包括生产制造过程的变动成本，也包括期间变动成本，所以，边际贡献也分为制造边际贡献和产品边际贡獻（本文采用产品边际贡献）。

制造边际贡献=销售收入-产品变动成本

产品边际贡献=制造边际贡献-期间变动成本=销售收入-产品变动成本-期间变动成本

边际贡献率，是指边际贡献在销售收入中所占的比率，同理，指边际贡献也分为制造边际贡献率和产品边际贡献率（本文采用产品边际贡献率）。边际贡献率可以理解为每1元的销售收入由边际贡献所占的比重，它反映产品给企业做出贡献的能力。与边际贡献率相对应的概念是“变动成本率”，即变动成本在销售收入中所占的比率。

Rcm=Cm/S

Rcm=[（P-CU）×Q]/（P×Q）

Rcm=（P-Cu）/P （8）

式中Rcm——产品边际贡献率（下同）；Cm——产品边际贡献（下同）

那么在基本的损益方程式中代入“边际贡献”，即分别将式（7）、式（8）代入式（4）可得

B=p×Q-Cu×Q-CF

B=（p-CU）×Q-CF

B=Cm×Q-CF （9）

B=Rcm×P×Q-CF （10）

即描述为：利润=产品边际贡献×销量-固定成本

=产品边际贡献率×单价×销量-固定成本

=产品边际贡献率×销售收入-固定成本

即：B=Rcm×S-CF （11）

这个方程式既可以用于单一产品也可以用于多种产品的企业，在计算多种产品时，只需计算出多种产品的加权平均边际贡献率，并以此代替方程式中的单一产品的边际贡献率。

2.图示法

图示法因其能清晰地显示出评价对象既不盈利又不亏损时达到的产销量，又称为盈亏临界图或损益平衡图。用图形表达量本利的相互关系，不仅形象直观而且容易理解。

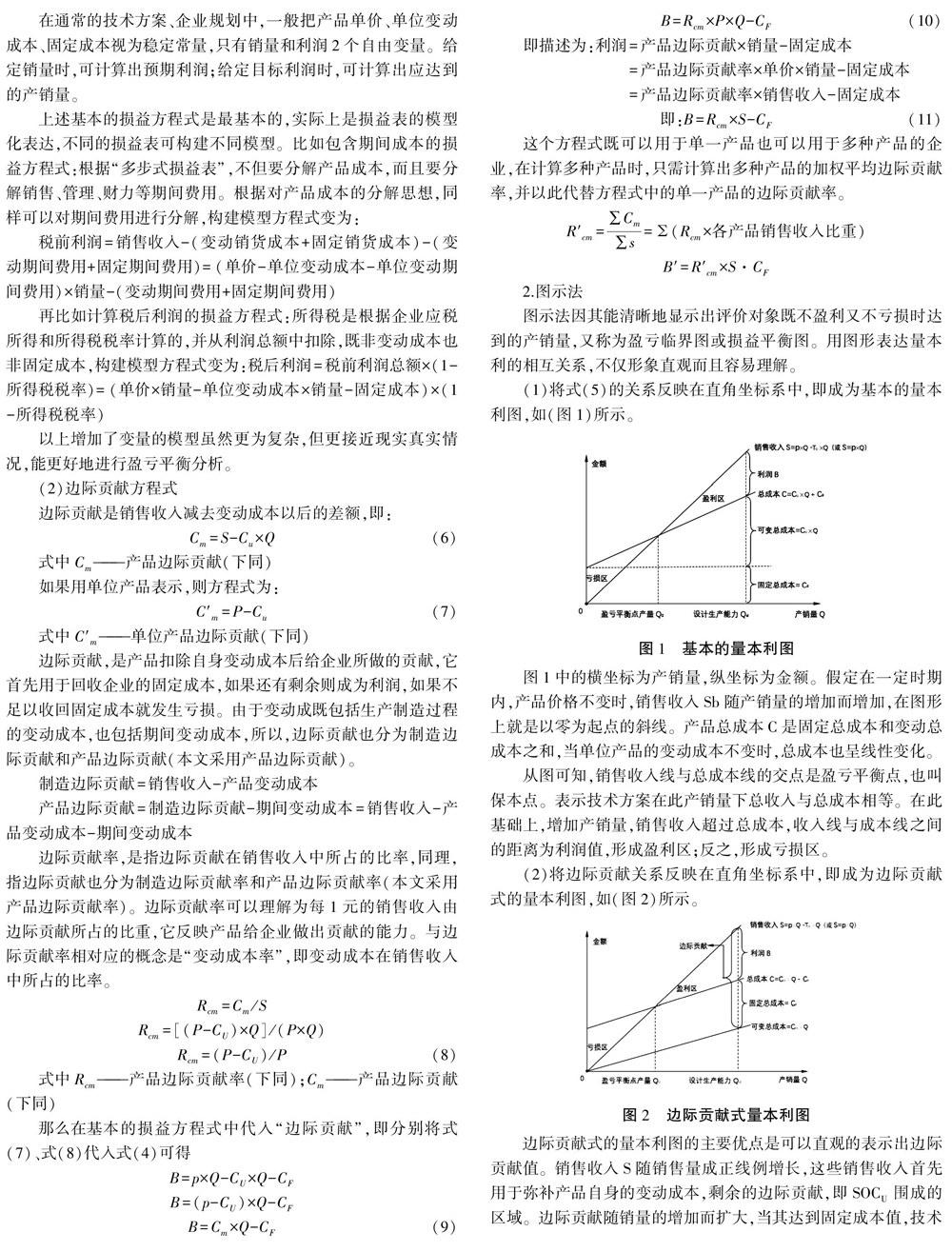
（1）将式（5）的关系反映在直角坐标系中，即成为基本的量本利图，如（图1）所示。

图1中的横坐标为产销量，纵坐标为金额。假定在一定时期内，产品价格不变时，销售收入sb随产销量的增加而增加，在图形上就是以零为起点的斜线。产品总成本c是固定总成本和变动总成本之和，当单位产品的变动成本不变时，总成本也呈线性变化。

从图可知，销售收入线与总成本线的交点是盈亏平衡点，也叫保本点。表示技术方案在此产销量下总收入与总成本相等。在此基础上，增加产销量，销售收入超过总成本，收入线与成本线之间的距离为利润值，形成盈利区；反之，形成亏损区。

（2）将边际贡献关系反映在直角坐标系中，即成为边际贡献式的量本利图，如（图2）所示。

边际贡献式的量本利图的主要优点是可以直观的表示出边际贡献值。销售收入s随销售量成正线例增长，这些销售收入首先用于弥补产品自身的变动成本，剩余的边际贡献，即SOC。围成的区域。边际贡献随销量的增加而扩大，当其达到固定成本值，技术方案处于盈亏临界状态，当边际贡献超过固定成本后，技术方案进行盈利状态。

三、盈亏平衡分析应用

从图1可见，当企业在小于Q0的产销量下组织生产，则技术方案亏损；反之技术方案盈利。显然产销量Q0盈亏平衡点（BEP）的一个重要表达。就单一产品技术方案来说，盈利临界点的计算并不困难，一般是从销售收入等于总成本即盈利平衡方程式中导出：

式中r——营业税金及附加的税率

对技术方案运用盈亏平衡点分析时应该注意：盈亏平衡点要按技术方案投产达到设计生产能力后正常年份的产销量、变动成本、固定成本、产品价格、营业税金及附加等数据来计算，而不能按计算期内的平均值计算。正常年份一般选择还款期间的第一个达产年和还款后的年份分别计算，以便分别给出最高和最低的盈亏平衡点区间范围。

【例1-1】某施工企业准备投资建设一个商品混凝土拌合站，技术方案年设计生产能力75万方混凝土，年固定成本为550万元，各标号混凝土销售价格平均为390元/方，单方混凝土可变成本320元/方，混凝土税金及附加税率为3.36%。该企业的市场销售人员需保证拿回多少方混凝土订单才不致亏本？在订单充足且达到设计生产能力时盈利多少？

解：根据产销量盈亏平衡可知

计算结果表明，要让拌合站不亏损，销售人员必须保证能拿回96667.6方混凝土订单。当订单量大于96667.6时，拌合站盈利。

B=p×Q-CU×Q-CF-TU×Q

=390×75-320×75-550-390×3.36%×75

=3717.2万元

计算结果表明，在订单充足且达到设计生产能力时盈利3717.2万元。

【例1-2】某施工企业新购一台盾构机价值4300万元，设计寿命总掘进lO公里，每年正常施工隧道2.8公里，残值100万元，修理费等其他固定费用每年252万元，盾构机施工单位可变成本为6500元/米。现有3份业主合同可供企业选择签订，合同l中盾构隧道掘进单价、工程量分别为13000元/米、2500米，合同2中盾构隧道掘进单价、工程量分别为12000元/米、3600米，合同3中盾构隧道掘进单价、工程量分别为11500元/米、3900米，税金及附加税的税率均为12.32%。现该企业须选择签订一份合同，那么签订哪份合同书经济上对自己最为有利呢？签订合同后企业会盈利（或亏损）多少？按掘进单价12000元/米来计算的话，该盾构机设计寿命期内能盈利多少？

解：分析以上数据，3份合同书的合同金额可计算出来，分别为2080万元、4320万元4485万元，合同3金额最高，那么它是不是最理想的呢？

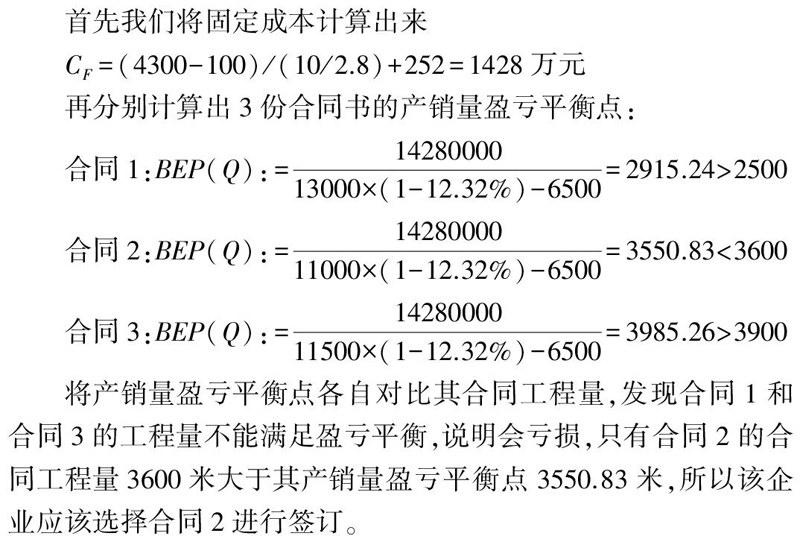
首先我们将固定成本计算出来

CF=（4300-100）/（10/2.8）+252=1428万元

再分别计算出3份合同书的产销量盈亏平衡点：

将产销量盈亏平衡点各自对比其合同工程量，发现合同l和合同3的工程量不能满足盈亏平衡，说明会亏损，只有合同2的合同工程量3600米大于其产销量盈亏平衡点3550.83米，所以该企业应该选择合同2进行签订。 选择合同2，B=1.2×3600-0.65×3600-1428-1.2×12.32%×3600=19.776万元

盾构机设计寿命期内：B=1.2×10000-0.65×10000-1428-1.2×12.32%×10000=2593.6万元

计算结果表明，签订合同2最为理想，其盈利金额为19.776万元，盾构机设计寿命期内能盈利2593.6万元。

四、盈亏平衡分析的限制与不足

盈亏平衡分析作为一种不确定性经济评价方法，虽然能够从市场适应性方面说明技术方案风险的大小，但不能揭示产生技术方案风险的根源。

盈亏平衡分析多侧重于线性方面的研究，对于非线性分析因难以确定收入、成本函数的情况而存在着较大的困难。对于线性分析也做了一些假设条件和模型简化.其计算结果的说服力当然也随之打了折扣。进行盈亏平衡分析前必须要做收入和成本函数两方面的具体分析，然而，到目前为止，还没有一套完善、可靠的方法來确定非线性盈亏平衡分析中的收入、成本函数。

参考文献：

[1]刘建涛.盈亏平衡分析技术——原理与应用[M].电子工业出版社，1989

[2]韩良智.动态盈亏平衡分析与应用[M].工业技术经济，2003

[3]于俊年.计量经济学[M].对外经济贸易大学出版社，2000