一种伺服驱动定位末端抖振问题的抑制分析及解决办法

韦 凤

（广州市机电技师学院，广东广州 510435）

1 问题提出

在永磁交流伺服传动系统中，在定位时存在振动问题（比如在机器手臂运动停止时容易发生晃动），称之为位置末端抖振，通常这种振动在机械结构确定后，表现为振动频率点固有。在抑制该固有频率振动时，又要尽量减小对其他运动频率成分的影响。因此，工程上会选用陷波滤波器进行抖振抑制。本文就采用一种对位置末端抖动抑制的滤波器进行选型分析，在实验中与低通滤波器进行对比。

2 滤波器的选型

工程上容易实现且效果明显的陷波滤波器，通常选用二阶的。最为典型的是双T型陷波滤波器，传递函数如公式（1）所示。

在实际应用中，为了达到更好的调试效果，需要对公式（1）进行改进，在双T型陷波滤波器中增加滤波器的陷波深度的可调参数c，这样可以同时调整陷波滤波器的工作频率、陷波宽度和陷波深度，如公式（2）所示：

在改进型滤波器传递函数中，定义三个重要的参数：

陷波作用频率ω0：产生陷波作用的固有频率值；

陷波带宽系数k1：在陷波作用下，影响系统幅值增益低于-3 dB的频率带宽；

陷波深度系数k2：影响滤波器的陷波深度。

为形象改进型双T型陷波滤波器幅频特性曲线，可见图1。滤波器的陷波作用在频率ω0点处最为明显，使得幅值增益降至最低。再将滤波器的陷波带宽记为Bw，陷波深度记为Dp。陷波带宽Bw、陷波深度Dp与系数k1、k2的关系如公式（3）所示：

参考滤波器设置相关文献可知，增大系数k1以加宽陷波带宽，或者降低系数k2以加深陷波深度，均会导致陷波作用频率ω0附近的相角滞后。因此，在设计滤波器时，只能考虑陷波带宽、陷波深度和相频特性之间的相对平衡。在保证滤波带宽、深度能够抑制末端低频抖振的情况下，尽可能减小滤波带宽、深度取值，从而减少相角滞后。

图1 改进型双T网络陷波滤波器幅频特性

3 陷波滤波器离散化

上述滤波器选型给出了连续系统中的陷波滤波器传递函数，并且分析了滤波器的参数影响。而要将其进行数字化应用，需通过离散化的方法将连续系统中的滤波器转化为离散系统中的数字滤波器。考虑到后向差分法等效离散化的结构简单、容易实现，构成系统稳定性强，最终选用该法对公式（2）进行等效离散化处理。

将s=代入式（2），可得：

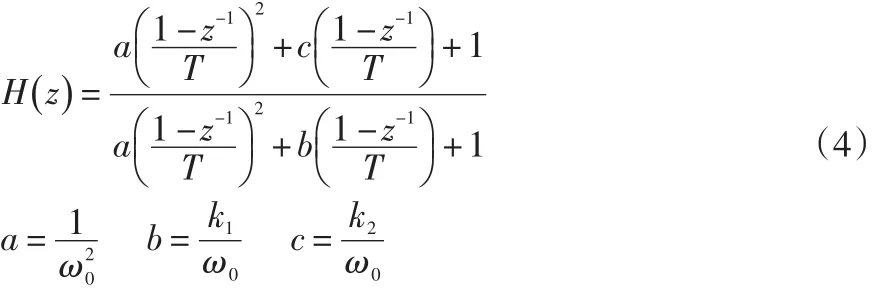
化简，得到陷波滤波器的离散传递函数H(z)：

将公式（5）所示离散传递函数，换算成关于X（z），Y（z）的差分方程，进而可得到数字滤波器，如公式（6）所示。

4 定位末端抖振抑制分析

伺服系统中位置环控制采用比例+前馈控制方法，若控制参数选用不合适，当运行条件发生变化时（例如负载转动惯量发生变化、运行指令有高速启停要求等），加上位置环调节存在滞后因素，会导致系统控制性能变差，伺服系统在定位时会发生超调甚至抖振现象。对伺服系统而言，要抑制定位时末端的抖动，应将减震滤波器加在位置指令之后，滤除位置指令中的抖振频率成分，进而达到消减振动的目的。定位末端抖动抑制框架如图2所示。

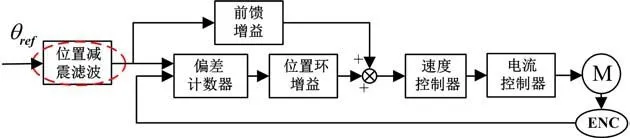
图2 定位末端抖动被动滤波抑制框图

位置减震滤波分为低通滤波和陷波滤波，其传递函数分别为公式（7）和式（8）。

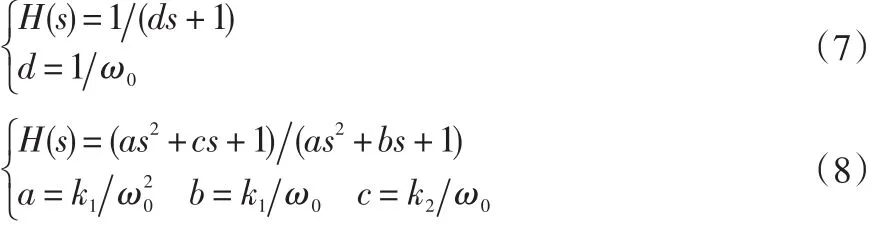
低通滤波器用新极点引入的过阻尼效果校正系统的极点引起的欠阻尼震荡，综合之后得到较好的系统性能。低通滤波将滤波频率前的幅频特性拉低，消除了抖振点，但对之前的频段均有影响，且相对于未加滤波的情况相频特性存在较大的滞后。

陷波滤波器通过引入两个共轭零点和共轭极点来改善系统的幅频特性。陷波滤波器的共轭零点的取值要求与滤波前系统中引起抖振的共轭极点尽可能一致，从而达到零极点相消的目的。同时由陷波滤波器的共轭极点则成为了新系统的主导极点，经根轨迹分析，其阻尼比接近1，可认为滤波后系统接近无阻尼状态。由此可见陷波滤波器仅对滤波频率点出的幅频特性产生抑制作用，这一点性能优于低通滤波器。

5 实验验证末端抖振

本实验目的为验证定位末端抖振抑制在不同工况下的适用性，并将采用陷波滤波器和改进低通滤波器两种处理方式对比，寻找最适合实际应用的方案。

采用不同惯量盘进行定位末端抖振抑制测试，采用的仪器是GS驱动器与电机，LabVIEW采集卡，实验平台如图3所示。

图3 测试平台

通过实验，观察转速为450 r/min左右的抖振抑制情况，测试改变惯量对系统的影响，小惯量采用2个惯量盘，大惯量采用4个惯量盘，通过改变Kp值，得到转速和位置随时间的变化曲线，测试条件及结果如表1所示。

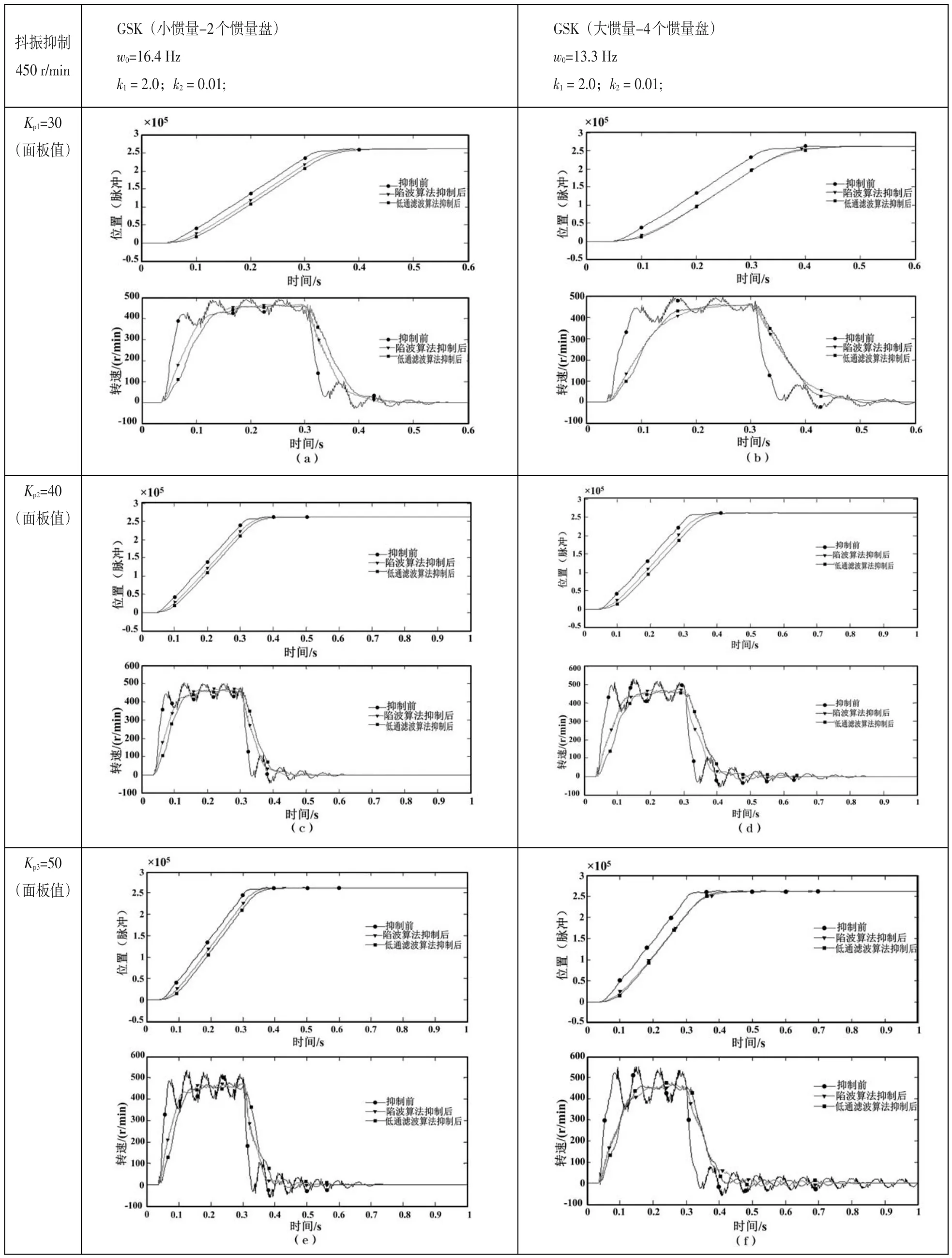
表1 末端抖振抑制测试条件及结果

6 结论

（1）由上表可知，为了测试改变惯量对系统的影响，分别测试了2个惯量盘和4个惯量盘下的各组实验。通过测试可知，惯量的改变影响系统的抖振频率，陷波滤波器所用算法能较好地抑制定位末端抖振情况。

（2）保证了负载定位时稳定性。但由于滤波器滞后的相角特性，会为系统引入滞后的相角误差，降低了伺服系统的快速跟随性能。对比说明，陷波滤波器的位置响应滞后情况优于低通滤波器，但是仍然有较大的相角误差，需要进一步的消除。

7 位置相角滞后的补偿方法

为了补偿相角滞后的问题，采用一种对位置指令系统重构的方法，其结构图如图4所示，引入补偿系数。

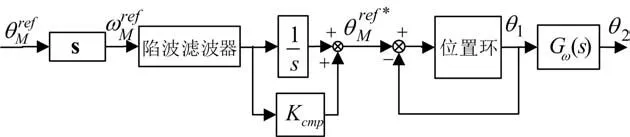
图4 加滤波的位置环系统模型框图

采用GS驱动器与电机（130SJT-100DA41）完成本次补偿对比试验。实际振动频率ω0约为7 Hz，此时可以得到此时补偿系数为Kcmp实际调试为0.02。图5为补偿方案的抑制效果，其中图（a）为位置响应，图（b）为速度响应。可以看出加入补偿环节后，不仅抑制了伺服系统定位末端抖动，而且相位滞后比单纯用陷波滤波器引起的相位滞后小。

实验中两种陷波滤波方案的响应滞后时间对比，其中陷波滤波器的响应滞后为275 ms，基于陷波滤波器的补偿方案的响应滞后时间为175 ms。实际测试与理论分析和仿真结果吻合。

8 总结

在基于辨识得到的伺服系统定位末端抖振频率，尝试采用各种被动滤波方式进行定位末端抖动抑制。并详尽地实验测试了采用低通滤波器和陷波滤波器的抑制效果，通过对比发现陷波滤波器效果更好，并在陷波滤波的基础上提出了相角补偿方案。

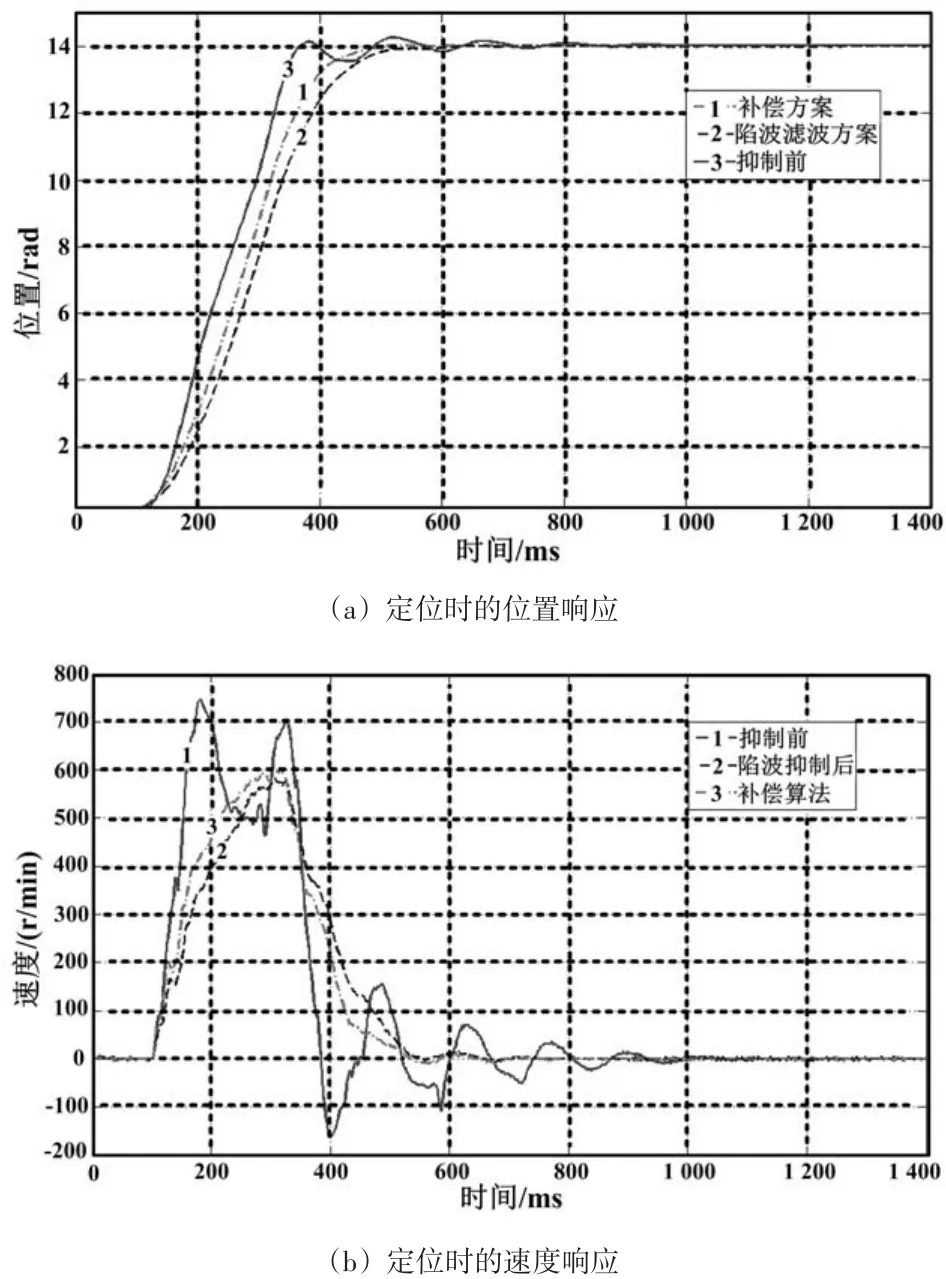
图5 补偿方案的抑制效果

实验表明：通过位置环参数整定后，基于陷波滤波器的相位补偿方案能较好地抑制弹性负载条件下伺服系统定位末端抖动，同时引入的相位滞后比单纯用陷波滤波器时要小。该方案适用于对机器手臂、自动化流水线传输的末端抖动抑制。

［1］杨辉，范永坤，舒怀亮.抑制机械谐振的一种改进的数字滤波器 ［J］.光电工程，2004，31（S1）：30-39.