基于Nastran的汽车仪表管梁模态分析与优化

张 劼，谢 健※，高 明，张 骏

（1.江苏信息职业技术学院汽车工程学院，江苏无锡 214153；2.无锡市智碗科技有限公司，江苏无锡 214000）

0 引言

计算模态分析是利用有限元计算方法来获取研究对象固有振动特性的一种研究方法。通常计算可得研究对象包含的多个模态，每个模态都具有特定的固有频率、阻尼比和模态振型。

通过进一步计算，还可得到各类设计参数变化对结构性能的影响大小，即参数的灵敏度。利用灵敏度方法就能有效优化研究对象的各设计参数，从而提高振动性能。

在汽车设计制造过程中，良好的振动性能是关键要素之一，直接影响到汽车的运行稳定性、结构安全性及使用舒适性。利用有限元软件进行模态仿真分析，可以有效掌握相关零部件或整车的振动性能，进而预测其与传动系、路面激励等相互作用的可能性；通过基于灵敏度方法的设计参数优化达到避开共振频率、提升振动性能的目的。同时，这种方法减少了样车制造次数与试验次数，并为试验提供了一定依据，大幅节省开发费用、缩短开发周期，已成为汽车设计制造过程中必不可少的环节。本文以某型汽车仪表管梁为研究对象，利用Nastran软件进行计算模态分析与优化。

1 计算模态分析与灵敏度分析的理论基础

将研究对象划分成有限个单元，此时对象就拥有了有限个自由度。对此有限自由度系统，其运动方程为：

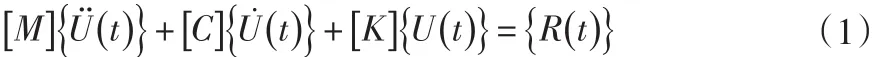
式（1）中，[M]为质量矩阵，[C]为阻尼矩阵，[K]为刚度矩阵，{Ü(t)}、{U˙(t)}、{U(t)}分别为系统的加速度向量、速度向量和位移向量，{R(t)}为激振力向量。

模态属于系统固有特性，与外部激励条件无关，求解自由振动方程即可，此时{R(t)}=0。同时，阻尼对系统的模态影响也不大，因此也可略去阻尼项，得到系统的无阻尼振动方程为：

假定系统为简谐运动，则其位移向量可表示为：

其中，{Φ}为位移向量的幅值，ω为简谐运动的角频率。将式（3）代入式（2）中，可得：

欲使{Φ}有非零解，则

解此方程可得一组离散根ωi（i=1，2，…，n），对应得到一组{Φi}（i=1，2，…，n）。ωi与{Φi}即为系统第i阶固有频率与振型。

振动性能优化需要研究的是固有频率下设计参数的灵敏度，因此对式（4）在固有频率ωi和振型{Φi}下求设计参数αi的偏导数，得：

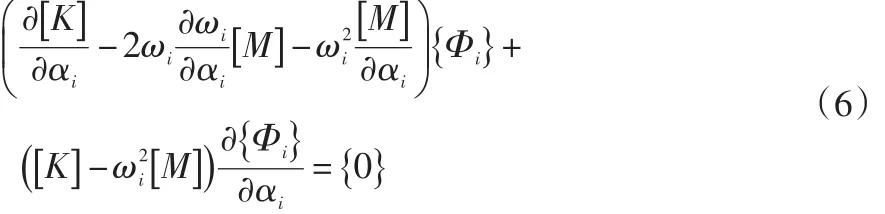
式（6）整理化简后可得固有频率ωi下参数αi的灵敏度为：

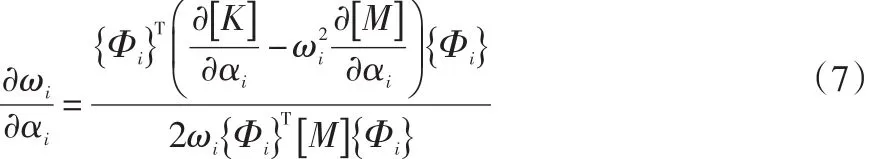
2 有限元模型建立

2.1 几何模型与材料参数

如图1所示为该车仪表管梁结构的几何模型。管梁结构主要由横梁、辅助梁及一系列支架焊接而成，通过螺栓将管梁两端的横梁支架与车身固定在一起，从而实现管梁总成的安装。为满足结构刚度、强度设计需求，管梁各构件必须使用适合的材料并具备一定厚度。本文管梁为全钢结构，总重7.752 kg，钢材密度为7 850 kg/m3，弹性模量为210 GPa，泊松比为0.3，各焊接件厚度如表1所示。

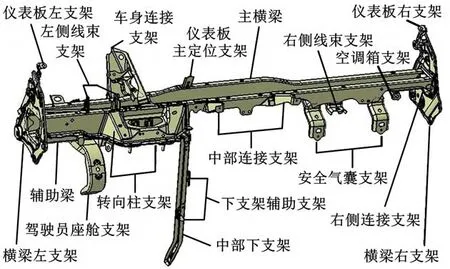
图1 仪表管梁几何模型

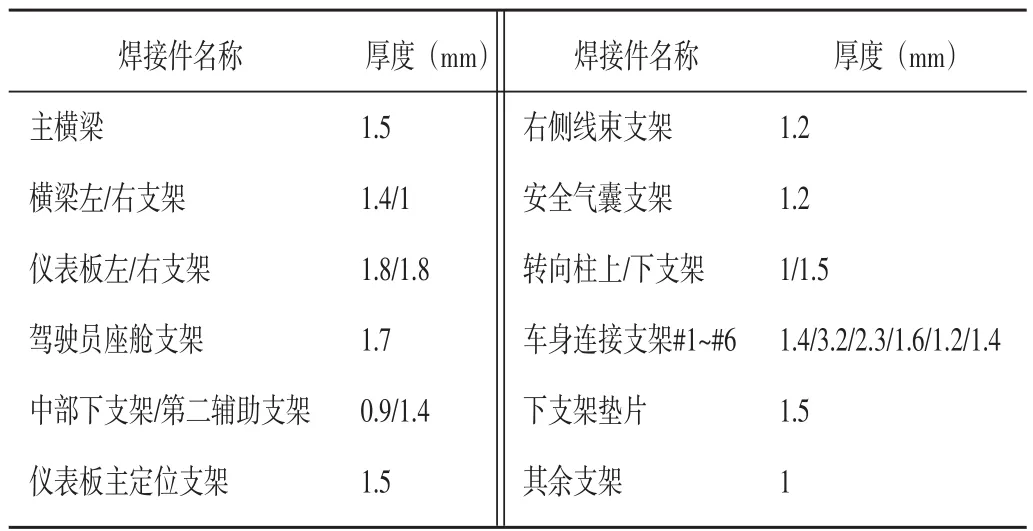
表1 仪表管梁焊接件厚度

2.2 网格划分与前处理

由于管梁焊接件厚度尺寸远小于其他方向尺寸，故采用壳单元（SHELL）简化几何实体模型较为合理。将几何模型抽中面后定义为壳单元，并且赋予表1的厚度值。

针对管梁壳单元模型的网格划分以四边形为主、三角形为辅，网格尺寸与质量控制采取全局统一标准，如表2所示。生成单元总数18 167个，其中四边形单元16 968个、三角形单元1 199个，划分效果如图2所示。

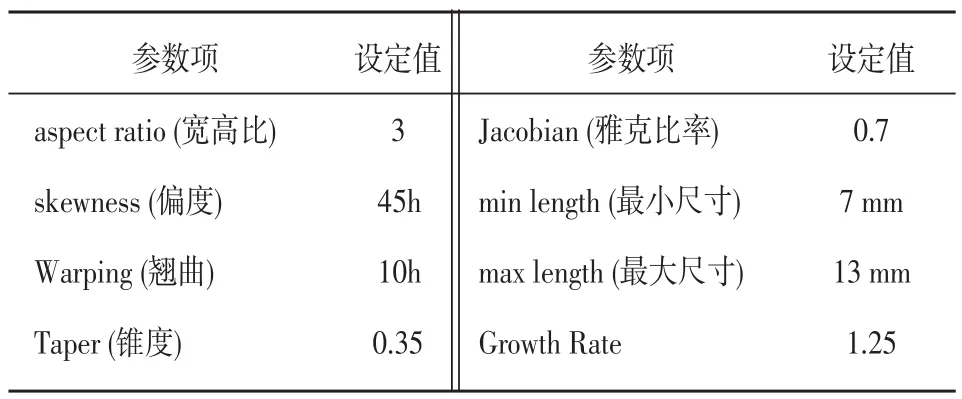
表2 网格划分参数设置标准

图2 网格划分效果

管梁各焊接件间的焊点使用RBE3-HEXA-RBE3方式模拟：将焊点表达为一个六面体实体，并弹性连接到焊件表面，焊点直径统一为5 mm[1-2]，如图3所示。螺栓连接处使用RBE2方式模拟：将螺栓孔周围的网格节点刚性连接到孔的中央，表明螺栓对孔周围的固定作用，如图4所示。

由于管梁的左右横梁支架、中部下支架以及车身连接支架都与车身利用螺栓固定，故对模型相应位置施加固定约束。这种约束模态与工程实际边界条件相吻合，具备较高的精确度和可对比性。

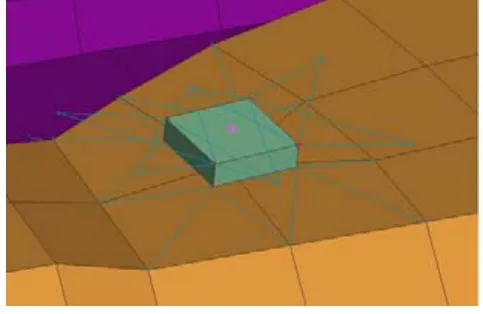
图3 焊点模拟

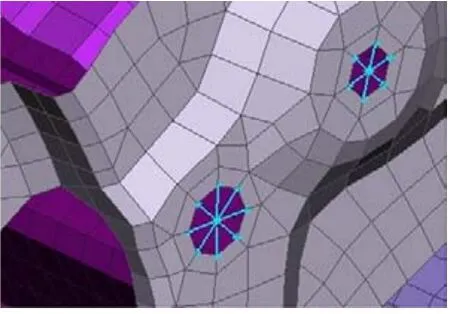
图4 螺栓模拟

3 仿真结果分析及优化

3.1 管梁模态仿真结果分析

针对管梁的前10阶模态展开有限元计算，表3所示为每阶模态的振动频率及振态。可以看到，第3阶为全局弯曲模态，第8阶为全局扭转模态，其余为局部模态，这主要是将支架从整车提取出来后装配约束减少造成的。图5和图6为两个全局模态的位移云图。全局模态是管梁振动性能的关键，其频率必须避开汽车怠速及正常行驶时的发动机振动频率。该车型发动机的怠速频率为27 Hz，正常行驶频率为53～137 Hz，因此其全局弯曲模态频率与怠速频率非常接近，容易产生共振现象影响振动性能。

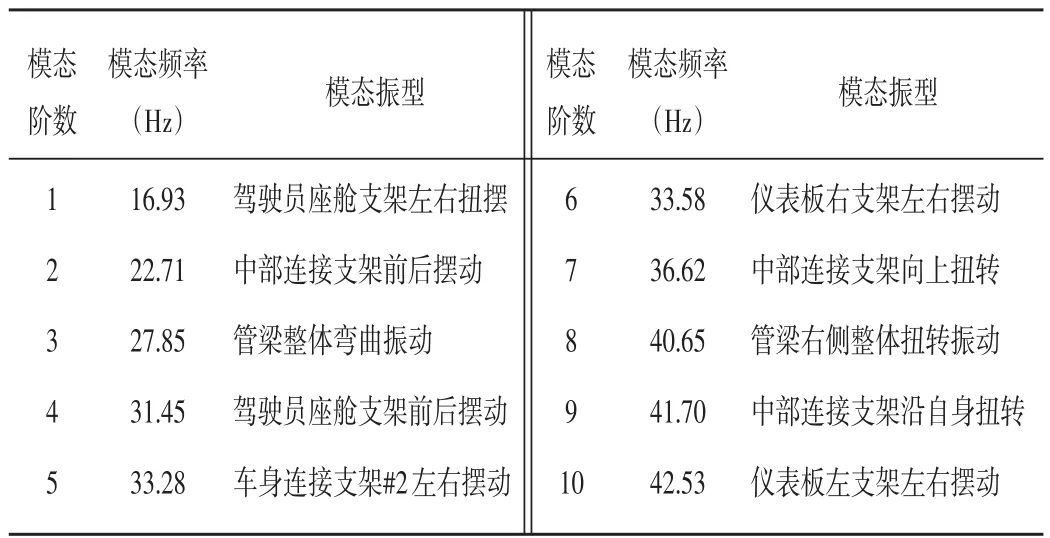
表3 管梁模态仿真结果

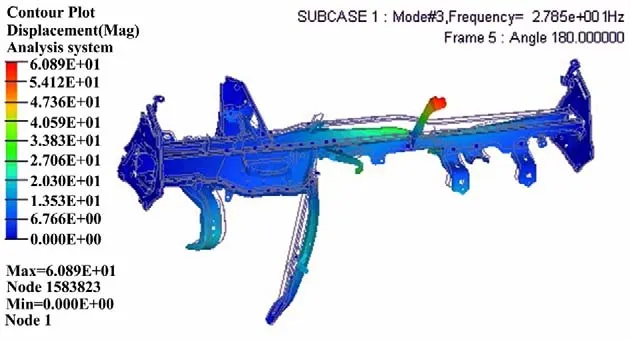
图5 管梁全局弯曲模态位移云图

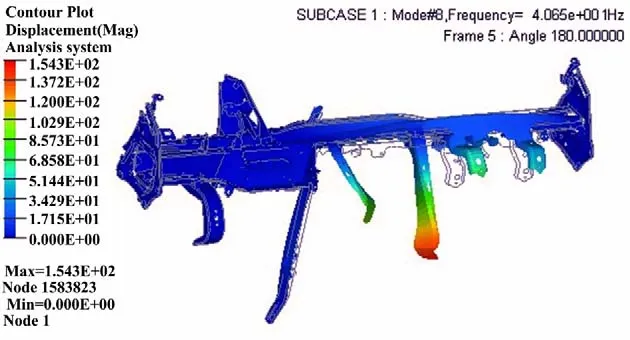
图6 管梁全局扭转模态位移云图

3.2 管梁各焊接件灵敏度分析

在模态优化前，需要判定对模态影响较大的关键部件。因此，将管梁各主要焊接件厚度设置为设计参数，将管梁第3阶频率、第8阶频率和质量设置为结构响应，利用Nastran软件SOL200求解器得出灵敏度分析结果[3][4][5]，如表4所示。

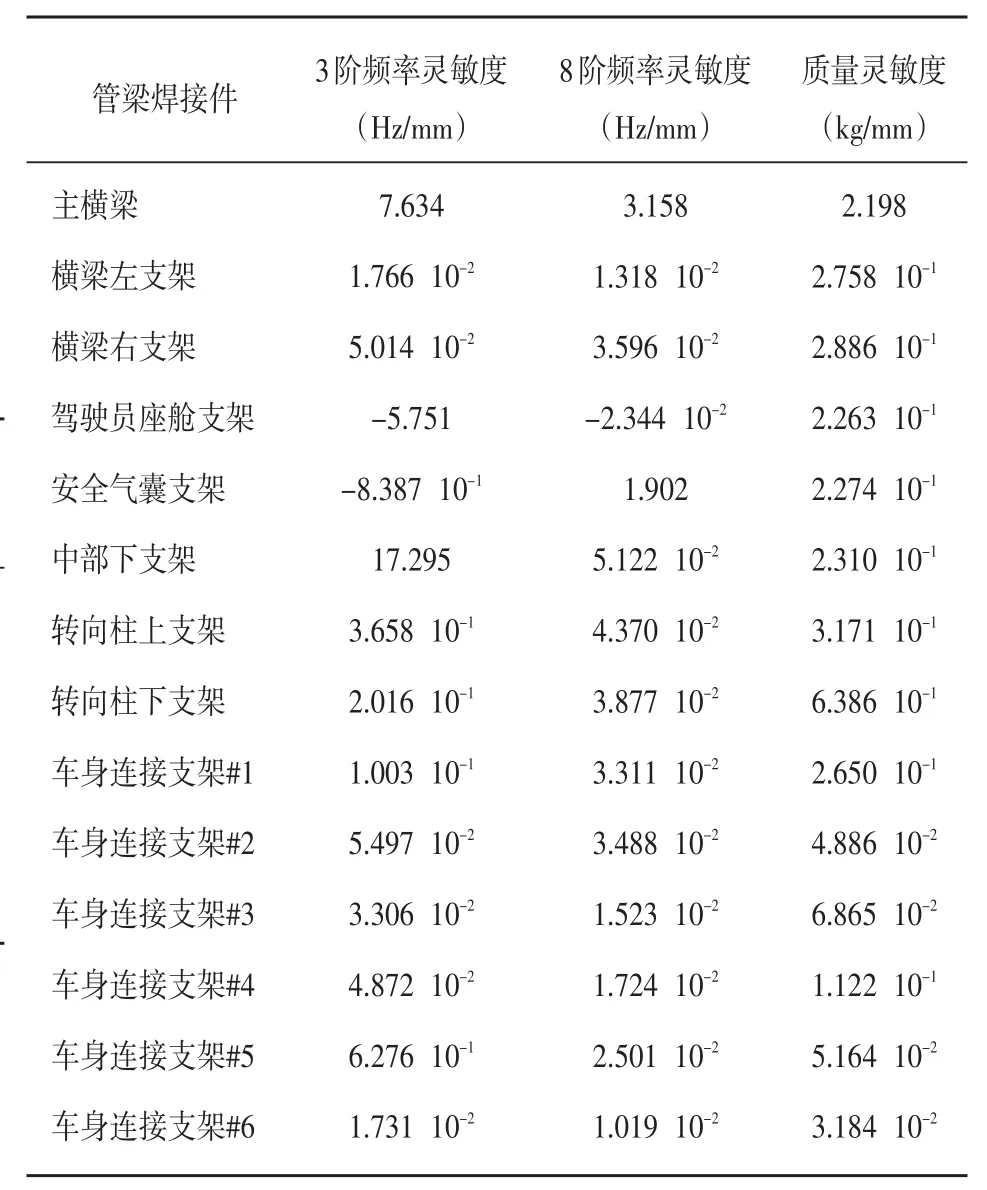
表4 管梁焊接件灵敏度分析结果

由表中数据可知：3阶频率下灵敏度较大的焊接件是主横梁、驾驶员座舱支架和中部下支架；8阶频率下灵敏度较大的焊接件是主横梁和安全气囊支架。由于优化目的是使3阶模态的振动频率避开怠速频率，因此主横梁、驾驶员座舱支架和中部下支架是模态优化的关键部件。

3.3 管梁优化分析

根据上述分析，本次模态优化以主横梁、驾驶员座舱支架以及中部下支架的厚度作为设计变量，并根据制造工艺将其最小变化量设为0.05 mm；以管梁总质量增重不超过5%以及管梁3阶频率作为约束方程；以管梁3阶频率最大化作为优化目标。通过Nastran的优化计算，得到关键部件设计参数的优化值，其与原始值的对比、优化中设置的上下限以及对质量的影响如表5所示。

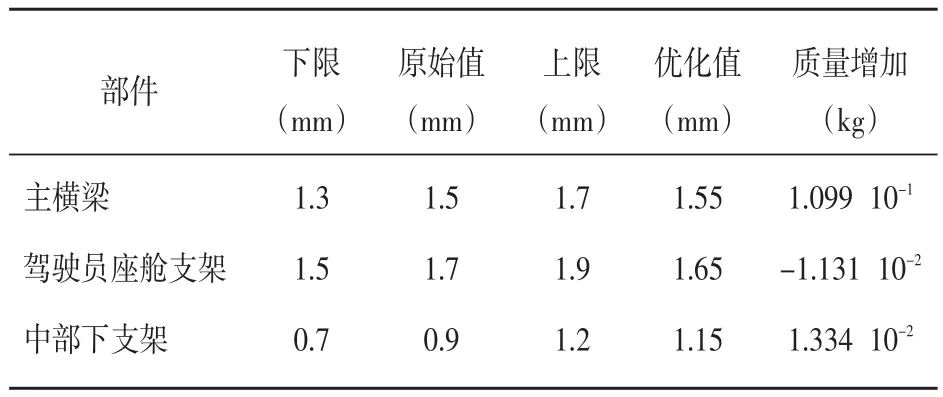
表5 关键部件优化结果

经过优化后，管梁整体质量增加1.119 10-1kg，与原设计相比增重1.44%，在允许范围内。对优化后的模型再次进行模态仿真计算，得到3阶频率为33.59 Hz，8阶频率为41.07 Hz，避开了发动机怠速及正常行驶时的振动频率，性能得到优化。

4 试验分析

4.1 管梁模态试验方案

针对仪表管梁的结构特点，采取以下方法进行试验：

（1）试验中管梁的约束方法与仿真分析保持一致；

（2）采用单点激励、多点响应的测试方法，激励方式为锤击瞬态激励；

（3）采用20次激励信号平均，减小随机噪声干扰的影响；

（4）锤击点选为主横梁中部上方，避开了1～10阶仿真模态的节点，减少模态遗漏可能；

（5）采用6个三向传感器拾振，全件设置300个测点，分50组测量，减少模态遗漏可能；

（6）关心频率为0～50 Hz[6]。

4.2 试验结果分析

图7 管梁模态频响函数

如图7所示为试验得到的管梁模态频响函数曲线。由试验结果可知，三阶全局模态为31.75 Hz，避开了怠速频率，改善了振动性能。仿真结果相对试验值误差为5.8%，模拟较为精确。

5 总结

本文通过计算模态分析的方法，研究了某型汽车的仪表管梁模态。利用灵敏度分析与设计参数优化计算，提高管梁的振动性能。最后通过试验进行验证，主要结论如下：

1）原管梁三阶与八阶模态为全局模态，其中三阶模态与汽车怠速频率非常接近，易产生共振，优化后管梁三阶模态频率得到提高，避免了怠速共振；

2）计算模态分析与优化的结果和模态试验较为吻合，可利用其缩短开发设计周期和费用；

3）有限元模型必须具备一定规模，尽可能减少简化并具备详细的约束条件和各类参数，以提高仿真分析与优化的精度[7]；

4）模态试验时对管梁的约束、激励必须合理，拾振取点必须具备规模，尽可能减少简化从而提高试验的精度。

［1］宋海生，史文库，龙岩，等.整车模态分析中焊点模拟方法的研究［J］.汽车工程，2011，33（11）：920-923.

［2］高书娜，邓兆祥，胡玉梅.车身点焊连接有限元模拟方法研究［J］.汽车工程，2008，30（9）：811-815.

［3］邬广铭，史文库，刘伟，等.基于模态灵敏度分析的客车车身优化［J］.振动与冲击，2013，32（3）：41-45.

［4］朱茂桃，陈亚洲.基于灵敏度方法的车门模态优化［J］.重庆交通大学学报（自然科学版），2014，33（1）：139-143.

［5］田德旺，田冠男，杨晋，等.汽车转向系统避免怠速共振的模态优化方法［C］.2007年MSC.Software中国用户论文集，2007.

［6］李磊，应怀樵，董书伟，等.汽车白车身模态试验与结果分析［C］.第十九届和第二十届全国振动与噪声高技术及应用会议论文集，2007.

［7］周定陆.汽车有限元模态分析与试验模态分析比较［C］.2002年MSC.Software中国用户论文集，2002.