基于多阶分数离散切比雪夫变换和产生序列的图像加密方法

肖斌，史文明，李伟生，马建峰

（1. 重庆邮电大学计算智能重点实验室，重庆 400065；2. 西安电子科技大学计算机学院，陕西 西安 710071）

1 引言

随着网络和多媒体技术的快速发展，信息的获取和传输变得日益快捷方便。图像因其直观生动、信息丰富，得以在互联网中广泛传播。然而很多图像由于涉及多种隐私和利益，并不想被非法用户获取到，因此，如何安全地在网络中传输图像成为一个非常重要的课题。图像加密技术可以在图像传播前进行加密以隐藏原始信息，是一种有效解决图像安全问题的方法。

目前，图像的加密可以在空间域和变换域进行，空间域主要利用图像的置乱、替代和扩散完成加密操作。最初的图像置乱大多基于Arnold 变换、幻方变换等，近些年，提出了一些结合混沌理论的空间域图像加密算法[1,2]，由于其密钥敏感性和置乱特性强使这类算法具有较高的研究价值和重要的研究意义。变换域加密算法则从图像变换矩阵的特征出发，使用密钥生成新的变换矩阵对图像进行变换，从而将原本清晰可辨的图像变成类似于随机噪声信息，这种加密方法具有加密效率较高、抗干扰性好的特点，而且便于压缩实现。目前，常用的图像变换包括傅里叶变换[3]、小波变换[4]、离散余弦变换（DCT）[5]等。此外，随着量子信息理论的逐步建立和发展，结合量子信息的优点使量子图像处理超越经典图像处理的局限也是人们努力的方向，量子图像加密[6～9]也逐渐成为研究的热点方向。但是因为量子图像加密中涉及的诸多问题尚未解决，例如量子图像的有效表示、量子图像的完备变换集合以及量子图像安全的信息论模型等，量子图像加密有待进一步深入研究。

本文采用的分数阶变换[10～12]是对传统图像变换的推广，因其具有分数阶敏感性而被引入图像加密领域[13～15]。目前，基于分数阶傅里叶变换的数字图像加密算法的研究很多[16～20]，例如Unnikrishnan等[20]提出了双随机相位编码方案，使用2种独立的随机相位掩模来把图像加密成平稳白噪声；Joshi等[21]提出了傅里叶变换、径向希尔伯特变换相结合的图像加密算法；Lang等[22]提出了基于多参数离散分数存储变换和混沌的图像加密算法。这些图像加密算法有一个很大的局限就是加密后的图像是复值图像，同时包含了幅值和相位信息，非常不利于传输和存储。尤其是随着人们对实时传输的要求越来越高，提出一种满足实数变换、加密安全性高、抗噪性强、计算速度快的图像加密技术非常有必要。

近些年，有学者提出了基于实数域分数阶图像变换的加密方法，如基于保实分数离散余弦变换的图像加密算法[23,24]满足了实数变换的要求，显示出良好的加密效果。离散切比雪夫变换（DTT，discrete Tchebichef transform）是近些年提出的一种新的图像变换技术，其变换核函数由不同阶数的离散切比雪夫正交多项式组成，具有实数域变换、快速迭代计算和良好的图像重建能力[25,26]等特性。相比于许多经典的图像变换，它还具有计算时间复杂度低、便于整数实现等优点，在图像处理中应用得越来越广泛。本文在将DTT推广到分数阶（FrDTT, fractional DTT）的基础上，首次提出基于多阶分数离散切比雪夫变换（MFrDTT）和产生序列（GS, generating sequence）的图像加密方法，使用随机生成的行列分数阶向量替换单一分数阶，结合二维Logistic混沌序列生成的产生序列对图像做2次分数阶离散切比雪夫变换进行加密。多参数分数阶离散切比雪夫变换可以保证实值输入、实值输出。同时，引入的混沌序列对初始值和系统参数高度敏感，GS作为密钥使用，进一步扩展了加密算法的密钥空间，提高了算法的安全性。

2 离散切比雪夫变换

离散切比雪夫变换是由Mukundan等[27]在2001年提出的一种新的图像变换技术，它由不同阶数的离散切比雪夫正交多项式组成，具有快速迭代计算、较高的去相关性、无数值近似和极强的图像重构能力等优点，被广泛应用于图像分析、识别与压缩中[28～31]。n阶离散切比雪夫多项式定义为

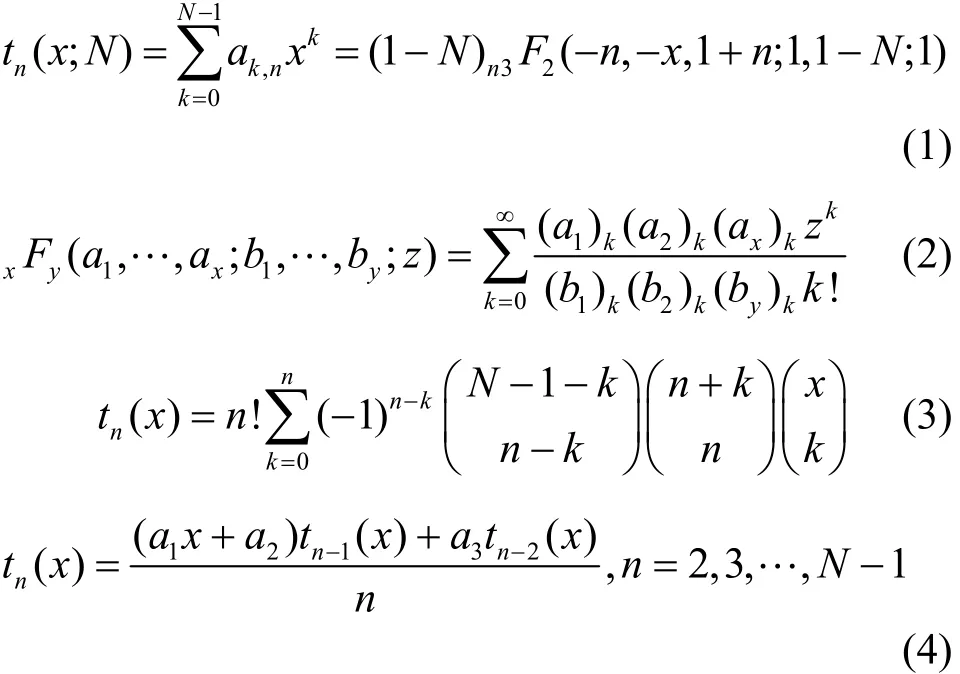
其中，n,x=0,1,2,…,N−1, 超函数xFy定义为式(2)。表示阶乘幂。离散切比雪夫多项式还可以写成式(3)。另外，它还可以通过递推式(4)进行计算。其中

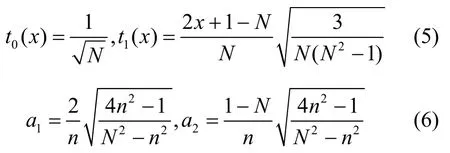
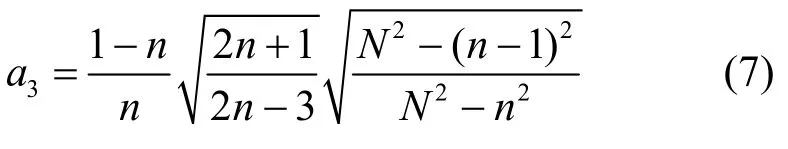
归一化的0～5阶离散切比雪夫多项式变换曲线如图1所示。

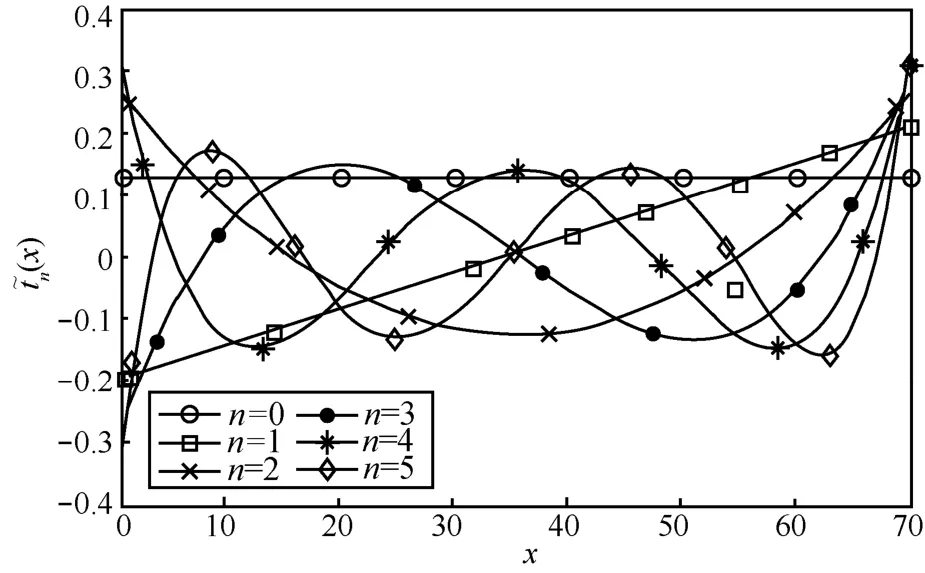
图1 归一化的0～5阶离散切比雪夫多项式变换曲线

对于数字图像f(i,j)，它的DTT可以定义为

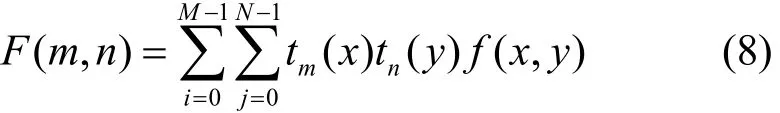
其中，m= 0,1,… ,M−1;n= 0,1,… ,N−1。对应的离散切比雪夫反变换（iDTT, inverse DTT）为

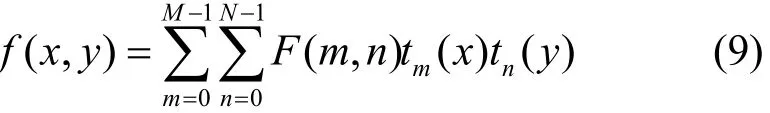
其中，x= 0,1,… ,M−1;y= 0,1,… ,N−1。在实际应用中，图像的DTT可以用矩阵表示为

相应的反变换（iDTT）为

其中，C为DTT矩阵，且CT=C−1。对于典型的8×8的DTT矩阵C，有

3 多阶分数离散切比雪夫变换

FrDTT是对传统 DTT的推广。对于大小为N×N的DTT矩阵C，它满足3个性质：1) 实数矩阵；2) 正交矩阵；3) 酉矩阵。酉矩阵的特性使C的特征值λk分布在单位圆上，即（ϕ是k实数）。

对 DTT矩阵进行特征值分解，得到对应特征值矩阵D以及特征向量矩阵V，满足

其中，V是酉矩阵，由C的N个特征向量un构成，是V的共轭转置矩阵，满足，D是对角线为特征值kλ的对角矩阵。

为了得到同样满足实矩阵、正交矩阵、酉矩阵这3个特性的FrDTT矩阵，本文在矩阵特征分解的基础上把特征值替换成它的α次方（α∈R），即对角矩阵V被它的α次幂代替，从而得出FrDTT矩阵Cα的定义式为

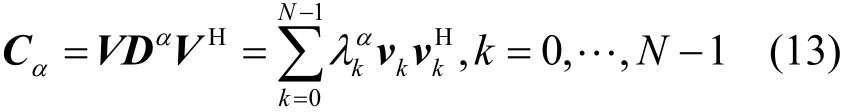
可以证明，Cα同样满足正交性以及指数可加性，即

实际上，矩阵Cα的特征值构成共轭对，设1μ和分别表示特征值1和−1的多重性，根据特征值的分布，可以将其写为

其中，V1和V−1分别是1μ个特征值为1以及μ−1个特征值为−1的矩阵Un的和。值得一提的是，α是非自然数时，是复数，从而矩阵Cα也是复数矩阵。为了得到总是满足实数矩阵的FrDTT矩阵，矩阵的特征值应不包含±1。相较于DCT在矩阵维度信号长度N是4的倍数时才满足不含特征值±1，DTT具有一定的优势，它满足在矩阵维度为偶数时，即N=2N0时不包含特征值±1，在实际应用中更加灵活方便。

进一步地，如果将单一分数阶α扩展到分数阶向量，可以得到多阶分数离散切比雪夫变换（MFrDTT, multiple fractional DTT）的定义式为

接下来，引入产生序列的概念，因为 DTT的特征向量基是唯一的，所以MFrDTT的不唯一性主要取决于特征值的实数次幂，又因为λ= ejϕn，所

k

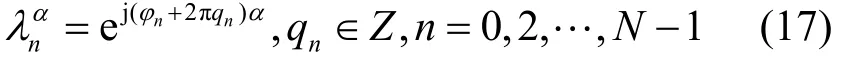
以λnα的取值可以表示为其中，qn是任意的整数，而序列称为MFrDTT的产生序列（GS），不同的产生序列和不同的分数阶将会产生不同的变换矩阵，从而可以应用到图像加密中来。

由式(14)可知，Cα的逆矩阵可以通过它的负阶数矩阵C−α求得。用p表示分数阶，则对于图像f(x,y)，它的二维FrDTT的定义可以表示为

进一步地，将分数阶p推广到多阶分数向量p，可以得到二维MFrDTT的定义为

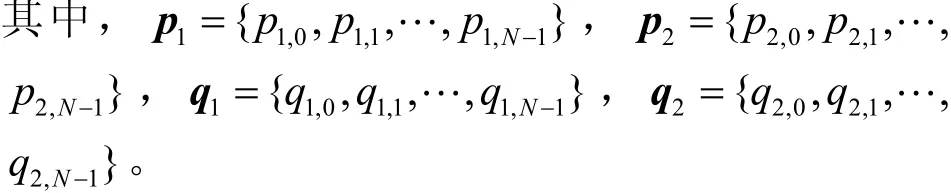
4 图像加密应用

4.1 二维Logistic映射与GS

混沌系统是一种非线性确定性系统，具有非周期性、对系统参数高度敏感性以及序列长期不可预测性等特点，在加密中经常被用来生成随机序列。本文选择具有较多初始值及系统参数的二维Logistic映射得到混沌序列，进而生成分数阶离散Tchebichef矩阵中的GS序列，其迭代式为

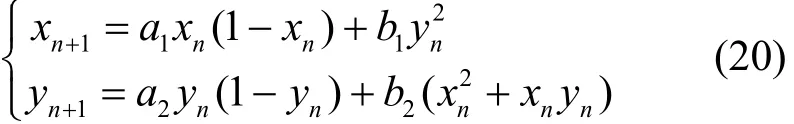
其中，a1、a2、b1、b2是系统参数，xn,yn∈(0,1)，n= 0,1,2…是随机迭代值，x0、y0是初始值。由于b1、b2的取值范围有限，本文不将其作为密钥，实验中设定b1= 0.18、b2= 0.14，其他系统参数和初始值作为密钥使用，分别设定为a1= 3.12、b1=3.34、x0= 0.678 4、y0= 0.789 4。通过式(20)迭代次分别得到2个随机序列，长度为的产生序列和长度为的产生序列

4.2 加解密算法

综上所述，不同的分数阶和产生序列会生成不同的MFrDTT矩阵，这样的特性可以很好地应用到图像加密中。本节介绍一种新的基于MFrDTT的图像加密方法并给出加解密过程的详细步骤。对于一幅大小为M×N的图像，整体加解密过程如图2所示。加密流程的详细步骤如算法1所述。解密过程就是对加密过程的逆变换，基于MFrDTT满足指数可加性，选取分数阶p1′ =−p1，p2′ =−p2即可，图像的解密算法步骤如算法2所示。

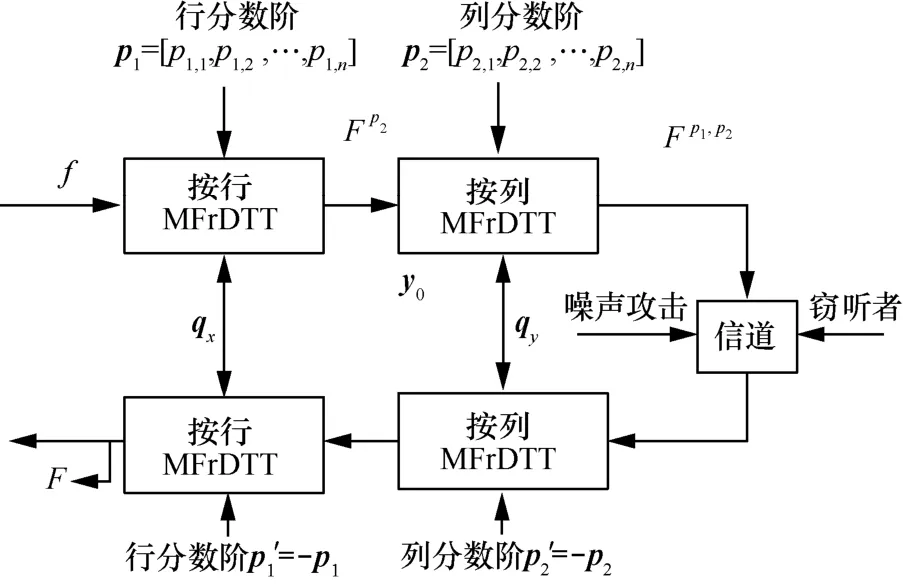
图2 基于MFrDTT和产生序列的图像加解密流程

算法1 MFrDTT图像加密算法

输入 原始图像f

输出 经过MFrDTT加密后的图像F

步骤1 利用随机数产生（0,1）之间互不相关的2个随机数序列qx和qy，长度分别为由于产生序列必须为整数，算法选择将序列中大于0.5的统一设为1，否则统一设为0。

步骤2 为简化选择范围，本文在（0,3）的分数阶范围内，利用随机数生成M维行向量和N维列向量分别对应式(1)中的生成序列qx、qy。

步骤3 对图像f的第i(i= 0,1,… ,M− 1)行进行一维 MFrDTT，变换的分数阶为p1=[p1,1,，对应的生成序列为qx，变换后的图像为F1。

步骤4 对图像f的第j(j= 0,1,… ,N−1) 列进行一维 MFrDTT，变换的分数阶为对应的生成序列为qy，变换后的图像为F2。F2即为加密后的图像。

算法2 MFrDTT图像解密算法

输入 MFrDTT加密后的图像F

输出 解密后的图像f

步骤1 利用加密过程中的产生序列qx、qy，分数阶p1′ =−p1、p2′ =−p2得到MFrDTT矩阵。

步骤2 对加密后的图像F2的第j(j=0, 1,…,N− 1)列进行MFrDTT，分数阶为p2，产生序列为qy，变换后的图像为F1′。

步骤 3 对图像1F′的第 (0,1, , 1)i…M− 行继续进行MFrDTT，分数阶为p1，产生序列为qx，变换后的图像为f′，即解密后的图像。

为了解密出原始图像，必须获得正确的密钥。本文使用 256像素×256像素大小的“Lena”和“Peppers”作为输入图像，如图3所示。加密后的图像如图4所示。从图4可以看出，加密后的图像无法辨认出原始图像的任何信息，这表明原始图像的信息被成功地保护起来。

图3 原始图像

图4 MFrDTT加密后的图像

在解密实验中，本文首先使用正确的密钥来解密，解密后的图像“Lena”“Peppers”分别如图5(a)和图5(b)所示，可以看出，正确密钥成功恢复出原始图像。作为对比，本文使用错误的分数阶密钥p′x、p′y来解密，其中，p′x=px+δ，p′y=py+δ，δ= {0.06}为偏差。解密后的图像“Lena”“Peppers”分别如图5(c)和图5(d)所示。可以看到，通过错误密钥解密后的图像已经完全无法辨认，不能获得原始图像的任何信息，从而保护了原始图像的安全。

图5 使用MFrDTT解密后的图像

4.3 统计分析

图像的灰度直方图是图像分析中的另一项重要特征，它反映了不同图像的不同灰度值分布情况。图6和图7是原始图像和密文图像的灰度直方图。从实验结果可以看出，本文提出的基于MFrDTT的加密方法对这2种图像加密后得到的密文图像灰度直方图非常相似。另外，它们和原始图像的灰度直方图又有很大差异。大量实验后得出一致的结果，图像经过加密后，灰度直方图发生了巨大的变化，不同图像加密后的密文图像的灰度直方图又具有相似的直方图分布。经分析可知，本文提出的基于 MFrDTT的图像加密算法不仅非常好地隐藏了图像的原始信息，同时可以抵抗统计攻击。

图6 原始图像的灰度直方图

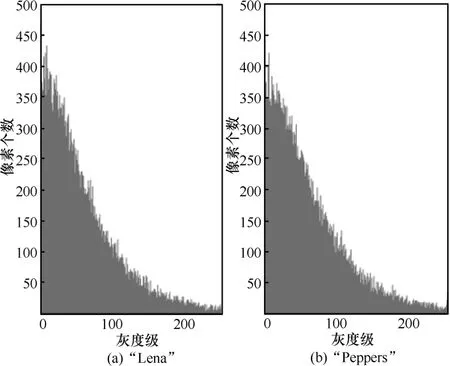
图7 密文图像的灰度直方图

通常情况下，图像的相邻像素之间具有很高的相关性，攻击者很容易通过像素相关性获取整幅图像。为了检验本文提出的基于MFrDTT方法加密后得到的密文图像的去相关性，随机从原始图像和密文图像的水平方向、垂直方向以及对角线方向选取1 000对相邻像素作为样本，计算 3个方向的相关系数，图8是加密前后“Lena”图像在垂直方向上相邻像素间的相关性分析，可以看出，原始图像具有很高的相关性，密文图像则找不出任何规律。进一步地，表1列出了3个方向上的相关系数。从表1可以看出，原始图像3个方向上相邻像素的相关系数接近1，而密文图像的相关系数却近似为0，这说明所提加密算法很好地降低了像素间的相关性，可以抵抗利用图像相关性的攻击。

图8 “Lena”图像加密前后图像垂直方向上相邻像素相关性分析

表1 原始图像“Lena”和密文图像在不同方向上相邻像素的相关系数

4.4 敏感性分析

因为GS是由二维Logistic混沌序列生成，在解密行列分数阶均正确的前提下，实验改变二维Logistic混沌映射的初始值和系统参数，测试其作为密钥的敏感性，实验结果如图9所示。

图9 不同条件下的解密图像

从图9可以看出，即使将初始值和系统参数的偏差调小至 10−15，仍然无法从解密的图像中获得任何有用信息。为了进一步验证密钥的敏感性，本文通过解密图像与原始图像间的均方误差（MSE）进行定量分析，MSE的计算式为

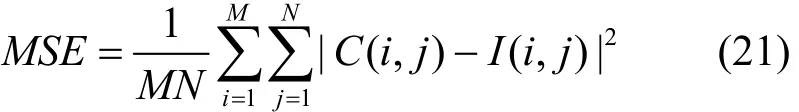
其中，C(i,j)为解密图像灰度值，I(i,j)为原始图像灰度值。实验中通过对系统参数和初始值分别加上偏差δ，计算其对MSE的影响，结果如图10所示。

可以看到，当偏差δ不为0时，MSE非常大，达到4

10的数量级，进一步说明了即使是存在极小的误差，解密图像也依然无法得到原始图像的任何信息。而当偏差δ=0时，MSE接近于0，说明正确的密钥下解密的图像与原始图像几乎相同。因此可以得出通过二维Logistic控制生成GS进行加密具有非常高的安全性的结论。

4.5 密钥空间分析

本文提出的图像加密方法以多参数分数阶p1、p2和二维Logistic混沌映射的初始值和系统参数为密钥对图像进行加密，不同的分数阶和不同混沌映射生成的产生序列组合下的特征值λ不同，从而使变换矩阵Cα不同。通常情况下，安全加密系统的密钥空间应该要大于2100，本文首先利用平均绝对误差（MAE）来分析混沌序列的密钥空间，定义为

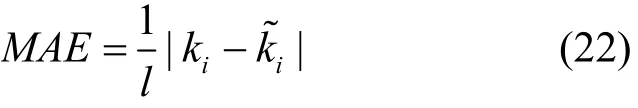
其中，ki、分别是二维 Logistic混沌序列的第i个值，l是混沌序列的长度。当MAE=0时，d的值记为d0，相应的密钥空间就是，4.3节的实验中，d0的值（初始值和系统参数）分别为 3.25× 10−17、1.58× 10−17、 2.13× 10−16、 1.86× 10−16，综合来看，密钥空间为 4.92× 1064，另外，分数阶定义在实数域，也具有海量密钥空间，所以本文所提加密方法足以抵抗计算机穷举攻击。

图10 混沌映射中不同初始值和系统参数误差下的MSE曲线

目前，大部分的图像加密算法的主要密钥包括分数阶和随机相位和振幅掩模，虽然密钥空间很大，但是随机相位和振幅掩模的大小与原始图像的大小相同，对于大量图像加密而言，数据量过大，给密钥的传输带来了很大不便。本文所提方法行列密钥的长度只有相应变换矩阵行列长度的一半，只占用较小的存储空间，Logistic序列只需存储初始值和系统参数，非常利于传输和存储。

5 与其他图像加密算法的分析比较

由于 DCT在图像压缩领域的广泛应用，基于MFrDCT的图像加密研究有很多。DTT与DCT具有相似的变换矩阵，但是 DTT具有更高的能量紧致性、迭代计算速度更快等优点。因为基于MFrDCT与MFrDTT的加密方法同样满足保实变换，本文主要在与MFrDCT对比的基础上，从几个方面与经典的分数阶图像加密算法进行了对比分析。

5.1 分数阶变换时间复杂度

对于不同图像加密中使用的不同分数阶变换矩阵，其生成的时间复杂度是不同的。本文首先从时间复杂度入手分析多种加密方法中分数阶变换性能。实验中使用不同尺寸的“Lena”图像，在主频为3.5 GHz的Intel i5处理器，内存为16 GB，操作系统为Windows 7的计算机中运行Matlab 2014b并统计时间。实验中为了产生2个图像变换矩阵，分数阶向量a使用随机函数在0.4～0.6产生，分数阶向量b使用随机函数在0.5～0.8产生，具体的时间统计如表2所示。

从表2可以看出，基于离散Tchebichef多项式的快速迭代性，MFrDTT在不同分数阶变换矩阵的生成中用时最短，相对其他几种变换具有优势，这在处理大量数据加密时可以节省宝贵的时间。

5.2 解密图像质量

实验中首先选取 5组大小同为 256像素×256像素的测试图像，在正确密钥下进行解密，计算PSNR值。表3分别展示了5组图像用MFrDTT和MFrDTT进行加密再解密后的PSNR值。从表3可以看出，2种算法均有较好的解密效果。由实际计算可知，虽然两者解密后的图像均可取得较高的PSNR值，但本文提出的基于MFrDTT的图像加密算法还是在各组测试图像中略胜一筹，解密的图像质量要优于MFrDCT。

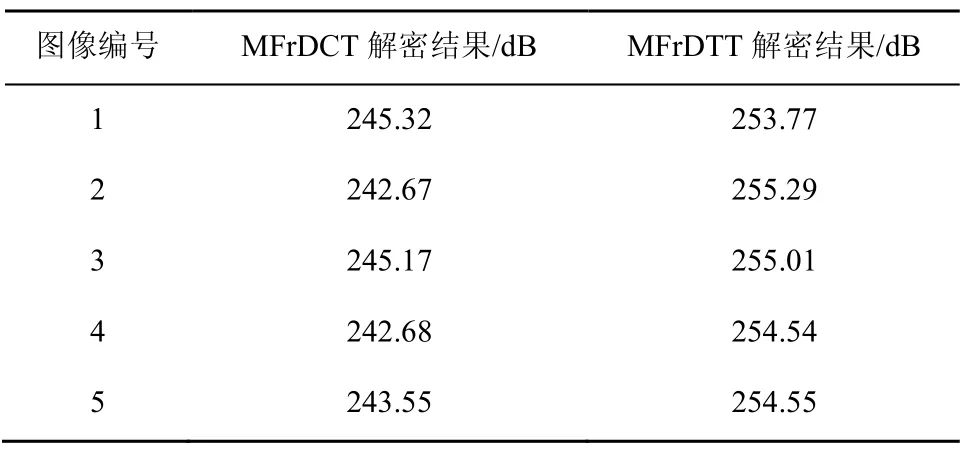
表3 MFrDTT与MFrDCT对多组图像解密后的PSNR

5.3 抗噪声性能

由于图像在传输过程中很容易受到噪声的干扰，这样会影响解密图像的质量。所以衡量一个图像加密方法的好坏应当验证它的抗噪声能力。本文选取均值为 0、方差为 1的高斯白噪声通过式(23)加入“Lena”的密文图像进行噪声干扰。其中，A和A′是密文图像和加噪后的密文图像，k是嵌入强度。通过正确密钥进行解密得到解密图像，计算解密图像的峰值信噪。图11分别给出了本文提出的方法加密后的图像在高斯噪声强度k为0.05、0.10、0.20、0.50、0.80、1.00时的正确解密图像。

从图11可以看出，虽然随着密文中所加的高斯噪声的强度增强，解密后的图像质量逐渐下降，但是当噪声强度为0.10时，图像清晰可见，即使强度增加到 1.00，依然可以依稀辨认出原始图像信息，由此可见，本文提出的加密方法具有良好的抗噪声性能。

为了进一步和当前的经典分数阶图像加密方法对比，实验分别计算了在不同强度噪声下MFrDCT、MFrDFT、MFrDTT解密后图像的PSNR值，如表4所示。从表4可以看出，虽然在噪声强度为0.80和1.00时，MFrDFT解密图像PSNR值更高，但是本文提出的基于MFrDTT的图像加密方法在多数情况下都要优于另外两者，具有较好的顽健性。

表2 不同分数阶变换矩阵的计算时间对比

图11 加不同强度高斯噪声后的解密图像

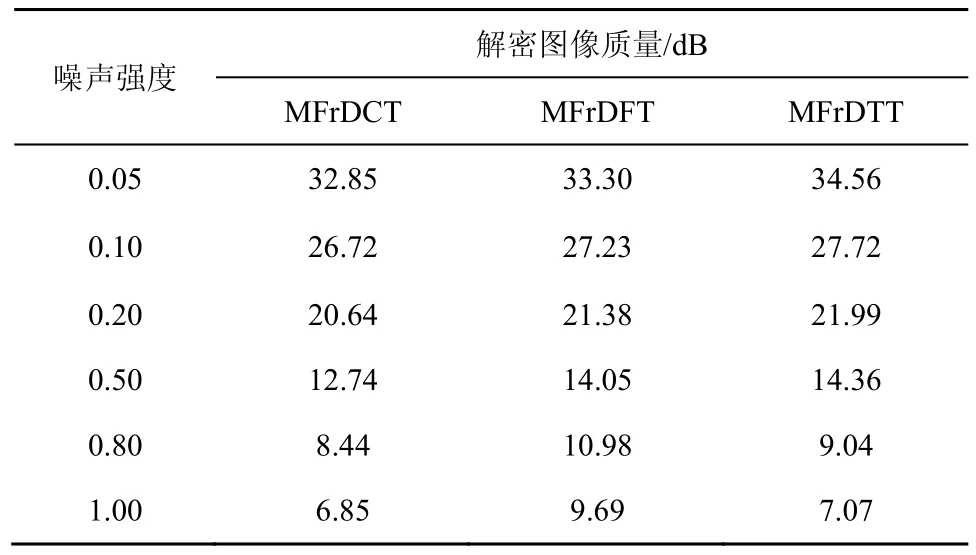
表4 MFrDCT和MFrDTT加密的“Lena”在不同强度高斯噪声干扰后的解密图像质量

6 结束语

本文在定义了分数阶离散切比雪夫变换的基础上，首次提出一种基于多阶分数离散切比雪夫变换和产生序列的图像加密方法，并详细介绍了该加密方法的步骤、特点和实验结果。本文所提方法将切比雪夫变换的分数阶扩展至实数域的分数阶向量，另外，使用二维Logistic混沌映射生成产生序列，增加了图像加密的密钥空间，同时具有很高的密钥敏感性。加密得到的密文图像是实值图像，其大小与原始图像大小相同，方便显示、传输和存储。实验结果表明，该加密算法能够抵抗统计攻击、穷举攻击、相关性攻击等各种图像攻击，具有很高的安全性。因此，本文提出的图像加密方法可以在图像加密通信领域有很好的应用场景。

[1] 文昌辞, 王沁, 黄付敏, 等. 基于仿射和复合混沌的图像自适应加密算法[J]. 通信学报, 2012, 33(11)∶119-127.WEN C C, WANG Q, HUANG F M, et al. Image adaptive encryption algorithm based on affine and compound Chaos[J]. Journal on Communications, 2012, 33(11)∶119-127.

[2] 邓晓衡, 廖春龙, 朱从旭,等. 像素位置与比特双重置乱的图像混沌加密算法[J]. 通信学报, 2014, 35(3)∶216-223.DENG X H, LIAO C L, ZHU C X, et al. Image Chaos encryption algorithm with double displacement of pixel positions and bits [J].Journal on Communications, 2014, 35(3)∶216-223.

[3] CATTERMOLE K W. The Fourier transform and its applications[J].Electronics & Power, 2009, 11(10)∶357.

[4] ANTONINI M, BARLAUD M, MATHIEU P, et al. Image coding using wavelet transform[J]. IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society, 1992, 1(2)∶205-20.

[5] AHMED N, NATARAJAN T, RAO K R. Discrete cosine transform[J].IEEE Transactions on Computers, 2006, C-23(1)∶90-93.

[6] KOMNINOS N, MANTAS G. PEA∶ polymorphic encryption algorithm based on quantum computation[J]. International Journal of Systems Control & Communications, 2011, 3(3)∶1-18.

[7] AKHSHANI A, AKHAVAN A, LIM S C, et al. An image encryption scheme based on quantum logistic map[J]. Communications in Nonlinear Science & Numerical Simulation, 2012, 17(12)∶4653-4661.

[8] EL-LATIF A A A, LI L, WANG N, et al. A new approach to chaotic image encryption based on quantum chaotic system, exploiting color spaces[J]. Signal Processing, 2013, 93(11)∶2986-3000.

[9] YANG Y G, XIA J, JIA X, et al. Novel image encryption/decryption based on quantum Fourier transform and double phase encoding[J].Quantum Information Processing, 2013, 12(11)∶3477-3493.

[10] CANDAN C, KUTAY M A, OZAKTAS H M. The discrete fractional Fourier transform[C]//IEEE International Conference on Acoustics,Speech, and Signal Processing.1999∶1713-1716 .

[11] CARIOLARO G, ERSEGHE T, KRANIAUSKAS P. The fractional discrete cosine transform[J]. IEEE Transactions on Signal Processing,2002, 50(4)∶902-911.

[12] LIU X, HAN G, WU J, et al. Fractional Krawtchouk transform with an application to image watermarking[J]. IEEE Transactions on Signal Processing, 2017, PP(99)∶1.

[13] 陶然, 邓兵, 王越. 分数阶 FOURIER变换在信号处理领域的研究进展[J]. 中国科学 信息科学∶中国科学, 2006, 36(2)∶113-136.TAO R, DENG B, WANG Y. Research progress in fractional Fourier transform in signal processing [J]. Science China Information Science∶Science China, 2006, 36 (2)∶ 113-136.

[14] KANG X, TAO R, ZHANG F. Multiple-parameter discrete fractional transform and its applications[J]. IEEE Transactions on Signal Processing, 2016, 64(13)∶3402-3417.

[15] LIMA J B, NOVAES L F G. Image encryption based on the fractional Fourier transform over finite fields[J]. Signal Processing, 2014,94(1)∶521-530.

[16] SUI L. Asymmetric double-image encryption method by using iterative phase retrieval algorithm in fractional Fourier transform domain[J]. Optical Engineering, 2014, 53(2)∶026108.

[17] ZHOU N, LIU X, ZHANG Y, et al. Image encryption scheme based on fractional Mellin transform and phase retrieval technique in fractional Fourier domain[J]. Optics & Laser Technology, 2013, 47(4)∶341-346.

[18] TAO R, XIN Y, WANG Y. Double image encryption based on random phase encoding in the fractional Fourier domain[J]. Optics Express,2007, 15(24)∶16067-16079.

[19] REFREGIER P, JAVIDI B. Optical image encryption based on input plane encoding and Fourier plane random encoding[J]. Optics Letters,1995, 20(7)∶767.

[20] UNNIKRISHNAN G, JOSEPH J, SINGH K. Optical encryption by double-random phase encoding in the fractional Fourier domain[J].Optics Letters, 2000, 25(12)∶887.

[21] JOSHI M, SHAKHER C, SINGH K. Fractional Fourier plane image encryption technique using radial hilbert, and jigsaw transform[J]. Optics & Lasers in Engineering, 2010, 48(7-8)∶ 754-759.

[22] LANG J, TAO R, WANG Y. Image encryption based on the multiple-parameter discrete fractional Fourier transform and chaos function[J]. Optics Communications, 2010, 283(10)∶2092-2096.

[23] WU J, GUO F, ZENG P, et al. Image encryption based on a reality-preserving fractional discrete cosine transform and a Chaos-based generating sequence[J]. Journal of Modern Optics, 2013, 60(20)∶1760-1771.

[24] WU J H, ZHANG L, ZHOU N R, et al. Image encryption based on the multiple-order discrete fractional cosine transform[J]. Optics Communications, 2010, 283(9)∶1720-1725.

[25] XIAO B, MA J F, CUI J T. Radial Tchebichef moment invariants for image recognition[J]. Journal of Visual Communication & Image Representation, 2012, 23(2)∶381-386.

[26] DAI X B, SHU H Z, LUO L M, et al. Reconstruction of tomographic images from limited range projections using discrete Radon transform and Tchebichef moments[J]. Pattern Recognition, 2010, 43(3)∶1152-1164.

[27] MUKUNDAN R, ONG S H, LEE P A. Image analysis by Tchebichef moments[J]. IEEE Transactions on Image Processing a Publication of the IEEE Signal Processing Society, 2001, 10(9)∶1357-64.

[28] DENG C, GAO X, LI X, et al. A local Tchebichef moments-based robust image watermarking[J]. Signal Processing, 2009, 89(8)∶1531-1539.

[29] YAP P T, RAVEENDRAN P. Image focus measure based on Chebyshev moments[J]. IEEE Proceedings-Vision, Image and Signal Processing,2004, 151(2)∶128-136.

[30] ZHANG L, QIAN G, XIAO W, et al. Geometric invariant blind image watermarking by invariant Tchebichef moments[J]. Optics Express,2007, 15(5)∶2251.

[31] XIAO B, LU G, ZHANG Y, et al. Lossless image compression based on integer discrete Tchebichef transform[J]. Neurocomputing, 2016,214(C)∶587-593.