基于Workbench薄板面内振动超声直线电机振子仿真研究

林 华，翁志刚，张晓东

（皖西学院 机械与车辆工程学院，安徽 六安 230712）

面内振动模态的直线型超声波电机是超声波电机的一个重要分类，电机的结构也多种多样.它主要是直接利用压电陶瓷的逆压电效应及弹性体的超声振动，通过预压力在振子和动子之间产生摩擦力，把弹性体的微观高频振动直接转化为动子的宏观直线运动，无需转换机构可直接推动动子.具有体积小、结构简单、反应快、位置分辨率高、机电转换效率高等优点，可用于精密直线运动平台等场合[1，2].

南京航空航天大学超声电机工程研究中心成功研制了国内首台基于薄板面内振动的单足型直线电机（图1），以及基于矩形薄板面内振动的双足型直线超声电机（图2）[3，4]，其采用的是矩形金属板和压电陶瓷贴片的复合振子.华侨大学针对双足型矩形压电陶瓷薄板面内振动直线超声电机作了相关的研究制作，采用的压电陶瓷材料的矩形薄板和金属驱动头的复合振子（图 3、图 4）[5，6].

图1 单足型直线超声电机

图2 双足型直线超声电机1

图3 双足型直线超声电机2

图4 双足型直线超声电机3

面内振动直线型超声电机主要是利用矩形薄板第一阶面内伸缩振动L1模态和第二阶面内弯曲振动B2模态来工作（图5、图6），并对矩形薄板进行合理的结构设计可使得这两个振动模态的频率值尽可能相等（即要实现频率一致性要求），这样才能在信号的同一驱动频率下同时激励出这两个面内振动模态，从而实现驱动头的椭圆型运动轨迹，进而实现超声电机的运转.

图5 一阶纵振

图6 二阶弯振

两端边界自由时，面内一阶L1和二阶B2振动频率根据薄板振动理论及经验公式有[3]：

材料的剪切模量；I为矩形截面转动惯量.

为满足频率一致性要求，应尽可能使ωL1=ωB2，解公式（1）和（2）得：L/B≈4.2.现实中由于安装、边界条件等有所变化，会使其频率发生变化，通常取L/B=4.0且是可行的.薄板的定义是厚度值要远小于宽度值，可取2-5mm.固定长宽比的情况下，较小范围内改变厚度对频率一致性影响较小[2]，本文仿真中选取板的厚度均选为3mm.

在实验中对电机振子的固定方式进行分析发现，采用中心孔固定可以简化电机结构，设置双驱足可以有效提高电机输出效果.采用有限元模态仿真研究可以方便地根据要求进行设计和修正.

本文利用Workbench16对共振频率范围在20KHz-50 KHz，长宽比为4，尺寸分别为：80×20×3mm3、60×15×3mm3、40×10×3mm3，材料分别取铜合金、45号钢、PZT，在矩形板中间设计安装螺栓的固定孔、在长边设置双驱动足的矩形薄板进行模态仿真研究，观察孔径大小、驱动足位置对纵振、弯纵频率一致性的影响.

1 不同孔径对矩形薄板频率一致性的影响

图2电机的薄板振子（铜合金）需要通过螺栓等固定在底座上，下面以80×20×3mm3铜合金材料的矩形板为例，暂不设计驱动足，考察不同孔径对矩形薄板频率一致性的影响.在软件环境中设置：弹性模量 110GPa，密度8300kg/m3，泊松比 0.34，边界条件自由，孔处不加约束，进行自动网格划分，单元尺寸1mm，并进行模态分析，搜索20KHz以上频率，得到各阶振型，提取纵振和弯振频率，观察仿真后的模态图（一阶纵振图5和二阶弯振图6），在振型中，几何中心位置的形变量是几乎没有的，为了不影响振型，在板的正中间处设计通孔并予以固定.取中间孔的直径分别为 2mm、3mm、4mm、5mm、6mm，并重新仿真得到φ2-φ6孔径纵弯模态频率差如下表1所示.

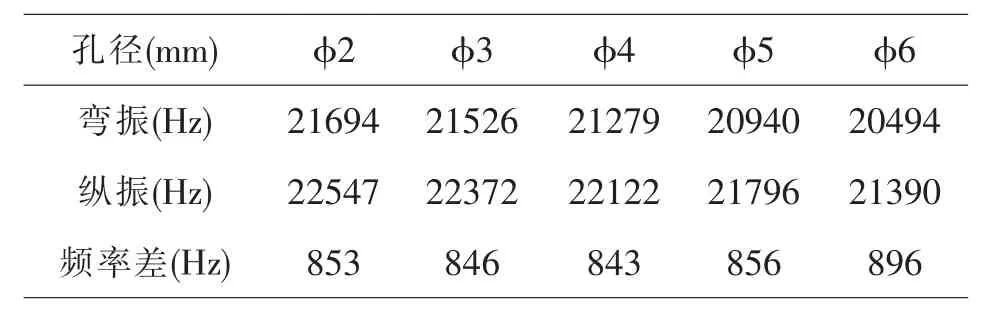
表1 φ2-φ6孔径纵弯模态频率差(Hz)

由上表发现，在长宽厚不动的情况下，孔径的大小变化对模态的频率差影响不明显.其中在φ4mm孔径时纵弯模态频率差最小，所以在孔径φ4-φ5之间细化孔径，按照GB/T5277-1985螺栓和螺钉用通孔尺寸表中精装配、中等装配、粗装配直径选择φ4.3、φ4.5、φ4.8进行再次模态分析，得频率差如下表2所示.

表2 φ4-φ5孔径纵弯模态频率差(Hz)

由上表发现，进行细化孔径研究后，频率差变化微小，相对于20KHz以上几乎可以忽略不计，取孔加工中的中等装配精度φ4.5进行下一步研究，根据电机定子实际安装时条件，固定约束中心孔，进行模态分析，发现弯振频率为22883Hz、纵振频率为23032Hz，二者相差149Hz，相差7‰，基本上满足频率一致要求，其弯曲和纵振模态图如7、8所示.

图7 弯振模态图

图8 纵振模态图

2 双驱动足位置设计

对于薄板面内振动模态的直线型超声波电机的驱动头有两种安装方法，一是安装1个驱动头在宽边的中点处（图1电机），二是安装2个驱动头在长边上（图 2、3、4 电机）.实验表明，双足型的电机有更好的驱动速度及平衡性，但推力会小一些[6].

分析图7的振动模态可知，在弯曲振动模态的波峰与波谷处安装2个驱动头是最佳的，可以获得较好的振动状态及输出特性.观察波峰与波谷位置，出现在离宽边25.5mm处，取3×3×3mm3的驱动头对称安装在离两宽边的24-26mm处.软件环境选择上节相同的参数并重新建模、划分网络、约束中心孔、进行模态分析，图如下所示（图9），得纵振频率为22965 Hz、弯振频率为22768Hz，频率相差197Hz，相差8.6‰，基本上满足频率一致要求.

图9 弯曲振型图

图10 弯曲振型图

观察9图，其驱动头的振动轨迹是理想的，可在波峰与波谷获得最大振幅及推力.

根据图8纵振模态图可知，越靠近宽边处纵振位移越大，为了提高电机直线运动速度，计划把驱动足往宽边移动3mm，对称安装在离两宽边的21-23mm处，所得振型如图10所示.观察图10以及动画，可明显发现驱动足的振动轨迹是斜着的，对于电机输出位移有相互抵消的效果，所以不可取.故可得，驱动足的理想位置与长度的比例是25.5/80= 0.31875.

3 不同材料及孔径的振子频率一致性研究

在矩形薄板面内振动模态直线型超声波电机振子安装双驱动足，并针对其常用的3个尺寸以及3个常用的材料进行仿真分析，寻找最佳孔径尺寸.材料分别取铜合金、45号钢、PZT，尺寸分别取80×20×3mm3、60×15×3mm3、40×10×3mm3.

（1）对80×20×3mm3的振子，驱动头对称安装离两宽边的24-26mm处，按螺栓和螺钉用通孔尺寸标准取不同的中心孔径，进行模态分析，所得纵振与弯振频率差，如下表3所示.

表3 定子的不同孔径及材料时频率差(Hz)

从表中可看出，当孔径与板宽的比例，铜和PZT材料为5/20=0.25，45钢为4.8/20=0.24时，振子纵弯振动频率差最小，频率一致性最好.

（2）对60×15×3mm3的振子按上述结论取驱动足的位置为25.5×60/80=19.125，取3×3×3mm3两个对称安装在离宽边17-19mm处，按标准取不同的中心孔径，进行仿真研究，结果如下表4.

表4 定子的不同孔径及材料时频率差(Hz)

从上表中可得，在频率差最小值处，孔径与板宽的比例，铜和PZT材料为3.9/15=0.25，45钢为3.4/15=0.227.定子弯曲振型如图11所示，可见驱动足的安装位置比例是可取的，刚好正在波峰波谷处.

图11 定子弯曲振型图

图12 定子弯曲振型图

（3）对40×10×3mm3的定子，按标准取不同孔径，并按上述结论的比例取驱动足位置为25.5×40/80=12.75，取3×3×3mm3两个对称安装在离宽边11-13mm处，进行仿真研究，结果如下表5所示.

表5 定子的不同孔径及材料时频率差(Hz)

分析表5数据可得，频率差最小值处，铜和PZT材料孔径与板宽的比例为2.6/10=0.26，而45钢则不能用于该类型电机的该尺寸振子.弯曲振型如图12所示，可见驱动足的安装位置在波峰波谷处是可行的.

4 结论

基于矩形薄板面内振动超声直线电机一阶纵振和二阶弯振频率的一致性要求，利用Workbench16对电机常见的3种尺寸振子进行振动模态研究分析，得出了以下结论，可为同类型电机的结构设计提供参考.

（1）径宽比：在矩形板中间设计用于安装固定的通孔，满足振子材料为铜和PZT时径宽比约在0.25，45钢时径宽比为0.2335，振子的纵弯振频率一致性较好；

（2）驱动足：在矩形板长边对称设计双驱动足，放置在距两侧宽边各25.5/80=0.31875倍处，可使得输出效果最佳；

（3）材料：不同材料对频率一致性影响也各不相同，可根据加工、装配、成本等实际情况合理选择振子材料.在板长为60mm以下时，不建议采用普通结构钢作为振子材料.

〔1〕 时运来，张军，冯森等.一种新型面内模态直线超声电机的驱动机理及试验研究[J].声学与振动，2014（2）：29-37.

〔2〕 陈成都.面内模态直线超声电机结构设计及驱动方法研究[D].哈尔滨：哈尔滨工业大学，2017.

〔3〕 刘剑，赵淳生.基于矩形薄板面内振动的直线型超声电机的研究[J].声学学报，2003，28（1）：86-90.

〔4〕 许海.双足型直线超声电机的原理分析及结构设计[J].机械设计与制造，2007，26（11）：1498-1500.

〔5〕 郑文灿，洪尚任，林华等.纵弯模式驻波超声波直线电机的研制与实验 [J].微电机，2011，44（10）：38-40.

〔6〕 林华，翁志刚，张晓东等.面内模态超声直线电机对比实验研究[J].齐齐哈尔大学学报（自然科学版），2013，29（1）：34-36.