基于T-S模型时滞网络控制系统的保性能H∞鲁棒控制

李 杨，张鸿恺

（安徽建筑大学 电子与信息工程学院，安徽 合肥 230022）

1 引言

随着网络控制系统(NCS)在工业控制过程、航天航空和智能建筑控制等方面的广泛运用，NCS的分析与设计已逐渐成为当代控制理论的研究热点之一[1-4].文献[1]针对一类具有积分二次约束属性的时滞网络控制系统，研究了其H∞鲁棒容错控制.文献[2]研究了具有状态观测器时滞的网络控制系统的鲁棒H∞控制问题.文献[3]考虑控制器存在扰动情况下，进一步研究了带有状态观测器的网络控制系统非脆弱H∞控制问题.

自1985年Takagi等[5]提出T-S模糊模型以来，基于该模型的方法被广泛应用到研究非线性系统稳定性分析和控制综合中[6-9].文献[6]首先对于模糊时滞系统的稳定性分析和控制综合进行了研究.文献[7]针对一类具有参数不确定的T-S模糊系统，研究了其鲁棒H∞控制问题.文献[8]针对一类基于T-S模糊模型描述的连续非线性网络控制系统，研究了其基于观测器的鲁棒L2-L∞控制器设计问题.

本文考虑在外界噪声输入下的一类T-S模糊模型描述的时滞网络控制系统，研究其模糊保性能H∞鲁棒控制问题.首先将NCS建模为具有时变参数的离散时间系统模型.然后通过Lyapunov理论和线性矩阵不等式方法，提出模糊保性能H∞鲁棒控制器的设计方法.

2 问题描述

NCS一般是通过实时网络形成的闭环反馈控制，其基本结构如图1所示.其时滞一般包括传感器到控制器的时延τsc，控制器到执行器的时延τca以及控制器的计算时间τc.令τ=τsc+τc+τca，考虑一类由模糊 T-S模型描述的时滞网络控制系统，其第i条模糊规则为：

图1 NCS的基本结构

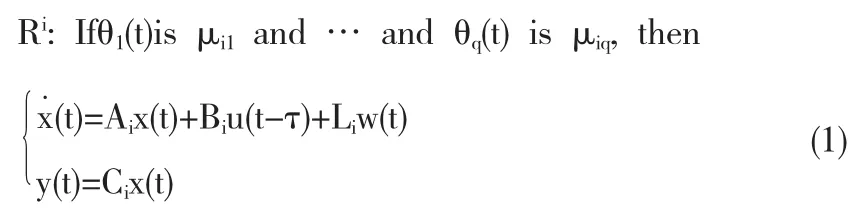
其中：Ri表示T-S模糊模型的第i条规则，m为规则数目，θ1(t),…,θq(t)为规则前件变量，μij为模糊语言值集合；x∈Rn,u∈Rz,y∈Rq和w∈Rr分别为状态、控制、输出和干扰向量；Ai,Bi,Ci,Li是已知的适当维数矩阵.

为便于进一步讨论，先做以下假设：

①在信息传输过程中存在变时滞，时滞有界且不超过采样周期，即τ∈[0,T]，其中T为采样周期.

②传感器采用时间驱动，控制器和执行器节点均采用事件驱动方式.

基于如上假设，在一个采样周期内，系统输入不再是一个单一的常数，而是一个分段常数.在一个采样周期内，控制输入可表示为：

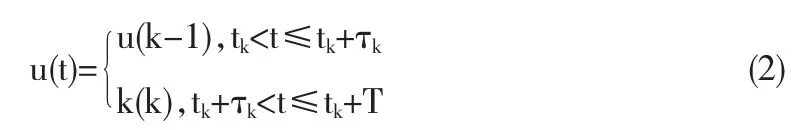
其中Gi是第k个采样时刻，τk是相应的时滞.因此，系统(1)的NCS离散状态空间表达式为：

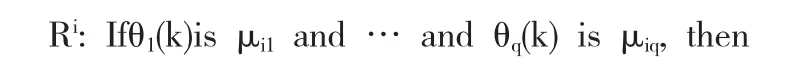
由于不确定时滞τk的存在，H0i和H1i也是时变的.因而，系统（3）含有不确定参数，根据文献[4]可以给出式（3）的等价模型：

其中和E是适当维数的常数

i矩阵,Fi是不确定分量并且满足FiTFi≤I,具体详见文献[4].

采用单点模糊产生器、乘积推理机以及中心模糊消除器，全局模糊控制系统可写成如下形式：

对系统（5）采用如下形式的模糊控制器

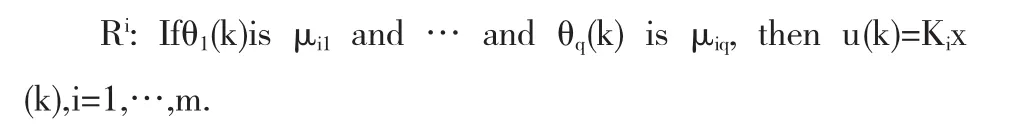
系统(5)全局控制律为：

则闭环系统为

其中S是给定的正定对称矩阵.

本文的目的是设计形如(6)式的控制器，使得对所有允许的参数不确性，以下条件成立：

①在w(k)=0时，式(7)的闭环系统是鲁棒稳定的；且存在性能指标J*，使得相应的闭环性能指标式（8）满足J≤J*.

②在x(0)=0时，对给定的正常数γ，输出y(k)满足||y(k)||2＜γ||w(k)||2.

引理1 给定适当维数的矩阵D，E，及满足FTF≤I的矩阵F，则有对任意的标量ε＞0，使得DFE+ETFTDT≤εDDT+ε-1ETE.

3 主要结果

定理1对于系统(7)，如果存在正定矩阵P，Q和实矩阵Ki，使得下列矩阵不等式成立：

则系统(7)是鲁棒稳定的，且控制器（6）是系统的H∞保性能控制器，相应的性能指标满足：

其中，*表示对称块矩阵，

证明 构造Lyapunov函数如下

①根据不等式（9）、（10）可知当 w(k)=0 时，ΔV(x(k))＜0，所以系统（7）是鲁棒稳定的.且有：

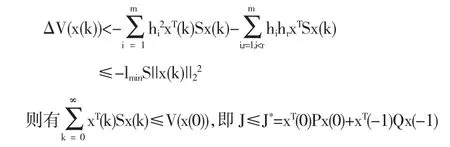
②在0初始条件下，考虑Jk=||y(k)||2-γ2||w(k)||2，对任意w(k)∈L2[0,∞)有

利用矩阵的schur补的性质，由不等式(9)、(10)可得

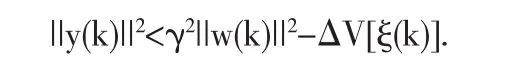
将上式两边对k从0到∞求和，并利用系统的稳定性及0初始条件，可得||y(k)||2＜γ||w(k)||2.

定理得证.

定理2 对给定的系统(7)，如果存在对称正定矩阵X，U和矩阵Wi，Ti以及常数εir＞0，使得下列线性矩阵不等式成立：

则系统(7)稳定，是系统的 H∞保性能控制器，相应的性能指标满足：

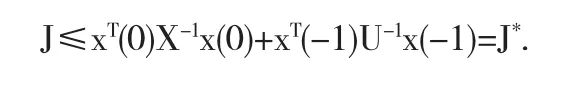
其中，

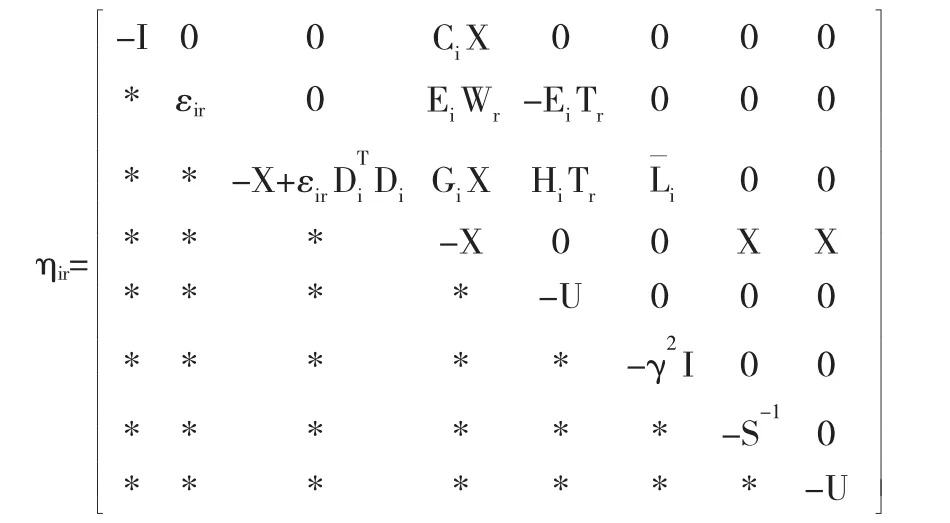
证明 多次利用引理1及矩阵的Schur补性质，式(9)等价于

将(13)式分别左乘和右乘矩阵diag(I,I,I,P-1,Q-1,I,I)，并记X=P-1，U=Q-1，Ti=KiU，Wi=KiX，然后再次应用矩阵的 Schur补性质，可得矩阵不等式(11)，定理得证.同理可证得(12)式.

基于定理2，闭环系统（7）的H∞保性能控制器可通过求解如下最优化问题得到，且系统的性能指标满足J≤J*=α¯+β¯.

4 结论

本文针对一类采用T-S模糊模型表示的时滞网络控制系统，研究了其模糊保性能H∞鲁棒控制问题.运用Lyapunov稳定性理论和LMI方法，给出了模糊保性能H∞鲁棒控制器的存在条件.通过参数变换和矩阵的Schur补性质，以LMI的形式给出了模糊保性能H∞鲁棒控制器的设计方法.最后给出数值例子，对所得结果进行检验，仿真表明本文提出的算法是有效的.

〔1〕 彭高丰,蒋伟进.具有积分二次约束属性的网络控制系统H∞容错控制[J].控制理论与应用,2016,33(3):406-412.

〔2〕 Lijia Liu,Xianli Liu,Chuntao Man,et al.Delayed observer-based H∞control for networked control systems[J].Neurocomputing,2016(179):101-109.

〔3〕 周颖,郑凤,何磊.具有时变时延和丢包的网络控制系统H∞控制[J].计算机技术与发展,2017,27(5):164-169.

〔4〕 谢成祥,樊卫华,胡维礼.一类短时延网络控制系统的建模和控制方法[J].南京理工大学学报(自然科学版),2209,33(2):156-160.

〔5〕 Takagi T,Sugeno M.Fuzzy identification of systems

and its applications to modeling and Control[J].IEEE

Trans on Systems,Man&ybernetics,1985,15(1):387-403.〔6〕Márquez R,Guerra T M,Bernal M,et al.A nonquadratic Lyapunov functional for H∞control of nonlinear systems via takagi-sugeno models[J].J of the Franklin nstitute,2016,353(4):781-796.

〔7〕 陈珺,贺铁清,刘飞.基于非二次 Lyapunov函数的不确定模糊系统鲁棒H∞控制[J].控制与决策,2017,32(12):2247-2253.

〔8〕 李艳辉,吴迪.考虑随机时滞的非线性网控系统鲁棒L2–L∞控制[J].控制理论与应用,2017,34(7):931-937.

〔9〕 Kchaou M,Hajjaji A E,Toumi A.Non-fragile H∞outputfeedback controldesign forcontinuoustime fuzzy systems[J].Isa Transactions,2015,54:3-14.