再议高等数学中数列极限的求解

李庆娟

（大连财经学院 基础教育学院，辽宁 大连 116600）

极限的思想、概念与方法是分析数学问题的基本工具和语言，它是高等数学的重要理论基础，贯穿于高等数学教学的始终，高等数学中很多重要的概念都是通过极限来定义的.关于极限的求解主要有两方面，一是数列极限求解问题，二是函数极限求解问题，二者有相通之处.但相对而言，前者是培养和训练极限思维的基础，后者是更为深入研究极限的思维方法，掌握好数列极限的思想以及求解方法是有助于高等数学的后期学习的.下面主要是讨论一下数列极限的主要计算方法与技巧.

1 利用定义验证法求证数列极限

一般地，利用定义法验证数列极限，往往是事先知道极限存在且知道极限值的，在验证过程中，关键是通过分析定义法，将定义中的大N找到，这个正整数N是与ε有关的，找到大N之后，再按照定义完整的叙述一遍定义，证明过程就完成了.但值得一提的是定义验证法对于初学者来讲非常有难度，很多学生很难理解，其实要想熟练掌握数列定义验证法，关键之处就是一定要充分理解数列极限的定义，只有充分理解定义，我们在验证极限时才能得心应手.

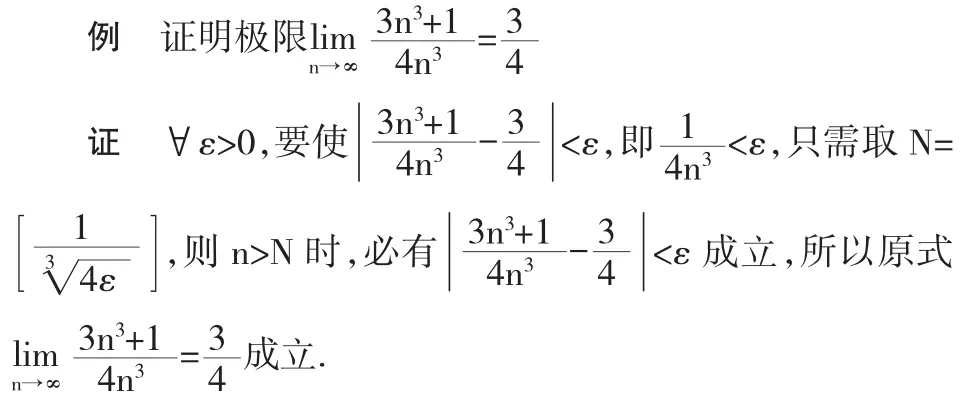
2 通过变形、化简等方法求解数列极限

在求解数列极限时，有时需要对数列的通项表达式做适当的恒等变形，如有理化、通分、拆分等方法，在利用这些方法求解数列极限时，一般都要结合数列极限的四则运算法则.但应该注意的是四则运算法则可以推广到有限个数列上去，不能推广到无限个数列或是不定个数列的情形上.

3 利用夹逼定理求解数列极限

夹逼定理是计算数列极限的主要方法之一，利用夹逼定理时，关键之处是要将给定的数列进行适当地放缩，放缩后的两个数列极限要都存在且相等，从而利用夹逼定理进行判断并求解出给定数列的极限.

4 利用单调有界准则求解数列极限

单调递增且有上界的数列必存在极限，单调递减且有下界的数列必有极限.单调有界数列必有极限准则是证明和计算数列极限非常重要的方法.

5 利用重要极限求解数列极限

在函数极限理论中有两个重要极限，利用它们计算相应函数极限是非常典型并且也是常用的方法，那么计算数列极限时，也可以套用此方法，应用此方法时必须注意两个重要极限的形式和特点，只有把要求解的极限化简或变形为与重要极限形式一致才行.

6 利用无穷小性质求解数列极限

在微积分学习中，我们知道无穷小有很多重要性质，其中无穷小量与有界数列（或有界函数）的乘积仍然是无穷小量，这个性质经常用来求解相应的一类极限问题.

在该例中，我们注意到cos(5n+1)，(n→∞)时极限显然不存在，但是它是一个有界的数列，而)时又是无穷小量，根据无穷小的性质可知，原数列极限存在且为零.

7 利用不定积分定义求解数列极限

定积分的概念是通过极限定义的，它是一个特定和式的极限问题，在实际问题中有着非常广泛的应用.所以遇到特殊和式的极限问题或是可以转化成这种结构的极限，就可以将其转化成定积分，从而求出极限值，这也是求解数列极限非常重要的一种方法.

解 首先变形，将极限式化成符合定积分的特殊和式极限问题

8 利用级数收敛的必要性求解数列极限

利用级数的必要性求解数列极限具有一定的局限性，它只能求解极限为零的数列极限问题，但是方法比较典型.

解 利用达朗贝尔判别法：

9 利用等价无穷小替换求解数列极限

在求解数列极限时，我们可以利用求函数极限的典型方法求解，即等价无求小替换的方法.常用的等价无穷小有：

此外，还可以利用中值定理求解数列极限，常用的中值定理指的是拉格朗日中值定理和积分中值定理.

再有，就是利用泰勒公式求解数列极限，主要用的是带佩亚诺余项的泰勒公式，常用的公式有七个，在此就不一一列举了.

以上主要是介绍了高等数学中求解数列极限的几种主要方法与技巧，这些方法都是在求解极限经时经常会用到的方法和技巧，需要我们熟练掌握，当然除了这些方法之外，还有其他方法，比如说柯西准则，Stolz定理等.熟练掌握数列极限的概念、性质和计算是学好微积分的重要前提和基础，在学习的过程中，我们要学会善于总结和归纳，并能够灵活巧妙地应用它，从而无论碰到怎样困难的实际问题都能迎刃而解，并且从真正意义上理解数列极限求解的思维模式以及真谛.

〔1〕 李庆娟.基于高等数学中数列极限求解的讨论[J].佳木斯职业学院学报，2015：245.

〔2〕 张俊青.数列极限求解方法的探讨[J].科技信息，2016：150-151

〔3〕 潘福臣.李庆娟，等.高等数学[M].吉林大学出版社，2014.

〔4〕 吴传生.微积分[M].高等教育出版社，2009.

〔5〕 同济大学应用数学系.高等数学第五版[M].高等教育出版社，2001.