基于双三次插值的巡检机器人初始位姿优化

林 欢，王 锋

(亿嘉和科技股份有限公司，江苏 南京 210012)

目前智能电网的建设过程中需要对变电设备状态进行检测，利用变电站智能巡检机器人能够实现变电站全天候、全方位、全自主的智能巡检和监控，有效降低了工人劳动强度和变电站自身运行维护的成本，提高了巡检机器人正常作业和管理的智能化、自动化水平，为智能变电站提供了创新性的技术检测手段和全方位的安全保障[1]。

与传统的轨道式巡检机器人不同，利用二维激光定位导航的智能巡检机器人[1]不仅可以节省轨道铺设的成本和工作量，而且巡检工作更加灵活，可以根据需要进行巡检路线的规划。巡检机器人在激光定位的工作过程中，机器人的初始定位会影响到整个巡检过程的效率和准确度。初始定位的不准确不仅会增加机器人迷路的可能性，而且对后续设备检测的位置和角度也会产生不良的影响。因此，初始位姿优化方法的设计，是开发变电站自主巡检机器人中的关键技术。

机器人巡检过程中，初始定位与实时定位之间的主要区别在于：实时定位要求在毫秒级别内实现；而初始定位不受时间限制，可以进行更大范围的搜索和优化计算。

目前大部分研究都默认初始位置已知[2]，因此对初始定位的研究较为简单。最初使用2D激光测距雷达将扫描得到的地图和已知地图进行匹配，得到初始定位点，但是该方法计算量大，而且对扫描得到的信息无法进行精确的辨别，导致算法的鲁棒性差，无法适应环境中临时出现的轻微变化。TODD等[2]采用全局求互相关的方法，将当前扫描图与已知地图中相关值最大的位置作为机器人的初始位置，但是该方法同样存在定位不准确、计算量大等问题。项志宇[3]结合激光测距雷达数据的特点，提出了基于“完整线段”匹配的新方法来实现初始定位。只把完整的部分特征与已知地图进行匹配定位，虽然大大降低了计算量，但经常会出现局部匹配不符的情况，从而导致初始定位的不准确。王璐[4]利用隐马尔科夫模型(hidden markov model,HMM)对环境中特殊标记物之间的空间关系进行建模，可以较为有效地匹配相似环境，但无法用于动态环境中。

针对上述问题，本文提出了一种基于双三次插值算法的初始位姿优化方法。该方法考虑了变电站稀疏空旷的实际环境，对激光扫描得到的初始定位估值进行优化，采用双三次插值法来实现优化目标，可以得到最优的初始位姿。本文所提方法采用的硬件系统传感器包括里程计(odometer)、惯性导航单元(IMU)、激光传感器(laser)。软件系统使用机器人操作系统ROS(robot operating system)。在ROS系统下实现一个Car Localization的定位节点，在定位节点启动阶段，使用本文初始位姿优化方法实现变电站智能巡检机器人高精度的初始定位。

1 初始位姿估计

机器人开始巡检工作前，已经构建了变电站的二维环境地图，地图和机器人运动全部假定在一个二维平面内，建立3个坐标系：地图坐标系、机器人坐标系以及激光传感器坐标系。使用ROS系统中TF(transform)模块实现不同坐标系中数据坐标值的转换。巡检机器人的位姿Pose可以表示为P(x,y,r)，其中(x,y)表示机器人在地图坐标系中的位置，r表示机器人的朝向。

1.1 定位窗口扫描

Car Localization定位节点获得当前初始定位初值Ps(x0,y0,r0)的方法有两种：一种是根据上次工作结束时保存在地图文件中的位姿信息来获得；另一种是根据ROS系统/initialpose主题中保存的位姿信息来更新。在获得初始定位初值Ps(x0,y0,r0)、地图数据以及激光数据之后，就可以开始初始位姿的定位窗口扫描[6]，如图1所示。

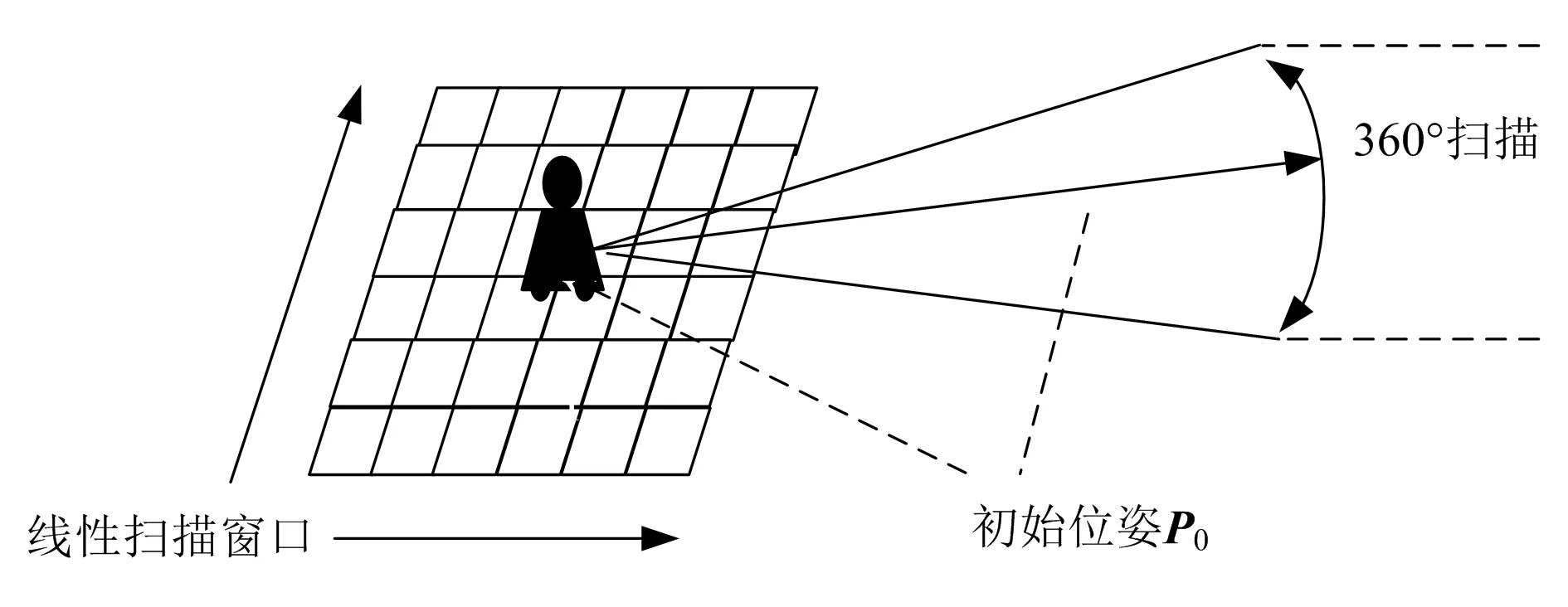
图1 初始定位扫描示意图

由于实时性要求不高，以初值Ps(x0,y0,r0)为中心设定正方形定位扫描窗口，线性范围一般为1m，精度为0.1m×0.1m。角度范围360°，角度步长为1°。每得到一帧符合要求的激光数据(laserscan)的情况下，通过定位窗口的扫描，就可以获得较优的初始位姿估计点Pe(x0,y0,r0)。每帧激光数据会存储N个激光点数据，这些激光点数据经过ROS系统自动处理后会得到相应的激光点云数据(pointcloud)。在定位过程中使用激光点云数据来进行处理和计算，过程如下：

Step1，根据初始定位初值Ps(x0,y0,r0)、激光点云数据和用于ROS系统接口调用的角度扫描参数θwindow，θstep计算各角度的激光点云数据(rotatedcloud)。

Step2，将Ps(x0,y0,r0)设定为预测位置，根据rotatedcloud数据和地图数据计算各角度点云数据中各点对应的地图栅格坐标位置，得到不同角度激光点云数据对应的离散扫描数据。

Step3，根据窗口大小扫描参数和角度扫描参数θwindow，θstep计算定位窗口大小，同时计算出可能的位姿候选ζpossible，从而获得较优的初始位姿估计点Pe(x0,y0,r0)。

1.2 置信度计算

针对变电站空旷稀疏的环境特点，利用激光最小和最大的参数值Lasermin，Lasermax对激光点云数据进行过滤，去掉了数据中相应的噪点，将剩余的激光点数据作为有效点。把每帧激光数据pointcloud中的有效点从N个降低到h个，提高了初始定位估计的置信度。根据系统过滤的结果不同，在每帧激光数据点数据为1 141的传感器上h约为几百的量级[7]。

Step1，根据每个候选位姿ζpossible对应的离散扫描数据中的栅格置信度，计算每个位姿的置信度αcandidate。每个离散扫描数据中有h个栅格，每个栅格的地图坐标为(x,y)，对应的置信度是αxy，置信区间为[0.1～0.9]，根据当前的环境条件进行判断，从而选择相应的置信度αxy的值。

(1)

Step2， 根据每个位姿候选ζpossible与初始位姿估计点Pe(x0,y0,r0)的位姿差来计算每个位姿对应的置信度权重αweight。

αweight=e2q

(2)

(3)

式中：xoffset，yoffset分别为x，y方向坐标；αrotation为位姿旋转方向置信度，其置信区间为[0.1～0.9]。Wtrans，Wrotation分别为位移和旋转权重，其值需根据实际环境条件获得。

Step3，将每个位姿的置信度与置信度权重的乘积作为当前位姿的分值(Score)。

Score=αcandidate·αweight

(4)

Step4,取分值最高的位姿作为初始定位估值Pf(x0,y0,r0)，为了实现最优的初始位姿，本文采用双三次插值法对其进行优化。

2 双三次插值法

根据机器人在地图中的任何一个位姿都可以计算出对应位姿的激光点云数据pointcloud和对应的置信度αpose，从而得到分值最高的初始定位估值。然后对Pf(x0,y0,r0)用双三次插值算法来进行二次非线性优化计算，从而获得最优初始位姿P0(x0,y0,r0)。

双三次插值法利用了目标插值点周围4个方向上共16个像素点进行插值，如图2所示。不仅要考虑到周围4个直接相邻像素点灰度值对插值点的影响，还需要考虑各个方向上相邻点之间的灰度值变化率[5]。双三次插值算法的一般公式为：

(5)

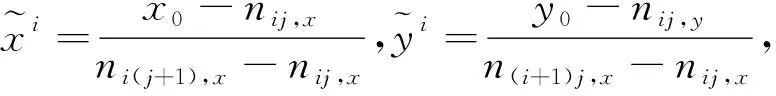
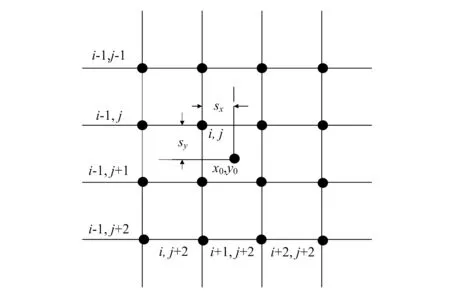
图2 双三次插值

3 基于双三次插值法初始位姿优化

3.1 双三次插值算法理论推导

在2中提到的双三次插值法的基础上，考虑巡检机器人的朝向r，得到新的插值公式：

h(P0,m)=T(rt)Ah(x,m)

(6)

式中：T(rt)为基于机器人转向角度rt的地图坐标系与机器人坐标系之间的旋转变换矩阵;A=[m11m12…mij…m44]，为系数矩阵，其中mij是与图2中16个像素点对应的具有地图特征的激光点云数据，ij即为图2中像素点的位置。式(5)中多项式系数aij的计算依赖于插值数据的特性[8]，常用的方法是用4个顶点的高度以及每个顶点的3个导数来确定，如式(7)～(9)所示。

(7)

(8)

(9)

(10)

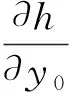
(11)

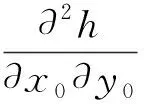
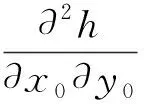
(12)

根据变电站地图实际信息结合初始位姿估计点进行矩阵计算[10]，即可得到插值结果P0(x0,y0,r0)的概率值，从而确定最优初始位姿P0(x0,y0,r0)。

3.2 CERES非线性优化

本文使用CERES非线性优化库来辅助双三次插值算法确定最优初始位姿[12]。通过双三次插值可以得到Ps(x0,y0,r0)的概率值，如果要使得该概率值在栅格地图中最大，那么就需要使得CERES构建得到的优化目标函数值(残差residual)最小，即：

(13)

CERES库辅助求解可以得到置信度、位移、旋转3个残差最小的初始位姿估计点。假定

(14)

式中：Rα为置信度残差；Rtrans为位移残差；Rrot为旋转残差。式(15)为在式(14)的基础上加入了权重。

(15)

权重表示不同参数对结果的不同影响，本文中置信度权重为10/有效激光点数目的平方根，范围为0.3～0.5，位移权重为10，旋转权重为10。

采用CERES优化库对初始位姿进行局部优化匹配，局部匹配是调用real time scan matching来实现的，需要构建OccupiedSpaceCostFunctor这个代价函数的计算模型。

4 实验结果

4.1 实验平台

实验采用亿嘉和科技股份有限公司研制的变电站智能巡检机器人E100，如图3所示。E100面向电力、市政、通信和石化等行业，为智能运维系统提供环境和工业设备状态的监测数据。

图3 E100变电站智能巡检机器人

实现变电站巡检机器人初始位姿优化的具体程序流程如图4所示。

图4 程序总体框图

4.2 实验结果分析

为了证明本文所提方法的优越性，在某变电站实际环境下进行多次实验，并与基于里程计和双线性插值算法的初始位姿估计进行实验对比，使用位置估计误差来进行数据分析，即位姿参考点和相应估计点之间的欧氏距离。具体实验数据见表1。

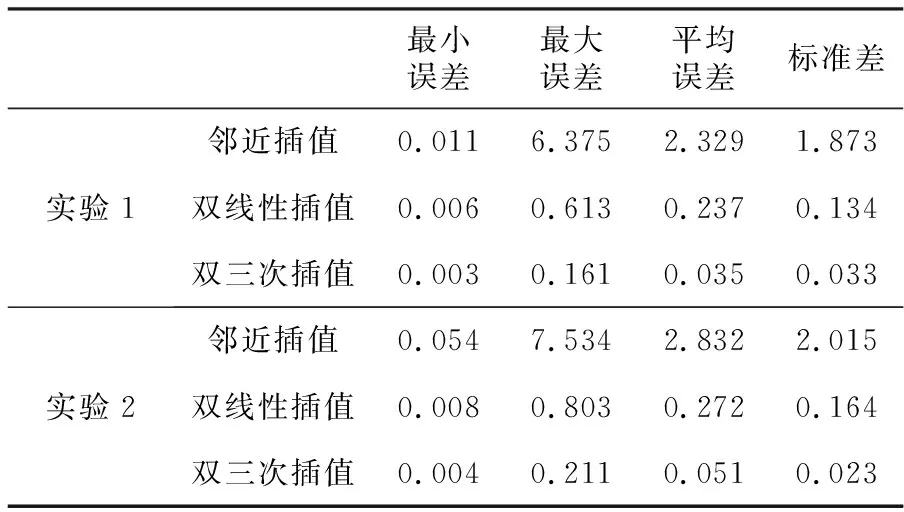
表1 初始位姿估计误差 m

从表中可以看出，实验1中，基于双三次插值的初始位姿估计的最小误差明显小于临近插值算法；与双线性插值算法相比，虽然最小误差相差不大，但是最大误差明显较小；整体的误差平均值以及标准差远小于其他两种方法。

对于实验2，考虑了变电站的实际情况，增加了稀疏环境下的影响因素，增加了障碍物，改变了预计估值点相应的置信度，所以3种方法整体的误差都有所提升，但是双三次插值的位姿估计误差提升较小。

根据实验可以看出，基于双三次插值算法具有较好的初始位姿估计精度，能够抵抗环境干扰，具有较高的鲁棒性。

5 结束语

高精度初始位姿的确定，是变电站智能巡检机器人开发中的关键技术。针对目前初始位姿确定算法鲁棒性差，计算量大，无法适应已知环境中临时出现的轻微变化等问题，本文提出了基于双三次插值算法的巡检机器人初始位姿优化，把局部匹配也是看成了一个非线性优化问题，主要采用双三次插值算法优化初始位姿估值点，实现了变电站环境内智能巡检机器人高精度的初始定位，鲁棒性好，降低了机器人迷路的发生频次，提高了设备巡检的效率和检测数据的可靠性。目前已经在多个变电站实际使用，初始位姿的高度准确性降低了机器人迷路的发生频次，提高了设备巡检的效率和检测数据的可靠性。

参考文献：

[1] 赵珏. 基于激光传感器室内机器人自主导航技术研究[D]. 天津：天津理工大学,2017.

[2] TODD Lupton, SALAH Sukkarieh. Visual-Inertial-Aided navigation for high-dynamic motion in built environments without initial conditions[J]. IEEE Trasactions on Robotics, 2012, 28(1):61-76.

[3] 项志宇. 基于激光雷达的移动机器人障碍检测和自定位[D]. 杭州：浙江大学,2002.

[4] 王璐. 未知环境中移动机器人视觉环境建模与定位研究[D]. 杭州：浙江大学,2007.

[5] 胡良梅，王竹萌，高隽，等. 可信度双三次插值的PMD距离信息和RGB图像数据融合[J]. 中国图象图形学报, 2013, 18(6)：621-627.

[6] 韩轾. 基于ROS的室内移动服务机器人定位与导航系统的研究与开发[D]. 成都：电子科技大学,2017.

[7] 钱堃. 与人共存环境下服务机器人定位导航技术研究及应用[D]. 南京：东南大学,2018.

[8] 陈红丽，曹义亲. 边缘定向的双立方插值算法的研究与应用[J] . 计算机仿真, 2015, 32(4)：180-183.

[9] 李纯龙，潘海侠，王华峰. 自适应立方卷积图像插值算法[J]. 北京航空航天大学学报, 2014, 40(10):180-183.

[10] ZHOU Jing, CHEN Xiaolin, LI Shijun. Centroid localization algorithm based on bicubic interpolation gray square weighted[J] . Engineering Solution for Manufacturing Process, 2013, 655-657：895-899.

[11] LEE Seung-Mok, JUNG Jongdae. Geomagnetic field-based localization with bicubic interpolation for mobile robots[J]. International Journal of Control,Automation, and Systems, 2015, 13(4)：1-11.

[12] 杨大伟，宋程程. 视觉显著运动目标初始定位方法[J] . 计算机工程与应用, 2015, 51(16)：189-191.