切削加工机器人的误差补偿研究
2018-06-01张永贵黄中秋
张永贵,黄中秋
(兰州理工大学机电工程学院,甘肃 兰州 730050)
6R工业机器人是指6个关节均为旋转关节的工业机器人。6自由度关节机器人在切削加工过程中系统刚度远远低于CNC系统的刚度[1]。机器人刚度是描述机器人在外作用力下抵抗变形的能力[2]。当机器人操作臂末端受到外力作用时会产生变形,从而造成切削加工中的误差,而变形量与机器人的刚度和作用力的大小有关[3-4]。机器人的刚度包括伺服刚度和机械刚度,本文只讨论由机械刚度引起的机器人操作末端的变形[5-6]问题。通过叠加机器人关节刚度和臂杆刚度在机器人操作臂末端引起的变形,建立对机器人关节角的补偿模型,并通过对机器人关节角的补偿,减少因机器人刚度问题所造成的机器人在切削加工中的误差[7]。
1 机器人运动学模型
参照文献[8]对MOTOMAN UP50机器人的研究结果,根据机器人的结构参数,运用D-H法建立机器人各连杆的附体坐标系,如图1所示。各连杆的参数见表1。

表1 机器人运动学D-H参数值
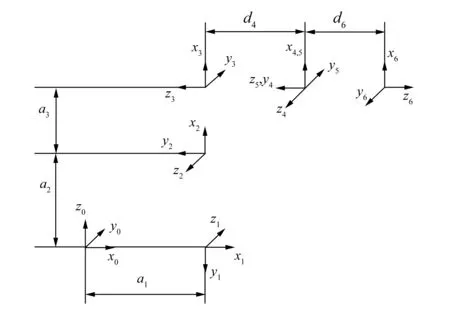
图1 机器人D-H坐标系
定义机器人不同位姿时,坐标系{i+1}与坐标系{i}的变换矩阵为:
Rot(xi+1,αi+1)Trans(xi+1,ai+1)
(1)
式中:oi为机器人第i个关节转角;θi,di,αi,ai分别为机器人零位时的参数值。
(2)
2 不同坐标系间静力的变换
设有一个作用在某个物体上的力F,它使物体发生假想的微分位移D,做出虚功δW。虚拟位移的极限趋向无穷小,所以系统的能量不变。力F所做的虚功为:
δW=FTD
(3)
式中:D为虚拟位移的微分运动矢量;F为力矢量,表示作用在该点的力和力矩。
用坐标系{c}来描述此物体上某个不同的点,有:
δW=FTD=cFTcD
(4)
根据文献[8]第三章式(3.97)有:
cD=JD
(5)
从而有
FT=cFTJ
(6)
对式(6)稍加变换即可得:
cF=[JT]-1F
(7)
式中:J为雅可比矩阵。
式(7)即为各坐标系之间静力的变换公式。
3 机器人刚度模型建立
3.1 机器人关节挠度在操作臂末端的映射
借用文献[9]的方法可以得到机器人关节变形在机器人臂杆末端的挠度映射,即:
(8)
式中:kθ为关节刚度。
针对MOTOMAN UP50机器人,引用文献[9]的公式求得其关节刚度kθ=diag(8.86×109,5.50×109,1.85×1010,3.30×108,2.10×109,8.81×109)N·mm/rad。在此,首先分析机器人在位姿q=[30 60 30 45 30 60]、末端载荷F=[100 150 50 0 0 0]时的末端变形,然后求得在只考虑关节变形时操作臂末端的挠度Δδθ(保留4位小数):
Δδθ=[-0.017 9 0.029 4 0.033 2 0.000 0 0.000 0 0.000 0]
(9)
3.2 机器人臂杆挠度在操作臂末端的映射
通过计算可得到机器人在操作臂末端受到F=[100 150 50 0 0 0]N的力时,臂杆1,2,3,4及臂杆6的挠度变形,见表2~表6。表中的γ为绕z轴的转角,β为绕y轴的转角,φ为绕x轴的转角,Δl为在x轴方向的位移。

表2 臂杆1的挠度变形

表3 臂杆2的挠度变形

表4 臂杆3的挠度变形

表5 臂杆4的挠度变形

表6 臂杆6的挠度变形
因为臂杆5的刚度可以视为无限大,所以臂杆5在结构中没有挠度变形。根据各个臂杆的挠度变形可得臂杆变形在操作空间所产生的广义挠度Δδl为:
Δδl=[ 0.042 5 0.020 4 -0.012 4 0.000 0 0.000 0 0.000 0]
(10)
3.3 机器人操作臂末端刚度
通过叠加操作末端的关节挠度和臂杆挠度从而得到机器人的总挠度,即:
Δδ=Δδθ+Δδ1
(11)
已知机器人操作臂末端的广义力F和总挠度Δδ,则机器人总的空间刚度K为:
(12)
4 切削加工机器人操作臂末端位移误差的计算
4.1 操作臂末端铣削力的计算
根据材料力学可知铣削力F的计算公式为:
(13)
式中:CFz为铣削力的切削系数;d0为铣刀直径;ae为铣削深度;af为每齿进刀量;ap为铣削宽度;z为铣刀齿数;kFz为修正系数。
根据铣削条件取CFz=160,d0=8mm,ae=8mm,ap=5mm,af=0.2mm/齿,z=4,kFz=3.54,代入式(13)中可得F=2 551N。
从而可得到各铣削分力分别为:Fx=1 020.4N,Fy=2 040.8N,Fz=2 295.9N。
4.2 操作臂末端误差的计算
将求出的各铣削分力代入式(12)即可计算出机器人末端误差Δx为(保留四位小数):

(14)
5 机器人的关节角补偿模型的建立
雅可比矩阵是一个多元函数的偏导矩阵,假如有一组变量为xj的方程Yi(其中i,j=1,2,…,6)为:
Yi=fi(x1,x2,…,xj)
(15)
由Yi的微分变化所引起的xj的微分变化为:
(16)
同样,根据上述关系,对机器人的位置方程求微分,可以写出以下方程:
Δx=JΔθi
(17)
因此在已知机器人末端误差Δx时,可以根据式(17)来求关节补偿量Δθi,即:
Δθi=J-1Δx
(18)
6 实验验证以及数据分析
6.1 试验验证
为了验证所建立的关节角补偿模型是否有效,从机器人示教器读取机器人不同位姿时的关节位置和操作臂末端姿态。观察点的位姿,如表7所示(由于篇幅限制,只列出8组数据)。
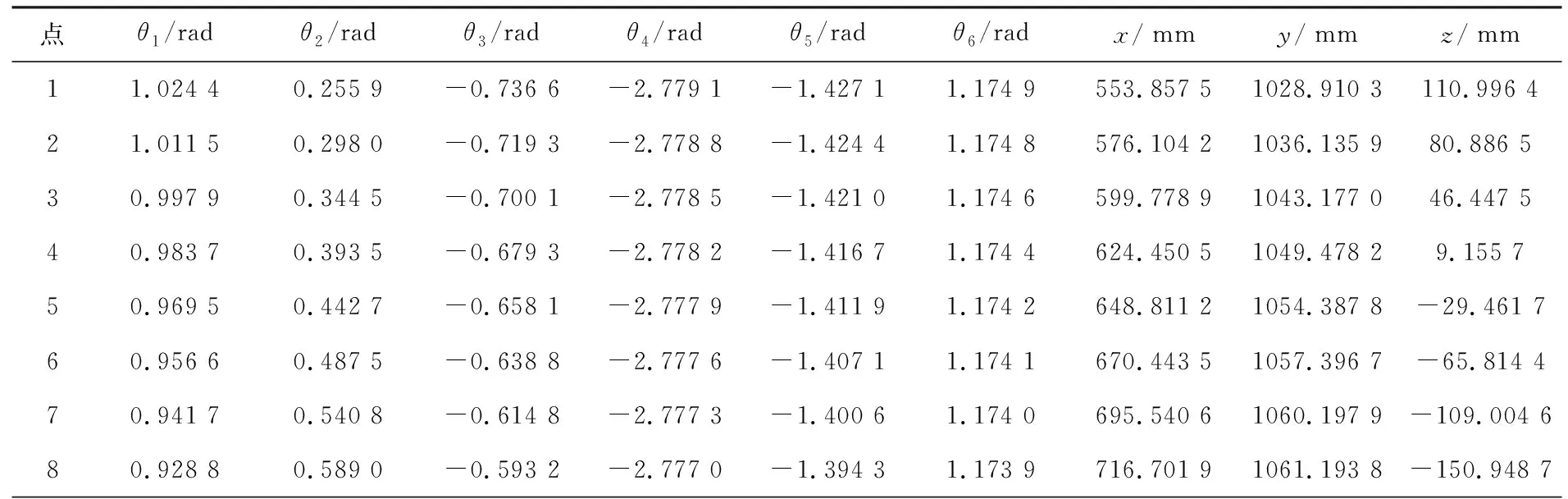
表7 观察点的关节位置和末端位置
根据表7中的关节角θi由式(17)、(18)可计算出各关节角的补偿值Δθi,见表8。
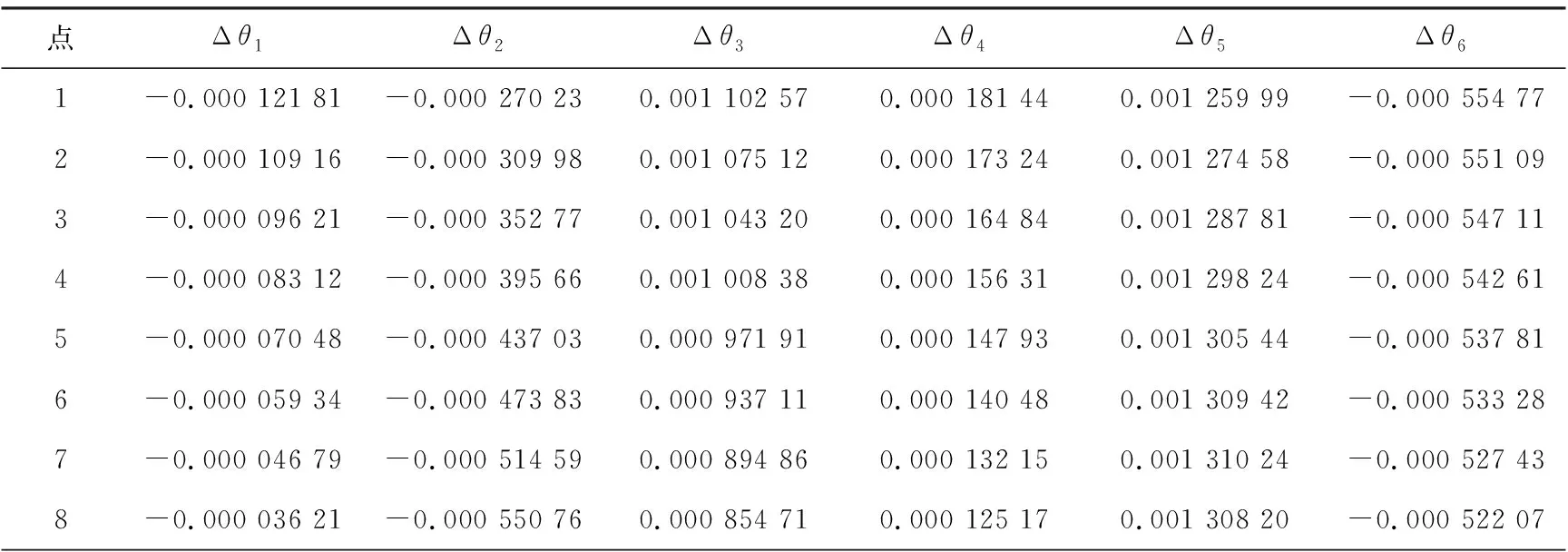
表8 关节角补偿值 rad
对关节角进行补偿后得到的观测点的数据见表9。
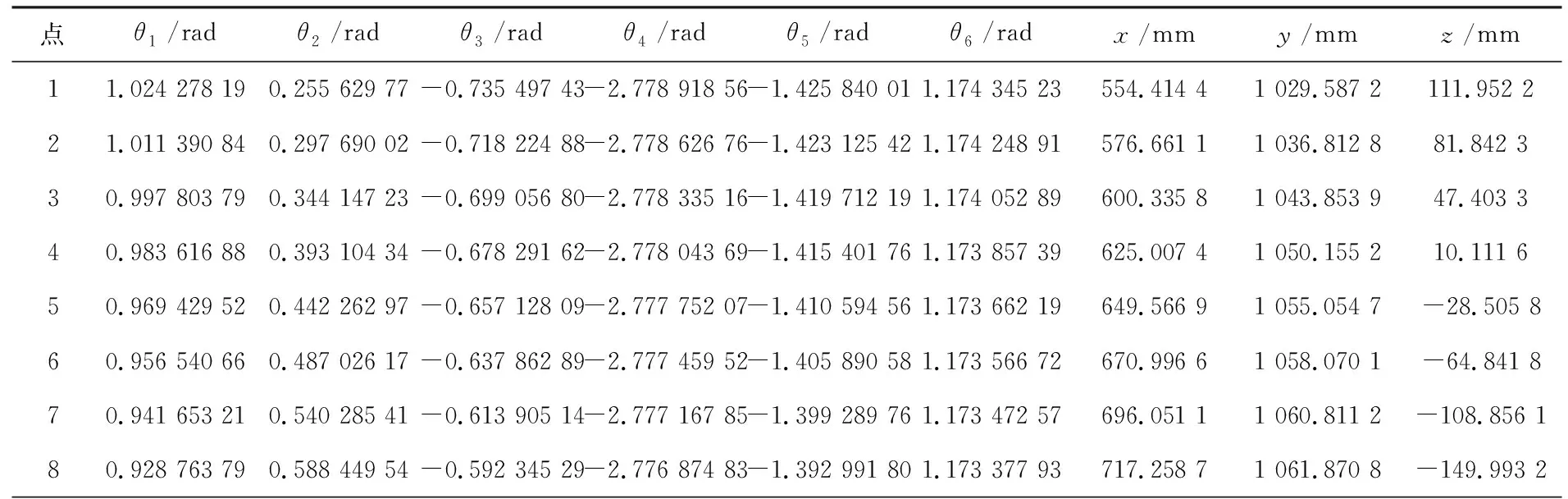
表9 关节角补偿后观察点的关节位置和末端位置
补偿前与补偿后观察点末端位置变化见表10。
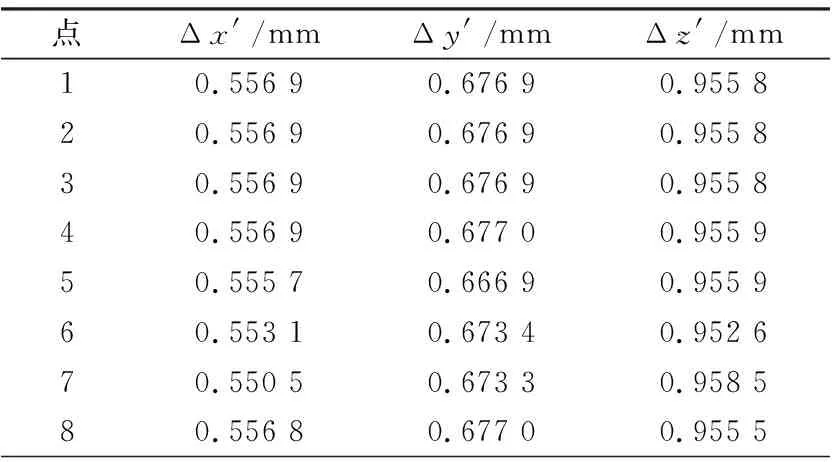
表10 末端位置变化
6.2 数据分析
由式(14)可知,由于机器人自身刚度的原因会造成机器人在切削加工中,其刀具在x,y,z3个方向上分别少走了0.557 1mm、0.677 5mm、0.955 1mm,因此产生了加工误差。为了补偿加工误差,通过对机器人关节角进行补偿来修正。而根据表10可知,补偿关节角后,其刀具在x,y,z3个方向上分别平均多走了0.555 462 5mm、0.674 787 5mm、0.955 725 0mm,从而可得刀具在x,y,z3个方向上的补偿效果分别为99.71%、99.60%、99.93%,由此可知补偿是有效的。
7 结束语
本文对MOTOMAN UP50机器人进行了刚度分析及操作臂末端切削力的分析,建立了机器人的刚度模型和末端切削力模型,并根据其刚度模型和末端切削力模型建立了机器人的误差补偿模型,为误差补偿提供了新的思路。通过关节角补偿实验,验证了该补偿方法的可行性。
参考文献:
[1] 陈玉山.6R 型工业机器人关节刚度辨识与实验研究[D].武汉:华中科技大学,2011.
[2] 尼库,富春.机器人学导论及应用[M].北京:电子工业出版社,2004.
[3] 张永贵,刘晨荣,刘 鹏.工业机器人刚度分析[J].机械设计与制造,2015(2):1-5.
[4] 张玄辉.工业机器人刚度的辨识方法与性能分析[D].武汉:华中科技大学,2009.
[5] JUDD R P,KNASINSKI A B.A technique to calibrate industrial robots with experimental verification[J].Robotics and Automation,IEEE Transactions on,1990,6(1):20-30.
[6] SUNADA W H,DUDOWSKY S.On the dynamic analysis and behavior of industrial robotic manipulators with elastic members[J].Journal of Mechanical Design,1983,105(1):42-51.
[7] 黄心汉.机器人刚度的测试方法[J].机器人,1988(3):45-50.
[8] 熊有伦.机器人技术基础[M].武汉:华中科技大学出版社,1995.
[9] 张永贵,刘文洲,高金刚.6R工业机器人刚度模型及应用研究[J].农业机械学报,2014(2):35-42.
