基于过完备字典稀疏表示振动信号压缩感知方法
2018-06-01郭俊锋
石 斌, 郭俊锋
(兰州理工大学机电工程学院,甘肃 兰州 730050)
在日常生活和工程实践中,存在着大量的机械振动现象。机械振动信号包含着机械设备工作过程中所蕴含的大量的信息,利用这些振动信息人们可以更加深入地了解机械设备工作过程中的内在机理和特征,为更好地开发利用机械设备提供理论和技术支持。传统的且目前被广泛采用的振动信号检测与采样系统为基于奈奎斯特采样定理的采集系统,必然会产生大量的监测数据。
近年来出现的压缩感知采样突破了传统的奈奎斯特采样定理,只要信号是可压缩的或在某个变换域上是稀疏的,就可以基于压缩感知理论对其进行低速观测,然后通过合适的重构算法就可以实现信号的复原,给机械振动信号的采样、存储和处理带来极大的方便。压缩感知理论的一个重要的基础和前提是信号足够稀疏,因此信号的稀疏域的选择就显得尤为重要,只有选择合适的包含振动信号信息的过完备字典才能保证信号的稀疏度,从而保证信号的重构精度。
常用的正交基字典不能完整地包含振动信号的信息,振动信号在该稀疏方式下不够稀疏,造成振动信号压缩重构精度较低。目前,经典字典学习算法构造相关信号的过完备字典被广泛关注,由于这类字典灵活性好、自适应强,较完整地包含了信号的信息和特征,所以在信号压缩、去噪和特征提取等方面被大量采用。经典字典学习算法有MOD算法[1]、K-SVD算法[2]和双稀疏字典算法等[3]。本文提出基于过完备字典稀疏表示机械振动信号压缩感知方法,重点研究适合机械振动信号的字典学习算法,用字典学习算法训练适合机械振动信号的过完备字典,使得振动信号在该过完备字典上有较好的稀疏性,提高振动信号的压缩率和压缩重构精度,并通过选用美国西储大学轴承数据验证基于过完备字典稀疏表示机械振动信号压缩感知方法的有效性。
1 压缩感知
压缩感知[4-6]的前提是Rn空间的信号f可稀疏表示为:
f=Θα
(1)
式中:转换矩阵Θ=[φ1,φ2,…,φn];系数向量α=ΘTf,其中α仅有k(k≪n)个非零系数。对信号f进行压缩感知采样得到观测向量y:
y=Ψf
(2)
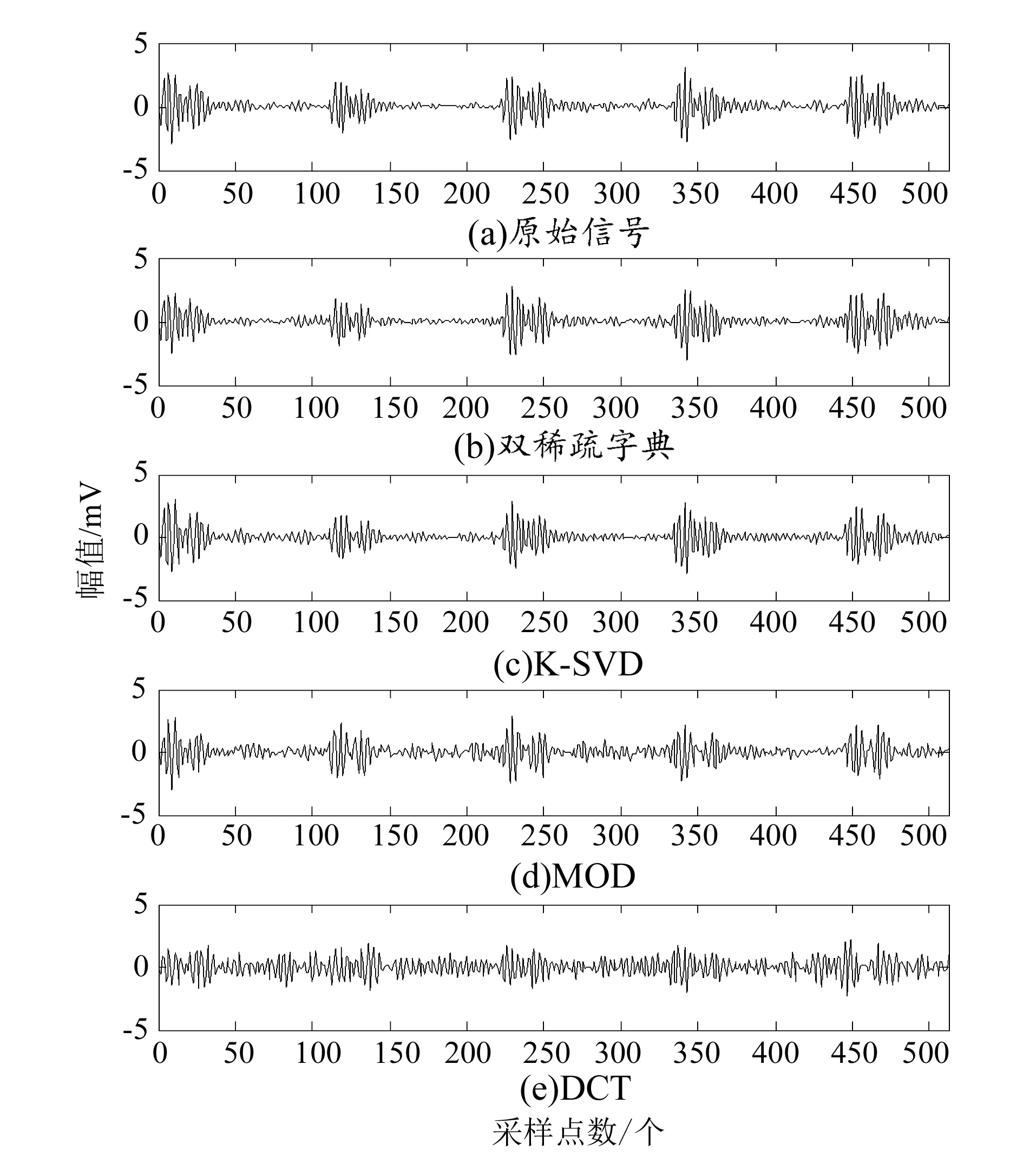
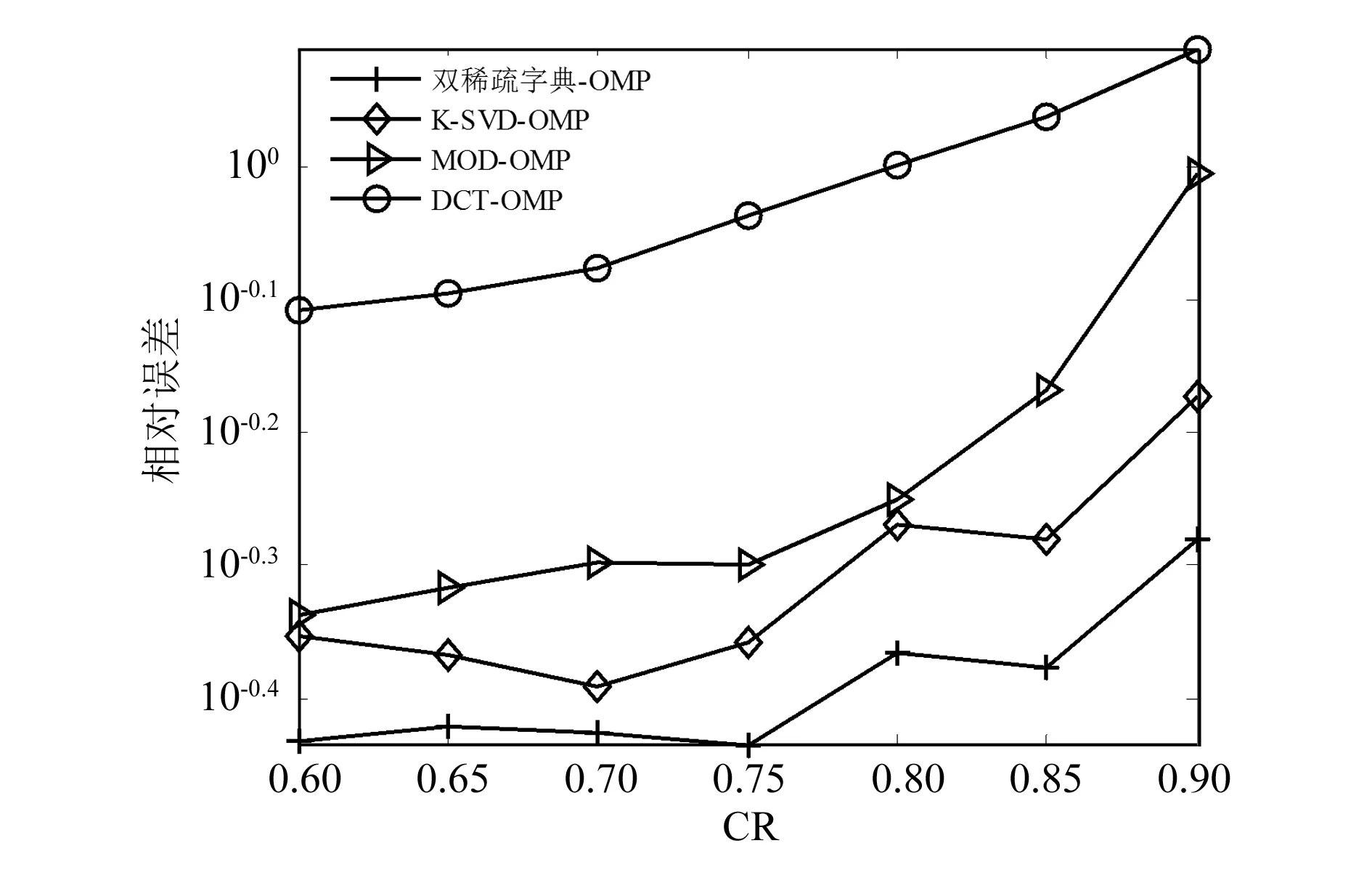
式中:Ψ为一个m×n的测量矩阵,与Θ不相关且m≪n。当α是k稀疏且k min‖α‖0 s.t.y=Ψf=ΨΘα (3) 然而,有些信号在上述正交变换基Θ下仍不稀疏或不够稀疏,因此可以采用适合信号本身特征的过完备字典D对信号进行稀疏表示。按照压缩感知理论[7],测量矩阵一般为高斯随机矩阵,若存在某个变换D∈Rn×K使得f=Dα,则式(3)可写为: min‖α‖0 s.t.y=Ψf=ΨDα (4) 式(3)和式(4)的求解方法是正交匹配追踪算法(OMP)[8],本文采用该算法来进行振动信号的压缩测量与重构。 (5) 式中:αi为A的第i列;T0为非零元的个数。字典D通常是过完备字典。MOD算法首先选取一个初始字典,然后通过初始字典和信号集求解稀疏表示系数矩阵,最后通过得到的稀疏表示系数矩阵求解更新字典。MOD算法描述如下。 1)初始化字典:建立D(0)∈Rn×K。 2)标准化:标准化D(0)的列。 稀疏分解阶段:已知字典D与信号集X,根据式(6)用OMP算法逐列求解稀疏系数矩阵A。 (6) 字典更新阶段: 用式(7)更新字典。 X(A(k))T(A(k)(A(k))T)-1 (7) 4)输出:更新后的字典D。 双稀疏字典基本概念是将现有的过完备字典D的每一个原子在预先定义的基字典Φ上进一步稀疏表示,其模型为: D=ΦA (8) (9) 式中:t,p分别为信号和稀疏字典A原子的非零元素个数;Γi为系数矩阵Γ中第i个字典原子对应的系数列向量;其算法具体步骤如下[9]。 1) 输入:训练样本X,基字典Φ,初始字典表示系数A0,字典原子稀疏性上限p,训练样本稀疏性上限t,迭代次数J。 2) 初始化:A=A0。 3) while(迭代次数 ①稀疏编码:用OMP分解算法求解信号在当前字典下的稀疏表示,其需满足的模型为 其中γ为稀疏向量。 ②字典更新:逐一对A中每列αj进行更新。 forj=1,2,…,K 令I={应用到αj原子表示的样本索引} 对下式进行基于基字典Φ的稀疏表示,即可求出更新后的αj: 令Aj=αj End for End while 4)输出:满足迭代停止条件后,输出A,然后与基字典Φ相乘就得到所需的字典D。 本文采用相对误差来衡量振动信号的重构性能,采用压缩率来衡量振动信号的压缩度,其定义如下。 1)相对误差( relative error)是指振动信号的绝对误差与原始信号之比。其定义为 (10) 2)压缩率CR(compression rate),用其来衡量振动信号的压缩度,CR越大,信号压缩率越高。其定义为 (11) 式中:n为原始振动信号长度;m为压缩测量信号长度。 为有效验证本文所采用的算法,分别比较双稀疏字典学习算法训练所得过完备字典、K-SVD学习算法训练的过完备字典、MOD学习算法训练的过完备字典和固定字典DCT过完备字典4种不同稀疏方式下压缩重构的相对重构误差和重构时间。 采用双稀疏字典算法构造机械振动信号过完备字典时,基字典Φ选取为K-SVD学习算法训练振动信号的过完备字典512×600,稀疏表示系数字典A是随机选取样本信号在基字典上稀疏分解后的系数矩阵600×750,p=5,t=2,J=4,N=1 000。当测量矩阵Ψ为102×512,通过公式(11)得压缩率为80%。在压缩率CR为80%的情况下,选取西储大学轴承数据库中的轴承外圈故障类型,故障直径为0.007英寸、故障点位于6点钟方向(OR007@6)的信号数据进行测试,该数据分别由电机驱动端和风扇端12点钟的位置的加速度传感器采集所得。因该轴承外圈故障数据是周期信号,为了训练字典所要求的大数据量的需要,故将信号从0~121 991采样点扩展到0~731 946采样点。驱动端和风扇端数据的过完备字典生成训练都用0~716 800采样点,压缩感知测试信号用730 000~731 946采样点。图1和图2分别为驱动端信号和风扇端信号在不同过完备字典稀疏方式下的重构效果图。从图1和图2可以看出,基于双稀疏字典学习算法所得过完备字典的重构振动信号比其他3种稀疏方式下的重构信号更接近原始振动信号。不同振动信号和稀疏方式下的重构误差和时间见表1,由于DCT过完备字典稀疏方式下的重构误差太大,未能重构原始信号,重构精度较差,因此只给出双稀疏字典学习算法训练所得过完备字典、K-SVD过完备字典和MOD过完备字典3种稀疏方式下的重构误差和时间。从表中可以看出,基于双稀疏字典学习算法训练振动信号所得过完备字典稀疏方式下在驱动端和风扇端重构误差为0.308 1和0.706 1,比其他稀疏方式下的重构误差都小,MOD稀疏方式下重构时间相对较少,但是其重构误差大,重构精度较差,在保证较高重构精度和较短重构时间的前提下,振动信号在双稀疏字典稀疏方式下比在K-SVD稀疏方式下的重构误差小,重构精度更高,重构时间更短。 图1 驱动端振动信号在不同稀疏方式下的重构 图2 风扇端振动信号在不同稀疏方式下的重构 双稀疏算法的参数设置与固定压缩率下的参数设置相同,实验时每个压缩率下运行5次重构误差求平均值,如图3和图4所示。 图3 驱动端振动信号在不同压缩率和稀疏方式下的重构 图3为驱动端信号在压缩率为60%~90%时4种稀疏方式下的压缩重构的相对误差曲线,不同压缩率下,基于双稀疏字典学习算法构造过完备字典稀疏方式下相对重构误差均小于其他3种稀疏方式下的重构误差。驱动端信号在4种稀疏方式下的压缩重构误差和时间见表2,基于DCT过完备字典和MOD过完备字典两种稀疏方式下信号压缩重构时间较短,但是重构误差较大,振动信号失真度较大,在保证有较高的重构精度的前提下,双稀疏字典稀疏方式下的重构误差比K-SVD稀疏方式下的重构误差小,重构时间也相对较少。 图4 风扇端振动信号在不同压缩率和稀疏方式下的重构 表2 驱动端信号的重构误差和时间 图4为风扇端信号在压缩率为60%~90%时,基于双稀疏字典学习算法构造过完备字典稀疏方式下和其他3种稀疏方式下的压缩重构的相对误差曲线,图3与图4具有相同的效果。风扇端信号在4种稀疏方式下的压缩重构误差和时间见表3,表3与表2具有相同的效果。 表3 风扇端信号的重构误差和时间 针对常用的正交基字典不能够灵活地表示振动信号的复杂性,振动信号在该稀疏方式下不能足够稀疏,影响振动信号压缩重构精度,本文提出了基于过完备字典稀疏表示机械振动信号压缩感知方法,该算法基于经典字典学习算法构建过完备字典,准确稀疏表示机械振动信号,提高振动信号压缩感知重构性能。当CR在60%~90%时,基于双稀疏字典算法构造的过完备字典压缩重构相对误差比基于MOD算法和K-SVD算法都小。 参考文献: [1] ENGAN K,AASE S O,HUSOY JH. Method of optimal directions for frame design[C]//Proceedings of the 1999 IEEE International Conference on Acoustics,Speech,and Signal Processing.Phoenix:AZ,1999:2443-2446. [2] AHARON M,ElAD M,BRUCKSTEIN A. K-SVD:an algorithm for designing overcomplete dictionaries for sparse representation[J].IEEE Transactions on Signal Processing,2006,54(11):4311-4322. [3] RUBINSTEIN R,ZIBULEVSKY M,ELAD M. Double sparsity:learning sparse dictionaries for sparse signal approximation[J].IEEE Transactions on Signal Processing,2010,58(3):1553-1564. [4] CANDES E,ROMBERG J,TAO T. Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory,2006,52(2):489-509. [5] CANDES E,WAKIN M. An Introduction to compressive sampling[J].IEEE Signal Processing Magazine,2008,25(2):21-30. [6] DONOHO D. Compressed sensing[J].IEEE Transaction on Information Theory,2006,52(4):1289-1306. [7] CANDES E,ELDARB Y C,NEEDELL D,et al. Compressed sensing with coherent and redundant dictionaries[J]. Appliedand Computational Harmonic Analysis,2011,31(1):59-73. [8] TROPP J A,GILBERT A C.Signal recovery from random measurements via Orthogonal Matching Pursuit[J].IEEE Transactions on Information Theory,2007,53 (12):4655-4666. [9] 银壮辰. 基于稀疏表示和字典学习的图像去噪研究[D]. 武汉:武汉理工大学,2014.2 基于经典字典学习算法的机械振动信号的过完备字典设计
2.1 MOD算法
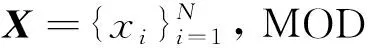
2.2 K-SVD算法
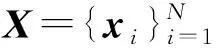
2.3 双稀疏字典算法


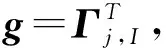
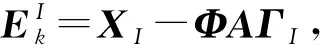
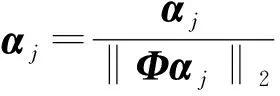

3 实验与分析
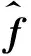
3.1 固定压缩率下的振动信号重构误差和时间比较

3.2 不同压缩率振动信号重构误差和时间比较

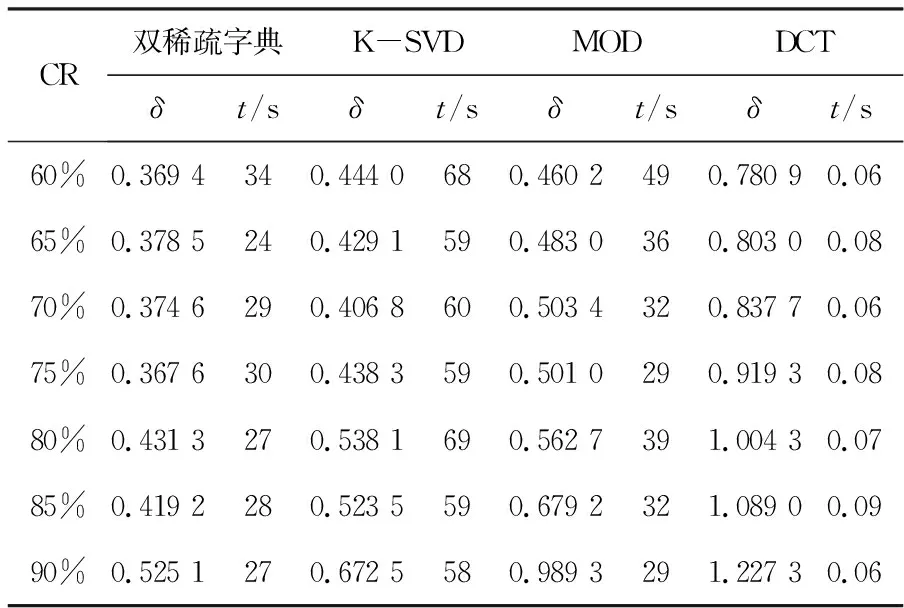
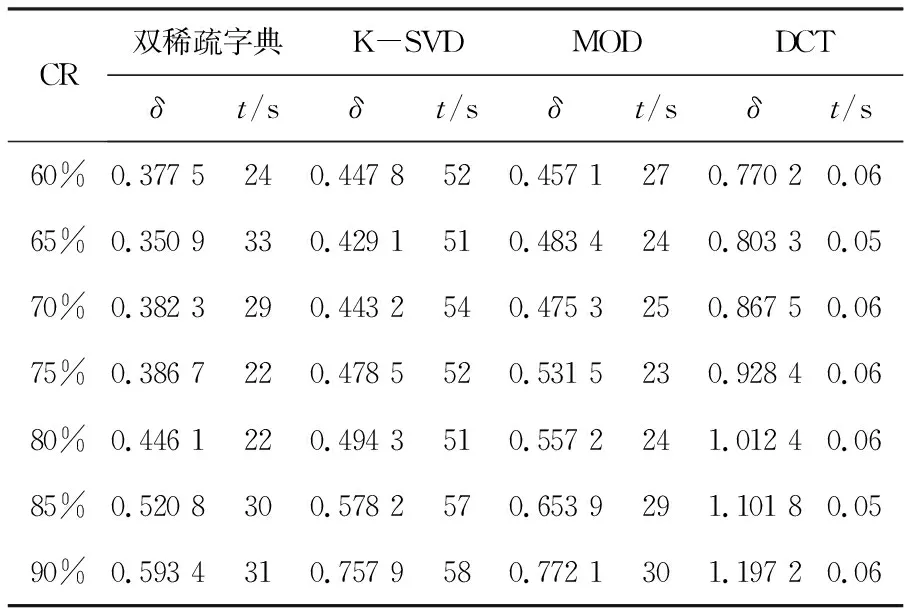
4 结束语
