基于神经PID带位置补偿器的AGV旋转平台随动控制

，，， ，

(1.南京航空航天大学机电学院，江苏 南京 210016；2.江苏省精密与微细制造技术重点实验室，江苏 南京 210016)

0 引言

随着近几年电商的急速发展，传统的物流仓储行业面临了极大的挑战，如何提高存储效率、提高存储密度、实现对数量巨大、品类繁多商品的搬运和分拣同时降低劳动强度和分拣的出错率成为各大电商普遍面临的问题[1-2]，自动导引[3-5]AGV(automatic guided vehicle)成为各大物流仓储行业寻求突破口的关键。提高AGV的灵活性，实现AGV旋转平台的位姿调节和控制在电商用AGV中越来越重要。因此，实现AGV旋转平台随动控制的动态性能和随动控制的精度是至关重要的。

参考文献[6]提出了一种随动控制方法用于高精度的随动控制，该方法首先对被跟踪的对象即主动系统进行分类，采用改进最小二乘法和多项式拟合相结合的方法实现高精度的随动控制。参考文献[7]针对大功率随动实验台中多台电机的同步控制提出了一种同步控制策略，并将滑模变结构控制引入到控制算法中，为了抑制系统的高频抖动，该文引用开关切换函数，但该方法只能起到一定的一种作用，而无法从根本上避免此类问题。参考文献[6]和参考文献[8]均实现了较高的位置跟踪，但在有严格的速度或角速度要求的随动系统中同时跟踪过程中的误差积累有一定要求，即希望随动系统对速度和角速度有较高的跟踪精度和响应时间，同时希望系统在运行的过程中系统的位置或角度误差控制在一定范围内，对于这样的系统参考文献[6]和[8]显然就显得有所欠缺了。针对此类问题，同时避免文高频抖动问题，提出了一种带位置补偿器的BP神经网络PID控制。

1 AGV旋转平台模型建立

AGV旋转平台的随动控制是指当AGV进行路径跟踪运动时，以AGV车体的旋转角速度为输入，对车上的旋转平台的控制，从而实现对旋转平台搬运的货物位姿的调节。因此如何保证AGV在运行的过程中保持AGV的旋转平台按预定速度稳定运行，并且在AGV搬运货物过程的连续运行过程中，保证系统的角度响应延迟或系统波动造成的误差累积是要解决的问题，首先建立系统的输入输出模型。

采用两轮差速驱动的AGV[9]。差速驱动的AGV通过左轮的速度vl和右轮的速度vr差实现AGV的转向的，在转向的过程中AGV的底盘也在做平面运动，现分析AGV旋转平台的转动。

如图1所示为AGV旋转平台运动学的模型，建立AGV在笛卡尔坐标系中的运动学方程。图中∑XOY为笛卡尔坐标系，AB为AGV底盘的宽度，即两驱动轮的间距D。图中的旋转平台和底盘之间有相对旋转运动。设某一瞬时AGV的运动状态如图1所示,此瞬时AGV绕瞬心C作瞬时转动，C为此刻的瞬心，AC为此时AGV绕瞬心C转动的转动半径，由理论力学的知识可知，此时AGV作平面运动，在笛卡尔坐标系中的角度度为ω，即绝对角速度为：

(1)

若在AGV在运行过程中，需确保AGV上的旋转平台的绝对位姿保持不变，即旋转平台的绝对角速度ωp=0，则在运行过程中即可保证AGV在运行中所搬运货架的位姿的绝对朝向保持不变。在如图1所建立的笛卡尔坐标系中，规定角速度的方向为顺时针时为正，反之，当角速度方向为逆时针时为负。设在图示的瞬时旋转平台控制器的角速度输出为ωo，则有：

ωp=ω﹢ωo

(2)

式(2)即为AGV运行过程中，旋转平台的运动学方程，其中ωo为和控制旋转平台的电机或控制器的角速度输出。

当ωp=0时，即为了保证无论AGV如何运动时旋转平台的绝对朝向不变，此时可得控制量为：

ωo=-ω

(3)

式(3)即为保持下文随动控制系统的运动学方程，显然该方程是一个简单的线性方程，并且该运动学方程是在理想模型的基础上建立的，为未考虑系统扰动的理想模型。

2 带位置补偿器的的AGV旋转平台随动控制

2.1 AGV旋转平台的PID随动控制方法

在自动化控制工程中，PID控制是经典控制也是一种被工程中广泛采用的一种控制方法[10]。通过前面的建模，可得旋转平台的PID控制规律的数学表达式为：

(4)

uo为控制量，KP，τI，TD为常数。

在一般的嵌入式控制器中，均是通过分步实现过程控制的，即实际的控制系统是离散的，而上述讨论的是连续的时间系统，故将式(4)离化并结合本章的旋转平台的控制模型可得：设AGV旋转平台的角速度的控制量为ωc，偏差为ωe，随动过程中的目标角度度为ωo，则

Td(ωe(kT)-ωe((k-1)T)))

(5)

为表述方便，将式(5)中的ωc(kT)，ωe(kT)分别以ωc(k)，ωe(k)代替，有：

Td(ωe(k)-ωe((k-1)))

(6)

ωe(k) =ωo(k)-ωa(k)表示AGV旋转平台的角速度误差，ωa(k)为实际采集到的旋转平台的角速度。由式(6)不难得到下式：

Td(ωe(k-1)-ωe(k-2)))

(7)

式(6)和式(7)相减可得：

Td(ωe(k)-2ωe(k-1)+ωe(k-2))

(8)

式(8)即为离散系统的PID控制。其控制算法程序框图如图2所示。

2.2 AGV旋转平台的神经PID控制方法

神经网络控制起始于上世纪80年代，由人工神经网络和控制理论相结合而发展起来的控制理论，是智能控制的一支[11]。常规的PID控制的局限性在于PID参数的整定往往难以达到最优状态，特别是当系统的运动状态发生改变时，PID无法实时调节参数从而适应变化的系统，控制效果会随之变差，严重会造成系统失稳。而神经网络是一种可以通过系统实际性能合理分配三者之间的比重和关系，对旋转平台的随动PID控制器的各个参数进行实时的在线分配，以达到最佳的控制效果。神经PID控制可以弥补传统PID控制参数不能在线整定的缺点。

如图3所示，AGV旋转平台的随动控制系统采用PID和神经网络，在角速度随动控制过程中，角速度的偏差值通过状态变换器结合权值得到AGV旋转平台的角速度控制量，而权值又根据偏差的状态通过学习算法实时调整，该控制器增强了AGV旋转平台随动控制的角速度的动态响应性能，通过HEBB学习规则使PID参数能够根据系统的运行状态实时调节达到最优，同时采用神经PID也增强了系统的适应能力。可得学习及控制算法如下：

(9)

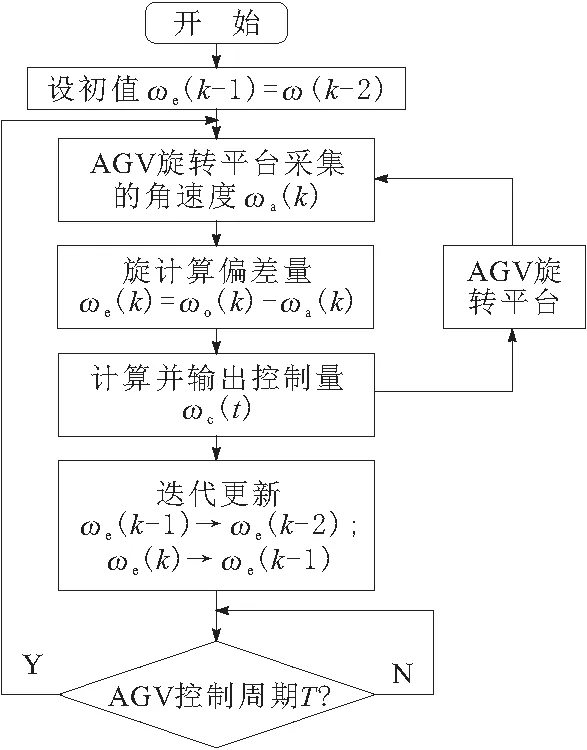
图 2 AGV旋转平台的离散PID控制流程

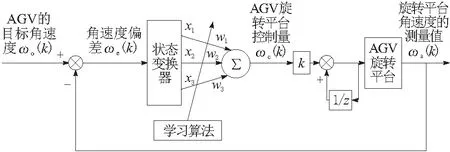
图3 单神经元的AGV旋转平台的随动PID控制系统结构

式中，wi为神经控制的权值，μI，μP，μD分别为比例、积分、微分的学习速率；μk为神经元的比例系数。需要指出的是提高AGV旋转平台对角速度随动控制的响应时间可以增大μk但系统超调也会随着增大，严重可能会造成系统失稳；若控制系统的控制周期较大，系统存在较大的时滞，为使其运行稳定应取较小的μk[12]。

PID参数的在线学习修正主要与AGV旋转平台的角速度的偏差ωe(k)和Δωe(k)有关[12]，因此将AGV旋转平台的随动神经PID控制中的加权系数学习修正即式(9)中的xi(k)用ωe(k)﹢Δωe(k)代替，则上述各式可改写为：

(10)

Δωe(k)=ωe(k)-ωe(k-1);z(k) =ωe(k)；μk为神经元的比例系数，且μk﹥0。式(10)修改后的算法，其参数可根据经验来确定，如此，在AGV旋转平台的随动控制中就兼顾了神经和PID控制的特点。

2.3 带位置补偿的AGV旋转平台的神经PID随动控制方法

上述的神经PID控制算法能够保持对旋转平台输入角速度的随动跟踪，但是在跟踪的过程中，由于跟踪的时滞性和系统的干扰等因素总会在角速度跟踪的过程中有角度误差的积累，这种误差的积累具有随机性，并且会随着运行过程中逐渐积累，并且长时间运行会造成大的角度偏差的积累，即运行一段时间旋转平台或其所搬运的货物的朝向会有大偏差。

图4 带位置补偿器的AGV旋转平台神经PID随动控制系统结构

为了解决上述旋转平台角速度跟踪过程中的角度误差积累的问题，对前述的AGV旋转平台角速度的神经PID随动控制加入位置补偿器，其系统框图如图4所示，在AGV旋转平台随动控制的输入ωo(k)之前加入位置补偿器，该位置补偿器的为双输入单输出。位置补偿器输入为[ωro(k), Δθ(k)]，输出仍为ωo(k)，该输出即为神经PID AGV旋转平台随动控制系统的输入，如前所述。其输入中的ωro(k)为AGV旋转平台角速度的目标值。位置补偿器的基本原理是，当AGV旋转平台的角度误差积累到一个给定的阈值Δδ时，位置补偿器开始工作，当通过减小或增大输出值达到调节的作用，如下式所示：

(11)

式中ωo(k)为AGV旋转平台的目标角速度经过位置补偿器调节后的输出；ωro(k)为AGV旋转平台角速度补偿器的输入即旋转平台的目标角速度，Δδ为AGV补偿器的阈值，Δθ为AGV旋转平台的实际朝向和目标朝向之间的角度偏差，Δω为AGV旋转平台角速度的调节系数，Δω越大，则当角度偏差Δθ超过阈值时调节的时间越短，反之，消除误差的时间越长。因此要合理选择Δω。

3 数字仿真与实验

为验证本章提出的基于BP神经带位置补偿器的的AGV旋转平台随动PID控制算法的可行性和效果，本节对上文提出的算法进行数字仿真和实验。

首先针对AGV旋平台的随动PID控制和AGV旋转平台的随动神经PID控制对角速度跟踪的效果进行仿真对比。跟踪的角速度取正弦信r=0.50sin 2πFt，F=1.0 Hz。取AGV角度补偿器的阈值Δδ=10°，AGV旋转平台角速度调节系数Δω=0.05 rad/s。仿真效果图如图5和图6所示。

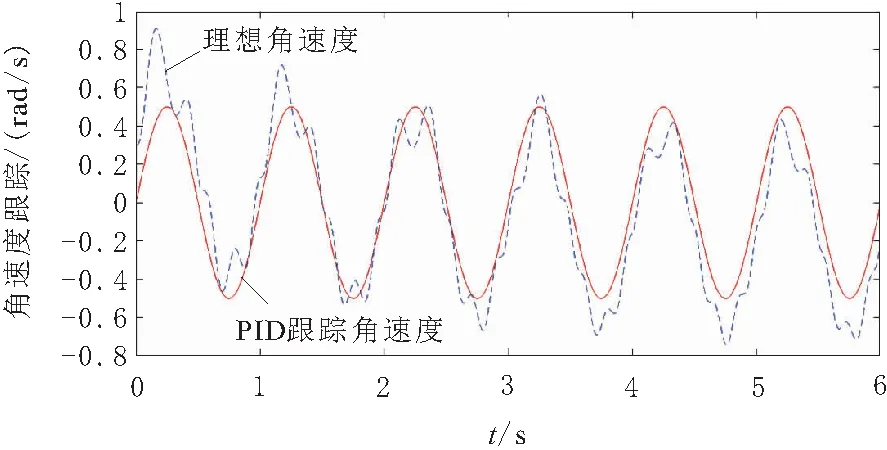
图5 AGV旋转平台的随动PID正弦角速度跟踪仿真

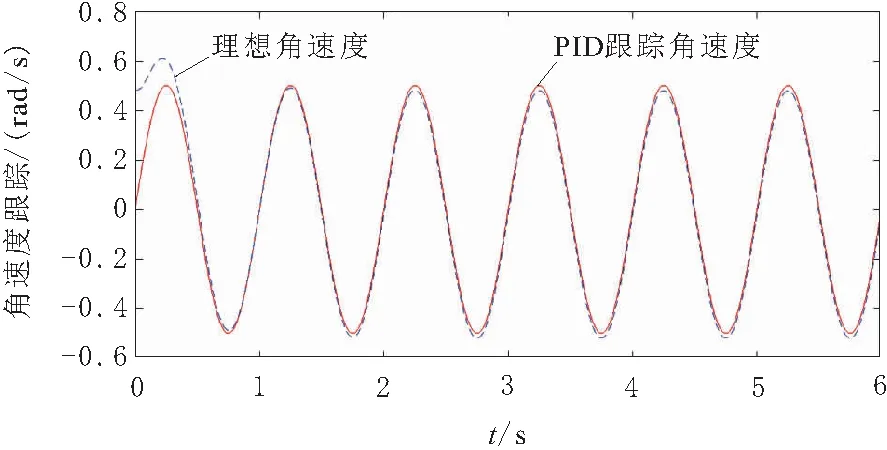
图6 AGV旋转平台的随动神经PID正弦角速度跟踪仿真

对比图5和图6可知，无论是AGV旋转平台的随动PID控制还是神经PID控制均能实现对旋转平台的正弦变化的角速度实现稳定的跟踪 ，即对正弦变化的角速度的随动控制，两者均没有出现发散失稳的现象，两者均是可行的。但从仿真的效果看，显然AGV旋转平台的随动神经PID控制更能实现平滑的跟踪，且跟踪的效果更好即神经PID对于正弦角速度曲线的拟合的偏差更小，对正弦曲线的波动较小。而PID控制对于变化的角速度的跟踪效果更差，在跟踪曲线上的则表现为围绕着跟踪的正弦曲线有较大的角速度波动，特别是当被跟踪的角速度有较大变化值这种波动更大。

如图7所示，AGV的路径跟踪轨迹如图中所示，在路径跟踪的过程中，旋转平台为随动控制，底盘的路径跟踪过程中底盘的旋转角速度为旋转平台的控制输入，旋转平台控制的目的是但底盘产生旋转角速度时，迅速产生控制量，使旋转平台的绝对朝向不变，同时当旋转平台的角度误差积累一定值时消除角度误差。

图7 AGV旋转平台随动跟踪实验

图8为AGV在进行路径跟踪过程中，当AGV底盘产生角速度时其旋转平台角速度的随动控制，采用第2章的控制算法。由图可知，在角速度的跟踪过程中，系统的响应快，且角速度跟踪的精度也比较高。

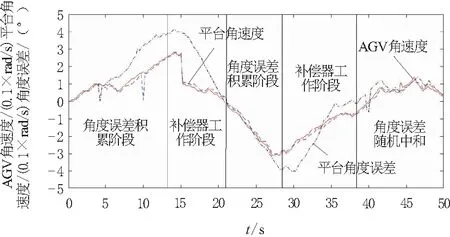
图8 AGV旋转平台角速度随动控制

在图8的旋转平台的随动控制中，其控制过程中加入了位置补偿器。在AGV刚开始运行时，由于旋转平台响应存在的迟滞，会造成系统的角度偏差存在积累，如图所示，在0～13 s的运行阶段为旋转平台的角度误差不断积累阶段，当角度误差达到阈值Δδ=4°时，位置补偿器开始主动调节旋转平台的角速度，从而使角度误差向0收敛，图中13～21 s内为位置补偿器工作阶段，该阶段旋转平台积累的角度误差不断减小。21～28 s内，角度偏差又在不断积累，当到达阈值时，位置补偿器开始主动调节旋转平台的角速度以减小旋转平台的角度误差。需要说明的是图中38～50 s内系统的补偿器虽然没起作用，但此时的角度误差也没有发生大幅度积累，这主要是因为旋转平台的角度度跟踪存在时滞和随机性，这会造成角度误差的积累存在随机性，即会出现在运行过程中角度误差的中和，需指出的是该角度的误差的中和是随机的，若仅仅靠随机中和显然是不可靠和不现实的。故必须人为的添加补偿器主动调节。

实验中角度偏差的阈值设置为Δδ=4°，此阈值可以根据在实际应用中的需求进行设置。通过本实验进一步验证了本文算法的有效性和可行性，同时利用本算法，可以保证本文的AGV能够应用于密集型仓储，即能够实现AGV对所搬运货架的位姿的调节，特别是当仓储中AGV运行通道狭小且搬运货架狭长时，通过保持货架的绝对朝向不变或调节货架的位姿，实现在搬运的过程中货架不会随AGV的运行而随意摆动，从而干涉AGV通道外是堆货区，这样即实现了AGV通道的最小化从而提高了仓库的存储密度。

4 结束语

针对AGV旋转平台的随动控制问题，提出了基于PID带位置补偿器的随动控制方法。实现对AGV运行时的角速度随动跟踪，同时为了保持AGV旋转平台的绝对位姿不变。针对角速度的跟踪，在分析AGV旋转平台的随动PID控制的优缺点的基础上引入了AGV旋转平台的随动神经PID控制，实现AGV旋转平台的运行状态发生改变时PID参数自适应更改。针对AGV旋转平台角速度跟踪过程中的角度误差积累问题，在算法上添加了位置补偿器，实现位置补偿，不致系统出现较大的误差积累。实验表明AGV旋转平台对不同的角速度都能有较好的跟踪效果，运行平稳，且系统响应时间在0.2 s以内，角度误差|θ|﹤4°。实验结果均验证了该算法的有效性和可行性。

参考文献：

[1] 郝晶晶.自动化仓储系统的设计与应用前景分析[D].合肥：中国科学技术大学，2015.

[2] 邵扬.物流业对中国经济增长的影响研究[D].长春：吉林大学，2009.

[3] WU Xing,LOU Peihuang,YU Jun,et al. Intersection recognition and guide-path selection for a vision-based AGV in a bidirectional flow network[J]. International Journal of Advanced Robotic Systems,2014,11(39):1-17.

[4] 武星,楼佩煌,唐敦兵.自动导引车路径跟踪和伺服控制的混合运动控制[J].机械工程学报, 2011, 47(3): 43-48.

[5] WU X,LOU P H,SHEN K,et al.Precise transshipment control of an automated magnetic-guided vehicle using optics positioning[J]. International Journal on Smart Sensing and Intelligent Systems, 2014, 7(1): 48-71.

[6] 巫佩军,杨文韬,余驰,等.一种用于高精度随动控制系统的轨迹预测方法[J].机电与控制学报,2014,18(7):1-5.

[7] 姜晓平,朱奕,伞冶.大功率随动实验台多永磁同步电机同步控制[J].电机与控制学报,2014,18(4):88-95.

[8] 任强,周升良，孙玉国.基于MEMS的角位置无线随动控制系统设计[J].传感器与微系统，2013,32(9):122-125.

[9] 孟文俊,刘忠强.视觉导引AGV的路径跟踪控制研究[J].控制工程，2014,21(3):321-325.

[10] 吴晓朝，吴捷，李全国.一种基于满意度的PID参数整定方法[J].华南理工大学学报，2005,33(2):39-42.

[11] 李少远，席裕庚，陈增强，等.智能控制的新进展(Ⅱ)[J].控制与决策，2000,15(2):136-140.

[12] 赵强，陈云微.基于磁流变技术的车辆座椅悬架减震研究[J].森林工程，2010,26(6):20-25.