QPSO-WT和QPSO-SVM在滚动轴承故障诊断中的应用

， ，，

(西南交通大学机械工程学院，四川 成都 610031)

0 引言

当滚动轴承发生故障时，振动信号呈现出非线性非平稳特性，小波变换是当前实现机械设备故障诊断的有效方法之一，特别适用于处理非平稳时间序列，但是由于此方法的所采用的阈值函数是分段函数，其函数连续但导数不连续，在具体的应用中不便于运算处理，限制了它的发展[1-3]。支持向量机是一个常用的机器学习方法，在实际工程中有着大量的应用[4]，但其效果却受制于惩罚参数和和函数参数的选择，轻微的差别都可能使最后的识别结果发生巨大的差异[5-6]。

QPSO算法是一种群体智能优化算法，具有控制参数少、计算简单、收敛速度快、寻优能力强、易于实现等特点，大量应用于实际优化问题求解中，并且理论上已证明其可收敛到全局最优解[7]。Gao等[8]、Lu等[9]将QPSO应用于图像处理；Fang等[10]使用QPSO优化信号处理过程；Xi等[11]，Liu等[12]使用QPSO进行参数优化。

提出一种基于小波优化阈值的滤波方法和QPSO-SVM状态识别方法，并将其应用到滚动轴承故障诊断中。实验证明，该模型能对滚动轴承故障状态作出较好的识别，从而为滚动轴承故障诊断的工业应用提供了良好的技术支撑。

1 研究方法

1.1 小波变换

Donoho提出的软阈值函数为：

(1)

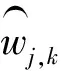
此方法可以按以下3个步骤实现：

①对观测信号f(t)作离散小波变换DWT，得到小波系数cdjk(j=1,2,…,J)，J为小波分解的尺度数。

②应用软阈值函数处理各尺度小波系数，基于所选择阈值得出各尺度小波系数的估计值。

1.2 支持向量机

SVM算法的基本思想从寻找一个最优超平面使样本集分为两类使样本离该超平面的距离最近。设有样本集D={(xi,yi)}，i=1,2,…,n,xi为第i个样本输入列向量；yi为向量机相应的输出。存在一个非线性映射函数φ(·)将样本数据映射到高维特征空间，在特征空间中找到一个最优超平面wx+b=0使得映射样本数据在精度ε下达到最优的分类效果，此时的几何间隔为γ=||w||2。在此引入松弛变量ξi，则构造最优超平面的问题转化为：

(2)

yi(ωTxi+b)≥1-ξi,i=1,2,…,n

引入惩罚参数C和拉格朗日乘子，对w，b求偏导，则可以将w和b的求解问题转换为一个凸二次规划问题：

(3)

选择适当的核函数K(xi,x)代替上式中的内积运算(φ(xi),φ(xj))，即可构造出分类函数：

(4)

1.3 量子行为粒子群算法

2004年，Sun等[13]基于Clerc等关于粒子收敛行为的研究成果，从量子力学的角度提出了QPSO算法。在量子空间中，粒子的聚集性通过粒子运动中心存在的某种吸引势产生的束缚态来描述，而处于量子束缚态的粒子可以以一定的概率密度出现在空间任何点，满足聚集态的性质的粒子可以在整个可行解空间中进行搜索，但不会发散到无穷远。

假设一个包含m个粒子的粒子群在D维解空间中飞行，在t时刻，第i个粒子位置表示为Xi(t)=[Xi,1(t),Xi,2(t),…,Xi,D(t)]，其中i=1,2,…,m。第i个粒子在D维解空间中的历史最优位置表示为Pi(t)=[Pi,1(t),Pi,2(t),…,Pi,D(t)]，群体的全局最优位置表示为G(t)=[G1(t),G2(t),…,GD(t)]，且G(t)=Pg(t)，g是全局最优位置粒子的下标，g∈{1,2,…,m}。个体最优位置的平均由下式决定：

(5)

对于最小化问题，目标函数值越小，对应的适应值越好，故第i个粒子的个体最优位置Pi(t)由下式确定：

(6)

群体的全局最优位置G(t)由下式确定：

(7)

粒子位置进化方程为：

Pi,j(t+1)=φj(t)Pi,j(t)+[1-φj(t)]Gj(t)，

φj(t)∈U(0,1)

(8)

Xi,j(t+1)=

Pi,j(t)±α·|Mbest(t)-Xi,j(t)|·ln[1/ui,j(t)]，

ui,j(t)∈U(0,1)

(9)

φj(t)，ui,j(t)为(0,1)区间均匀分布的随机数，若ui,j(t)大于0.5，α前取负号，否则取正号；单个粒子有界性的充分必要条件是α<1.782，而粒子有界性是QPSO算法收敛到全局最优解的充分必要条件，实际过程中，参数α从1.0线性下降到0.5，普遍可以取得较好的优化效果[14]。

1.4 QPSO优化小波变换(QPSO-WT)

为了克服传统小波阈值不能随着系统实时改变、仅靠人工因素和统计理论来决策的问题，提出了量子行为粒子群自适应阈值寻优算法，见图1。选用GCV风险函数作为QPSO优化小波阈值的适应函数，通过目标函数最小化来选取渐进最优阈值T。

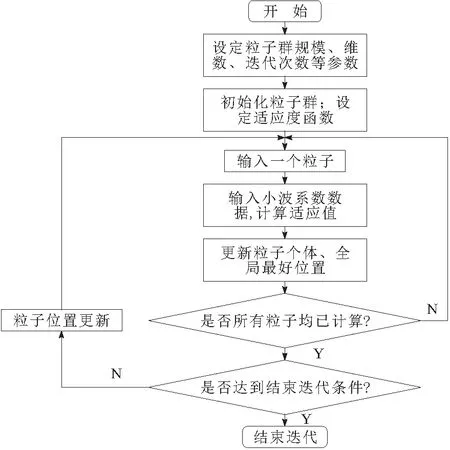
图1 QPSO-WT算法流程

1.5 QPSO优化支持向量机(QPSO-SVM)

传统的SVM需要输入惩罚参数c和核函数参数g，这两个参数与支持向量回归的预测精度息息相关。针对这种情况选用广义交叉验证(GCV)风险函数作为QPSO优化支持向量机的适应函数，通过目标函数最小化来选取渐进最优参数c和g。其流程如下。

第1步，对最佳惩罚参数和最佳和函数参数进行编码。

第2步，确定适应函数为CGV意义下的错误率。

第3步，初始化粒子群，确定迭代次数。

第4步，输入样本数据，计算粒子的适应度。

第5步，判断粒子适应度是否达到要求，如果达到要求就进行解码，如果未达到要求重新计算粒子群的平均最优位置，继续进行迭代，直至满足条件。

第6步，将解码后的最佳惩罚参数和核函数参数用来建立支持向量机模型。

第7步，利用该模型进行分类。

2 实验研究

实验数据是美国西储大学电气工程实验室的故障采样频率为48 kHz的驱动端滚动轴承故障实验数据。该实验过程共有4种不同工况，轴承故障分类如表1所示，共分为10种不同类别的轴承，总共有40组数据。

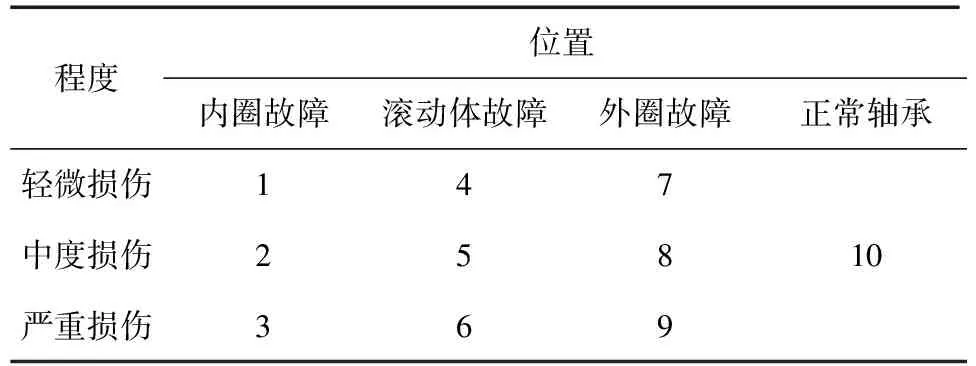
表1 滚动轴承故障分类

2.1 信号滤波

对振动信号进行5层小波降噪，选用db6小波基，QPSO优化小波阈值降噪效果见表2。

表2 QPSO优化前后软阈值滤波后的信号参数SNR与MSE

2.2 特征提取

遵循同种类别差异小，不同类别差异大的原则，选取以下13个特征参数：均方频率、重心频率、频率方差、均方根、平均信号强度、峰态系数、偏态系数、峰值、峰值因子、脉冲因子、波形因子、峭度因子、裕度系数。

按照5 ms计算一组特征的原则，得到400组特征样本，其中每个轴承类别有40个特征样本。

2.3 QPSO-SVM分类

基于1.4的算法过程，利用MATLAB平台进行编程，QPSO-SVM模型，其中设置初始种群数量为30，迭代次数为300，选择RBF核作为核函数，算法的适应度函数为CGV意义下的错误率，通过最小化适应度函数得到最优解，设置惩罚参数c的取值范围为[0,100]，核函数参数g的取值范围为[0,100]。

按照训练集和测试集都必须涵盖4种工况的原则，每种轴承类别取20个特征样本作为训练集，20个特征样本作为测试集，则得到了200个训练样本，200个测试样本。

训练集经过量子行为粒子群算法对支持向量机的输入参数进行寻优，最后得到的最佳惩罚参数为c，最佳核函数参数为g。

利用得到的最佳输入参数建立支持向量机模型，对测试集进行分类，其测试结果如图2所示，其中0～9表示10种不同的轴承状态，具体类别参照表1。从图中所示结果可以发现QPSO-SVM识别的准确率达到了87.67%，说明QPSO-SVM模型具有很高的识别精度。

图2 QPSO-SVM分类结果

为了进一步验证QPSO-SVM模型的有效性，还设计了SVM分类器和RBF神经网络分类器来对轴承故障进行分类。

在缺乏先验知识储备的情况下，SVM模型的输入参数主要依赖人为经验选择。故本次实验中设置惩罚参数c=1.4，核函数参数g=1.5。

RBF神经网络是一种应用广泛的神经网络，由于在本次实验中的特征参数为13，故设置RBF神经网络的输入层为13，输出层设为1，训练精度为1×10-6。

RBF,SVM和QPSO-SVM分类结果见表3。

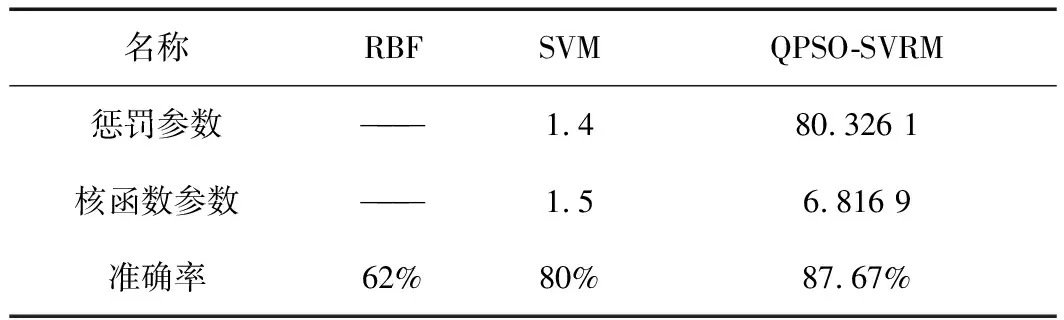
表3 RBF,SVR,QPSO-SVR诊断结果

3 结束语

首先通过对比QPSO优化后的小波降噪与普通的小波降噪发现，经过阈值寻优后的去噪效果十分明显，有着更高的SNR和更低的MSE。再对比QPSO-SVM和SVM发现，QPSO算法避免了支持向量机惩罚参数c和核函数参数g在选择上的盲目性，并且在设定的参数范围内寻找到全局最优解，具有更高的精度，同时发现QPSO-SVM有着更好的识别效果。对比QPSO-SVM和RBF神经网络发现，QPSO-SVM提高了SVM本身的识别精度，同时识别效果也高于RBF神经网络。因此在多分类的情况，QPSO-SVM模型有着更高的精度。

参考文献：

[1] PENG Z K, CHU F L. Application of the wavelet transform in machine condition monitoring and fault diagnostics: a review with bibliography [J]. Mechanical Systems and Signal Processing,2004,18:199-221.

[2] VAFAEI S,PAHNEJAT H. Indicated repeatable runout with wavelet decomposition (IRR-WD) for effective determination of bearing-induced vibration [J]. Journal of Sound and Vibration, 2003, 260: 67-82.

[3] 唐进元,陈维涛,陈思雨,等.一种新的小波阈值函数及其在振动信号去噪分析中的应用[J].振动与冲击, 2009(7): 118-121.

[4] 克里斯特安尼，等. 支持向量机导论[M]. 李国正，王猛，曾华军，译.北京: 电子工业出版社, 2004.

[5] 张小艳, 李强. 基于SVM的分类方法综述[J]. 科技信息, 2008(28): 350-351.

[6] ZHANG X Y, LIANG Y T, ZHONG J, et al. A novel bearing fault diagnosis model integrated permutation entropy, ensemble empirical model decomposition and optimized SVM[J]. Measurement, 2015, 69: 164-179.

[7] 吴涛. 粒子群及量子行为粒子群优化算法的改进研究[D]. 成都：西南交通大学,2014.

[8] GAO F,GAO H G , LI Z Q ,et al.Detecting unstable periodic orbits of nonlinear mappings by a novel quantum-behaved particle swarm optimization non-Lyapunov way[J].Chaos, Solitons & Fractals, 2009, 42(4): 2450-2463.

[9] LU Y ,LIAO Z W ,CHEN W F .An automatic registration framework using quantum particle swarm optimization for remote sensing images[R]. Proceedings of the 2007 International Conference on Wavelet Analysis and Pattern Recognition, 2007, 2: 484-488.

[10] FANG W,SUN J,XU W B. Design IIR digital filters using quantum-behaved particle swarm optimization[J]. Lecture Notes in Computer Science, 2006, 4222: 637-640.

[11] MAO L X, SUN J,WEN B X. Parameter optimization of PID controller based on quantum-behaved particle swarm optimization algorithm[J]. Complex Systems and Applications, Modeling, Control and Simulations, 2007(14): 603-607

[12] LIU J, WU Q, ZHU D Q. Thruster fault-tolerant for UUVs based on quantum-behaved particle swarm optimization[J]. Opportunities and Challenges. Springer, 2009, 214: 65.

[13] SUN J, XU W B. A Global Search Strategy of Quantum behaved Particle Swarm Optimization[R] IEEE Conference on Cybernetics and Intelligent Systems. 2004: 111-116.

[14] 孟宗,李姗姗. 小波改进阈值去噪和经验模态分解相结合的旋转机械故障特征提取[J]. 机械强度, 2014(1): 24-29.