适用于单快拍的多重信号分类改进算法

陈 涛，崔岳寒，郭立民

(哈尔滨工程大学 信息与通信工程学院，哈尔滨 150001)

0 引 言

阵列信号处理是信号处理的一个重要分支，着重于空间传输波携带信号的获取、处理和传输，即对空间分布的组传感器接收的空间传输波信号进行处理以提取信息。

波达方向(Direction of arrival，DOA)估计作为阵列信号处理中的关键问题，主要研究如何从背景噪声中估计信号的到达角信息[1]。这个领域的研究经历了几十年的发展，已经形成了比较系统的理论体系[2]。DOA估计技术在雷达、声呐、地质开发、微波无线电通讯、生物医学等领域均有广泛的应用，并取得了很大发展[3]。由于子空间算法,如MUSIC(Multiple signal classification)等可以突破瑞利极限，实现超分辨，所以近年来涌现出很多新型的基于子空间的测向算法[4，5]。

短快拍测向算法的研究主要针对军事和卫星通信，在阵列接收数据有限、目标高速运动的前提下，可以实现对目标的实时处理，并具有较高的DOA估计精度，可为高速运动目标的定位和跟踪提供技术支持[6，7]。单快拍类测向算法因其快拍数达到了短快拍的极限，属于短快拍测向算法中的特殊情况，而被单独归为一类进行研究，近年来很多专家学者将研究的目光锁向少快拍甚至单快拍下的阵列信号处理[8，9]。

DOA估计算法以高分辨MUSIC算法和ESPRIT算法为代表[10]。MUSIC算法中，通常先得到协方差矩阵，对其进行特征分解和奇异值分解后得到噪声子空间，然后利用导向矢量与噪声子空间的正交性对信号入射方向进行估计[1]。基于协方差矩阵MUSIC算法的渐近性能接近克拉美-罗界[11，12]，但无法有效地应用于单快拍情况[13，14]。

本文分析了经典MUSIC算法不适用于单快拍的原因，并对其进行了改进，提出了一种适用于单快拍的MUSIC改进(Improved-single-snapshot MUSIC，ISS-MUSIC)算法。该方法将伪协方差矩阵构造法与共轭增强法相结合，适用于单快拍，且性能优于未进行共轭增强的基于伪协方差矩阵单快拍MUSIC算法。

1 信号模型

假设K个同频不相关远场窄带信号入射到由M个全向阵元组成的均匀线阵上，信号数K已知或已经估计得到，于是阵列输出矢量为[1]：

x(t)=[x1(t),x2(t),…,xM(t)]T=As(t)+n(t)

(1)

式中：信号矢量s(t)=[s1(t),s2(t),…,sk(t)]T；噪声矢量n(t)=[n1(t),n2(t),…,nM(t)]T；导向矢量A=[a(θ1),a(θ2),…,a(θk)]，a(θi)=[1,e-jφ1,…,e-j(M-1)φi]T，φi=2πdsin(θi)/λ，θi为第i个信号的入射角度，λ为信号波长。

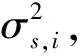
2 适用于单快拍的ISS-MUSIC算法

2.1 经典MUSIC算法不适用于单快拍的原因

在第1节的基础之上，得到阵列输出数据的协方差矩阵为：

(2)

对R进行特征分解，有：

(3)

信号子空间和噪声子空间是正交的，而信号波达方向上的阵列导向矢量在信号子空间内，所以其与噪声子空间是正交的，于是MUSIC算法通过搜索下列的极大值点来估计信号DOA[15]：

(4)

实际应用中，只能得到协方差矩阵R的估计值R′(称为采样协方差矩阵)，通常取：

(5)

式中：L为快拍数。

对R′进行特征分解后可得噪声子空间的估计值G′，此时搜索下列的极大值点来估计信号DOA：

(6)

如果只有一个快拍可用，由式(5)可知，采样协方差矩阵的秩为1，而信号子空间的秩是大于信号数的，此时利用R′的特征分解无法区分出信号子空间和噪声子空间，因此经典MUSIC算法不适用于单快拍[16]。

2.2 伪协方差矩阵构造方法

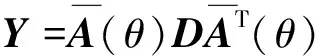
矩阵Y的元素Y(p,q)可表示为：

exp{-j[φω+(q-1)Δφω]}dnω

(7)

式中:dnw为矩阵D的元素。

其中，矩阵中的可利用信息可表示为如下形式：

(8)

当矩阵D为对角阵时，式(7)可表示为：

(9)

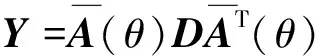
由式(8)可知，M个阵列接收信号的相位是位于[φn,φn+(M-1)Δφn]范围内的等差数列，可表示的相位范围为(M-1)Δφn，固定相位φn的取值与相位参考点的选择有关。这就是构造伪协方差矩阵时可用的信息。

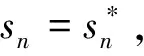
(10)

式(10)的相位是位于[-φn,-φn-(M-1)Δφn]范围内的等差数列，这相当于增加了可利用的信息量。

基于以上理论，令L=M、φn=0、dnn=sn并代入式(9)，此时伪协方差矩阵可表示为[17]：

(11)

2.3 共轭增强法

为进一步提高算法性能，充分利用阵列输出数据的共轭信息，在式(11)的基础上，构造以下伪协方差矩阵[18]：

Y′=[Y,JY*J]

(12)

式中：J为交换矩阵，其反对角线元素为1，其他元素为0。

由式(12)可知，此方法将M×M维伪协方差矩阵拓展为M×2M维。

对拓展的伪协方差矩阵进行二阶积累，公式如下[16]：

(13)

2.4 ISS-MUSIC算法的步骤

综上所述，将2.2节与2.3节提出的方法进行合并为ISS-MUSIC算法，其步骤如下：

步骤1 利用式(11)得到伪协方差矩阵Y。

步骤2 利用式(12)得到共轭增强后的伪协方差矩阵Y′。

步骤3 求伪协方差矩阵的二阶积累：

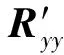
步骤5 搜索谱函数:

的极大值点确定信号入射方向。

3 仿真试验及性能分析

3.1 ISS-MUSIC算法分辨能力

仿真条件：均匀线阵的阵元数为8；阵元间距为半波长；快拍数为1；信噪比为10 dB；入射角分别在0°～10°和50°～60°随机产生。ISS-MUSIC算法的空间谱图如图1所示，图中的两条竖线为原入射角度。由图1可知，ISS-MUSIC算法具有较好的信号分辨能力。

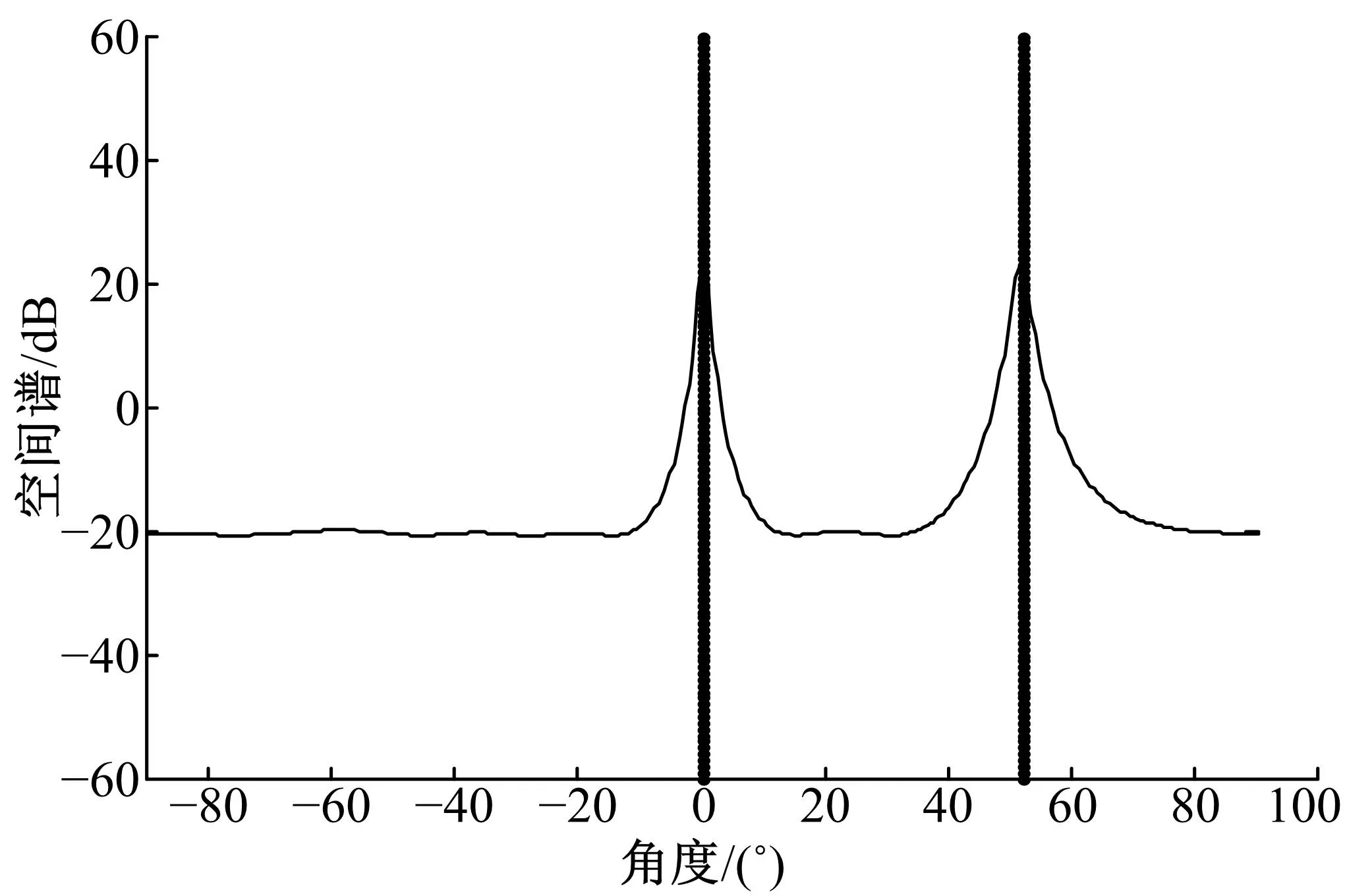
图1 ISS-MUSIC的空间谱图Fig.1 Space spectrum of ISS-MUSIC

3.2 测角精度比较

将ISS-MUSIC算法与未进行共轭增强的基于伪协方差矩阵单快拍MUSIC算法进行性能比较。仿真中，均匀线阵的阵元数为8；阵元间距为半波长；快拍数为1；入射角在0°～90°随机产生。两种算法随信噪比变化的测向精度如图2所示。

由图2可知，ISS-MUSIC算法的测向精度高于未进行共轭增强的基于伪协方差矩阵单快拍MUSIC算法的测向精度。

图2 测向精度Fig.2 Accuracy of DOA

4 结束语

提出了一种单快拍下的测向算法。该算法对经典MUSIC测向算法进行了改进，将伪协方差矩阵构造法与共轭增强法相结合。仿真试验结果表明：ISS-MUSIC算法在单快拍的条件下有较好的信号分辨能力，且测向精度优于未进行共轭增强的基于伪协方差矩阵单快拍MUSIC算法。

参考文献：

[1] 王永良,陈辉,彭应宁,等. 空间谱估计理论与算法[M]. 北京：清华大学出版社,2005.

[2] Zeng Hao, Ahmad Z,Zhou Jian-wen. DOA estimation algorithm based on adaptive filtering in spatial domain[J]. China Communication,2016,12(13):49-58.

[3] 李新波,石要武,马彦，等. 基于RARE-cumulant的互耦矫正和DOA估计[J]. 吉林大学学报：工学版,2010,40(4):1118-1121.

Li Xin-bo,Shi Yao-wu,Ma Yan,et al. Mutual coupling calibration and direction of arrival estimation based on RARE-cumulant algorithm[J]. Journal of Jilin University(Engineering and Technology Edition),2010,40(4):1118-1121.

[4] Forster P,Ginolhac G,Boizard M. Derivation of the theoretical performance of a Tensor MUSIC algorithm[J]. Signal Processing,2016,129(1):97-105.

[5] Kintz A L,Gupta I J. A modified MUSIC algorithm for direction of arrival estimation in the presence of antenna array manifold mismatch[J]. IEEE Transactions on Antennas and Propagation,2016,64(11):4836-4847.

[6] Tervo S. Single snapshot detection and estimation of reflections from room impulse responses in the spherical harmonic domain[J]. IEEE-ACM Transactions on Audio Speech and Language Processing,2016,24(12):2466-2480.

[7] Chen Chun-hui, Zhang Qun, Gu Fu-fei. 2D single snapshot imaging using MIMO radar based on SR[J]. Electronics Letters,2016,52(23):1946-1948.

[8] Elbir A M, Tuncer T. 2-D DOA and mutual coupling coefficient estimation for arbitrary array structures with single and multiple snapshots[J]. Dignal Signal Processing,2016,54:75-86.

[9] 王凌,李国林. 利用单次快拍实现相干信源二维测向的新算法[J]. 北京理工大学学报，2015，35(5):512-518.

Li Ling,Li Guo-lin. A new algorithm of 2D DOA whose source is coherent with single snapshot[J]. Journal of Beijing Institute of Technology,2015,35(5):512-518.

[10] 李新波,李晓青,刘国君,等. 用于声矢量阵列波达方向估计的四元数最小范数法[J]. 光学精密工程,2014,22(7):1969-1975.

Li Xin-bo,Li Xiao-qing,Liu Guo-jun, et al. Quaternion min-norm algorithm for DOA estimation with acoustic vector sensor array[J]. Optics and Precision on Engineering,2014,22(7):1969-1975.

[11] Stoica P, Nehorai A. MUSIC maximum likelihood, and Cramer-Rao bound[J]. IEEE Transactions on Acoustics, Speech,and Signal Process,1989,37(5):720-741.

[12] Suryapakash R T, Nadakuditi R R. Consistency and MSE performance of MUSIC-based DOA of a single source in white noise with randomly missing data[J]. IEEE Transactions on Signal Processing,2015,63(18)：4756-4770.

[13] Liao W, Fannjiang A. MUSIC for single-snapshot spectral estimation: stability and super-resolution[J]. Applied and Computational Harmonic Analysis,2016,40(1):33-67.

[14] Hacker P, Yang B. Single snapshot DOA estimation[J]. Advances in Radio Science,2010,8(1921):251-256.

[15] Roy R, Kailath T. ESPRIT-estimation of signal parameters via rotational invariance techniques[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing,1989,37(7):984-995.

[16] 刘剑,宋爱民,余侃民,等. 适用于任意快拍数的MUSIC算法[C]∥2016全国电子战学术交流大会.北京:中国电子学会,2016:562-567.

[17] 谢鑫,李国林,刘华文. 采用单次快拍数据实现相干信号DOA 估计[J]. 电子与信息学报,2010,32(3):604-608.

Xie Xin,Li Guo-lin,Liu Hua-wen. DOA estimation of coherent signals using one snapshots[J]. Journal of Electronics & Information Technology,2010,32(3):604-608.

[18] Wen Zhong,Li Li-ping,Wei Ping. Fast direction finding using modified pseudocovariance matrix[J]. IEEE Transactions on Antennas Propagat,2006,54(12):3914-3918.