三厢轿车多参数气动优化
2018-06-01李启良曹冠宁杨志刚钟立元
李启良,曹冠宁,李 璇,杨志刚,钟立元
(1.同济大学 上海地面交通工具风洞中心,上海 201804;2.同济大学 上海市地面交通工具空气动力与热环境模拟重点实验室,上海 201804)
0 引 言
汽车的气动阻力由内部和外部阻力组成。无论是传统内燃机汽车还是新型电动汽车都需要外部气流进入前舱将发动机、空调等热量带到车外。在满足散热性能的同时,不可避免地产生内流阻力。在汽车开发时,如不考虑内流直接进行车身气动优化,可能得到优化外形并不是真实状态的最佳气动外形。因此有必要将内流作为约束进行车身气动优化。
早期车身气动优化主要基于道路试验和风洞试验。随着数值方法和计算机硬件的发展,数值仿真已全面应用于车身气动优化中。车身气动优化包括单一参数的优化和多参数优化。单一参数优化比较简单和直观。刘湘云等[1]通过数值仿真研究了前车窗角度变化对车身气动性能的影响,寻找到研究车型的最佳前车窗角度。车身是由多参数组成,各参数之间也会相互影响。为此研究人员从单一参数扩展到两个及以上参数。Khondge等[2]通过网格变形方法,对前、后风窗倾角和侧窗内倾角进行气动优化,寻找到最佳倾角组合。Magazoni等[3]使用伴随优化方法进行后视镜外形优化,获得低阻后视镜外形。郭建成等[4]针对轿车的前阻风板的安装位置和高度建立Kriging近似模型,通过多岛遗传算法进行全局寻优,明显改善了轿车的气动性能。容江磊等[5]将Kriging近似模型与带精英策略的非支配排序遗传算法相结合,对跑车尾翼的断面形状进行气动优化设计,取得良好的优化效果。
随着油耗要求提高,迫切需要从整车角度进行多参数优化,以获得更低阻力的车身外形。Han等[6]首先采用稳态流动计算和伴随优化方法对整车6个区域进行气动优化,获得优化外形,然后使用涡分离模型对该优化外形进行瞬态流场分析。Sun等[7]采用响应面方法对早期开发阶段的运动多功能汽车进行气动外形优化,得到比原始气动阻力系数低0.018的最优外形。Lundberg等[8]通过神经网络和进化优化方法全自动地进行汽车外形优化,得到最优模型的气动阻力比原始模型降低13%。所在课题组在过去几年开展了多参数建模和遗传算法相结合的低阻车身气动优化研究,得到气动阻力系数仅为0.129的低阻车身等一系列研究成果[9,10]。
回顾已有研究发现,绝大多数的车身气动优化都不含内流,优化外形可能并不是真实状态的最佳外形。为此,本文结合了数值仿真和风洞试验,建立三厢轿车的内流简化模型和参数化模型,基于遗传算法进行气动优化,获得带内流约束的优化外形。
1 风洞试验方法
选用手动挡的三厢轿车作为研究对象,该车的长、宽和高分别为4521、1788和1492 mm。整车放置在气动-声学整车风洞的6分量气动天平中。通过天平测量整车受到的气动力,通过叶轮式风速仪得到风扇在不转时通过散热器的风量,如图1所示。试验速度从80 km/h增加到160 km/h,以20 km/h为间隔。所有试验均开启边界层抽吸和移动带,车轮处于旋转状态。

图1 气动力和进气量测量Fig.1 Aerodynamic force and air input measurement
2 数值计算方法
2.1 整车数值仿真
创建长、宽和高分别为9倍车长、10倍车宽和4倍车高的虚拟风洞。整车模型放置在虚拟风洞的地面上,车头距离计算域的进口3倍车长。
使用Hypermesh进行计算域内部件面网格的生成。车身外表面基于自身流动特征合理布置面网格大小。后视镜和A柱区域,网格大小为5 mm;在后风窗和车尾的流动分离区域,网格大小为6 mm;底盘和前后轮的网格大小分别为15 mm和10 mm;发动机舱中发动机、变速箱、冷却部件等众多零部件,网格大小为5 mm;其他区域,网格大小约为10 mm。基于以上网格大小,整个计算域共创建319万个面网格。
使用Star-CCM+软件生成共2100万个体网格。体网格类型为Trimmer网格,并在车身所有壁面和地面布置边界层网格,以满足非平衡壁面函数对y+的要求。为了能够更精确地模拟整车流动情况,在计算域内分别设置了3个加密区,图2为计算域中间截面网格。
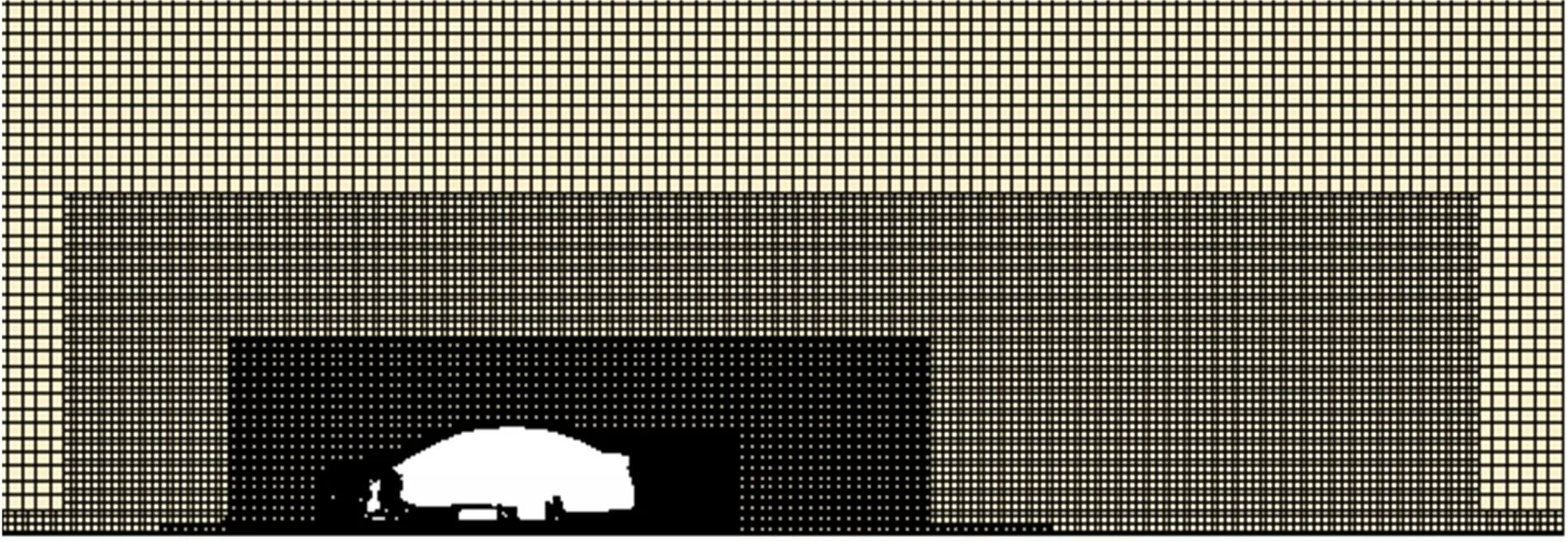
图2 计算域中间截面网格Fig.2 Middle-section mesh of computational domain
为了建立三厢轿车参数化模型,有必要对内流进行简化,从而更好地实现外形参数的优化,减少单个样本点的计算时间,提高优化效率。内流简化需要保证简化模型的进气量与实车相同。为此,建立了与真实车辆相同的开口面积,保留原有冷却模块,如图3所示。从图3可以看出,内舱绝大多数部件被删除,前端进气通过内部流道经冷却模块后直接流出到车底。

图3 简化模型Fig.3 Simplified model
仍使用Star-CCM+软件对简化内流模型生成Trimmer体网格,体网格总数为1800万个。体网格生成的所有设置与未简化的整车模型相同。
计算域入口为速度入口,对应车速为120 km/h。出口为压力出口,设为0 Pa。两个侧面和顶面设为对称面,地面设定为移动壁面,车轮设置为旋转壁面。冷却模块采用多孔介质模型,其阻力特性由试验提供,冷凝器和散热器的阻尼系数,如表1所示。为了实现简化模型的进气量与原来实车一致,需要改变冷却模块的阻尼系数来调整进气量。简化模型气动计算方法与真实模型完全相同,只是冷却模块阻尼系数值不同。

表1 冷凝器和散热器参数Table 1 Parameters of condenser and radiator
选用k-ε两方程湍流模型[11],采用二阶精度计算3000步后,残差降到10-4并且监测到气动阻力系数Cd值没有明显变化时,可以认为计算结果收敛。每个计算工况在24核的惠普刀片服务器上需计算24 h。本文约有20个计算工况,完成所有计算需480 h。
2.2 多参数优化方法

图4 设计变量Fig.4 Design variable
基于建立的简化内流轿车模型,选取图4所示的6个设计变量。结合原始参数和工程经验,确定如表2所示的参数变化范围。

表2 优化参数Table 2 Optimization parameters
利用CATIA软件建模,根据6个设计变量确定车身上需要重建几何模型的部分,在这些部分创建了628个控制点、127条样条曲线、79个几何曲面,使之与原始几何形状保持一致。利用样条曲线捕捉描绘原始几何模型的轮廓特征,由样条曲线填充生成的曲面高度逼近原始几何形状,并允许曲面随着样条曲线形状的改变而改变。样条曲线的形状由控制点控制,6个设计参数为独立变量,控制点的坐标是因变量,通过设计变量与因变量之间的映射最终建立了378个函数关系式。通过改变参数水平,使控制点的坐标随着函数关系式而相应改变,从而改变样条曲线的形状,生成新的曲面造型,最终得到满足不同参数水平的车身形状,成为车身优化的样本点。图5为重建后的几何形状。
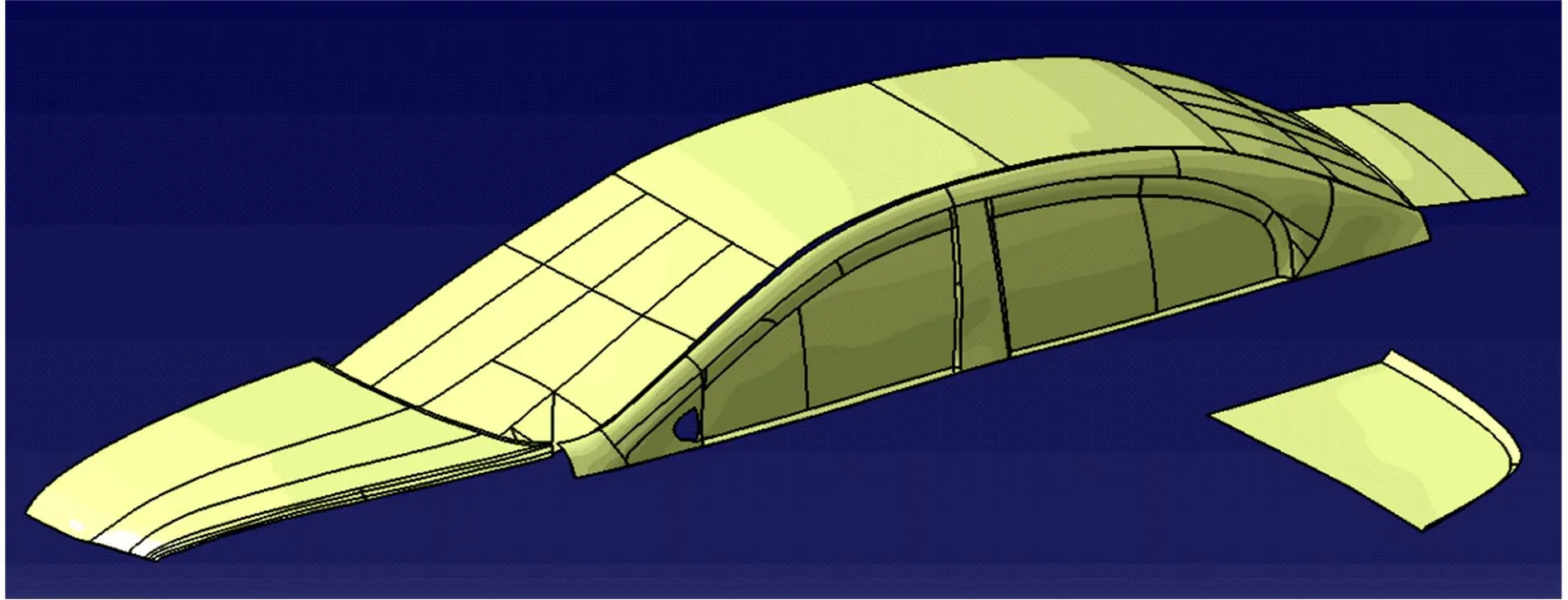
图5 重建后的几何形状Fig.5 Reconstructed geometry
对6个设计变量进行参数组合,由于车型本身的限制,后挡风玻璃倾角c与行李箱盖倾角d的变化一致,只需要其中1个参数的变化值即可。对每个变量进行选择并组合,首先通过优化拉丁方设计(Latin square design)[12]的方法确定参数组合,然后根据设计变量组合修改参数化模型得到多个模型。由于车身几何较复杂,处理每个模型需要消耗大量的时间,受时间和计算资源的限制,第一代选取10组参数组合进行计算。然后通过以下两种遗传算法对第一代的结果进行优化选择。
(1)轮盘赌选择法

(2)Taguchi方法
鲁棒性参数设计(RPD)是一种获得可控参数水平的方法,可用于将输出平均值设置在期望目标处,并使该目标值的周围变化达到最小值。
Taguchi方法提供了一些规则去简化和标准化试验设计,这个方法的关键是使用统计方法设计试验,以找到整个群体的最佳参数。使用一组正交阵列设计试验,并且同时进行,此时使用正交阵列会显著减少所需试验的数量。Taguchi方法使用信噪比(SNR)分析试验结果,SNR是信号变量与噪声变量的比率。SNR分析的目的是确定变量的最佳组合以获得最佳响应量,其定义为:
SNR=-10logδ
(1)
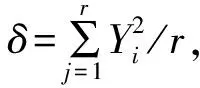
由于每个参数水平下会有数个样本,通过求取SNR,可以得到对于每个参数SNR随参数水平的变化。根据SNR曲线,对于每个参数均可以挑选出的一个最佳水平。
3 结果分析及讨论
3.1 气动仿真与试验结果对比
在风速为120 km/h时,未简化的整车模型的气动阻力系数的数值仿真值和试验值分别为0.358和0.335,误差约为7%;它们的进气量分别为1.38 m3/s和1.30 m3/s,误差约为6%。
经多轮计算和调整,确定简化模型冷却模块的阻尼系数为45.26 kg/m4,黏性阻尼系数为112.55×105kg/(m3s)。此时简化模型的气动阻力系数为0.311,进气量为1.39 m3/s,实车模型的气动阻力系数为0.358,进气量为1.38 m3/s。之所以简化模型的气动阻力系数比实车模型小,是因为大多数内舱部件被删除,底盘拉平。
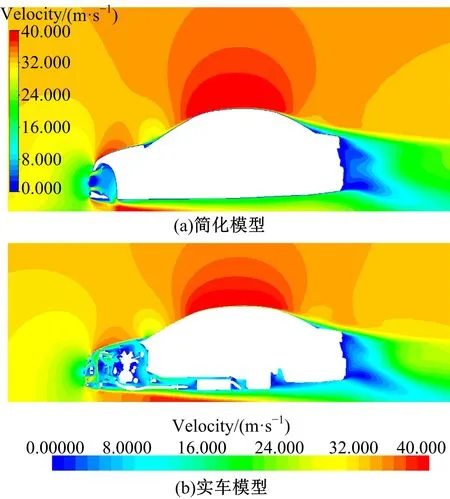
图6 中截面速度云图Fig.6 Mid-section velocity contour
图6为简化模型和实车模型的中截面速度云图,两图中最大速度和最小速度的分布区域基本一样。简化模型的底盘部分被拉平,相较于实车模型,车身下方的速度会稍高。气流流过车底,由于速度较高,使得简化模型的车尾部的气流滞留,低速区的范围比实车模型稍大。总体来看,简化内舱和底盘对车身周围速度的影响较小。
从以上对比结果可见,虽然简化后模型的气动阻力系数比实车模型小,但是简化模型与实车模型的流动结构相差非常小,且简化模型的进气量与实车模型一致,可使用简化模型进行多参数气动优化。
3.2 多参数气动优化结果
表3给出了基于优化拉丁方设计方法创建的第1代参数组合及计算结果。从第1代10组模型的计算结果中挑选出结果最好的5组参数进行轮盘赌选择,通过产生随机数,经过25轮选择后得到下一代5组参数组合并进行计算,得到第2代的计算结果,见表4。由第2代5组模型的计算结果可以发现:这5组模型优化的效果并不明显,气动阻力系数均下降得很缓慢,与上一代较好的模型相比,气动阻力并没有明显改善。

表3 第1代参数组合及计算结果Table 3 The first generation of parameter combinations and calculation results

表4 第2代参数组合及计算结果Table 4 The second generation of parameter combination and calculation results
利用Taguchi方法进行优化,基于第1代10组参数组合的仿真结果,由式(1)计算出每组的SNR值。Taguchi方法的结果由每个参数各个水平和SNR平均值的散点图提供。每个参数水平的SNR平均值由相应参数的每个水平的SNR之和除以该水平下相应参数的数量而得到。根据图7可以确定每个参数的最佳值,基于“响应值越小、结果越理想”的原则,同时考虑方程为负相关函数,确定最终每个参数的最大值为整车气动阻力系数的最佳水平。
SNR平均值的最大值对应的设计参数组合即为最佳组合。根据该优化方法得到的最佳参数组合重新修改几何模型,并进行仿真计算,表5给出了最佳组合和原始模型的参数组合及计算结果。由表5中可以看出,得到最佳组合的气动阻力系数为0.298,比原始值降低了4.2%。
通过以上遗传算法的优化过程,发现Taguchi方法优化过程快速且效果也较好,故将Taguchi方法优化的结果定为最佳优化结果。图8给出了最佳优化模型和原始模型的各设计变量参数。由表5和图8可以看出,优化后的模型变化较明显的是尾部行李箱盖倾角和离去角,均有向内收缩的趋势。其他变量的倾角变化约为1°~2°。
下面分别利用Pareto图(见图9)和流场云图(见图10)对这两个模型进行分析。图9为Pareto图,目标函数为气动阻力系数,它受到各个设计变量的综合影响。从图9可以看出:车尾部离去角e对气动阻力系数的影响最大,并与该目标函数呈现负相关关系。
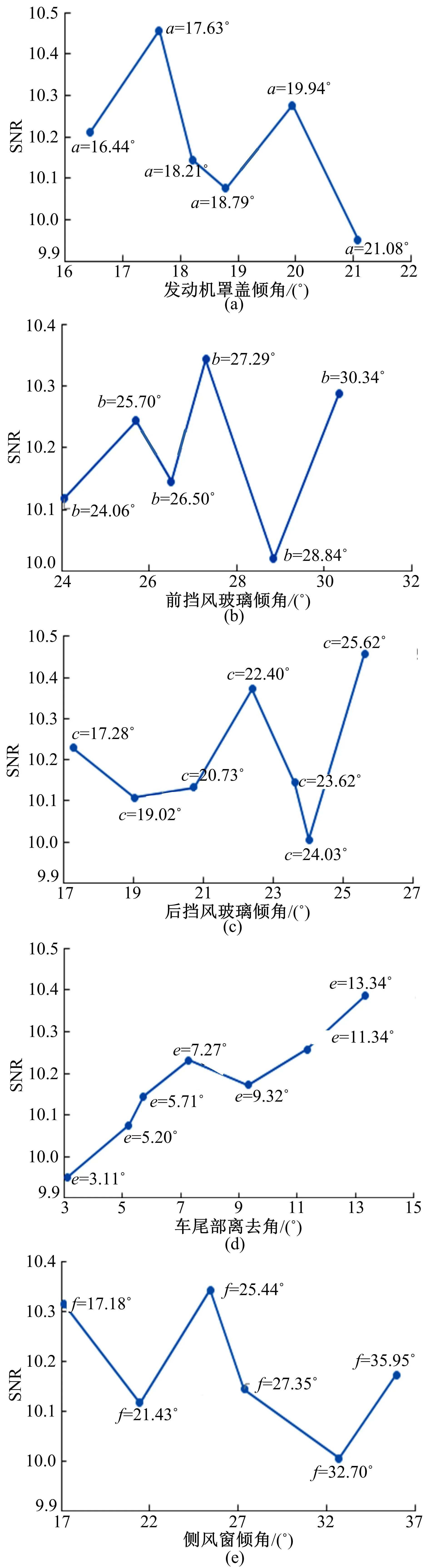
图7 各个参数与SNR的散点图Fig.7 Scatter plot of each parameter and SNR

表5 原始模型与最佳模型的参数对比Table 5 Parameters comparison of the original model and the best model
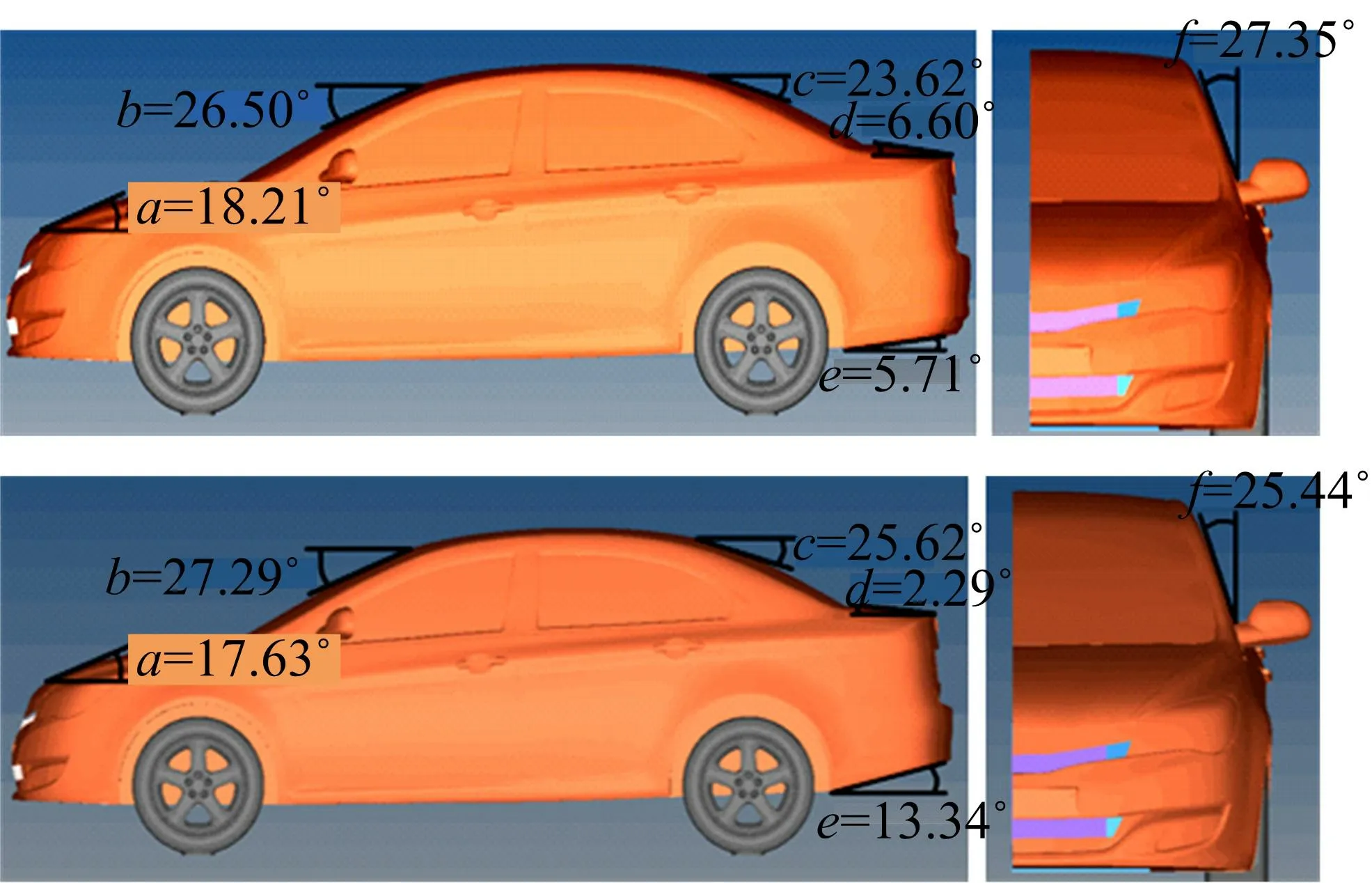
图8 各设计变量参数示意图Fig.8 Schematic diagram of each design variable

图9 目标函数的Pareto分析Fig.9 Pareto analysis of objective function

图10 尾部速度矢量图Fig.10 Velocity vector of vehicle wake
除了单一变量对目标函数有影响之外,还有“侧风窗倾角f-发动机罩盖倾角a”、“侧风窗倾角f-前挡风玻璃倾角b”这些变量的交互作用对目标函数的影响也较大,值得关注。
图10为模型尾部的速度矢量图,图中用方框标出了尾涡的位置。从图中可以看出:从原始模型到优化模型,上、下2个涡的位置均向后方移动。涡流区中心的后移能够适当降低车尾受到尾涡的影响,提升了车尾压力,降低了气动阻力系数。
4 结 论
(1)通过比较三厢轿车气动阻力系数和进气量的仿真与试验结果发现,当速度为120 km/h时,两者气动阻力系数分别为0.358和0.335,进气量分别为1.38和1.30 m3/s,两者差异均较小,表明本文数值仿真方法是正确、可行的。
(2)建立了三厢轿车内流简化模型,它与实车模型前端进气量几乎相等,流动结构基本一致,可用于建立多参数气动优化模型,降低了建模难度,缩短了优化时间,提升了优化效率。
(3)建立了带内流的三厢轿车参数化模型,通过Taguchi方法得到最优模型,其气动阻力系数为0.298。相比原始模型,气动阻力下降了4.2%。对比优化模型与原始模型,发现车尾部的参数变化较大,处于车头和车中部分的设计参数改变幅度较小。
参考文献:
[1] 刘湘云,冯俊虎,郑智贞,等. 不同前车窗角度对汽车动力性能影响的数值模拟[J]. 北京工业大学学报,2009,35(7):987-990.
Liu Xiang-yun,Feng Jun-hu,Zheng Zhi-zhen,et al. Effect of different front window angles on the automobile dynamic performances[J]. Journal of Beijing University of Technology,2009,35(7):987-990.
[2] Khondge A,Sovani S,Verma G. Automation of vehicle aerodynamic shape exploration and optimization using integrated mesh morphing and CFD[C]∥SAE Paper,2011-01-0170.
[3] Magazoni F,Buscariolo F,Maruyama F,et al. Aerodynamic shape improvement for driver side view mirror of hatchback vehicle using adjoint optimization method[C]∥SAE Paper,2015-36-0156.
[4] 郭建成,谷正气,容江磊,等. 基于Kriging模型的某轿车前轮阻风板优化[J]. 郑州大学学报:工学版,2011,32(3):125-128.
Guo Jian-cheng,Gu Zheng-qi,Rong Jiang-lei,et al. Optimization of air dam skirts of the front-wheels of a car based on kriging model[J]. Journal of Zhengzhou University(Engineering Science),2011,32(3):125-128.
[5] 容江磊,谷正气,杨易,等. 基于Kriging模型的跑车尾翼断面形状的气动优化[J]. 中国机械工程,2011,22(2):243-247.
Rong Jiang-lei,Gu Zheng-qi,Yang Yi,et al. Aerodynamic optimization of cross sectional shape for a sports car′s rear wing based on kriging surrogate model[J]. China Mechanical Engineering,2011,22(2):243-247.
[6] Han T,Kaushik S,Karbon K,et al. Adjoint-driven aerodynamic shape optimization based on a combination of steady state and transient flow solutions[C]∥SAE Paper,2016-01-1599.
[7] Sun S,Chang Y,Fu Q,et al. Aerodynamic shape optimization of an SUV in early development stage using a response surface method[C]∥SAE Paper,2014-01-2445.
[8] Lundberg A,Hamlin P,Shankar D,et al. Automated aerodynamic vehicle shape optimization using neural networks and evolutionary optimization[C]∥SAE Paper,2015-01-1548.
[9] 韦甘,杨志刚,李启良. 低阻车身形体的参数化建模与气动试验[J]. 同济大学学报:自然科学版,2014,42(5):769-772,781.
Wei Gan,Yang Zhi-gang,Li Qi-liang. A parametric modeling method of low-drag car body and aerodynamic test[J]. Journal of Tongji University (Natural Science), 2014,42(5):769-772,781.
[10] 韦甘,杨志刚,李启良. 基于分步遗传算法的车身气动优化[J]. 吉林大学学报:工学版,2014,44(6):1578-1582.
Wei Gan,Yang Zhi-gang,Li Qi-liang. Aerodynamic optimization method for car body based on process costing genetic algorithm[J]. Journal of Jilin University(Engineering and Technology Edition),2014,44(6):1578-1582.
[11] Shih T H, Liou W W, Shabbir A, et al. A newk-εeddy viscosity model for high Reynolds number turbulent flows: model development and validation[J]. Computers and Fluids,1995,24(3):227-238.
[12] Mckay M D, Beckman R J, Conover W J. Comparison of three methods for selecting values of input variables in the analysis of output from a computer code[J]. Technometrics,1979,21(2):239-245.
