基于改进和声搜索算法的越库车辆排序
2018-06-01王占中刘晓峰赵利英
王占中,卢 月,刘晓峰,赵利英
(1.吉林大学 交通学院,长春 130022;2.吉林省运输管理局,长春 130022)
0 引 言
越库是产品在物流环节中,不经过中间仓库或站点,直接从一个运输工具换载到另一个运输工具的物流衔接过程。越库系统可以在短时间内处理大量物品,加快库存周转速度,减少库存需求空间和客户响应时间,在控制物流成本的同时,提高客户服务水平。
目前,研究人员在越库场景和求解目标方面展开广泛的研究。如:Yu等[1]根据越库门的数量、是否有临时库存与集送货车辆进出的次数提出32种越库组合方法,并着重研究带有临时库存的单集、送货门的越库模型。Yu[2]在先前研究的基础上,进一步研究了多集货门及送货门的越库模型。Madani-Isfahani等[3]以运作时间作为目标函数建立了多越库门的越库模型。Mohtashami[4]建立了允许送货车辆反复进出装货平台的越库模型,在车辆交换时间较短的情况下有较好的表现。
在求解方面,以智能算法为主,较为典型的有禁忌搜索算法、模拟退火算法和遗传算法等。Madani-Isfahani等[3]通过萤火虫算法求得的越库车辆序列比模拟退火算法求得的序列运作时间短。Arabani等[5]建立了带有临时库存的单集、送货门的越库模型,采用多种智能算法(如遗传算法、蚁群算法与粒子群算法等)求解相应问题。Soltani等[6]运用模拟退火算法和混合变量邻域搜索算法求解大规模的越库车辆排序问题。Assadi等[7]建立混合线性规划模型,采用模拟退火算法和遗传算法求解相应问题。缪朝炜等[8]采用自适应遗传算法求解带有车辆容量限制以及时间窗约束的越库车辆排序问题。
和声搜索算法作为新兴的启发式算法,具有概念容易理解、抽样简单和参数变量少的优点。针对当前研究存在的不足,本文将和声搜索算法用于越库车辆排序问题的优化求解。
1 描述及模型设计
1.1 问题描述
假设越库系统仅有一个卸货平台和一个装货平台,在装货平台前存在临时库存。当到达装货平台的货物与当前送货车辆的需求不匹配时,物品可以存储在临时库存中,等到合适的送货车辆进入卸货平台后再将货物进行装载。越库系统作业流程如图1所示。

图1 越库作业流程图Fig.1 Flow chart of cross docking
1.2 数学模型
建立模型前需进行如下假设:
(1)所有的集、送货车辆都可以被使用,且集、送货作业可以同时进行。
(2)禁止送货车辆同时从集货车辆和临时库存装货。
(3)临时库存大小没有限制,但物品不允许长期存储于临时库存中。
(4)每种类型的集货物品总数等于每种类型的送货物品总数。
(5)集货车辆所装载的不同类型的物品卸货顺序可以随意确定。
(6)送货车辆物品装货顺序与集货车辆物品卸货顺序保持一致。
(7)所有集、送货车辆因交替装卸货所导致的延迟时间一致。
(8)所有物品从集货平台到装货平台的移动时间相等。
(9)集、送货车辆每次只能卸载或装载一个物品,物品装卸货均耗1单位时间。
本文以越库作业完工时间T为目标函数建立数学模型,首先对建模所需数学符号做如下定义:T为总运作时间;ci为集货车辆i进入集货平台的时刻;Fi为集货车辆i离开集货平台的时刻;dj为送货车辆j进入装货平台的时刻;Lj为送货车辆j离开装货平台的时刻。vij=1表示有物品从集货车辆i移动到送货车辆j,vij=0表示其他情况。pij=1表示在集货车辆序列中集货车辆i排在集货车辆j之前,pij=0表示其他情况。qij=1表示在送货车辆序列中送货车辆i排在送货车辆j之前,qij=0表示其他情况。R为集货车辆数;S为送货车辆数;N为物品种类数;rik为最初装载在集货车辆i中的k物品总数;sjk为最初送货车辆所需要k物品的总数;D为因装卸货车辆交替所耽搁的时间;V为物品从集货平台到装货平台移动时间;xijk为集货车辆i转移物品k到送货车辆j的数量;M为较大正实数。
目标函数P0为:
minT
s.t.T≥Lj,j∈∀
(1)
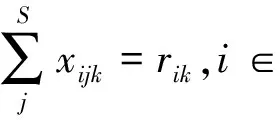
(2)
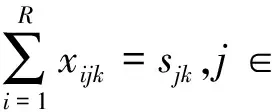
(3)
xijk≤Mvij,i∈∀,j∈∀,k∈∀
(4)
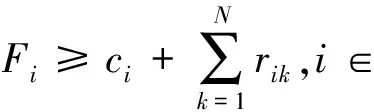
(5)
cj≥Fi+D-M(1-Pij)
(6)
i∈∀,j∈∀,i≠j
ci≥Fj+D-Mpij
(7)
pii=0,i∈∀
(8)
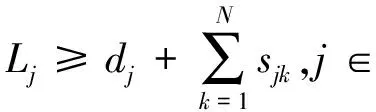
(9)
dj≥Li+D-M(1-qij)
(10)
i∈∀,j∈∀,i≠j
di≥Lj+D-Mqij
(11)
i∈∀,j∈∀,i≠j
qii=0,i∈∀
(12)
i∈∀,j∈∀
(13)
以上所有变量均大于等于零。
集货车辆货品一部分直接搬送到送货车辆上,一部分暂存于临时库存中。货品直接转移到送货车辆上比转移到临时库存后再转移到送货车辆上所需时间少。为此,货品转移到临时库存中的数量越少,总越库作业所需时间越少。储存在临时库存中的物品数量多少由集、送货车辆之间的排序引起,因此集、送货车辆排序的优劣可以通过临时库存中物品数量的多少判断。
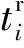
目标函数P1为:
(14)
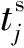
(15)
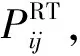
(16)
(17)
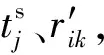
(18)
2 改进的和声搜索算法
2.1 和声搜索算法求解过程
和声搜索(Harmony search,HS)算法由Geem等于2001年提出[9]。首先在和声解集HM内随机生成HMS组初始解,然后以记忆库取值概率HMCR选择是在HM内搜索新解,还是在和声记忆库外取值。若解来自于HM内,则需依据音调调整概率PAR选择是否对新解作频宽BW大小的局部扰动。最后,判断新解目标值是否优于HM内的最差解。若是,则用新解替换最差解,继续迭代,直至满足终止条件为止。
2.2 改进的和声搜索算法
基本的和声搜索算法其参数是固定的,但参数在不同迭代时期有不同的表现形式。例如,在迭代初期较大的BW搜索较优结果的能力较好,但在迭代末期较小的BW有更好的表现[10,11]。为提高HS算法的搜索能力,IHS算法在音调调整步骤对PAR和BW做动态调整。BW和PAR的计算过程如式(19)(20)(21)所示:
PAR(gn)=
(19)
BW(gn)=BWmaxexp(c×gn)
(20)
(21)
式中:PAR(gn)、BW(gn)分别为每一次迭代的PAR和BW的值;PARmax、PARmin分别为PAR的最大值和最小值;BWmax、BWmin分别为BW的最大值和最小值;gn为迭代次数;NI为总迭代次数。
2.3 参数设定
田口试验被广泛地应用于工程设计中,用来确定最优的试验条件。每个参数的影响能力可以通过信噪比(Signal to noise ratio,SNR)表示,通过SNR在控制因子中寻找变异量小的组合。根据HS算法和IHS算法参数特点,设置不同参数水平如表1和表2所示。以试验组1中数据为基础,通过MINITAB软件得到两种算法的参数在不同水平下的信噪比主效应图如图2和图3所示。
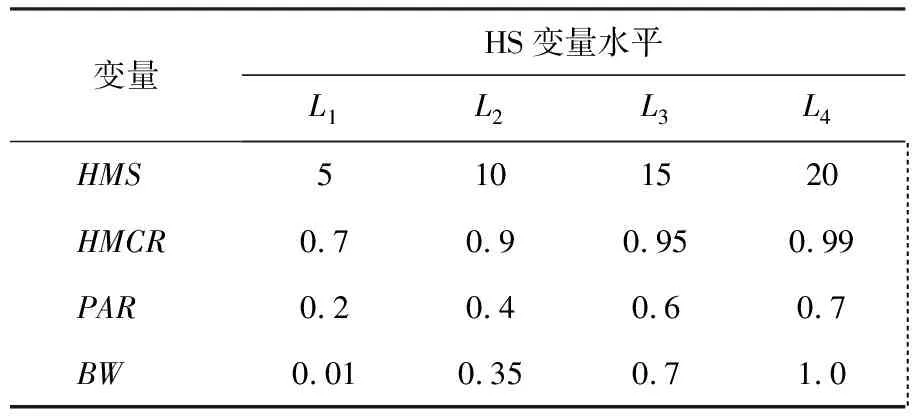
表1 HS算法的因子及其水平Table 1 Levels of parameters for HS

表2 IHS算法的因子及其水平Table 2 Levels of parameters for IHS
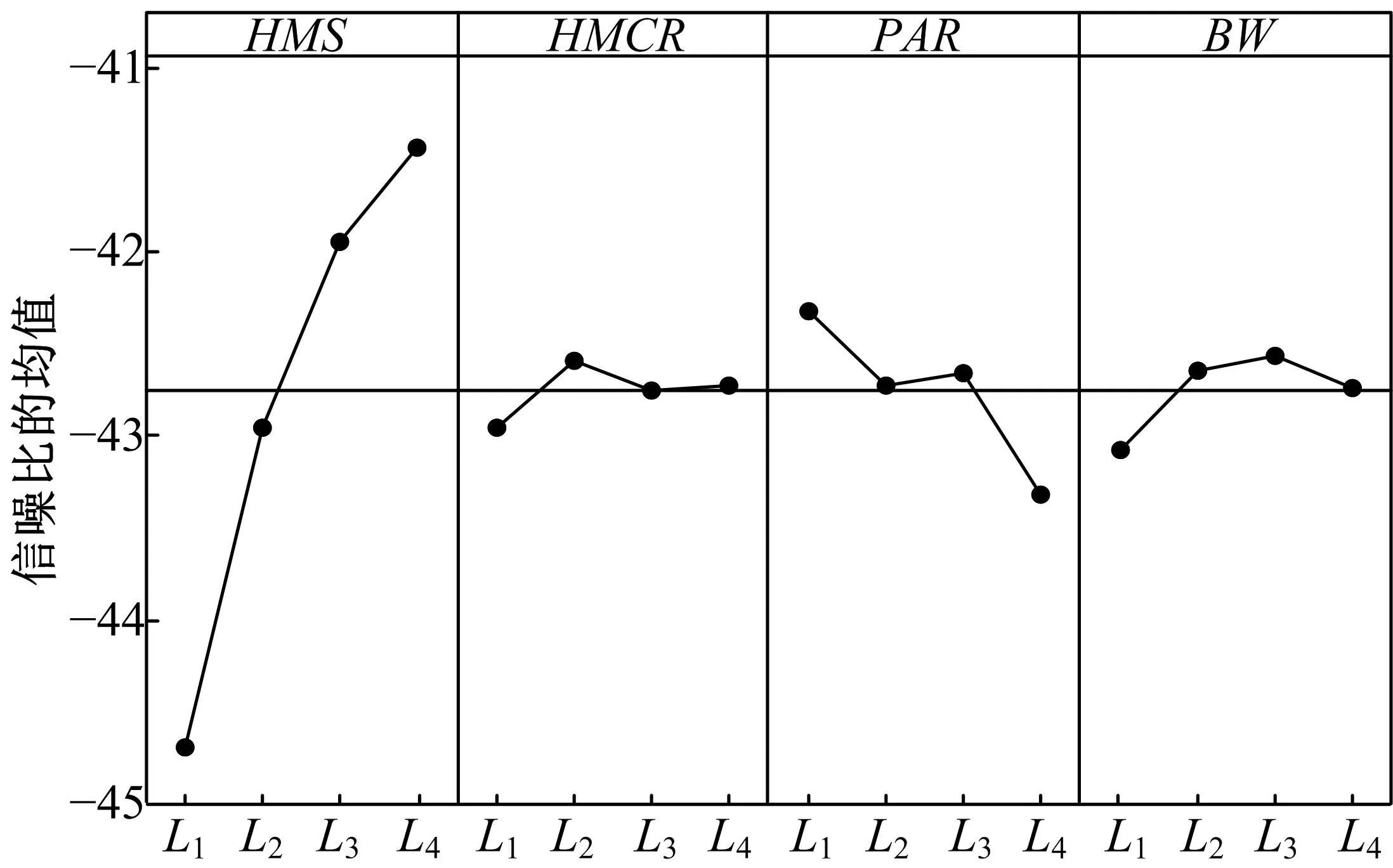
图2 HS参数的信噪比主效应图Fig.2 Main effects plot for SNR of HS factors

图3 IHS参数的信噪比主效应图Fig.3 Main effects plot for SNR of IHS factors
根据图2可知,HS算法的4种参数中,HMS对信噪比的影响最大,PAR的影响次之,然后分别是BW和HMCR。根据图2选取参数HMS为20,HMCR为0.9,PAR为0.2,BW为0.7。
根据图3可知,IHS算法的6种参数中,HMS对信噪比的影响最大;BWmin和BWmax的影响分别次之;然后是PARmax和PARmin;最后是HMCR。根据图3选取参数HMS为20;BWmin和BWmax分别为0.05和0.9;PARmax和PARmin分别为0.8和0.05;HMCR为0.99。
3 实例结果对比分析
本文采用文献[1]中的20个测试组数据。利用Matlab编程实现应用改进的和声搜索算法求解越库系统数学模型。20个测试组用IHS算法、HS算法和TS算法各计算10次,分别得到每组数据的试验最优解、试验最差解和试验平均解。应用枚举法求解20组数据最优解与最差解。如表3所示,根据枚举法对比TS算法、HS算法和IHS算法,3种算法的试验最优解为最优解的数量分别为12、17、19;试验最差解的均值分别为304.1、312.7和409.4,其中IHS算法的试验最差解整体小于HS算法和TS算法的试验最差解;试验总平均值分别为310.065、277.915和273.385,其中IHS算法的试验总平均值整体小于HS算法和TS算法的试验总平均值。
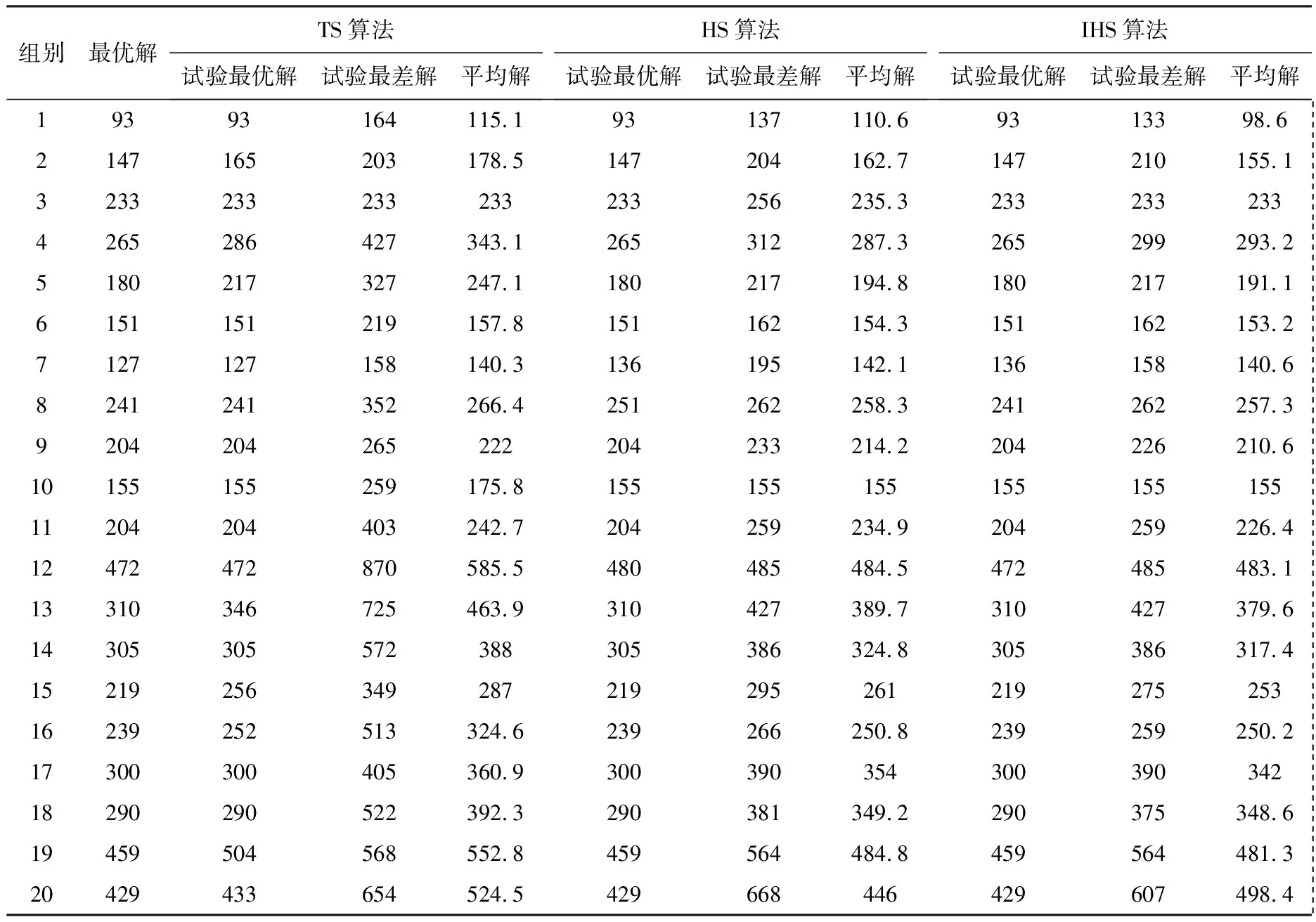
表3 算法的试验解比较Table 3 Comparison of experimental solutions
4 结束语
本文介绍了一种新颖的配送方式——越库作业,研究了只有一个入库门和一个出库门且带有暂存区的越库中心的作业车辆调度问题。从越库作业的总完工时间出发,以运作时间最小化为目标,建立了越库车辆排序问题的数学模型。为了减小计算中延迟时间的影响,将总运作时间的求解转化为计算临时库存中存储的物品数量。采用改进的和声搜索算法求解问题的近似最优解,与基本和声搜索算法和禁忌搜索算法进行比较,结果表明:改进的和声搜索算法在最优解数量与解整体优越性方面均优于基本和声搜索和禁忌搜索算法。
参考文献:
[1] Yu W,Egbelu P J. Scheduling of inbound and outbound trucks in cross docking systems with temporary storage[J]. European Journal of Operational Research,2008,184(1):377-396.
[2] Yu W. Truck scheduling for cross docking systems with multiple receiving and shipping docks[J]. International Journal of Shipping and Transport Logistics,2015,7(2):174-196.
[3] Madani-Isfahani M, Tavakkoli-Moghaddam R, Naderi B. Multiple cross-docks scheduling using two meta-heuristic algorithms[J]. Computers & Industrial Engineering,2014,74:129-138.
[4] Mohtashami A. Scheduling trucks in cross docking systems with temporary storage and repetitive pattern for shipping trucks[J]. Applied Soft Computing,2015,36(C):468-486.
[5] Arabani A R B, Ghomi S M T F, Zandieh M. Meta-heuristics implementation for scheduling of trucks in a cross-docking system with temporary storage[J]. Expert Systems with Applications,2011,38(3):1964-1979.
[6] Soltani R, Sadjadi S J. Scheduling trucks in cross-docking systems: a robust meta-heuristics approach[J]. Transportation Research Part E: Logistics and Transportation Review,2010,46(5):650-666.
[7] Assadi M T, Bagheri M. Scheduling trucks in a multiple-door cross docking system with unequal ready times[J]. European Journal of Industrial Engineering,2016,10(1):103-125.
[8] 缪朝炜,苏瑞泽,张杰. 越库配送车辆调度问题的自适应遗传算法研究[J]. 管理工程学报,2016,30(4):166-172.
Miao Zhao-wei,Su Rui-ze,Zhang Jie. An adaptive genetic algorithm for the truck scheduling problem in the crossdock distribution center[J]. Journal of Industrial Engineering and Engineering Management,2016,30(4):166-172.
[9] Geem Z H,Kim J H,Loganathan G V. A new heuristic optimization algorithm: harmony search[J]. Simulation,2001,76(2):60-68.
[10] Mahdavi M, Fesanghary M, Damangir E. An improved harmony search algorithm for solving optimization problems[J]. Applied Mathematics and Computation,2007,188(2):1567-1579.
[11] Valaei M R, Behnamian J. Allocation and sequencing in 1-out-of-N heterogeneous cold-standby systems: multi-objective harmony search with dynamic parameters tuning[J]. Reliability Engineering & System Safety,2016,157:78-86.
