将军饮马问题与中考题
2018-06-01刘永中
文 /刘永中
传说亚历山大城有一位精通数学和物理的学者,名叫海伦.一天,一位罗马将军专程去拜访海伦,向他请教一个百思不得其解的问题:将军每天骑马从城堡A出发,到城堡B,途中马要到小溪边饮水一次.问怎样走路程最短?
这就是广为流传的将军饮马问题.海伦略作思考,利用作对称点的方法解决了这个问题.
我们把将军饮马问题抽象成一个几何模型:条件:如图1,A,B是直线同旁的两个定点.
问题:在直线l上确定一点P,使PA+PB的值最小.
方法:作点A关于直线l的对称点A′,连接A′B,交l于点P,则PA+PB=A′B,PA+PB的最小值为A′B(证明略).
若能熟练利用将军饮马模型,则能轻松解决一些路程最短问题.

图1
一、四边形中的最短距离
例 1 如图2,菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是______.
解:如图2,连接DE交AC于P,连接BD,BP,
由菱形的对角线互相垂直平分,可得B,D关于AC对称,
则PD=PB,
∴PE+PB=PE+PD=DE,
即DE就是PE+PB的最小值.
∵∠BAD=60°,AD=AB,∴△ABD是等边三角形,
∵AE=BE,∴DE⊥AB.
在Rt△ADE中
故PE+PB的最小值为
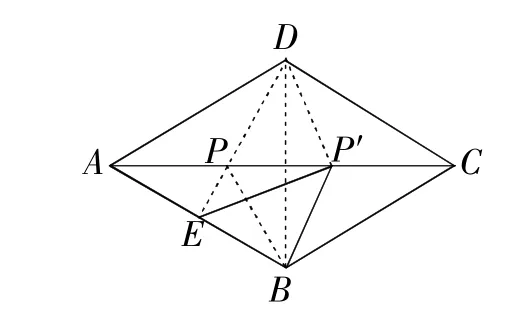
图2
二、一次函数中的最短距离
例3矩形OABC在平面直角坐标系中的位置如图3所示,点B的坐标为(3,4),D是OA的中点,点E在AB上,当△CDE的周长最小时,点E的坐标为( )

解:如图3,作点D关于直线AB的对称点H,连接CH,交AB于E,此时△CDE的周长最小.
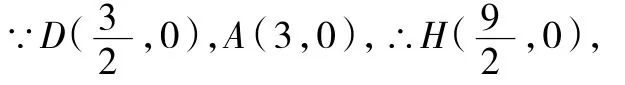
又∵C(0,4),∴直线
∴当x=3时,∴点E的坐标
选B.
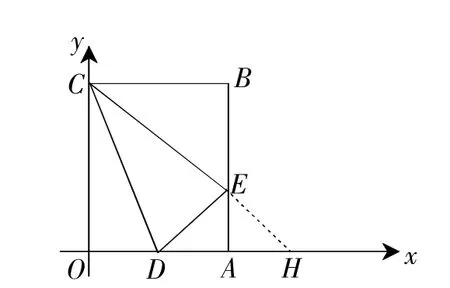
图3
三、二次函数中的最短距离
例4如图4,已知抛物线y=-x2+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0).
(1)求m的值及抛物线的顶点坐标;
(2)点P是抛物线的对称轴上的一个动点,当PA+PC最小时,求点P的坐标.
解:(1)将B(3,0)代入y=-x2+mx+3得m=2,
y=-x2+2x+3=-(x-1)2+4,所以顶点坐标为(1,4).
(2)如图4,点A的对称点是点B,连接CB,交对称轴l于点P,连接AP,此时PA+PC最小.
∵y=-(x-1)2+4,∴对称轴为x=1,C点坐标为(0,3).
设直线BC为y=kx+b(k≠0),把(3,0),(0,3)代入得

∴y=-x+3,
当x=1时,y=-1+3=2.
当PA+PC的值最小时,点P的坐标为(1,2).

图4
