尺规作图题的归类解析
2018-06-01朱广科
文 /朱广科
纵观近几年的中考作图题,已不局限于对基本作图技能的考查,取而代之的是设计新颖、富有创意的作图题.现把各种题型归类如下,供你复习时参考.
一、基本作图型
例1 如图1,A,B,C为某公园的三个景点,景点A和景点B之间有一条笔直的小路,现要在小路上建一个凉亭P,使景点B、景点C到凉亭P的距离之和等于景点B到景点A的距离,请用直尺和圆规在所给的图中作出点P.(不写作法和证明,只保留作图痕迹)
解:如图1,连接AC,作线段AC的垂直平分线MN,直线MN交AB于P.
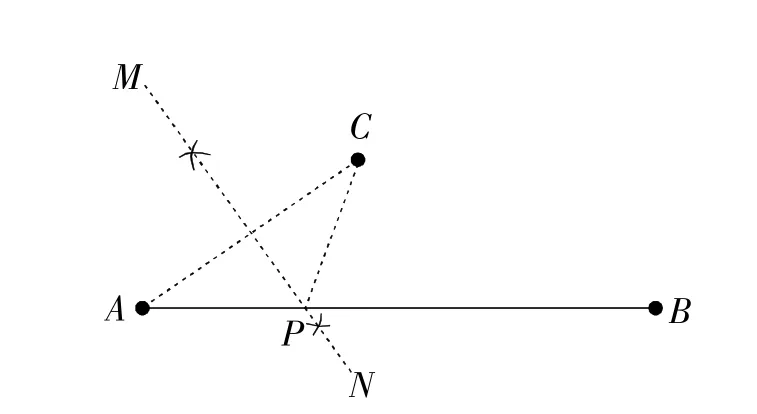
图1
点P即为所求的点.
点评:尺规作图是指用无刻度的直尺和圆规来作图,通常称为基本作图.解尺规作图题时,要明确直尺和圆规的功能.理解图形的本质特征,确定作图顺序是解题的关键,一定要保留作图痕迹.
二、图形剪拼型
例2七巧板是我国祖先的一项卓越创造.下列四幅图中有三幅是小明用如图2所示的七巧板拼成的,则不是小明拼成的那幅图是( )
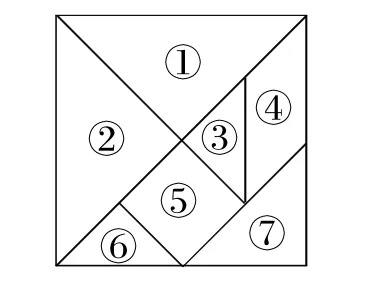
图2
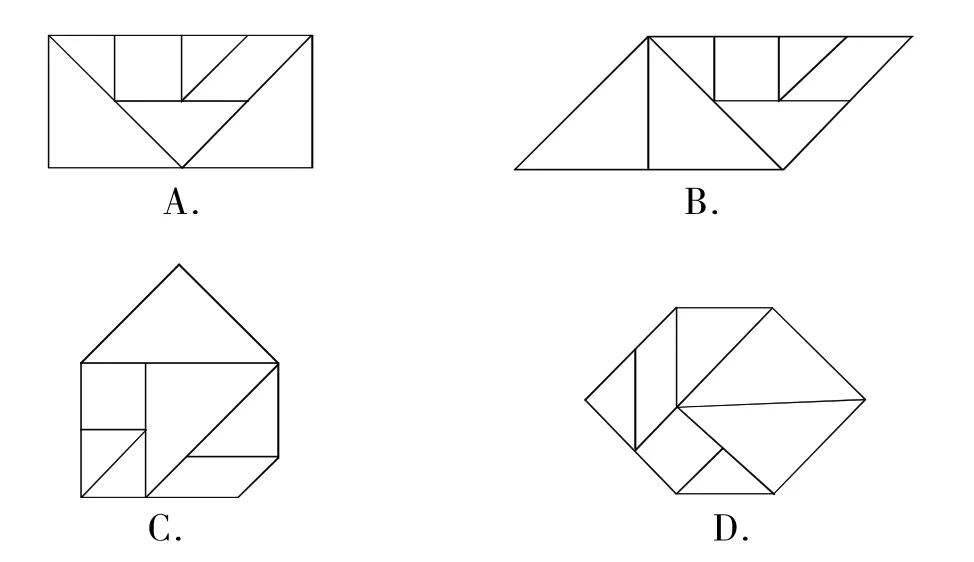
解:根据勾股定理,可判断边长之间的关系,不能构成C图案,能构成A,B,D图案.
选C.
点评:解答剪拼问题需要逻辑推理,要多方位、多角度、多层次地探索,观察拼接前后的图形,根据它们的边、角、面积之间关系确定正确选项.
三、图形变换型
例3在图3和图4中,4×4网格图都是由16个相同小正方形组成,每个网格图中有4个小正方形已涂上阴影,请在空白小正方形中,按下列要求涂上阴影.
(1)在图3中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个中心对称图形;
(2)在图4中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个轴对称图形,但不是中心对称图形.
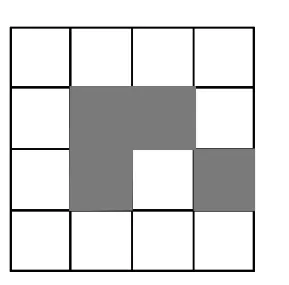
图4
解:(1)选取2个小正方形涂上阴影(新涂的阴影用灰色表示),使6个阴影正方形成中心对称图形,如图5所示.
(2)选取2个小正方形涂上阴影(新涂的阴影用灰色表示),使6个阴影小正方形成轴对称图形,但不是中心对称图形,如图6所示.
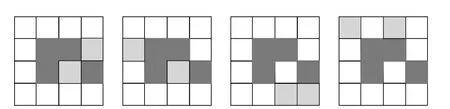
图5
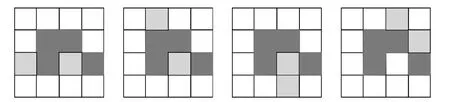
图6
点评:图形变换主要包括图形的平移、翻折、旋转等几种情况.解题的关键是观察图形并挖掘其中的变换条件,根据变换的性质确定图形的位置.
四、利用网格的特征作图
例4图7、图8、图9都是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点称为格点.线段AB的端点在格点上.
(1)在图7、图8中,以AB为边各画一个等腰三角形,且第三个顶点在格点上(所画图形不全等);
(2)在图9中,以AB为边画一个平行四边形,且另外两个顶点在格点上.
解:(1)根据等腰三角形的定义作图,以AB为底,△ABC为所求,如图7,以AB为腰,△ABD为所求,如图8.
(2)根据平行四边形的判定定理作图,如图9所示,▱ABCD即为所求.
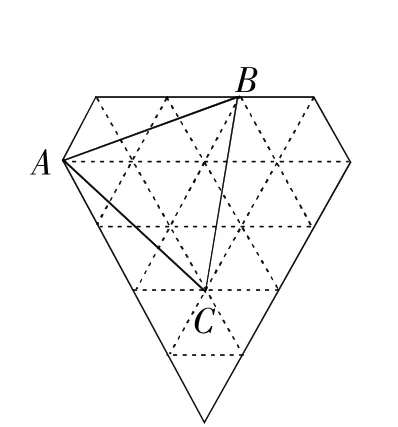
图7
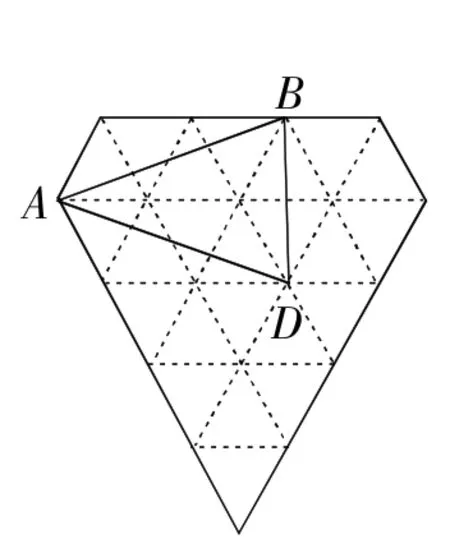
图8

图9
点评:以三角形网格为背景的作图题,不需要繁杂的计算和证明,凭借格点的特征,复杂的位置问题变得简单而生动.利用网格线平行的结构特征,结合等腰三角形、平行四边形的性质等,就能准确找出对应点的位置.
五、开放探究型
例5在平面直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的三角形为整点三角形.如图10,已知整点A(2,3),B(4,4),请在网格区域(含边界)按要求画整点三角形.
(1)在图10中画一个△PAB,使点P的横、纵坐标之和等于点A的横坐标;
(2)在图11中画一个△PAB,使点P,B横坐标的平方和等于它们纵坐标和的4倍.
解:(1)设P(x,y),由题意x+y=2,
∴ P(1,1)或(2,0)或(0,2),但(0,2)不构成三角形,舍去,
△PAB,△P′AB符合题意,如图10所示.
(2)设P(x,y),由题意得x2+42=4(4+y),x=2,y=1,符合题意,可得整点(2,1),△PAB符合题意,如图11所示.
点评:分类讨论是解题的关键.分类时,要认真思考,做到不重复不遗漏.
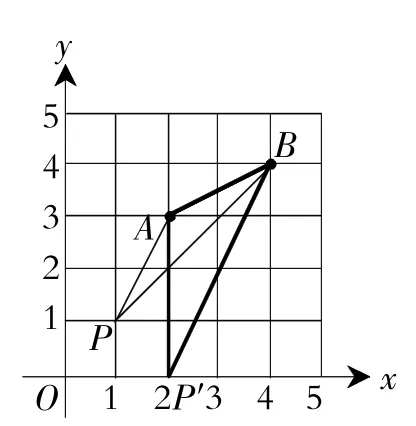
图10
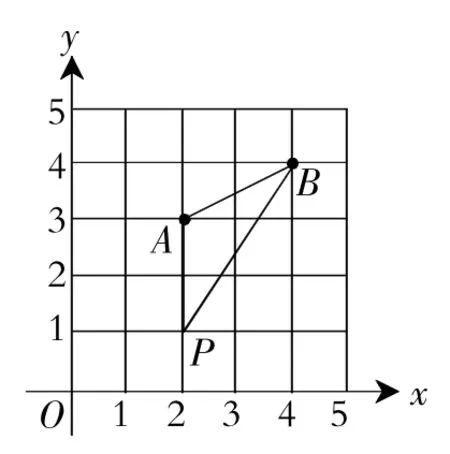
图11
六、阅读理解型
例6直角在初中几何学习中无处不在.
如图12,已知∠AOB,请仿照小丽的方式,再用两种不同的方法判断∠AOB是否为直角(仅限用直尺和圆规).
小丽的方法:如图13,在OA,OB上分别取点C,D,以C为圆心,CD长为半径画弧,交OB的反向延长线于点E,若OE=OD,则∠AOB=90°.
解:方法1:如图14,在OA,OB上分别截 取 OC=4,OD=3, 若 CD=5,则∠AOB=90°.
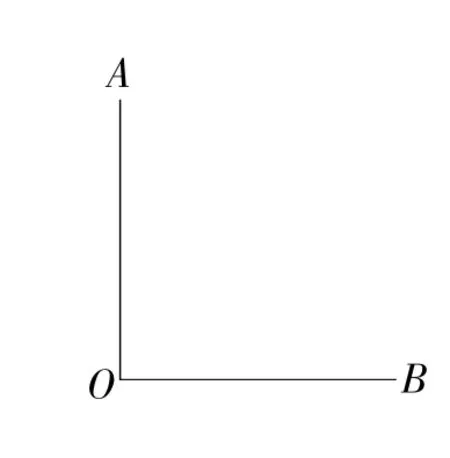
图12
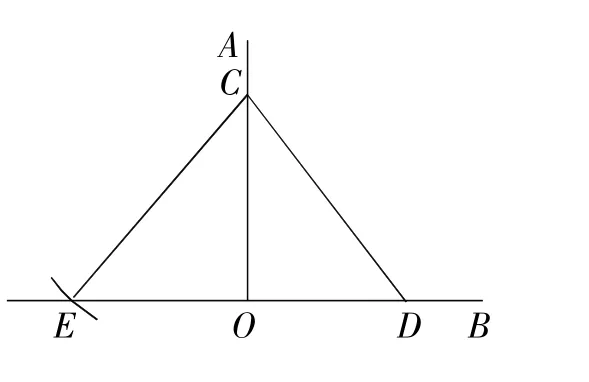
图13
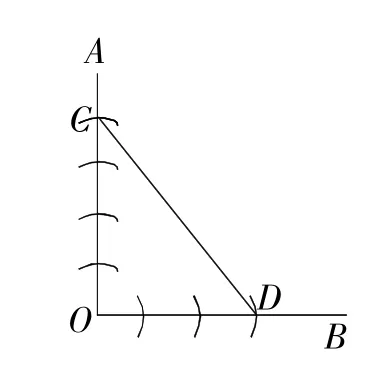
图14

图15
方法2:如图15,在OA,OB上分别取点C,D,以CD为直径画圆.若点O在圆上,则∠AOB=90°.
