影响少数民族高校计算机程序设计成绩的客观因素分析

王晓丹，王 正，怀丽波

（延边大学 计算机科学与技术专业，吉林 延吉 133002）

0 引 言

计算机程序设计课程不仅是培养学生编程能力的重要课程，也是养成学生计算思维的重要手段，一直被广泛关注。近年来，有关计算机程序设计课程的教学研究成果甚多，有基于教学模式[1-2]或提升学生主观意识方面的改革[3-4]，有基于特定人群的课程培养研究成果[5]，也有基于统计学检验方法在教学、科研领域的应用。但其中很多研究已暴露了明显不足：有些研究忽视了客观因素的现实存在及其影响，有些对客观因素缺乏科学的、深层的挖掘，甚至有检验方法的滥用、误用现象存在[6-7]。

1 数据有效性分析及预处理

本研究以少数民族地方性综合大学——延边大学为研究对象，该校农、医、文、史、经、法等18个学院将计算机程序设计设为公共必修课。本研究收集了2013—2017年共15 000多个观测，考生涵盖了30个省份和2个直辖市，共31个民族的学生，每届学生打乱专业随机分班，每届教师与专业班级不固定分配，既避免了数据抽样产生的误差问题，又排除了教师水平差异或班级学习氛围等主观因素对观测值的影响。

对数据分类或分组之前，数据的预处理是保证结论准确的必要环节。本研究首先通过数据审核，将缺考生、补考生及转专业学生的重复考试成绩等脏数据删除，以学号为唯一标识，保证仅取每名学生的第一次非零成绩为有效观测。通过对5届学生计算机程序设计成绩的数据清洗，共得到13 035个有效观测。程序设计的百分制成绩依照以下统计方法的需要将被分为优、良、中、及、差5个等级，或者及格、不及格2个等级。学生按照性别、考生类别、省份、民族4种方式分类后，可得到联合分布频数（见表1—表4）。

但联表中的数据是样本数据，它只是总体的代表，具有随机性，故需要用独立性检验的方法确认所得结论在多大程度上适用于总体。由于独立性检验有两条准则[8]：一是，如果只有两个单元，每个单元的期望频数必须是5或5以上；二是，对于两个以上的单元，必须满足20%以上的单元期望频数大于5。频数期望值公式如式1所示：

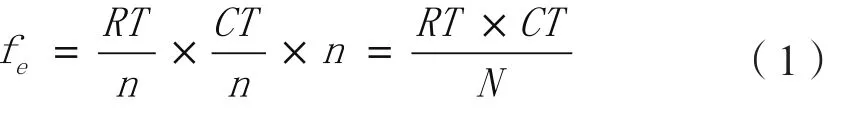
RT为给定单元所在行的合计；CT为给定单元所在列的合计；n为观测总数。为保证单元期望频数大于5，单元所在列的合计最小值可由式（2）得出：

表2 考生类别与成绩联合分布频数

表3 省份与成绩联合分布频数

表4 民族与成绩联合分布频数

因此，本研究在做民族与成绩的x2独立检验时，只保留人数最多的7个民族；相应的省份分类也保留了人数最多的7个，以保证相关系数比较分析结果的准确性。

2 分类数据的独立性检验

本研究采用独立性检验，通过列联表方式呈现及量化计算两个分类变量是否存在联系。仅以考生类别分类成绩与计算机程序设计成绩的相关性判定为例，说明x2检验的过程。

设H0:考生类别和计算机程序设计成绩之间是独立的（不存在依赖关系）；H1:考生类别和计算机程序设计成绩之间不独立（存在依赖关系）。通过频数期望计算公式（式1）及x2计算公式（式3），可列出考生类别与成绩统计量计算表（见表5）。

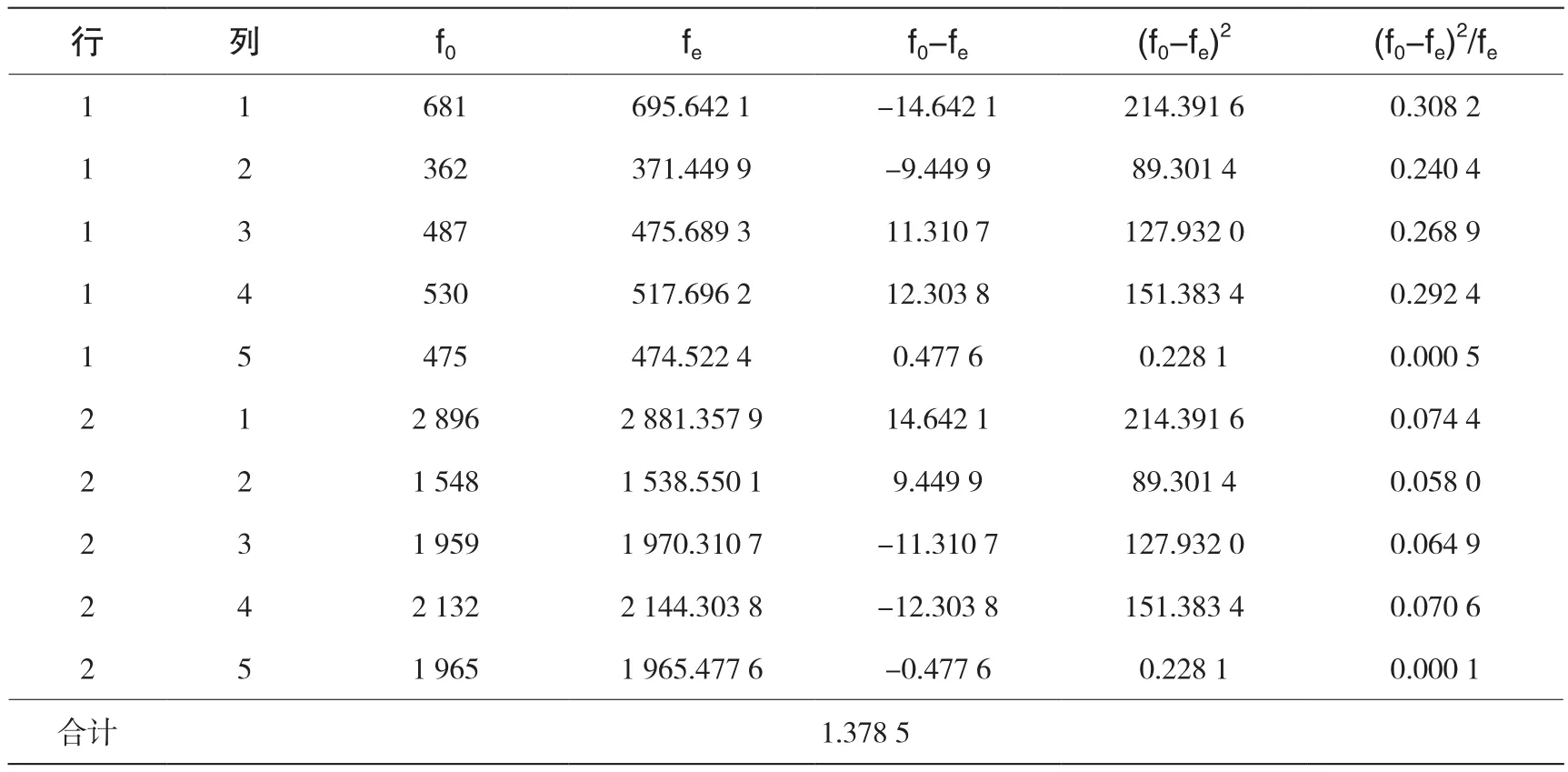
表5 统计量计算表

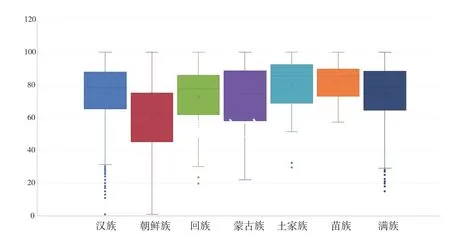
x2自由度=(R-1)(C-1)=4，为降低犯第二类错误的风险，即降低“零假设为假却被接受”的概率，可适当提高犯第一类错误的概率，故将a水平定的高一些[7]，可令a=0.1，查询《x2分布临界值表》可知：x20.1(4)=7.779。由于x2

2(4)，故接受H0，拒绝H1，即考生类别与计算机程序设计成绩之间不存在依赖关系，故我们不会对文理科类别继续进行相关系数的分析。

同样的方法可求得性别、省份、民族3个类别的x2值分别为 367.770，806.765，1 699.023。为降低犯第一类错误的风险，即降低“零假设为真却被错误拒绝”的概率[7]，可将a的值定得低一些。由《x2分布临界值表》显示，即使a取0.01，上述结果也远远大于中相应的x0.012(4)=13.277,x0.012(24)=42.980,x0.012(24)=42.980。

3 列联表的相关测量与因素的比较分析

在很多研究中发现，x2检验的前提条件和应用局限性往往被忽视了，为避免夸大该方法的功能，我们对结果进行了两方面的修正：一是要避免样本过大对检验结果的影响；二是通过不同分组的重复性试验，验证结论准确度。

3.1 相关系数检验

有研究表明当x2值达到显著程度而且样本含量又很大时， 需要参照Pearson 列联系数 C 值的大小， 如果C值也很大， 才可以拒绝零假设[6]。

公式（4）中x2由上一步的独立性检验得出，n为样本总数，因此C值的区间为0≤C<1。但只有相同行数和列数的联合分布频数表才可以比较。因此通过Pearson列联系数，首先可计算出省份、民族这两个类别的C相关系数值分别为0.2615、0.3410，从而确定了民族这一因素，与省份相比，与计算机程序设计课程成绩的相关程度更高。而且，省份与成绩的相关系数小于0.3，被认为是弱相关或不相关；民族因素结果所处范围是[0.3，0.5]，被认为是低度相关。

3.2 重分组检验

根据民族的箱线图（图1）显示：朝鲜族学生成绩的中位数（箱体中的横线）、上下四分位数（箱体上、下沿）以及最低成绩（最下方短线）均明显低于其他民族；而且有些民族的箱线尾部存在异常值，说明此民族仅有极个别学生的成绩异常低（一般认为超出箱体1.5倍距离的值为异常值），相反有25%的朝鲜族学生成绩较均匀地分布在（0，42）分之间，而非极偶然现象。

因此表6将学生分为朝鲜族和非朝鲜族两组，使其与性别分类的频数表（表1）行列数相等。再分别计算x2值，通过φ相关系数继续深入比较性别因素与民族因素对于成绩的影响程度。由计算得到性别与成绩的φ相关系数为0.18,而是否为朝鲜族的分类与成绩的φ相关系数为0.31。

综合两种检验方法，我们得出相同的检验结果：少数民族地区高校范围内，民族因素对计算机程序设计成绩影响最为显著；而且延边地区高校中朝鲜族学生的程序设计成绩明显低于其他民族学生的成绩。

图1 各民族学生成绩的图形比较

表6 民族与成绩的联合分布频数

4 实验结果分析

对以上实验过程继续深入分析，可得出以下几点结论：

（1）本研究选取的各个客观因素是教学过程及相关研究中涉及的，被认为会影响计算机程序设计成绩的几项因素。但统计结果表明，仅有民族这一因素与计算机程序设计成绩低度相关，省份与性别呈现弱相关或不相关性。由此可见：一是结论符合主观因素起决定作用的矛盾论观点；二是不排除其他客观因素对成绩的影响。

（2）本研究和同类研究相比，样本量较大，一方面最大限度地减小了随机抽样误差，但另一方面有可能引起x2值过大，因此验证零假设成立的准确性更高，即可以确定考生类别与计算机程序设计成绩之间不存在依赖关系。进而说明部分高校取消该课程的文、理科区别教育是明智之举。教师在教学过程中应充分相信文科生可以掌握该难度的程序设计，文科学生也应有信心掌握好该课程。

（3）研究中发现来自吉林省的学生成绩在省份分类中处于最低，有可能因为吉林省有42.3%的考生是朝鲜族，朝鲜族学生中85.7%来自吉林省，这种样本可能影响吉林省考生成绩的相关分析结论。但是研究中的样本虽不能保证各客观因素之间的影响完全分离，但实验数据在很大程度上能够体现民族、省份、性别因素的客观存在性。

（4）7个民族与7个省份之间的比较，是否为朝鲜族与性别之间的比较分析结果同时显示：少数民族地区的民族因素对计算机程序课程成绩的客观影响最为显著，尤其突出暴露了朝鲜族学生成绩落后的严重性，这也与教学过程中多数人的体验相吻合。笔者分析认为这与朝鲜族学生的自身特点及毕业去向有关。

第一，朝鲜族学校一直采用全朝鲜语授课，学习资料及高考试卷全部是朝文，因此朝鲜族学生对汉语课堂难免有不适应的情况；还有部分学生是日语考生，面对全英文的程序表现出了陌生感或是排斥感。第二，延边大学的学生会与社团中的多数主力，由谦恭有礼、能歌善舞的朝鲜族学生担任，丰富的活动练就了他们的综合素质，但也分散了很多学习精力，从而对成绩造成负面影响。第三，朝鲜语和韩国语的相通，使朝鲜族学生在韩企就业、赴韩留学时具有得天独厚的优势，也就使其在学习过程中感受到的压力明显小于其他民族的学生。

5 结 语

我们以较大的样本量、严谨的实验过程得出，影响计算机程序设计课程成绩的客观因素包括：民族、省份和性别，而考生类别与该课程成绩不相关。这一理论成果将为区别教育、辅助教学及其他教学方法的研究提供最可靠的理论依据，可作为该领域未来相关工作的基础。其中朝鲜族学生所代表的少数民族地区高校中，民族因素对成绩的客观影响最为显著，已由统计学方法多角度、科学地证实，值得后续研究更加深入地剖析其成因与机制。

[1] 钟玉峰, 运海红, 葛冬梅. 高校VB程序设计课程教学改革研究[J].黑龙江教育（高教研究与评估）,2013(5): 26-2.

[2] 李媛媛, 李艳辉, 沙继东. 高职自主学习型课堂教学模式的构建与实施——以程序设计课为例[J]. 中国成人教育, 2014(10):112-113.

[3] 康桂珍. 程序设计课程教学探析[J].中国教育信息化, 2012(19): 61-63.

[4] 田希山. 民族预科“程序设计语言”课教学探讨[J]. 宁夏大学学报, 2004(5): 6-8.

[5] 贾力, 王良, 杨智, 等. 文科学生程序设计课程的教学探讨[J].云南财贸学院学报, 2000(4): 93-96.

[6] 郑兵云. 非参数x2检验的两个局限性问题[J]. 统计教育, 2007(6): 8-9.

[7] 鲍贵, 席雁. 统计显著性检验: 问题与思考[J]. 南京工程学院学报（社会科学版）2010, 4(10): 27-32.

[8] 贾俊平, 何晓群, 金勇进. 统计学[M]. 6版. 北京: 中国人民大学出版社, 2015: 216-395.