基于机器视觉的草莓自动分级方法研究

杨 涛YANG Tao 张云伟 - 苟 爽

(昆明理工大学信息工程与自动化学院，云南 昆明 650500)

草莓的分级是其产后处理的一个关键环节[1]。当前中国草莓分级仍以人工为主，分级效率低、标准因人而异缺乏客观性、容易造成果肉机械损伤等缺点[2]。为解决这些问题，国内外的研究者展开了很多的研究。曹其新等[3]利用图像信息技术与神经网络技术开发了根据草莓外形分级的自动分拣系统；Nagata M等[4]研究了在OHTA色度空间下草莓的自动分离与分级方法；VOI等[5]将RGB模型转化为HIS模型，将新鲜断层的累积H分布图分为6个成熟度等级；Nakano等[6]开发了苹果图像采集系统，采用神经网络的方法将苹果分为5个等级；Masatera等[7]通过形状和大小特征来进行草莓分级；Bato等[8]通过图像处理实现草莓取向和形状确定；冯斌等[9]的水果分级系统提供了2种快速检测图像边缘的方法，利用果实表面色调分布在线分级。研究者大多都是从草莓颜色或者外形单一角度去研究机器视觉环境下的草莓自动分选方法，没有全面考虑各因素对草莓品质的影响。

本研究拟从成熟度、质量、形状三方面综合评估草莓品质，经过加权运算计算出一个综合评级分数，以达到快速、准确实现草莓自动分级处理的要求。

1 基于HSV颜色模型的草莓成熟度判别

1.1 利用HSV模型分析草莓颜色分布

HSV颜色模式是一种主观彩色模型，采用色调、饱和度和纯度描述颜色的3种属性[10-11]。这种格式反映了人类观察色彩的方式，避免了环境中光线强弱对物体表面颜色的影响。在HSV模式中H是反映色彩本质特性的参数，表示颜色的种类。成熟草莓果肉呈现为红色和橙色2种颜色，成熟度越高红色所占比例越高，果肉颜色的H参数直方图呈窄幅集中分布，红色和橙色各自形成2个小高峰，见图1。因此，采用H分量就可以实现对草莓红色和橙色区域的分类。

试验中提取样本草莓HSV模型的H参数，统计每个样本草莓图像H参数区域分布的概率数据。成熟草莓果肉表面绝大部分呈红色，少数区域颜色为橙黄色。经过多次试验，针对安娜品种草莓，选定将HSV模型中H参数的量程18等分，每个区域内的颜色非常接近，见图2。该品种草莓H参数数值都在第1、2、3区域和第4区域前半部分，表征成熟度高的红色对应H参数高度集中0°～20°和350°～360°对应区域。表征不完全成熟的橙色和橙黄色对应H参数在20°～60°区域内，见图3。

1.2 草莓成熟度判别方法

用151颗安娜品种草莓作为试验样本进行草莓成熟度等级判别研究。首先采用人工分类方法从151个样品草莓中选出成熟度不达标的劣次品。为尽量排除个人分类对草莓分级类别造成的主观性差别，试验中邀请10人分别独立完成筛选工作。实施方法：① 将151个草莓随机从1～151顺次编号；② 每位参评人员独立地从成熟度的角度筛选出成熟度不达标的草莓，并记录其对应的编号。分级评判结果见表1。

为避免草莓果实外表的黄色斑点对成熟度分析造成不确定误差，利用计算机图像技术对151个样本草莓进行图像分割、滤波去噪处理，将草莓果实表面黄色斑点从图像中分离舍去。提取每张草莓图像对应HSV模型中表征颜色的H参数，按照式(1)统计每个草莓成熟度达标的红色区域像素数量百分比K，151个样本草莓的K值统计结果见图4。结合表1和图4可知：人工分级选出的三等品草莓对应K<0.88，统计表1中出现频率>6次的15颗草莓其对应K<0.86。因此试验中选取K=0.86作为成熟度阈值。当计算出待测样本草莓K<0.86时，表示该草莓成熟度不达标，属于劣次品，不参与后续的检测评级；当待测草莓K≥0.86时，该草莓已成熟，进入下一检测流程。

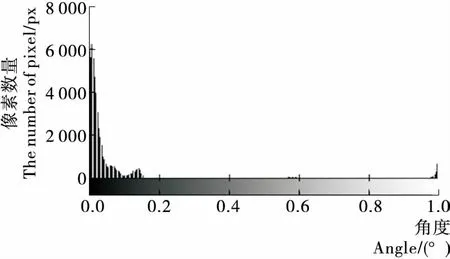
图1 草莓图像H参数直方图Figure 1 H parameter histogram of Strawberry image

图2 HSV颜色模型图Figure 2 HSV color model

图3 草莓颜色区域分布图Figure 3 Strawberry color area distribution

K=n1/n2，

(1)

式中：

K——草莓红色区域像素数量占比，%；

n1——草莓红色区域像素数量，px；

n2——草莓像素总量，px。

2 草莓质量测算与标准确立

成熟度之外，质量大小是评判草莓等级的另一个特征因素。因此，探究草莓质量与图像之间的内在关系，利用这种关系通过图像信息分析间接完成草莓质量测定是研究的另一个重点内容。同一品种草莓的果形对应1种或2种几何形状，单个草莓之间形状相似度较高。经过试验分析验证，同品种草莓的质量与果肉面积的关系可以用线性函数近似描述，由此，已知图像投影面积在函数关系成立的定义域内，即可间接确定草莓质量。

表1 劣次品草莓筛选统计表Table 1 Selected samples of Inferior strawberry

图4 样本草莓K值统计图Figure 4 Sample strawberry K value chart

试验中选用安娜品种草莓作为样本，该品种草莓果形为圆锥形或长圆锥形，最大质量能达到40 g。参照NY/T 1789—2009标准，对该品种草莓的质量分级数据见表2。

表2 品种草莓质量分级数据Table 2 Variety of strawberry mass grading data

标定：在采集草莓图像时，旁边放置一个2 cm×4 cm的红色标定图片(见图5)，求出草莓的像素面积和红色标定图片像素面积，根据红色标定图片实际面积得出草莓投影面积。

图5 标定图Figure 5 Calibration chart

通过试验测定样本草莓的质量与投影面积，拟合草莓质量与投影面积的函数关系。用精确度为0.01 g的天平测量余下136个样本草莓实际质量；利用计算机图像处理技术计算、统计出每个草莓的投影面积；以试验样本的质量数据作横坐标(从小到大升序排列)，与其一一对应的样本投影面积作函数值，画出投影面积-质量关系图，见图6(a)。

当然，即便将“节约资源，保护生态环境”作为物权取得和行使的原则性规定，也不能理解为将环保利益优位于民事利益，而更应将“绿色原则”解读为搭建起了沟通经济利益和环保利益的价值关联和制度桥梁，为物权取得和行使限定了生态环保利益的界限。“这是民法在自己的制度弹性范围内，在权利本位的基础上对又一种社会利益——生态环境保护利益的兼顾。”［8］69简言之，“绿色原则”在“物权编”中应成为对物权取得和行使的价值限度。

由图6(a)可知：草莓质量介于13～28 g时，投影面积随质量的递增而呈线性增长；当质量>28 g或<13 g时，投影面积与质量的线性关系逐步变差。试验中，设定质量的一等品下限阈值为24 g，二等品范围对应[18，24] g，三等品下限阈值13 g。结合表2与图6作如下规定：草莓质量评级分范围为[7，10]分，质量>28 g的草莓对应质量评级分为10分，质量<13 g的草莓直接分级为次等品，不再参与后续评级检测。

试验样本中，质量介于13～28 g的草莓共计101个，统计该区间草莓对应的投影面积与质量数据，见图6(b)。由统计数据拟合出投影面积-质量函数关系y=f(x)为：

y=0.493x+2.031x∈[13,28]。

(2)

求y的反函数，得到质量-投影面积函数关系式y=φ(x)为：

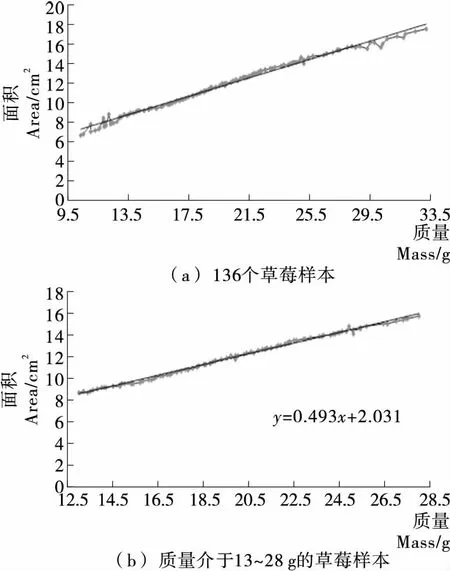
图6 投影面积-质量关系图Figure 6 Image area-mass relationship diagram

y=2.028x-4.12x∈[8.440,15.835]。

(3)

质量-投影面积函数φ(x)的值域为[13,28]，设定质量评分函数为φ(x)，草莓质量评分数函数的值域为[7,10]，则由φ(x)映射到φ(x)有如下变换：

(4)

φ(x)=0.405 6x+3.576x∈[8.440,15.835]。

(5)

3 基于K均值聚类分析的草莓形状分析原理

草莓外形特征是评判其品质的另一个决定因素。已知草莓品种的果形有圆锥形、长圆锥形、短圆锥形、楔形四类，不同品种的草莓之间果形各有差异，但相同品种的草莓果形相同，单个草莓之间形状相似度较高。

3.1 草莓形状特征提取

描述水果形状特征的方法有很多，常见的方法有均分直线法和半径序列法。均分法指利用数条相互垂直的水平和竖直线均分草莓，由这些直线描述形状。半径序列法即为从水果图像的重心引发出数条半径序列来描述水果的形状，见图7。将2种方法对比试验后发现，由于同一种草莓形状具有相似性与几何对称性，采用半径序列法计算草莓相似度与人工判断更接近。故本试验中选用半径序列法计算草莓形状特征参数。草莓重心o为极坐标系原点，l为草莓顶部端点。连结ol，并确定为极坐标系起始轴，沿正反2个方向平均每旋转18o从o点引出一条线段交于草莓边沿，得到ol1,ol2,…,ol9和ov1,ov2,…,ov9。用ol1,ol2,…,ol9和ov1,ov2,…,ov9分别除以ol作归一化处理消除草莓大小的影响，得到18个形状特征参数。

图7 草莓形状特征表示方法Figure 7 Expressive method of detected shape of strawberry

3.2 形状聚类与判别评级原理

以一定数量的草莓数据为样本，利用K均值聚类法完成草莓形状聚类[12]。K均值聚类法的具体过程为：① 从n个数据中随机选择K个对象作为初始聚类中心；② 利用布洛克距离(City Block Distance)计算剩余对象与聚类中心的相似度；③ 根据相似程度将每个对象分配给与其最相似的聚类，重新计算每个新聚类的聚类中心；④ 重复上述第二、第三步直到没有对象被重新分配给不同聚类为止。布洛克公式：

(6)

式中：

dij——相似度，%；

xiK——样本草莓i；

xjK——样本草莓j；

n——样本草莓总数。

判断评级具体指利用样本聚类信息，构造体现分类特点的关系数据矩阵，再利用关系矩阵判断待测样本的类别，并根据待测样本不同的类别归属给出相应的形状等级评分[13-15]。

本研究中，利用K聚类法和聚类距离判别法相结合建立草莓形状识别法。令ni1=l1/l，ni2=l2/l，…，ni9=l9/l，ni10=v1/l，ni11=v2/l，…，ni18=v18/l。(ni1,ni2,…,ni18)表示单个草莓形状特征参数。利用式(6)计算各样本草莓之间的相似度，根据相似度采用K均值聚类法对所有样本草莓聚类处理。从各类别中选取一定数量样本构造标准形状特征参数，计算待测草莓样本与各类标准形状样本参数的相似程度，以此判别待测样本的类别。

3.3 聚类试验步骤

试验样本为151个安娜品种草莓，利用半径序列法提取样本草莓形状特征参数，构造151×18的数据矩阵。

聚类时，分别将草莓分成三类、四类、五类，对比分类结果发现分成四类时，分类效果更接近人工分类处理。因此，采用基于Cityblock Distance原理与K均值聚类法对样本聚类处理。根据聚类分析得到的四类聚类重心，计算每组类别中各样本与聚类重心的距离。从每组类别中找出15个与聚类重心最接近的样本，组成4×15×18数据矩阵，该数据矩阵即为标准形状特征参数矩阵。

由表3可知，聚类分析将样本草莓大致分为长圆锥形、圆锥形、短圆锥形、近方形四类。

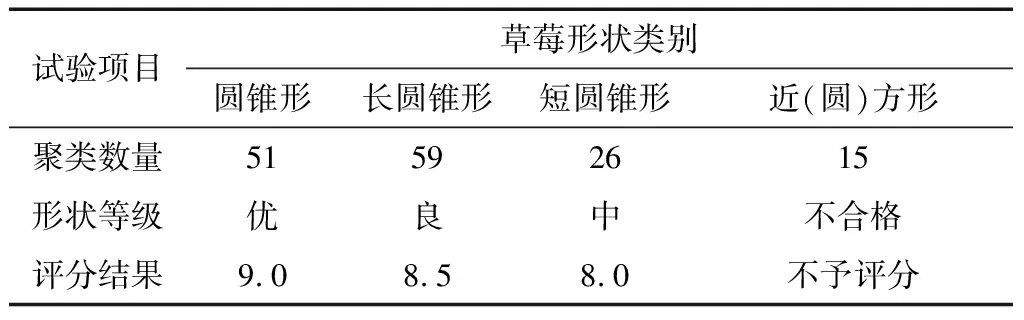
表3 草莓的K均值聚类及形状评分结果†Table 3 K-means clustering and shape score of strawberry

† 评分说明：安娜品种草莓以圆锥形和长圆锥形果型居多，短圆锥形相对较少。参考该品种标准果型对不同果形样本草莓给出相应形状评分。近方(圆)形果型属于不合格果形，该果形草莓分为劣次品，不参与等级划分的权值计算。

4 草莓自动分级工作流程

该分选系统分4个主要工作流程：第一步，检测草莓成熟度是否达标，不达标者视为劣次品，将其剔除且分级结束，达标者进入第二步流程；第二步，计算草莓图像面积，判断图像面积是否不小于最小阈值，不成立则视该草莓为劣次品，将其剔除且分级结束，成立则利用函数式(5)计算质量评分，并进入第三步流程；第三步，利用式(6)计算待测草莓形状特征参数与各类标准形状特征参数的相似度，剔除形状不合格的草莓；第四步，加权计算草莓质量评级分与形状评级分，给出草莓品质等级。工作流程图见图8。

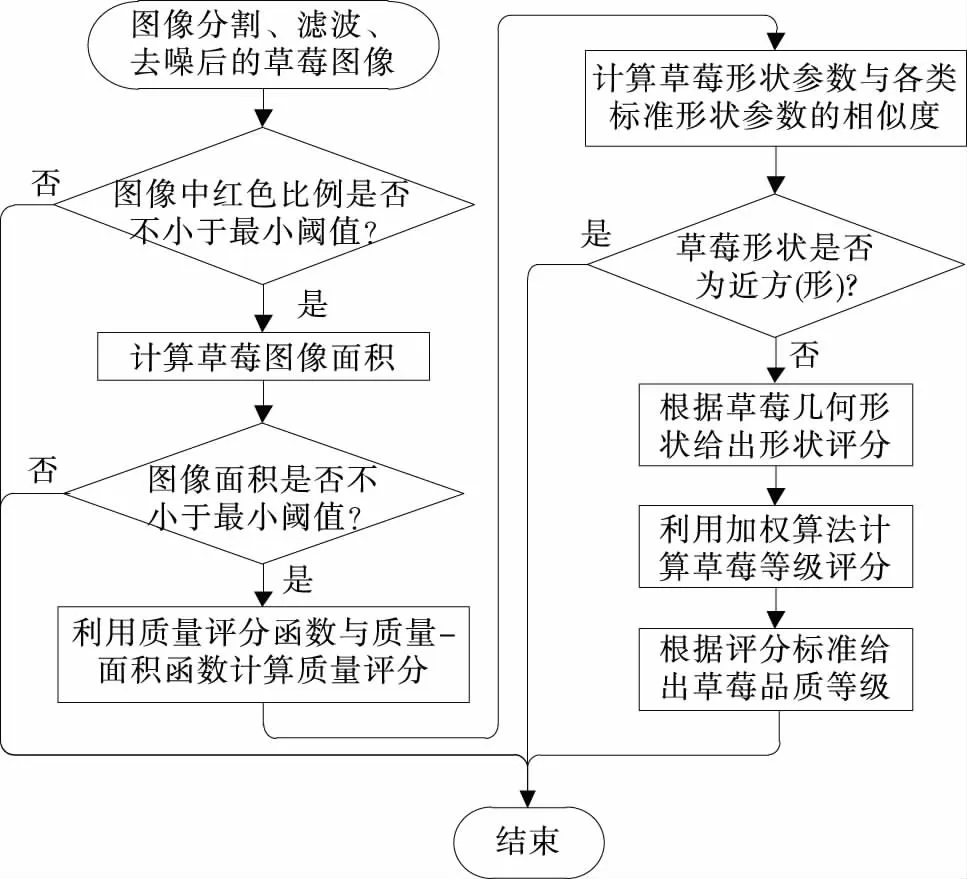
图8 自动分级工作流程图Figure 8 Automatic grading work flow chart

5 测试结果及分析

选取80幅新的草莓图像进行等级分类测试，设定草莓等级分为一等品、二等品、三等品与劣次品四类，分级测试的结果见表4。与人工分级结果对比，共有4个草莓出现分级结果不一致，主要原因是3个二等品草莓由于图像采集视觉原因造成质量评分误差，使其中2个被认定为一等品、1个被认定为三等品；有1个形状缺陷不明显的草莓没有被形状分级法识别出来，被分级为短圆锥形草莓类。

表4 草莓分级测试结果†Table 4 Strawberry grading results

† 测试耗时3.52 s。

6 结论

本研究在计算机图像信息基础上，从成熟度、质量大小和形状特征三方面分别对草莓进行相应评级处理，利用逻辑运算关系串联3个工作流程，建立了一套草莓自动分级系统。该分级系统分级速度快、不需要样本训练，避免了人工选择存在的主观偶然性。利用该系统对80个草莓进行分级测试试验，分级准确率达到90%以上(分类错误的草莓只出现在相邻等级，没有越级果)，共耗时3.52 s。该系统可以满足草莓实时分级需要。

[1] 乔勇进, 王海宏, 方强, 等. 草莓采后处理及贮藏保鲜的研究进展[J]. 上海农业学报, 2007, 23(1): 109-113.

[2] 刘禾, 汪懋华. 水果果形判别人工神经网络专家系统的研究[J]. 农业工程学报, 1996, 12(1): 172-176.

[3] 曹其新, 吕恬生, 永田雅辉, 等. 草莓拣选机器人的开发[J]. 上海交通大学学报, 1997, 7(7): 881-884.

[4] NAGATA M, KINOSHITA O, ASANO K, et al. Studies on automatic sorting system for strawberry(Part 1):Extraction of Geometric Feature Using Image Processing[J]. Journal of Jasm, 1996, 58: 57-63.

[5] VOI N. Tomato maturity evaluation using colour image analysis[J]. Transaction of the ASAE, 1995, 38(1): 171-176.

[6] NAKANO K. Application of neural networks to the colour grading of apples[J]. Computers and Electronics in Agriculture, 1997, 18(2): 105-116.

[7] MASATERA N, OSAMU K. Studies on automatic sorting system for strawberry(Part 3): Development of Sorting System Using Image Processing[J]. Journal of Japanese Society of Agriculture Machinery, 1997, 59(1): 43-48.

[8] BATO P M, NAGATA M, CAO Xin-qi. Study on the sorting system for strawberry using machine vision(Part2): Development of sorting system with direction and judgment functions for strawberry[J]. Journal of the Japanese Society of Agriculture, 2000, 62: 101-110.

[9] 冯斌, 汪懋华. 基于颜色分形的水果计算机视觉分级技术[J]. 农业工程学报, 2002, 18(2): 141-144.

[10] 钟小华, 曹玉华, 张永清, 等. 基于机器视觉技术的红枣全表面信息无损分拣系统研究与实现[J]. 食品与机械, 2017, 33(5): 114-118.

[11] 毕智健, 张若宇, 齐妍杰, 等. 基于机器视觉的番茄成熟度颜色判别[J]. 食品与机械, 2016, 32(12): 133-136.

[12] 徐黎明, 吕继东. 基于同态滤波和K均值聚类算法的杨梅图像分割[J]. 农业工程学报, 2015, 31(14): 202-208.

[13] 王辉, 毛文华, 刘刚, 等. 基于视觉组合的苹果作业机器人识别与定位[J]. 农业机械学报, 2012, 43(12): 165-170.

[14] 谢志勇, 张铁中, 赵金英. 基于Hough变换的成熟草莓识别技术[J]. 农业机械学报, 2007, 38(3): 106-109.

[15] XU Li-ming, ZHAO Yang-chao. Automated strawberry grading system based on image processing[J]. Computers & Electronics in Agriculture, 2010, 71(1): S32-S39.