计数原理拔高卷（A卷）答案与提示

一、选择题

1.B 2.C 3.C 4.D 5.B 6.C 7.B 8.D 9.D 10.A 11.C 12.D 13.D 14.B 15.C 16.C 17.C 18.B 19.D 20.C 21.A 22.A 23.C 24.C 25.C 26.B 27.C 28.D 29.C 30.B 31.C 32.A 33.B 34.A 35.C 36.C 37.B 38.C 39.A

二、填空题

40.8 41.455442.22 43.1260 44.12 45.90 46.19 47.24 48.12 49.22n-150.10 51.1.172 52.30 53.-5 54.-20 55.250056.5 57.1或-3

三、解答题

58.根据A球所在位置分三类:

①若A球放在3号盒子内,则B球只能放在4号盒子内,余下的3个盒子放球C,D,E,则不同的放法有3×2×1=6(种);

②若A球放在5号盒子内,则B球只能放在4号盒子内,余下的3个盒子放球C,D,E,则不同的放法有3×2×1=6(种);

③若A球放在4号盒子内,则B球可以放在2号,3号,5号盒子中的任何一个,余下的3个盒子放球C,D,E的不同放法有3×2×1=6(种),则不同的放法有3×6=18(种)。

综上,不同的放法共有6+6+18=30(种)。

59.(1)能被25整除的数有两类。后两位是50时,总的个数是=120;后两位是25时,先排首位有4种方法,其他四位有种方法,个数为4×=96。

能被25整除的数有120+96=216(个)。

(2)0,1,2,3,4,5,6构成无重复数字的七位数有6个,x,y,z分别表示个位、十位、百位上的数字,且满足x＜y＜z的数共

(3)先把4个偶数放在一起,有种排法,再把4个偶数看作1个元素与3个奇数组成4个元素进行排列,有种排法,总的排法有=576(种)。

由于此种排法会出现0在首位的现象,故从总的计数中减去0在首位的排法个数,0在首位时,3个偶数的排法有种,3个奇数排在个、十、百位也有种方法,故0在首位的排法有=36(种)。

所以偶数必须相邻的数有576-36=540(个)。

60.(1)每人都可以从这3个比赛项目中选报1项,各有3种不同选法,由分步乘法计数原理知,共有报名方法36=729(种)。

(2)每项限报1人,且每人至多参加1项,因此可由项目选人,第一个项目有6种选法,第二个项目有5种选法,第三个项目只有4种选法,由分步乘法计数原理知,共有不同的报名方法6×5×4=120(种)。

(3)由于每人参加的项目不限,因此每一个项目都可以从这6人中选出1人参赛,由分步乘法计数原理知,共有不同的报名方法63=216(种)。

61.(1)显然对应是一一对应的,即为a1找象有4种方法,a2找象有3种方法,a3找象有2种方法,a4找象有1种方法,所以不同的f共有4×3×2×1=24(个)。

(2)0无原象,1,2,3有无原象不限,所以为A中每一个元素找象时都有3种方法。所以不同的f共有34=81(个)。

(3)分为如下四类:

第一类,A中每一个元素都与1对应,有1种方法;

第二类,A中有2个元素对应1,一个元素对应2,另一个元素与0对应,有C24·C12=12(种)方法;

第三类,A中有2个元素对应2,另2个元素对应0,有=6(种)方法;

第四类,A中有一个元素对应1,一个元素对应3,另2个元素与0对应,有=12(种)方法。

所以不同的f共有1+12+6+12=31(个)。

62.(1)只需从其他18人中选3人即可,共有=816(种)选法。

(2)只需从其他18人中选5人即可,共有C518=8568(种)选法。

(4)由总数中减去5名都是内科医生和5名都是外科医生的选法种数,得C58)=14656(种)选法。

63.(1)由题意,得=256,即2n=256,解得n=8。

64.(1)因为,所以n2-21n+98=0,n=7或n=14。

当n=7时,展开式中二项式系数最大的项是T4和T5。

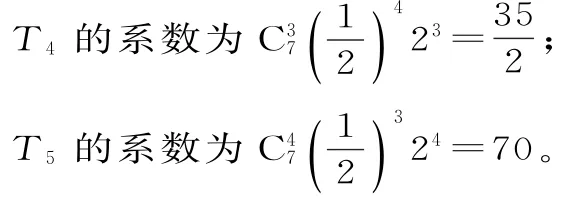
当n=14时,展开式中二项式系数最大的项是T8,因此,T8的系数为3432。

(2)因为=79,所以n2+n-156=0,n=12或n=-13(舍去)。

设Tk+1项的系数最大。

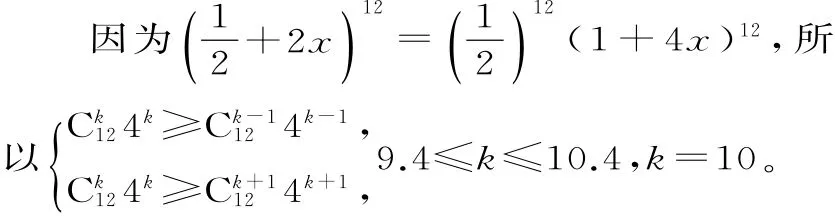
展开式中系数最大的项为T11。

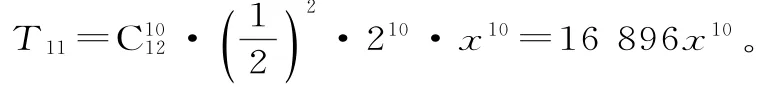
65.易求得展开式前三项的系数为1,

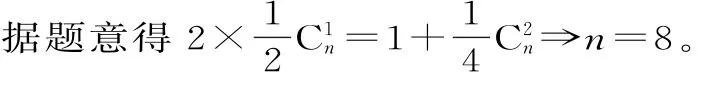
(1)设展开式中的有理项为Tk+1。

(4)|a0|+|a1|+|a2|+…+|a7|,即(1+2x)7展开式中各项的系数和,令x=1,故|a0|+|a1|+|a2|+…+|a7|=37=2187。