高考中常见的涂色问题
2018-05-31河南省平顶山市第一高级中学景路明
■河南省平顶山市第一高级中学 景路明
涂色问题是高考中比较常见的一类问题,这类问题新颖独特,具有一定的难度,能全面考查同学们的创新思维能力、分析问题与解决问题的能力。那么涂色问题主要有哪些呢?
一、平面区域的涂色问题
例1 如图1,用4种不同的颜色对图中5个区域涂色(4种颜色全部使用),要求每个区域涂一种颜色,相邻的区域不能涂相同的颜色,则不同的涂色种数有____。
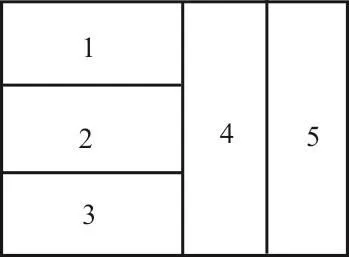
图1
分析:由于区域1,2,3与区域4相邻,由条件知宜采用分步处理方法,又相邻区域不同色,可按区域1和区域3是否同色分类求解。
解:按区域1与3是否同色分类:
(1)区域1与3同色,先涂区域1与3有4种方法,再涂区域2,4,5(还有3种颜色)有A33种方法,因此,区域1与3涂同色,共有4A33=24(种)方法;
(2)若区域1与3不同色,先涂区域1与3有A24种方法,第二步涂区域2有2种涂色方法,第三步涂区域4只有1种方法,第四步涂区域5有3种方法,此时,共有A24×2×1×3=72(种)方法。
故由分类加法计数原理可知,不同的涂色种数为24+72=96。
点评:解决涂色问题,一定要分清所给的颜色是否用完,并选择恰当的涂色顺序。切实选择好分类标准,分清楚哪些可以同色,哪些不能同色。
二、立体图形中的点涂色问题
例2 如图2,用4种不同颜色给图中的A,B,C,D,E,F6个点涂色,要求每个点涂一种颜色,且图中每条线段的2个端点涂不同颜色,则不同的涂色方法共有____种。
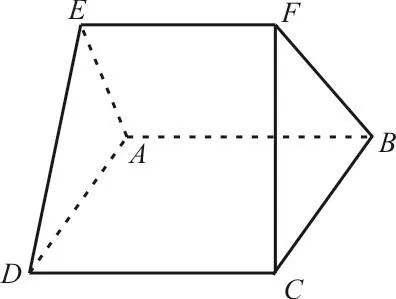
图2
分析:先分类,再分步,综合应用分类、分步计数原理加以解答。
解:先涂 A 、D、E三个点,共有4×3×2=24(种)涂法,然后再按B、C、F的顺序涂色,分为两类:一类是B与E或D同色,共有2×(2×1+1×2)=8(种)涂法;另一类是B与E或D不同色,共有1×(1×1+1×2)=3(种)涂法。所以不同的涂色方法共有24×(8+3)=264(种)。
点评:求解排列组合问题的思路:“排组分清,加乘明确;有序排列,无序组合;分类相加,分步相乘。”
三、立体图形中的面涂色问题
例3 如图3所示的几何体是由一个正三棱锥P-ABC与正三棱柱ABC-A1B1C1组合而成,现用3种不同颜色对这个几何体的表面染色(底面A1B1C1不涂色),要求相邻的面均不同色,则不同的染色方案共有____种。
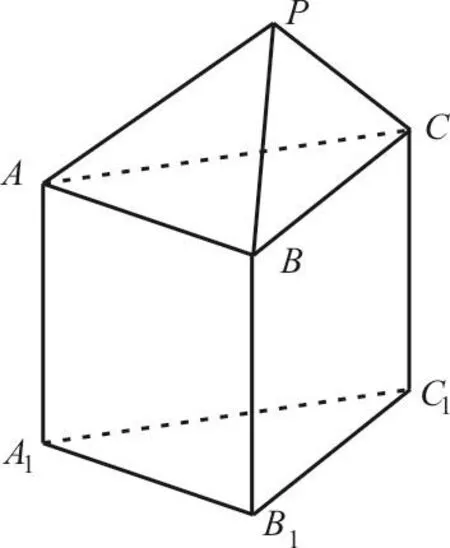
图3
分析:解答本题要注意底面A1B1C1不涂色这一条件,同时要分清是排列问题还是组合问题。
解:先涂三棱锥P-ABC的三个侧面,然后涂三棱柱的三个侧面,共有C13×C12×C11×C12=3×2×1×2=12(种)不同的涂法。
点评:解答排列组合问题,要仔细审题,判断是排列问题还是组合问题,要按元素的性质分类,按事件发生的过程进行分类;还要深入分析,注意分清是乘法还是加法,防止重复或遗漏。
