大型LED矩形阵列光斑照度的均匀性研究

刘启能， 刘 沁

(1. 重庆工商大学 重庆市检测控制集成系统工程实验室， 重庆 400067;2. 重庆工商大学 计算机科学与信息工程学院， 重庆 400067; 3. 重庆工商大学 设计艺术学院， 重庆 400067)

1 引 言

作为一种新型光源，发光二极管(LED)由于其发光效率高(节能)、使用寿命长已被广泛地使用于各种照明环境。怎样让这种新型的光源在照明领域内得到更充分的使用，发挥出更大的应用价值。这就促使人们越来越重视在理论上对LED照明特性进行研究[1-5]。近年来对LED照明特性的研究在很多方面都取得了成果，文献[6]对利用自由曲面透镜来实现单个LED光源的大视场角准直照明问题开展了研究，文献[7-8]对自由曲面重新配光来实现单个LED光源的均匀照明问题开展了研究。随着对LED光源照明特性的深入研究，人们把注意力放在了对LED阵列的照明特性的研究上，文献[9-11]对方形和圆形两种典型LED阵列的照明特性展开了研究，得出了其照明的变化规律和光斑的发散规律。文献[12-13]分别对LED圆形阵列和LED方形阵列照度的均匀性问题开展了研究，得出了LED圆形阵列和LED方形阵列照度的均匀度与阵列结构参数的关系。

目前对LED阵列照度均匀度的研究中还存在3个问题有待进一步深入：一是对光斑的范围没有做准确的定义，使得研究照度均匀度没有准确的范围；二是研究的对象仅是LED小型阵列(由一百个以内的LED灯芯构成的阵列)，而对大型LED矩形阵列(由一万个以上的LED灯芯构成的阵列)的照度均匀度问题没有做研究；三是仅对方形和圆形两种典型阵列的照度均匀度进行了研究，而对更一般的矩形阵列的照度均匀度问题未开展研究。而对现代的照明环境使用LED大型阵列的情况越来越多、越来越广，因此在理论上弄清大型LED矩形阵列这种非常具有代表性阵列的照度均匀度的变化规律有着重要的理论价值和应用价值。本文将对大型LED矩形阵列的照度均匀度展开研究，根据单个LED灯芯的照度公式以及大型LED矩形阵列在目标平面上照度分布的对称性，建立了研究大型LED矩形阵列光斑的照度均匀度的物理模型，推导出计算大型LED矩形阵列光斑的照度均匀度公式。利用该公式研究了大型LED矩形阵列照度均匀度随目标距离、矩形长宽比以及m值的变化规律。这些规律的获得为提高大型LED矩形阵列的照度均匀性提供了理论依据，也为大型LED矩形阵列的照度均匀性设计提供了研究方向和方法。

2 理论建立

LED大型圆形阵列的照度公式建立在单个LED芯片的照度公式的基础上。对于LED单个芯片，其视角θ与光强I由下式确定[14]：

I=I0cosmθ，

(1)

式中的m值由半角θ1/2决定(θ1/2为光强降为中心光强一半对应的视角)，I0为视角为0°方向的光强。LED芯片的m值根据制造工艺确定，由生产厂家提供。

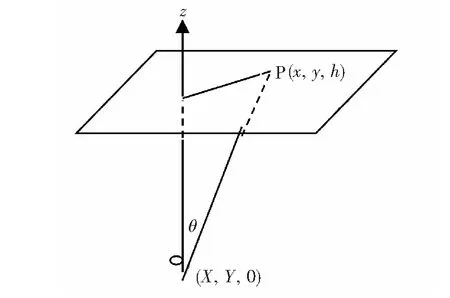
图1 单个LED芯片的照度

目标平面上的照明点P的坐标在(x,y,h)处，LED芯片的坐标为(X，Y,0)，见图1。在P点处LED芯片产生的照度E与光强I由下式确定[14]：

(2)

其中l为芯片到P点的距离。结合式(1)和式(2)，可得在P点处单个LED芯片产生的照度为：

(3)

如果在平面z=0上有N个LED芯片，由于N个LED芯片发出的光彼此为非相干光，因此它们发出光的叠加为非相干叠加，即在P点处产生的照度为：

E(x,y,h)=

(4)

其中Xn、Yn为第n个LED芯片的坐标。

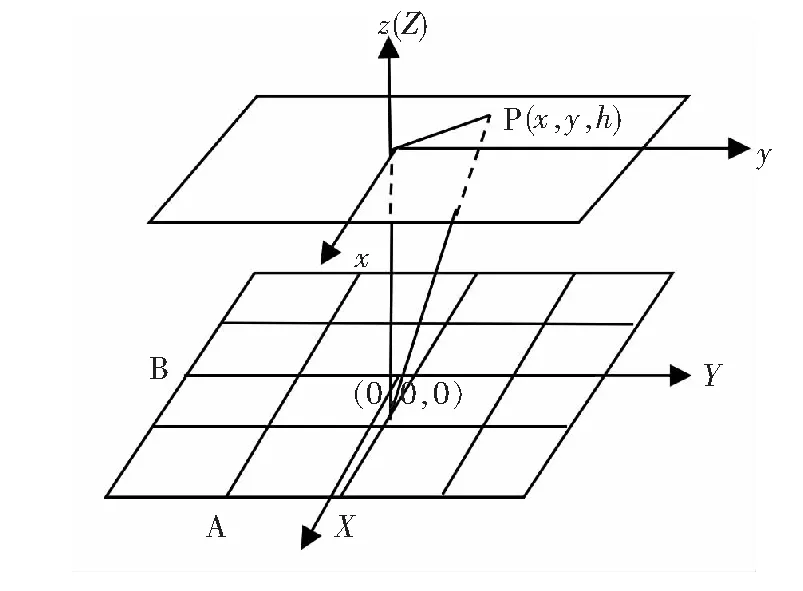
图2 大型LED矩形阵列的照度

下面研究的大型LED矩形阵列采用的设计为：矩形阵列的长边边长为A,平行于x轴；宽边边长为B，平行于y轴。将长边和宽边都用奇数M个点等分，构成矩形阵列网格。每个小矩形网格的长为a=A/(M+1)、宽为b=B/(M+1)。在该矩形阵列网格的每个节点上放置一个LED芯片，则该大型LED矩形阵列的LED芯片总数N=(M+2)×(M+2)。该大型LED矩形阵列放置于z=0平面内，阵列中心处的芯片的坐标在(0,0,0)处，目标平面为z=h,如图2。由(4)式可得在目标平面上P点该大型LED矩形阵列产生的照度为：

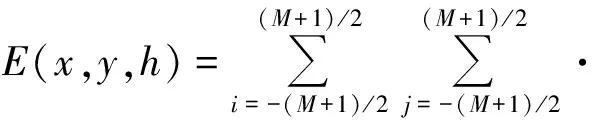
(5)

利用式(5)可以研究该大型LED矩形阵列在目标平面上光斑的照度规律。照度在目标平面上x轴和y轴上的公式分别为：

(6)

由于该大型LED矩形阵列芯片的分布相对于x轴、y轴以及z轴是对称的，所以阵列在目标平面产生的照度分布也是以z轴为对称轴。由对称性可知光斑的照度峰值出现在目标平面上的(0,0,h)处，由式(5)可得光斑的照度峰值E0满足：

(7)

对于聚光性较好的LED芯片，照度E大于光斑中心照度0.2E0的范围内汇集了90%以上的光通量。由此可以确定照度光斑的范围满足的关系为[9]：

E≥0.2E0，

(8)

由于该大型LED矩形阵列的芯片在x轴和y轴方向分布不同，因此其光斑边缘到光斑中心的距离在x轴和y轴上是不同的。设在x轴上光斑中心到光斑边缘的距离为Rx，在y轴上光斑中心到光斑边缘的距离为Ry,由式(6)和式(8)可得Rx和Ry满足方程：

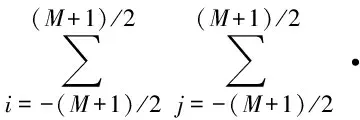
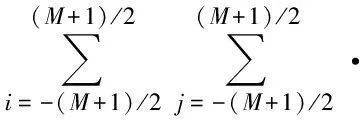
(9)

取M=99,则阵列的LED芯片总数N=101×101=10 201个，m=20,A=8 m，B=5 m，单个芯片的I0=2 cd。由式(5)、(6)、(9)计算出在目标距离h=10 m处光斑的形状以及在x轴和y轴上照度的分布曲线，如图3所示。由图3(a)可知，该阵列的光斑为椭圆。由图3(b)和图3(c)可知，照度在x轴和y轴上的分布具有对称性。

下面在上述光斑和照度分布的对称性基础上建立大型LED矩形阵列照度均匀度的评价方法。在文献[12-13]中建立的研究LED阵列照度均匀度的计算方法中，由于没有对光斑的区域作鉴定，再加上大型LED矩形阵列的灯芯数巨大，因此用文献[12-13]中的照度均匀度的计算方法来研究大型LED方形阵列照度均匀度会遇到困难。为了解决上述困难，首先在光斑和照度分布的对称性基础上建立照度均匀度u的概念。由于该阵列的光斑的对称性以及照度在x轴和y轴上的分布具有对称性，可以引入x轴和y轴上的照度均匀度ux和uy的概念来描述光斑内照度在x轴和y轴上的均匀程度，即：

(10)

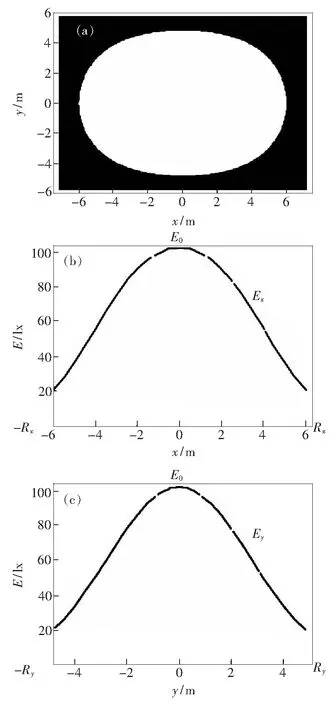
图3 大型LED矩形阵列的光斑和照度分布曲线

(11)

式(11)中ux和uy的几何意义是：在图3(b)和图3(c)中的照度曲线在光斑内的面积与照度峰值在光斑内的面积之比。ux和uy越大表明照度曲线在光斑内的面积越接近照度峰值在光斑内的面积，其照度的均匀性就越好。因此可以分别用ux和uy的大小来衡量照度在x轴和y轴上的均匀程度。但是ux和uy还不能准确地描述整个光斑内照度的均匀程度。为了描述整个光斑内照度的均匀程度，利用该阵列光斑照度的对称性，对ux和uy做光斑长度的加权平均，即：

(12)

式(12)中的u就能够描述该阵列的照度均匀程度，利用式(12)即可以研究大型LED矩形阵列的照度均匀度的变化规律。

3 照度均匀度

下面应用式(6)～(12)，利用数值计算法研究大型LED矩形阵列的照度均匀度随目标距离、矩形长宽比以及m值的变化规律。该大型LED矩形阵列仍取M=99,则阵列的LED芯片总数N=101×101=10 201个，单个芯片的I0=2 cd。

3.1 照度均匀度与目标距离的关系

固定m=20、长A=8 m、宽B=5 m(长宽比A/B=1.6)，取目标距离z为8，9，10，11，12，13，14，15，16，17 m 10组数据，计算出对应的照度均匀度ux、uy、u的数据，见表1。

利用表1中的数据绘出照度均匀度ux、uy、u随目标距离的响应曲线，如图4所示。在图4中实线、虚线、点划线分别为u、ux、uy随目标距离的响应曲线。由图4可知：目标距离对照度均匀度u、ux、uy都有明显的影响，照度均匀度u、ux、uy都随目标距离的增加而非线性地减小。当目标距离为8 m时，其照度均匀度u、ux、uy分别为0.687，0.707，0.661；当目标距离增大为17 m时，其照度均匀度u、ux、uy分别减小为0.649，0.652，0.645。 照度均匀度随目标距离变化的这一规律为提高大型LED矩形阵列照度均匀度的设计提供了方向，要想获得较好的照度均匀度其目标距离不能太远。

表1 不同目标距离下的照度均匀度ux、uy、u

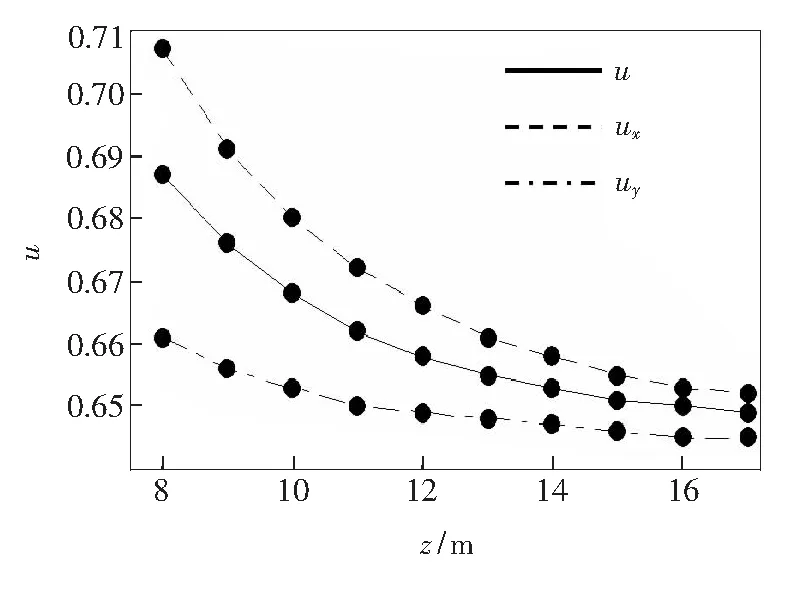
图4 均匀度随目标距离的响应曲线

3.2 照度均匀度与长宽比的关系

固定目标距离z=10 m、m=20、宽B=5 m。取长宽比A/B为1.1，1.2，1.3，1.4，1.5，1.6，1.7，1.8，1.9，2.0等10 组数据，计算出对应的照度均匀度ux、uy、u的数据，见表2。

表2 不同长宽比A/B下的照度均匀度ux、uy、u

利用表2中的数据绘出照度均匀度ux、uy、u随长宽比的响应曲线，如图5所示。在图5中，实线、虚线、点划线分别为u、ux、uy随长宽比的响应曲线。由图5可知：长宽比对照度均匀度u、ux有明显的影响，照度均匀度u、ux都随长宽比的增加而非线性地增大。当长宽比为1.1时，其照度均匀度u、ux分别为0.655，0.656；当长宽比增大为2.0时，其照度均匀度u、ux分别增大为0.684，0.705。 在图5中，uy不随长宽比的增加而变化，其原因是计算中其宽边B保持不变。照度均匀度随长宽比变化的这一规律为提高大型LED矩形阵列照度均匀度的设计提供了方向，要想获得较好的照度均匀度可以适当增加矩形阵列的长宽比。

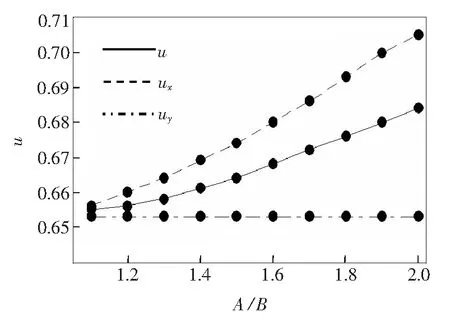
图5 均匀度随长宽比的响应曲线

3.3 照度均匀度与m值的关系

固定目标距离z=10 m、长A=8 m、宽B=5 m。取m=15，16，17，18，19，20，21，22，23，24，计算出对应的照度均匀度ux、uy、u的数据，见表3。

利用表3中的数据绘出照度均匀度ux、uy、u随m值的响应曲线，如图6所示。在图6中，实线、虚线、点划线分别为ux、uy、u随长宽比的响应曲线。由图6可知：m值对照度均匀度ux、uy、u有明显的影响，照度均匀度ux、uy、u都随m值的增加近似成线性地增大。当m值为15时，其照度均匀度ux、uy、u分别为0.660，0.669，0.649；当m值增大为24时，其照度均匀度ux、uy、u分别增大为0.674 5，0.689 1，0.655 8。照度均匀度随m值变化的这一规律为提高大型LED矩形阵列照度均匀度的设计提供了方向，要想获得较好的照度均匀度应该选择m值较大的芯片。

表3 不同m值下的照度均匀度ux、uy、u

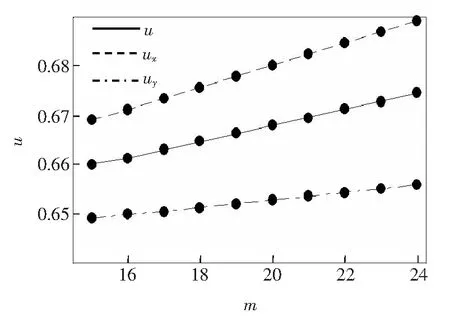
图6 均匀度随m值的响应曲线

4 结 论

应用LED灯芯的照度公式以及大型LED矩形阵列在目标平面上照度分布的对称性，建立了研究大型LED矩形阵列光斑的照度均匀度的物理模型，推导出计算大型LED矩形阵列光斑照度均匀度的公式。利用该公式研究了大型LED矩形阵列光斑的照度均匀度随目标距离、长宽比以及m值的变化规律。得出照度均匀度随目标距离的增加而非线性地减小；照度均匀度随长宽比的增加而非线性地增大；照度均匀度随m值的增加而近似成线性地增大。这些规律为提高大型LED矩形阵列的照度均匀性提供了理论依据，也为大型LED矩形阵列的照度均匀性设计提供了研究方向和计算方法，弥补了之前研究大型LED矩形阵列照度均匀性方法上的不足。

参 考 文 献：

[1] DING Y， LIU X， ZHENG Z R. Freeform LED lens foruniform illumination [J].Opt.Express, 2008, 16(17) :12958-12966.

[2] 苏宙平, 阙立志, 朱焯炜. 用于LED 光源准直的紧凑型光学系统设计 [J]. 激光与光电子学进展, 2012, 49(2):022203.

SU Z P, QUE L Z, ZHU Z W. Optical system design of the compact collimator for LED source [J].LaserOptoelectron.Prog., 2012, 49(2):022203. (in Chinese)

[3] SUN C C， CHEN C Y， HE H Y. Precise optical modeling for silicate-based white LEDs [J].Opt.Express, 2008, 16:20060.

[4] SUN C C， CHIEN W T， MORENO I. Analysis of the far-field region of LEDs [J].Opt.Express, 2009, 17(12):13918-13922.

[5] WANG K, LIU S， CHEN F，etal.. Freeform LED lens for rectangularly prescribed illumination [J].J.Opt. A-PureAppl.Opt., 2009, 11(10):105501-105505.

[6] 罗晓霞, 刘华, 卢振武, 等. 实现LED 准直照明的优化设计 [J]. 光子学报， 2011, 40(9):1351-1355.

LUO X X, LIU H, LU Z W,etal.. Automated optimization of free-form surface lens for LED collimation [J].ActaPhoton.Sinica, 2011, 40(9):1351-1355. (in Chinese)

[7] 丁毅， 顾培夫. 实现均匀照明的自由曲面反射器 [J]. 光学学报， 2007, 27(3):540-544.

DING Y, GU P F. Freeform reflector for uniform illumination [J].ActaOpt.Sinica, 2007, 27(3):540-544. (in Chinese)

[8] 丁毅， 郑臻荣, 顾培夫. 实现LED 照明的自由曲面透镜设计 [J]. 光子学报， 2009, 38(6):1486-1490.

DING Y, ZHENG Z R, GU P F. Freeform lens design foe LED illumination [J].ActaPhoton.Sinica, 2009, 38(6):1486-1490. (in Chinese)

[9] 刘沁， 刘启能. 方形LED阵列光斑发散特性的幂函数拟合 [J]. 光子学报， 2015, 44(1):56-60.

LIN Q, LIU Q N. Power function fitting methods of light spot divergence characteristics of LED square array [J].ActaPhoton.Sinica, 2015, 44(1):56-60. (in Chinese)

[10] 刘沁， 刘启能. 圆形LED阵列的光斑发散特性研究 [J]. 激光技术， 2015, 39(6):701-704.

LIN Q, LIU Q N. Divergence characteristics of light spot of LED roundness array [J].LaserTechnol.， 2015, 39(6):701-704. (in Chinese)

[11] 刘启能， 代洪霞. 幂函数拟合研究LED圆形阵列光斑的发散特性 [J]. 人工晶体学报， 2015， 44(5):685-689.

LIU Q N, DAI H X. Power function fitting methods of light spot divergence characteristics of LED circular array [J].J.Synth.Cryst., 2015, 44(5):685-689. (in Chinese)

[12] 王加文， 苏宙平， 袁志军, 等. LED 阵列模组化中的照度均匀性问题 [J]. 光子学报, 2014, 43(6):919-924.

WANG J W, SU Z P, YUAN Z J,etal.. Study on uniformity of LED array illumination distribution on target plane [J],ActaPhoton.Sinica, 2014, 43(6):919-924. (in Chinese)

[13] 赵芝璞， 季凌燕， 沈艳霞, 等. 基于PSO 粒子群算法的LED 照明系统光照均匀性研究 [J]. 发光学报， 2013, 34(12):1677-1681.

ZHAO Z P, JI L Y， SHEN Y X,etal.. Research of illumination uniformity for LED arrays based on PSO algorithm [J].Chin.J.Lumin., 2013, 34(12):1677-1681. (in Chinese)

[14] 姚家祎. 照明设计手册 [M]. 北京：中国电力出版社， 2006:187-188.

YAO J W.LightingDesignManual[M]. Beijing: China Power Press， 2006:187-188. (in Chinese)