动态参数调整的多策略差分进化算法

马永杰,朱 琳,田福泽

(西北师范大学 物理与电子工程学院，甘肃 兰州 730070)

差分进化算法(DE)[1]是由Storn等提出的一种简单高效的在连续空间内解决全局优化问题的进化算法，它借助于种群个体之间的差分信息对个体进行扰动，从而得到优秀的子代个体，通过不断进化，寻求问题的最优解．然而，在解决一些复杂的全局优化问题上，DE易出现收敛速度慢，早熟收敛甚至搜索停滞等问题．针对这些问题，许多学者相继提出了一些改进方案，用于提升DE算法的性能．

在对控制参数的研究方面，Brest等[2]提出了jDE算法，引入了两个新的控制参数τ1和τ2来自适应调整F和RC的值，从而提高算法的性能；Qin等[3]提出了SaDE算法，F和RC值借鉴前期产生优质解的经验进行自适应调整，在一定程度上提高了收敛速度；Zhang等[4]提出了JADE算法，F服从柯西分布，均值μF根据先前产生优质个体的F值取得；RC服从正态分布，均值μRC根据先前产生优质个体的RC值取得．这种自适应策略能够有效引导后代个体产生更加优质的解．在对变异策略的研究方面，Zhang等[4]发现了一种新的变异策略“DE/current-to-pbest/1”，该策略的应用提高了种群的多样性，使算法不易陷入局部最优；孔祥勇等[5]提出了全局加速的变异算子，避免了在较差个体周围的无用搜索，加速算法的全局收敛．Mallipeddi等[6]提出了EPSDE算法，采用突变策略集改进算法的性能．在对种群结构的研究方面，Ali等[7]提出了mDE-bES算法，将种群分成了四个大小相等的子种群，每隔一定代数后子种群间根据邻域拓扑结构进行迁移，有效改善了算法的寻优能力；Wu等[8]提出了MPEDE算法，种群被划分为3个同样小规模的指标种群和一个大规模的奖励种群，有效提高了种群的多样性，改善了算法的优化性能．

上述改进算法通过对参数调整，变异策略，种群结构的改进，取得了一定的效果，但是在一些优化问题上依然存在算法陷入局部最优，以及收敛速度慢等问题．因此，文中提出了一种动态参数调整的多策略差分进化算法(Multi-strategy differential evolutionary algorithm for dynamic parameter adjustment， MDADE)．该算法采用动态参数调整来提高算法的收敛性能；采取多种群多变异策略的进化方式避免种群陷入局部最优；采用择优保留的机制节省计算资源；采用多个子种群随机迁移的方式改善进化后期种群多样性较差的问题．为了验证所提算法的优势性，文中选取了CEC2005标准测试函数[9]对MDADE算法进行仿真实验．

1 基本DE算法

DE算法的基本流程为：首先在解的可行性范围内生成PN个D维的随机个体作为初始化种群，随后对当前种群进行变异操作，对应生成变异个体，再将变异后的个体通过交叉策略生成交叉个体，最后将交叉个体与变异个体进行选择筛选，两者中更优秀的个体进入下一代，构成新的种群．

在传统的DE算法中，根据变异向量生成方式的不同，可形成多种变异策略．每一种变异策略对于不同问题所表现的能力也有所差异．常见的变异策略有以下七种[10]：

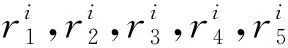
2 MDADE算法

2.1 动态参数调整

在差分进化的过程中有2个参数F和RC，它们的取值大小一定程度上影响着进化后个体的优劣．对于变异策略中的缩放因子F，在进化初期，个体的适应度值较差，F的值偏大会增加差分向量的扰动能力，扩大解的搜索范围，而在进化后期，F的值偏小会增加算法的局部寻优能力，使个体更大程度的接近最优解．对于交叉策略中的交叉概率RC，Storn等认为RC∈[0.8,1]的效果最好[1]．根据上述分析，文中采用以下方式进行动态参数调整．

其中,0FX为子种群X的初始均值；Gm为最大迭代次数；G为当前迭代次数．交叉概率RC则在[0.8,1]之间随机产生．

2.2 多变异策略

为了使算法适应不同的优化问题，MDADE算法采用3种变异策略应用于不同的子种群中以提高算法的性能．文中综合考虑了算法的局部寻优和全局搜索能力，选取了3种相应的变异策略．子种群X1选用的变异策略为“DE/rand/1”((1)式)，子种群X2选用的变异策略“DE/rand-to-best/1”((5)式)；子种群X3选用的变异策略为“DE/best/2”((4)式)．DE/rand/1的基向量为随机个体，能够扩大搜索范围，因此其具有较好的全局搜索能力；DE/rand-to-best/1的差分向量融合了最优向量和随机向量，在探索与开发中取得了一定的平衡；DE/best/2的基向量为最优个体，能够指引种群中的个体向全局最优处靠近，因此其具有较快的收敛速度．3个子种群采用3种不同的变异策略，使算法能够更好的适应不同的优化问题．

2.3 择优保留

在进化初期，变异交叉等操作会使种群迅速进化，此时的优秀个体更迭迅速不需要保留．但在经过一定代数的进化后，种群进化开始趋于缓慢，此时引进择优保留策略，使优秀个体不参与接下来的进化，其余个体则重新随机划分为3个子种群．之后每迭代一定代数，将所有个体重新排序，确定新的优秀个体进行保留，直至进化结束．文中选取的优秀个体数为9个，更新代数为20．

2.4 MDADE算法流程

MDADE算法的流程图如图1.

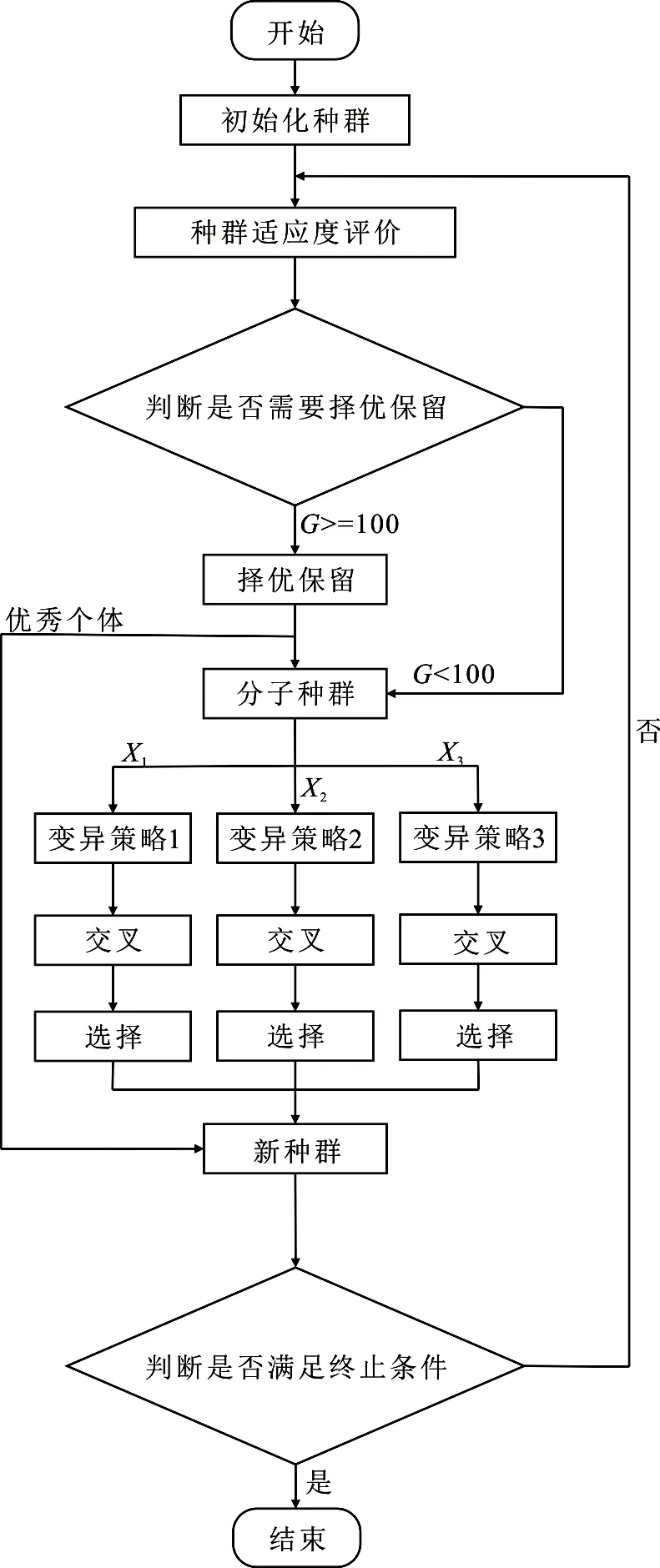
图1 MDADE算法流程图

3 实验结果与分析

3.1 MDADE算法与先进算法的比较分析

为了验证MDADE算法在CEC2005的25个标准测试函数上的性能，表1给出了MDADE算法与四个对比算法的仿真实验．它们分别是SaDE[3],EPSDE[6],SspDE[11]和MPEDE[8]，这些算法的参数设置遵循原始文献．文中算法的种群规模NP设置为60，F范围设置为(0,1)，最大函数评价次数MAX_FES设置为60000，0F1设置为0.4，0F2设置为0.3，0F3设置为0.2．每个算法都要针对30维标准测试函数独立运行25次，并记录各测试函数的均值和标准差的平均值，进行Wilcoxon符号秩检验，用以对比不同算法在统计学意义上是否存在显著差异．其中W代表Wilcoxon符号秩检验，“+”“-”“≈”分别表示文算法优于、差于、约等于对比算法．

文中选取的4种对比算法各有特点，SaDE算法中包含控制参数自适应；EPSDE算法选取了多种变异策略作为侯选池；SspDE算法提出了试验向量生成策略和自适应调整机制，而MPEDE算法则为较新的算法．通过与这4种改进算法的对比，可以有效验证本文算法所提出的动态参数调整机制和多变异策略的优势所在．由表1可见，MDADE算法在CEC2005的25个测试函数上整体表现较优，其中有20个优于SaDE，21个优于EPSDE，21个优于SspDE，17个优于MPEDE．

对于单峰函数(函数F1～F5)而言，算法在函数F1上表现欠佳，劣于SaDE算法和EPSDE算法，在函数F3上劣于MPEDE算法．在多峰函数(函数F6～F12)上，MDADE算法表现突出，只在F9上不如算法SaDE．而在复杂多峰函数和混合组成函数(函数F13～F25)上，本文算法都明显优于SaDE算法、EPSDE算法和SspDE算法，只在函数F15和F22上略差于MPEDE算法，可见文中算法在处理复杂优化问题上的优势．

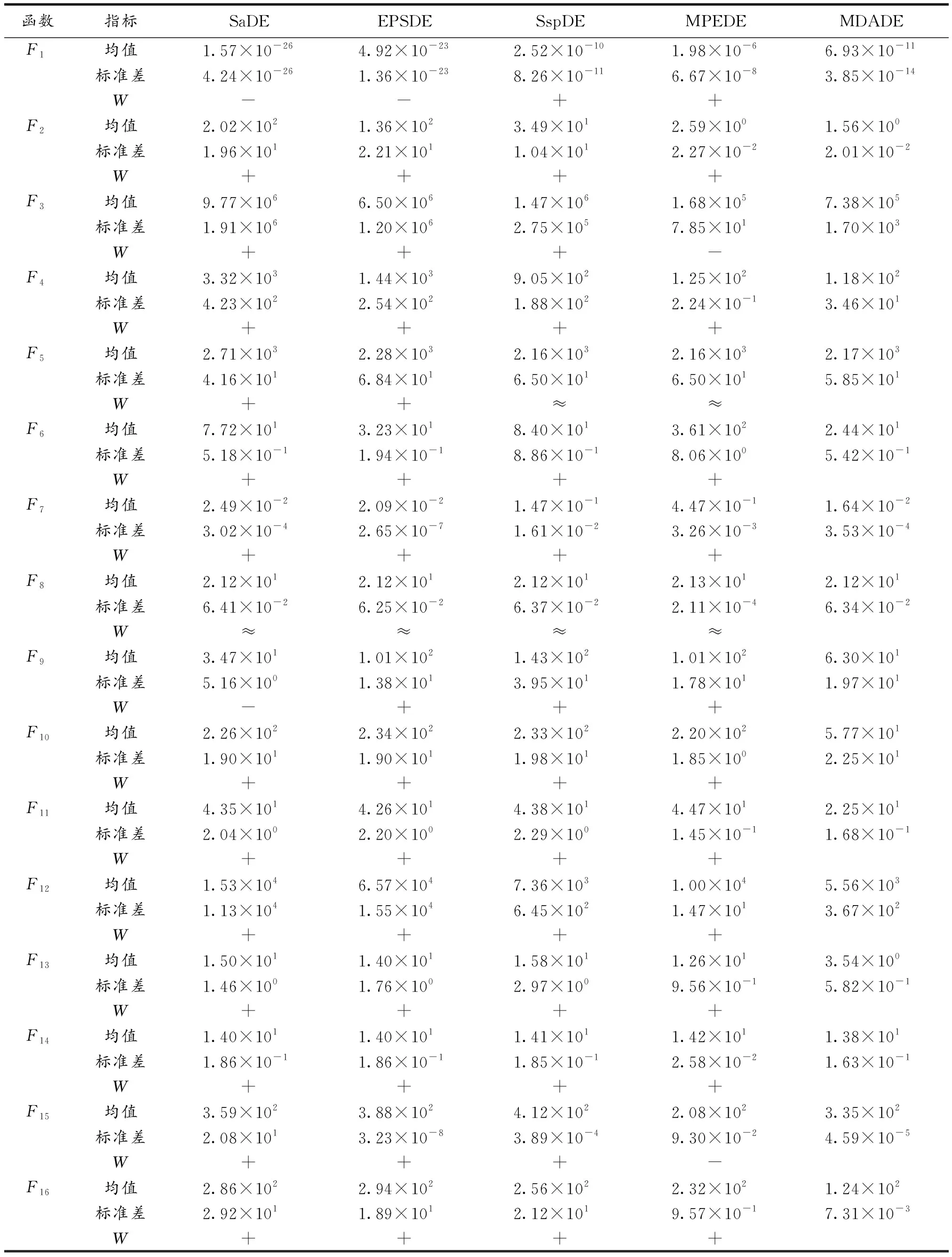
表1 5种算法测试结果比较(D=30)

续表1

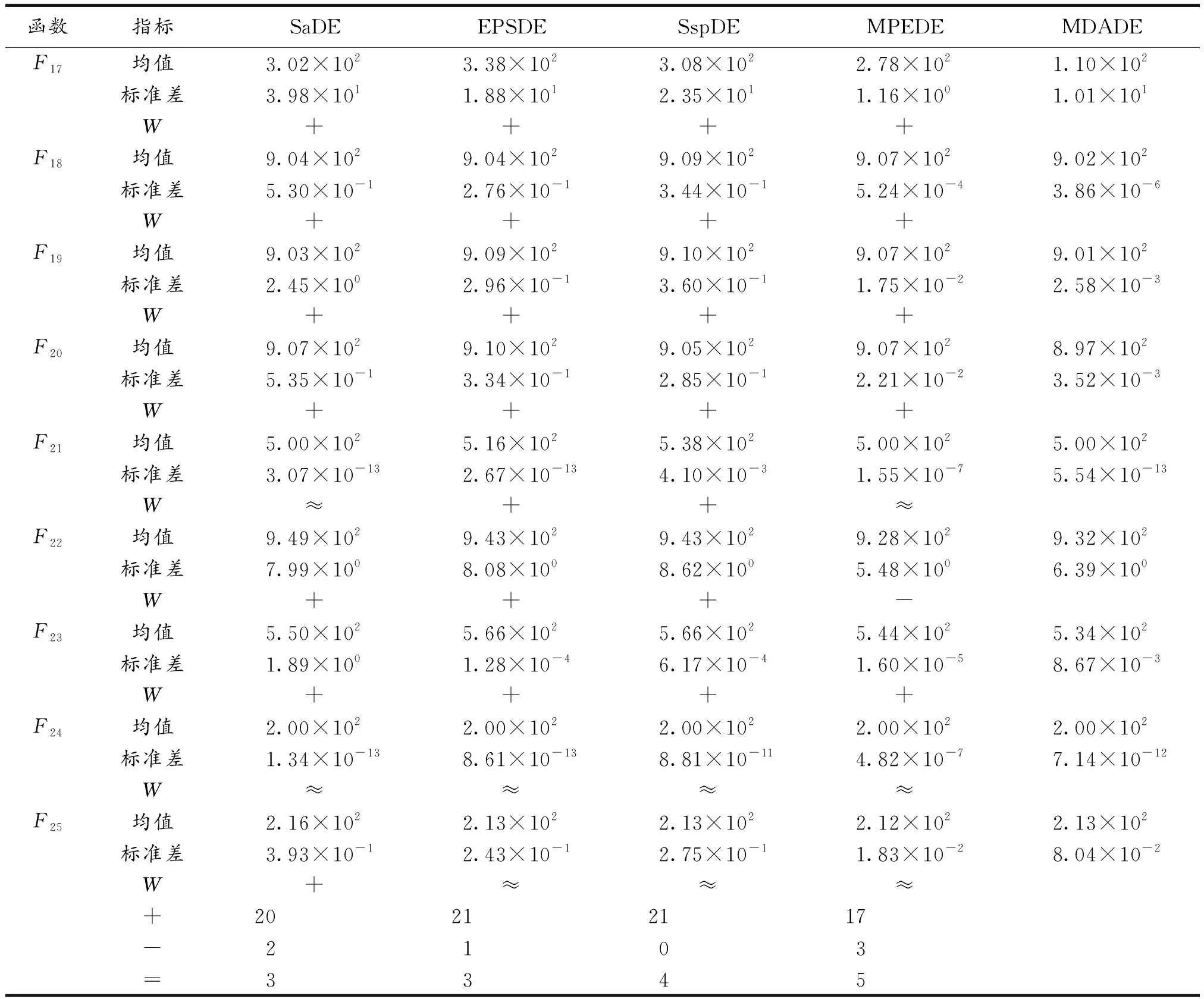
函数指标SaDEEPSDESspDEMPEDEMDADEF17均值3.02×1023.38×1023.08×1022.78×1021.10×102标准差3.98×1011.88×1012.35×1011.16×1001.01×101W++++F18均值9.04×1029.04×1029.09×1029.07×1029.02×102标准差5.30×10-12.76×10-13.44×10-15.24×10-43.86×10-6W++++F19均值9.03×1029.09×1029.10×1029.07×1029.01×102标准差2.45×1002.96×10-13.60×10-11.75×10-22.58×10-3W++++F20均值9.07×1029.10×1029.05×1029.07×1028.97×102标准差5.35×10-13.34×10-12.85×10-12.21×10-23.52×10-3W++++F21均值5.00×1025.16×1025.38×1025.00×1025.00×102标准差3.07×10-132.67×10-134.10×10-31.55×10-75.54×10-13W≈++≈F22均值9.49×1029.43×1029.43×1029.28×1029.32×102标准差7.99×1008.08×1008.62×1005.48×1006.39×100W+++-F23均值5.50×1025.66×1025.66×1025.44×1025.34×102标准差1.89×1001.28×10-46.17×10-41.60×10-58.67×10-3W++++F24均值2.00×1022.00×1022.00×1022.00×1022.00×102标准差1.34×10-138.61×10-138.81×10-114.82×10-77.14×10-12W≈≈≈≈F25均值2.16×1022.13×1022.13×1022.12×1022.13×102标准差3.93×10-12.43×10-12.75×10-11.83×10-28.04×10-2W+≈≈≈+20212117-2103=3345

3.2 MDADE算法的收敛性能分析

为了测试MDADE算法的收敛性能，本文挑选了三个具有代表性的测试函数，分别是F2,F11,F17．F2作为单峰函数的代表，F11作为多峰函数的代表，F17作为混合组成函数的代表．本文使用30维标准测试函数的实验结果绘制了收敛曲线．如图2～4所示,为了便于分析，3张图均采用对数坐标系，横轴表示函数评价次数，纵轴表示25次计算结果的均值．

由图2～4可看出，MDADE算法的收敛速度均快于其他4种算法，并且能够有效跳出局部最优值．从图3-4可以看出，所提算法的收敛曲线出现了拐点，证明算法有效的跳出了局部最优值．也由此可见MDADE算法之所以在复杂优化问题上表现突出，主要原因在于其跳出局部最优的能力，MDADE算法采用了多种群多变异策略协同进化，使算法适应更多更复杂的优化问题，采用的动态参数调整策略有效保证了算法的全局收敛性．

3.3 MDADE算法的变异策略分析

为了对MDADE算法的变异策略进行分析，文中采用单一变异策略与MDADE的3种变异策略协同进化相比较，以此来验证多策略变异的优势．对比结果如表2所示．

从表2中的数据可以看出，MDADE算法在25个标准测试函数中有15个函数获得了最好的结果，证明了多策略协同进化比单一策略的进化更具有优势．变异策略“DE/rand/1”在处理混合组成函数上表现突出，变异策略“DE/best/2”在处理单峰函数问题上表现较优，变异策略“DE/rand-to-best/1”则在个别多峰函数上优势明显，而3种变异策略协同进化之后，算法的整体性能有了明显的提升．多策略协同进化能有效的改善种群的多样性，同时避免了单一变异策略导致的算法陷入局部最优的情况．

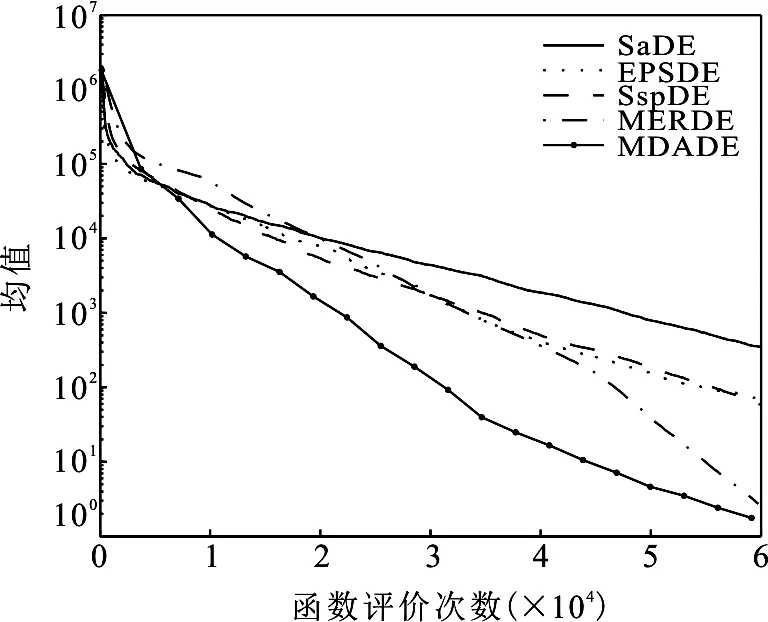
图2 5种算法对F2的寻优曲线图

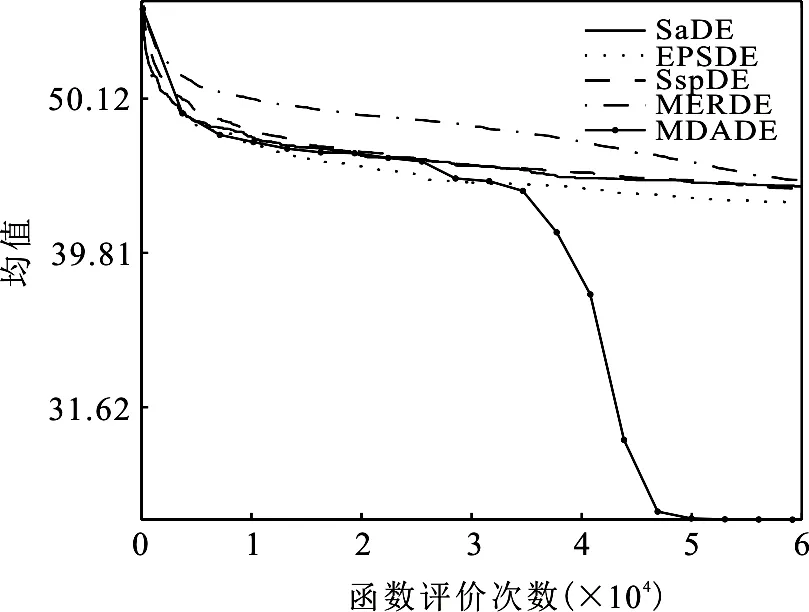
图3 5种算法对F11的寻优曲线图

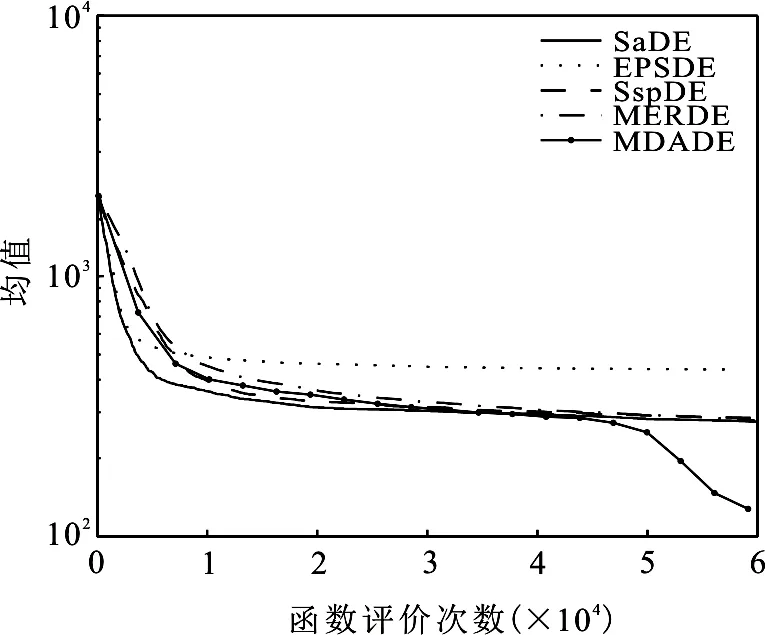
图4 5种算法对F17的寻优曲线图

函数rand/1rand-to-best/1best/2MDADEF13.72×10-81.51×1008.62×10-136.93×10-11F22.13×1025.96×1023.00×1001.56×100F32.40×1068.63×1061.02×1067.38×106F41.69×1034.23×1032.76×1031.18×102F52.48×1034.33×1042.20×1032.17×103F62.83×1022.52×1032.85×1012.44×101F79.42×10-16.92×1006.71×10-21.64×10-2F82.12×1012.12×1012.12×1012.12×101F92.55×1017.58×1016.74×1016.30×101F105.31×1015.13×1026.80×1015.77×101F112.35×1012.60×1012.65×1012.25×101F121.20×1043.03×1041.18×1045.56×103F138.19×1005.92×1003.55×1003.54×100F141.39×1011.36×1011.40×1011.38×101F153.80×1024.00×1024.11×1023.35×102F166.43×1011.28×1021.36×1021.24×102F171.99×1022.91×1021.22×1021.10×102F189.05×1029.23×1029.07×1029.02×102F199.07×1029.10×1029.08×1029.01×102F209.08×1029.03×1029.01×1028.97×102F215.00×1025.00×1025.00×1025.00×102F229.32×1029.47×1029.51×1029.32×102F235.34×1025.34×1025.49×1025.34×102F242.00×1022.00×1022.00×1022.00×102F252.14×1022.16×1022.14×1022.13×102

4 结束语

文中提出了一种动态参数调整的多策略差分进化算法(MDADE)．MDADE算法通过动态调整参数值，使算法更好的适应种群进化的不同时期，选取的多种变异策略有效避免了算法陷入局部最优，提出的择优保留机制减少了计算资源的浪费，同时也提高了算法的收敛速度．最后，通过在25个基准函数上的测试，验证了本文算法比一些优秀的改进算法收敛速度更快，收敛精度更高，算法性能明显优于对比算法，具有一定的竞争性．

:

[1] STORN R，PRICE K．Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces[J].Journalofglobaloptimization，1997，11(4)：341．

[2] BREST J，GREINER S，BOSKOVIC B，et al．Self-adapting control parameters in differential evolution： a comparative study on numerical benchmark problems[J].IEEETransonEvolutionaryComputation，2006，10(6)：646．

[3] QIN A K，HUANG V L，SUGANTHAN P N．Differential evolution algorithm with strategy adaptation for global numerical optimization[J].IEEETransonEvolutionaryComputation，2009，13(2)：398．

[4] ZHANG J．JADE：adaptive differential evolution with optional external archive[J].IEEETransonEvolutionaryComputation，2009，13(5)：945．

[5] 孔祥勇，高立群，欧阳海滨，等．求解大规模可靠性问题的改进差分进化算法[J].东北大学学报，2014，35(3)：328．

[6] MALLIPEDDI R，SUGANTHAN P N，PAN Q K，et al．Differential evolution algorithm with ensemble of parameters and mutation strategies[J].AppliedSoftComputing，2011，11：1679．

[7] ALI M Z，AWAD N H，SUGANTHAN P N．Multi-population differential evolution with balanced ensemble of mutation strategies for large-scale global optimization[J].AppliedSoftComputing，2015，33：304．

[8] WU G，MALLIPEDDI R，SUGANTHAN P N，et al．Differential evolution with multi-population based ensemble of mutation strategies[J].InformationSciences，2016，329：329．

[9] SUGANTHAN P N，HANSEN N，LIANG J J，et al．Problem definitions and evaluation criteria for the CEC 2005 special session on real-parameter optimization[C].KanGAL Report，2005．

[10] RAMMOHAN M,MINHO L．An evolving surrogate model-based differential evolution algorithm[J].AppliedSoftComputing，2015，34：770-787.

[11] PAN Q K，SUGANTHAN P N，WANG L，et al．A differential evolution algorithm with self-adapting strategy and control parameters[J].Computers&OperationsResearch，2011，38(1)：394．