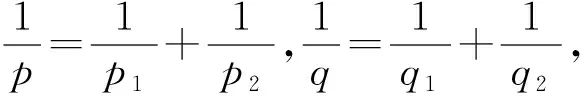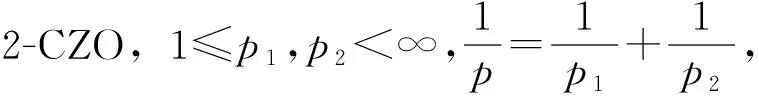多线性奇异积分算子在广义Morrey空间上的精确估计
2018-05-30周疆,胡喜
周 疆,胡 喜
(新疆大学 数学与系统科学学院,新疆 乌鲁木齐 830046)
0 引言
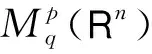
其中
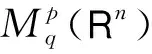
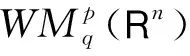
其中
设T是一个定义在m重Schwartz空间积S(Rn)上且取值于缓增分布空间S′(Rn)的多线性算子.算子T的分布核为(Rn)m+1去除对角线上元素有定义的函数K,使得
(1)
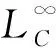
当y0,y1,…,ym不全等时,
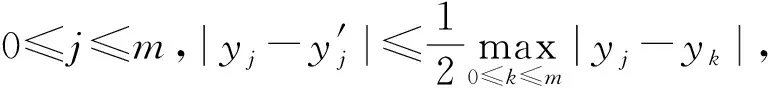
关于上述多重奇异积分已经有很多平行于经典的单线性理论的结果[9-13].事实上,对于这些算子,Grafakos等[9]得到:若对某些1 (2) (3) 其中Q是包含于Rn的方体,Q表示Rn中所有方体构成的集族,称上式右边为多Morrey范数.文献[14]通过具体例子说明多Morrey范数严格小于Morrey范数的乘积. 这样分环处理可以得到更精确的估计,详细的处理过程见后续证明. 下面先介绍一些相关的概念,并引入广义多范数Morrey空间的定义. 定义1[15]设Ψ=Ψ(r)是(0,∞)上正的增长函数,且对任意r>0满足倍测度条件:Ψ(2r)≤DΨ(r),这里D≥1是与r无关的常数.对于1≤q<∞,广义Morrey空间Lq,Ψ(Rn)定义为 其中 对于1≤q<∞,弱广义Morrey空间WLq,Ψ(Rn)定义为 其中 其中 弱广义Morrey空间WLq,Φ(Rn)定义为 其中 值得注意的是:Φ与Ψ有相同的性质,即Φ=Φ(r)是(0,∞)上正的增长函数,且对任意r>0满足倍测度条件:Φ(2r)≤DΦ(r),这里D≥1是与r无关的常数. (4) 式中f1,…,fm是定义在Rn上的可测函数. 其中 记aB(a>0)表示与B同中心边长伸缩a倍的球体;C表示与主要指标无关的常数,每次出现时其值可能并不相同;对于Rn中的可测子集E,用χE表示E的特征函数. 不失一般性,仅对T为2-CZO的情形叙述并证明. 证明利用Minkowski不等式,有 首先估计I1,利用多线性奇异积分算子的有界性,有 再由Φ的倍测度条件可得 下面估计I2,此时|x0-y1|+|x0-y2|≥4r.由于x∈B(x0,r),所以2|x-x0| <2r,再由三角不等式可知 进而有 再由Φ的倍测度性可得 综合I1和I2的估计可知 对上式左边取上确界即可证得结论. 】 当q1=q2=1时,有如下的弱性精确估计. 证明利用分布函数的性质,有 首先估计I1,利用多线性奇异积分算子的弱有界性,有 再由Φ的倍测度性可得 下面估计I2,利用切比雪夫不等式,有 再由Φ的倍测度性可得 综合I1和I2的估计可知 对上式左边取上确界即可证得结论. 】 : [1] MORREY C.On solutions of quasi-linear elliptic partial differential equations[J].TransactionsoftheAmericanMathematicalSociety,1938,43(1):126. [2] TAYLOR M E.Analysis on Morrey spaces and applications to Navier-Stokes and other evolution equations[J].CommunicationsinPartialDifferentialEquations,1992,17(9/10):1407. [3] OLSEN P A.Fractional integration Morrey spaces and a schrodinger equation[J].CommunicationsinPartialDifferentialEquations,1995,20(11/12):2005. [4] KUKAVICA I.Regularity for the Navier-Stokes equations with a solution in a Morrey space[J].IndianaUniversityMathematicsJournal,2008,57(6):2843. [5] ADAMS D R.A note on Riesz potentials[J].DukeMathematicalJournal,1975,42(4):765. [6] CHIARENZA F,FRASCA M.Morrey spaces and Hardy-Littlewood maximal function[J].RendicontidiMatematicaedellesueApplicazioni,1987,7(3):273. [7] DING Yong.A characterization of BMO via commutators for some operators[J].NortheasternMathematicalJournal,1997,13(4):422. [8] COIFMAN R R,MEYER Y.On commutators of singular integrals and bilinear singular integrals[J].TransactionsoftheAmericanMathematicalSociety,1975,212:315. [10] KENIG C E,STEIN E M.Multilinear estimates and fractional integration[J].MathematicalResearchLetters,1999,6(6):1. [12] CAI S,GARNEAU L,SAUVE R.Maximal operator and weighted norm inequalities for multilinear singular integrals[J].IndianaUniversityMathematicsJournal,2000,51(5):1261. [13] PEREZ C,TORRES R H.Sharp maximal function estimates for multilinear singular integrals[J].PublicationsMatematiques,2002,46(2):229. [14] LIDA T,SATO E,SAWANO Y,et al.Sharp bounds for multilinear fractional integral operators on Morrey type spaces[J].Positivity,2012,16(2):339. [15] XIAO Yu,TAO Xiang-xing.Boundedness of multilinear operators on generalized Morrey spaces[J].AppliedMathematics-AJournalofChineseUniversities:B,2014,29(2):127.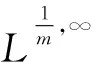
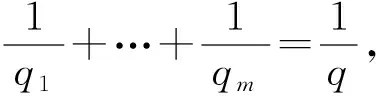
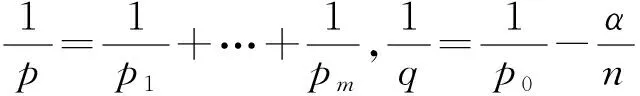
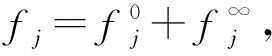
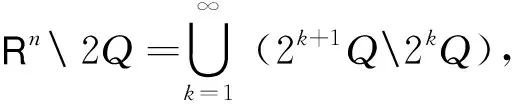
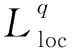
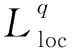
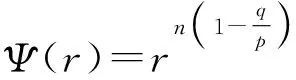
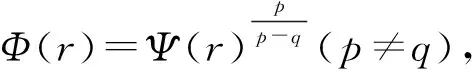
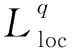
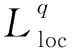
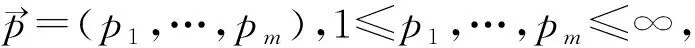
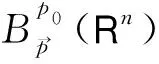
1 主要定理及其证明