函数的不等式
2018-05-30蔺友江
蔺友江
(重庆工商大学 数学与统计学院,重庆 400067)
1 主要结论

(1)

(2)
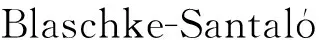
(3)
其中
(4)
在(3)式中,当p→∞时,有
(5)
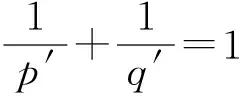
(6)
其中Γ*pK是K的Lp质心体的极体.利用度规函数Γ*pK可定义为
(7)
由于
(8)
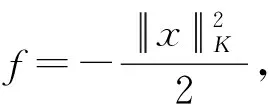
推论1[11]如果K是Rn中一个关于原点的星体,那么对于1≤p≤∞,有
V(K)V(Γ*pK)≤V2(Bn).
(9)
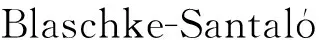
2 主要结论的证明

(10)
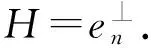
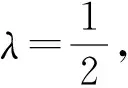
其中y1(yn)表示关于yn的函数.
关于Sf的Lp形式的Steiner对称化,对于固定的xn则有
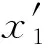
(14)
根据(14)式和Prekopa-Leindler不等式,结合Lpf的偶性可得
因此,根据Fubini定理可知原命题成立. 】

(15)
证明根据球面坐标变换可得
(16)
其中dω表示单位球面上的Hausdorff测度.
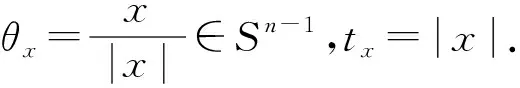
因此
(17)
对于r∈[0,∞),令f1(r)=exp(-h(r))rn-1,f2(r)=exp(-Lph(r))rn-1,f3(r)=exp(-r2/2)rn-1. 再令gi(t)=fi(et)et,i=1,2,3,那么
并且对于任意的s,t∈R,有
g1(s)g2(t)≤(g3(s/2+t/2))2.
根据Prekopa-Leindler不等式可得
根据(17)式可得
其中ωn=nπn/2/Γ(1+n/2)是欧式单位球的表面积. 】
定理1的证明根据引理1和Steiner对称化的积分不变性,可得
(19)
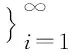
】
:
[2] GARDNER R J.The Brunn-Minkowski inequality[J].BullAmerMathSoc,2002,39(3):355.
[3] SCHNEIDER R.ConvexBodies:TheBrunn-MinkowskiTheory[M].Cambridge:Cambridge University Press,1993.
[4] BURCHARD A.Steiner symmetrization is continuous inW1,p[J].GeomFunctAnal,1997,7(5):823.
[5] CIANCHI A,FUSCO N.Steiner symmetric extremals in Polya-Szego type inequalities[J].AdvMath,2006,203(2):673.
[6] GARDNER R J.Symmetrals and X-rays of planar convex bodies[J].ArchMath(Basel),1983,41(2):183.
[10] LIN You-jiang.A new approach to Steiner symmetrization of coercive convex functions[J].JClassicalAnal,2017,11(2):129.