具有有限X-余分解维数的模的上同调性质

张翠萍,王鹏飞

(西北师范大学 数学与统计学院,甘肃 兰州 730070)

0 引言

1969年,Auslander等[1]在双边Noether环R上引入了有限生成模M的Gorenstein 维数G-dimRM,并证明了G-dimRM≤pdRM(当pdRM<∞时,等号成立).他们还证明了广义Auslander-Buchshaum公式.1995年,Enochs等[2]在任意环R上引入了Gorenstein投射模和Gorenstein投射维数GpdRM的概念,并研究了这类模的相关同调性质.称左R模M是Gorenstein投射的,如果存在一个HomR(-,Q)正合的正合列…→P1→P0→P0→P1→…,使得M≅Ker(P0→P0),其中Q,Pi(i=0,1…)是投射左R-模.记GpdRM=inf{n∈Z|存在正合列0→Gn→Gn-1→…→G1→G0→M→0,Gi是Gorenstein投射模,i=0,1,2,…,n}.如果这种正合列不存在,则规定GpdRM=∞.2010年,Bennis等[3]引入了X-Gorenstein投射模的概念；2014年,Zhu[4]引入了Abel范畴的拟可解子范畴X的概念,并给出了X-投射维数有限的模的几种等价条件.随着X的不同选取,X-Gorenstein投射模涵盖了Gorenstein投射模[2]、Ding 投射模[5]和Gorenstein-AC投射模.2014年,Emmanouit等[6]给出了Gorenstein投射维数有限的模的几种等价条件,利用这些条件研究了有有限Gorenstein投射维数的模相对于有有限投射维数的模的稳定性以及相对于Gorenstein投射模的稳定性.受此启发,对于模类X和W,文引入X-余分解维数和W-余分解维数的概念,给出了左R-模M的X-余分解维数有限的几种等价刻画,并研究了这类模相对于有有限W-余分解维数的模的稳定性以及相对于模类X的稳定性.

以下R指有单位元的结合环,模指左R-模.

1 模的X-余分解维数

本节主要介绍与本文相关的一些定义和结论.

定义1设X是R-模类,称X是余可解模类,如果满足下列条件:

(1)X关于扩张封闭,即对任意R-模的短正合列0→A→B→C→0,若A,C∈X,则B∈X.

(2)X关于单同态余核封闭,即对任意R-模的短正合列0→A→B→C→0,若A,B∈X,则C∈X.

(3)X关于有限直和与直和项封闭.

定义2设W是X的一个子类.称W是X的投射生成子,如果下列条件满足:

(1)对于任意X∈X,存在R-模短正合列0→X′ →W→X→0,其中W∈W,X′∈X.

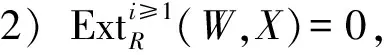
(3)W关于有限直和封闭.

定义3设X是余可解模类,M是R-模.称正合列

0→M→X0→X1→…→Xn-1→Xn→…

为M的X-余分解,其中Xi∈X(i=0,1,2,…).M的X-余分解维数(记为X-coresdimRM)定义为:X-coresdimRM=inf{n∈Z|存在正合列0→M→X0→X1→…→Xn-1→Xn→0,Xi∈X,i=0,1,2,…,n}.如果这种余分解不存在,则规定X-coresdimRM=∞.

类似地,可以定义M的W-余分解及其维数.

以下X指余可解R-模类,W指X的投射生成子类.

命题1设n是非负整数，则对任意的R-模M,以下结论等价:

(1)X-coresdimRM≤n.

(2)存在R-模短正合列0→M→X→W→0,其中W-coresdimRW≤n-1,X∈X.

(3)存在R-模短正合列0→X→W′→M→0,其中W-coresdimRW′≤n,X∈X.

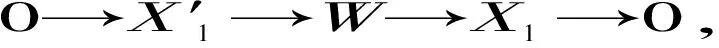
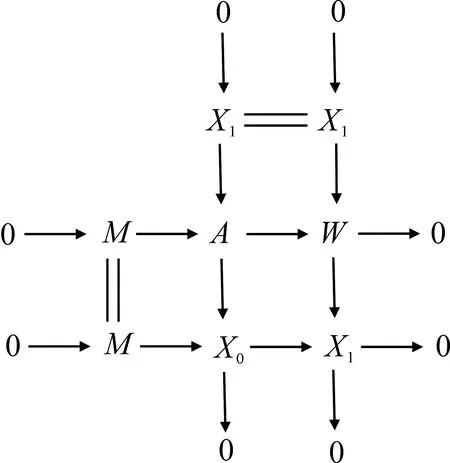
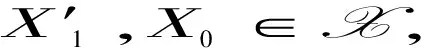
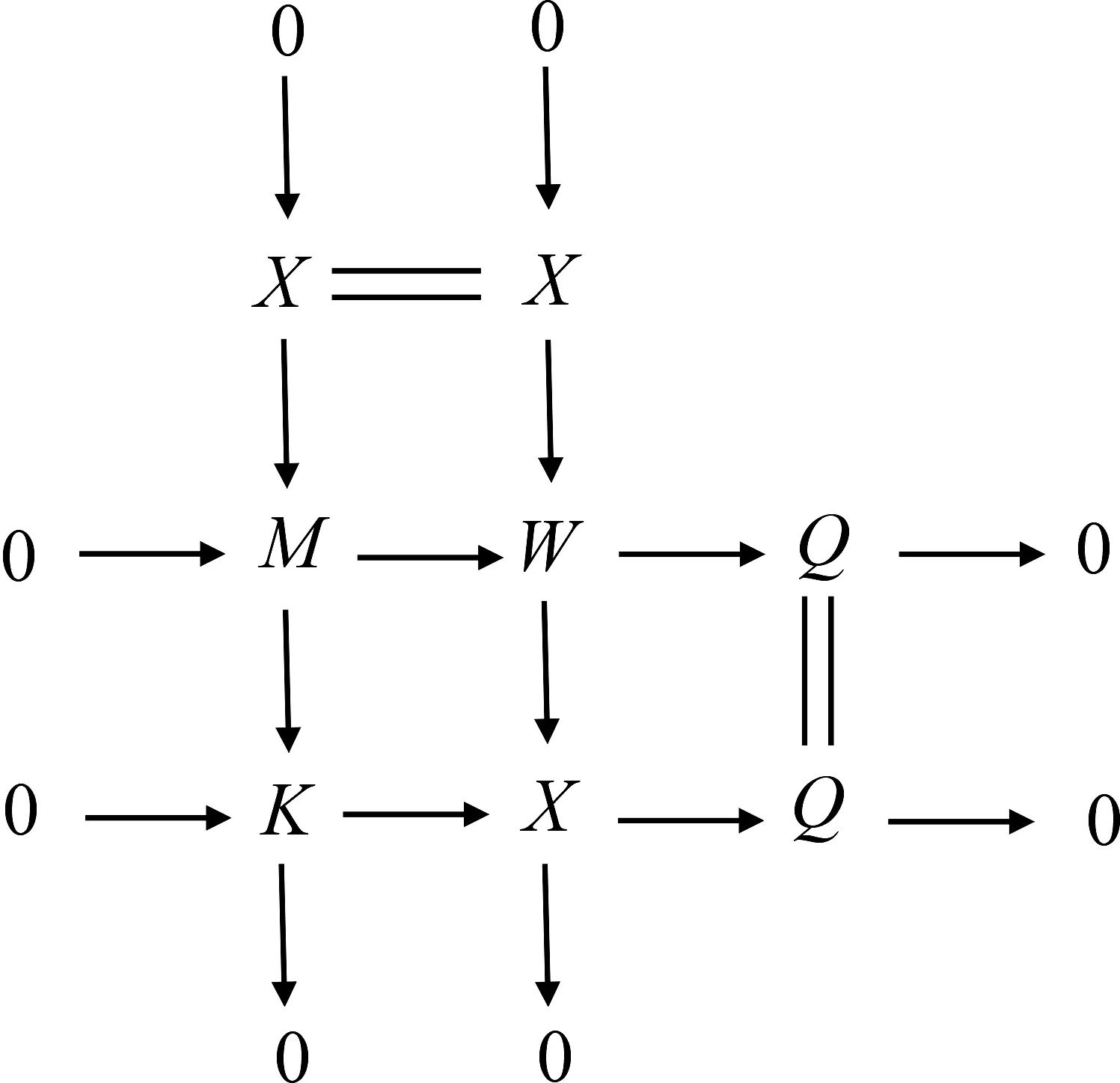
由上图第二行短正合列知W-coresdimRM′≤n-1.最后考虑以下拉回图:

因为X′,X∈X，从而V′∈X,故第二列即为所需短正合列.

(2)⟹(1).显然.

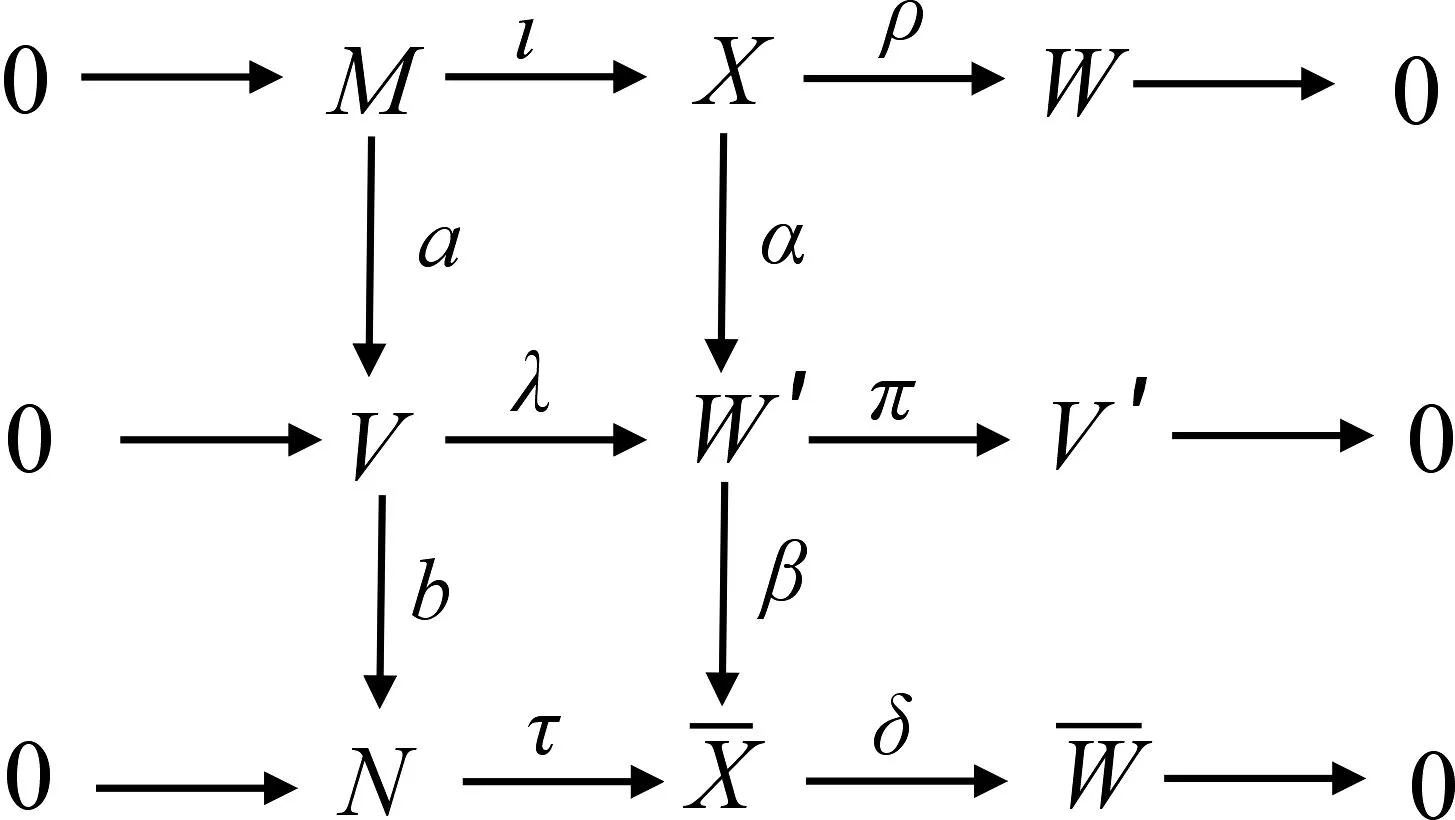
(2)⟹(3).假设存在短正合列0→M→X→W→0,其中X∈X,W-coresdimRW≤n-1.因为W是X的投射生成子类,故存在短正合列0→X′→W′→X→0,其中X′∈X,W′∈W.考虑以下拉回图:

因为W-coresdimRW≤n-1,因此W-coresdimRM′≤n,第一列即为所需短正合列.

(3)⟹(2).假设存在短正合列0→X″→W′→M→0,其中W-coresdimRW′≤n,X″∈X.由W-coresdimRW′≤n可知，存在短正合列0→W′→X→W″→0,其中W-coresdimRW″≤n-1,X∈W.考虑以下推出图:

因为X″,X∈X,从而M′∈X,故第三列即为所需短正合列. 】

命题2设R-模M的X-余分解维数有限.

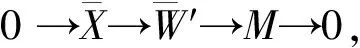
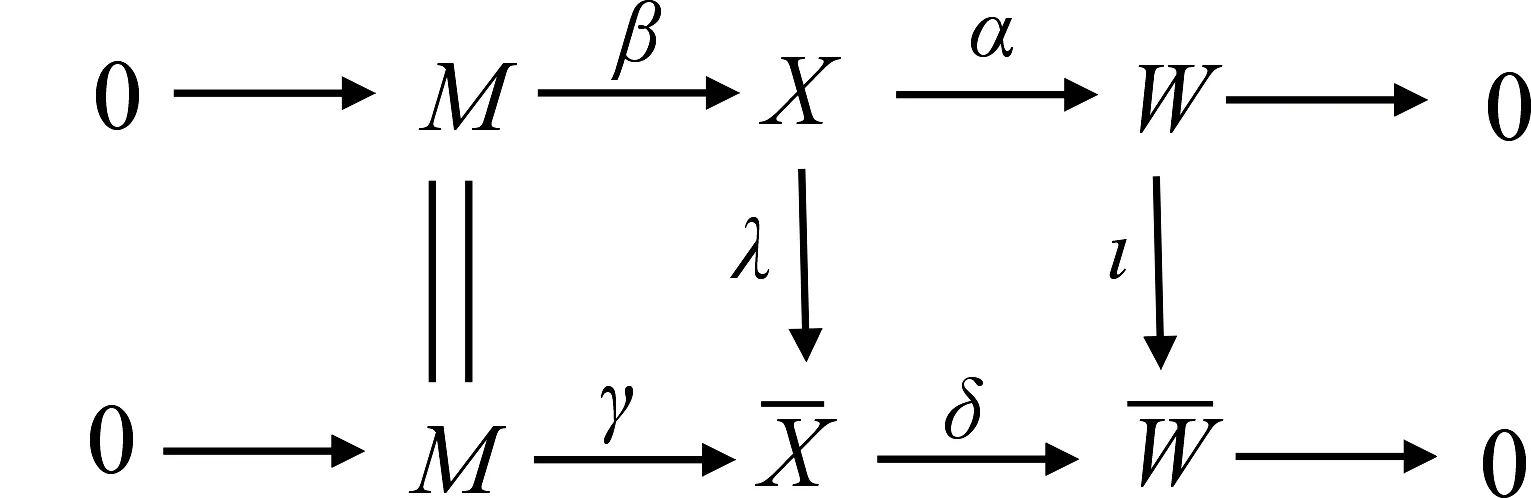
同理,存在λ′,ι′使下图交换：

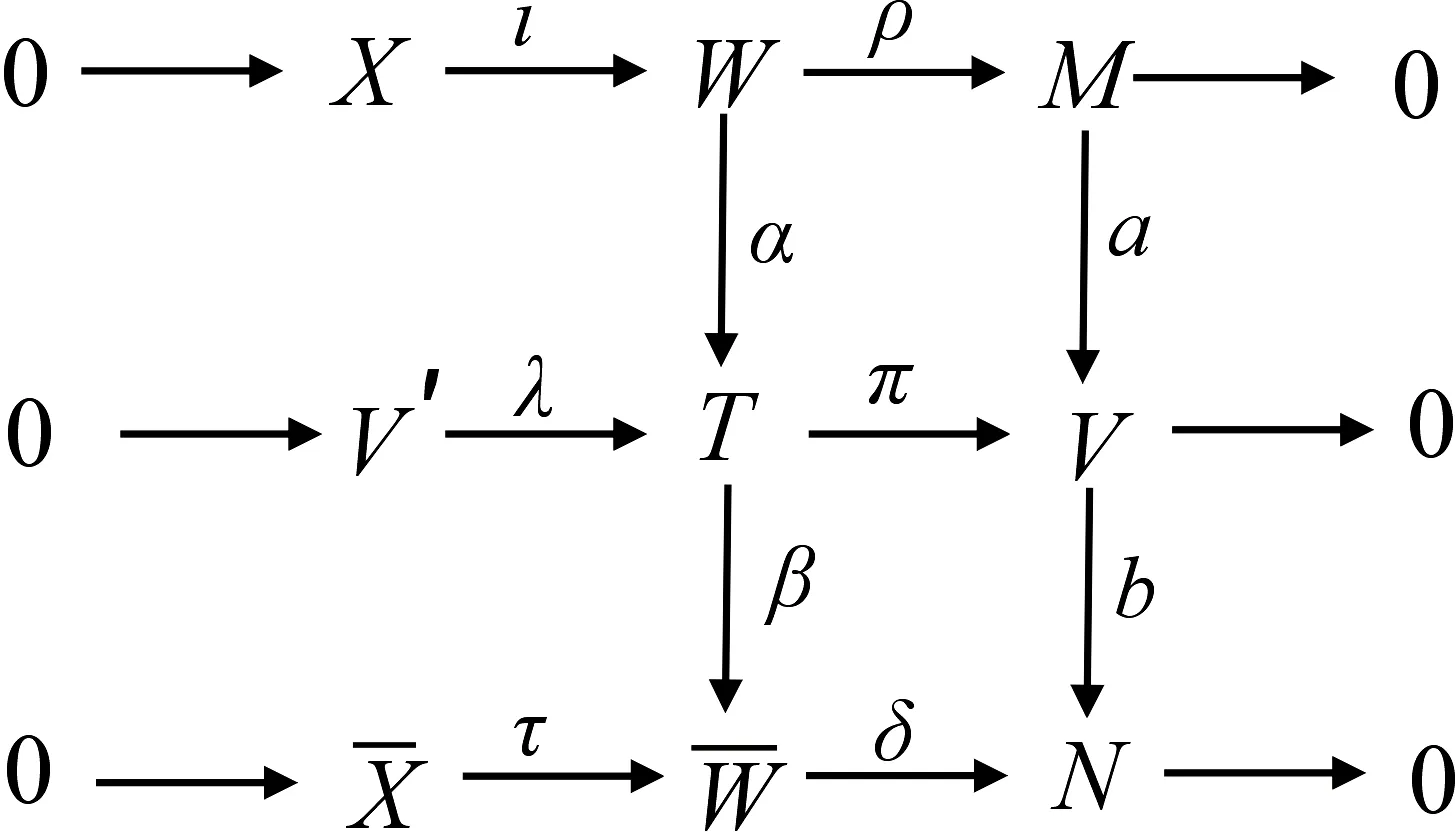
考虑以下交换图:

(2)证明与(1)类似. 】

2 相对于有限W-余分解维数的模的稳定性

设M,N是R-模,易得集合H={f:M→N|f可通过一个有有限W-余分解维数的R-模分解}是Abel群HomR(M,N)的子群.令W-HomR(M,N)表示商群HomR(M,N)/H, [f]W=[f]表示f所在的剩余类,其中f∈HomR(M,N).

引理1设M,N,L是R-模,则χ:W-HomR(N,L)×W-HomR(M,N)→W-HomR(M,L),χ([f],[g] )=[fg]是映射.

现在假设W-R-Mod的对象为所有R-模做成的类,对象M到N的态射集为W-HomR(M,N),态射的合成为引理1中定义的合成,则W-R-Mod为范畴.

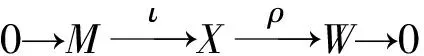
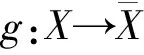
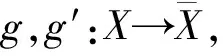
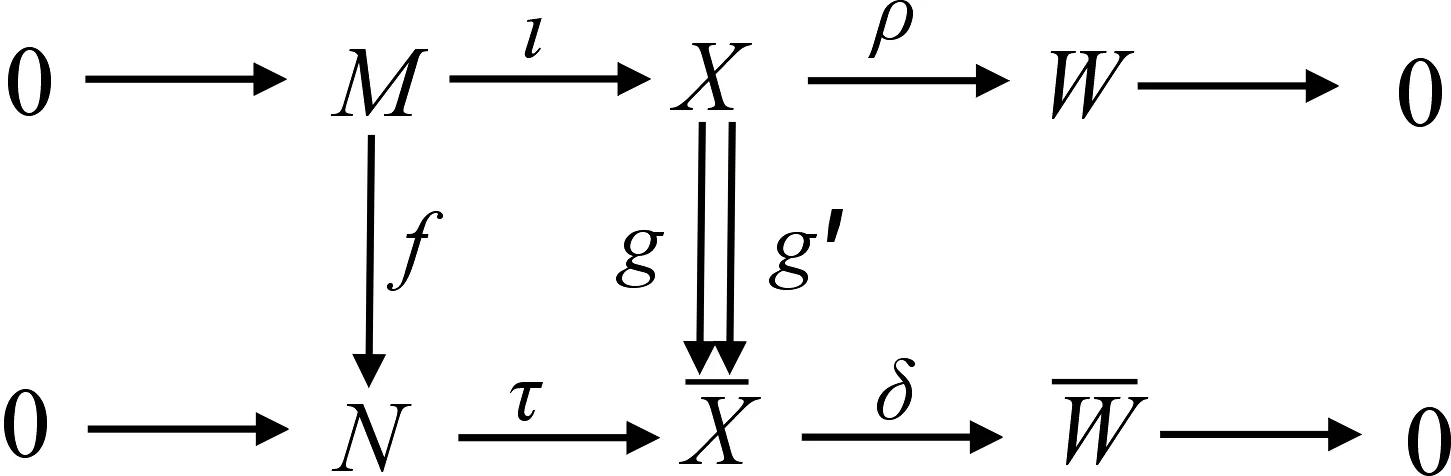
定理1函子μ是μ′的左伴随对.

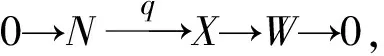
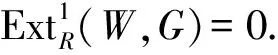
易得[q]*是满的.

设g∈HomR(X,G),使得[q]* ([g])=[0]∈W-HomR(N,G),即[gq]=[0].考虑以下交换图:

由引理2(3)知[g]=[0]∈W-HomR(X,G),从而[q]*是单的,所以[q]*是一一映射,即W-HomR(μ(N),G)≅W-HomR(N,μ′(G)).故μ是μ′的左伴随对. 】

3 相对于模类X的稳定性

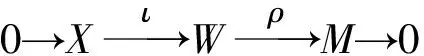
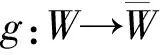
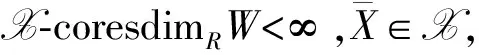
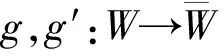
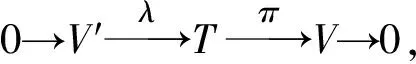
定理2函子μ是μ′的右伴随对.

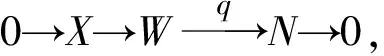
[q]*:X-HomR(G,W)→X-HomR(G,N)

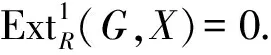
易得[q]*是满的.

设g∈HomR(G,W),使得[q]*([g])=[0]∈X-HomR(G,W),即[qg]=[0].考虑以下交换图:

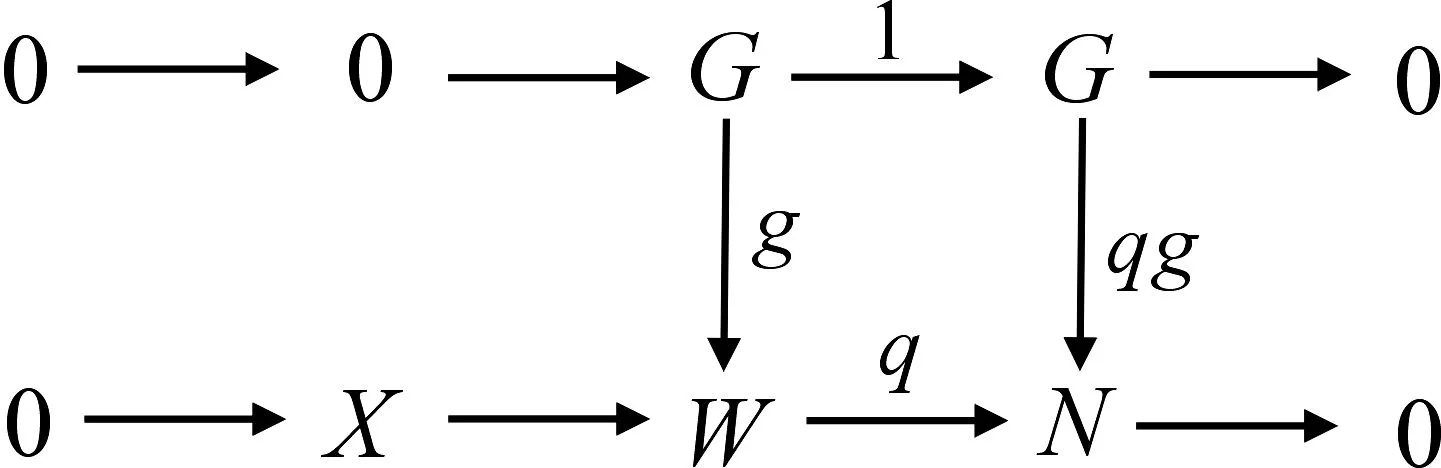
由引理3(3)知[g]=[0]∈W-HomR(G,W),从而[q]*是单的,所以[q]*是一一映射,即W-HomR(G,μ(N))≅W-HomR(μ′(G),N).故μ是μ′的右伴随对. 】

参考文献:

[1] AUSLANDER M,BRIDGER M.StableModuleTheory[M].Memoirs of American Mathematical Soc,1969.

[2] EDGAR E E,JENDA O M G.Gorenstein injective and projective modules[J].MathZ,1995,220(1):611.

[3] BENNIS D,OUARGHI K.X-Gorenstein projective modules[J].JournalofLanzhouUniversityofTechnology,2010(9-12):487.

[4] ZHU X.The homological theory of quasi-resolving subcategories[J].JAlgebra,2014,414:6.

[5] DING N Q,LI Y L,MAO L X.Strongly Gorenstein flat modules[J].JAustralMathSoc,2009,86(3):323.

[6] EMMANOUIL I,TALELLI O.Finiteness criteria in Gorenstein homological algebra[J].TransAmerMathSoc,2014,366(12):6329.