二阶层级自相似六边形蜂窝的面内压缩行为

于国际，李飞鹏，李世强,2，吴桂英

(1.太原理工大学 a.应用力学与生物医学工程研究所，材料强度与结构冲击山西省重点实验室，b.材料科学与工程学院，太原 030024；2.湖南大学 汽车车身先进设计制造国家重点实验室，长沙 410082)

在自然界不同的环境中，自然选择和进化产生了大量的多功能生物材料，由于这些材料通常都包含大量不同尺度的微孔层级结构，使其具有了优越的力学特性[1]，吸引了许多研究者的关注，也为现代工程结构优化提供了宽广的设计思路。人工层级材料的应用可追溯到埃菲尔铁塔的修建工程中[2]，其网状钢架层级结构不仅相对密度较低而且具有很高的整体强度。随着高新技术的发展及材料/结构一体化设计新理念的日渐成熟， 兼备轻质吸能和其他多种优异性能的人工层级材料(如图1所示)已被广泛应用于航空航天、高速运载(新型节能汽车、动车)、国防工程等高技术领域。

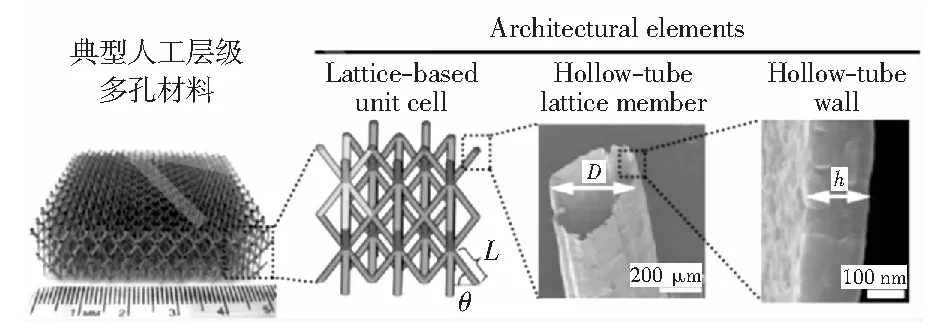
图1 层级点阵多孔材料各阶细观、微观结构[2]Fig.1 Microstructure of hierarchical lattice porous material[2]

蜂窝铝是以铝合金为基体的多孔金属材料，作为一种吸能缓冲的功能材料已获得了广泛的研究[3]，GIBSON et al[4]系统的研究了蜂窝的面内准静态压缩力学性能,指出蜂窝铝在面内压缩时孔壁会首先出现弯曲，产生线弹性变形，并且随着应变的增加，弹性弯曲、塑性屈服、蠕变或脆性断裂等现象会导致胞孔的坍塌；当相对的胞孔壁相互接触时，胞孔坍塌结束。影响蜂窝面内力学性能的参数主要包括孔径大小、壁厚以及基体材料的性质。由于其胞孔的可设计性，其最大优点是可根据不同需求对芯层胞孔微结构和尺度进行多样化设计，改善结构力学性能[5-7]。LAKES[8]指出相同质量下，二阶层级蜂窝的压缩强度是传统蜂窝的3～4倍。YIN et al[9-10]通过对两种不同的层级角锥点阵夹芯板进行面外压缩试验，分别给出了“拉-拉组合(stretch-stretch-hybrid)”和“拉-弯组合(stretch-bend-hybrid)”层级芯层的变形失效模式图，实验中发现拉-弯联合屈服的层级芯层主要有芯层面板起皱和芯层整体剪切变形两种模式；拉-拉联合屈服的层级芯层主要有芯层支撑屈曲、芯层面板屈曲、芯层面板压溃、芯层桁架欧拉屈曲以及芯层桁架剪切屈曲五种失效模式。在此基础研究者根据其构造的变形机制图对复合角锥点阵(CPL)芯层做了进一步优化设计，通过研究发现点阵桁架细观形状对层级结构力学响应影响较小，在同样的相对密度下，层级CPL芯层的强度是普通矩形截面点阵桁架芯层的5倍。CHEN et al[11]通过对传统蜂窝胞孔壁进行三角形点阵层级设计，研究二阶层级蜂窝面内压缩力学行为，提出两尺度方法计算二阶层级蜂窝的平台应力，给出了面内准静态压溃与动态冲击的平台应力表达式，指出层级结构能够提高蜂窝结构的平台应力。

本文通过对传统正六边形蜂窝胞孔的自相似层级设计，获得了二阶层级自相似六边形蜂窝结构，并利用商业有限元软件ABAQUS对其受面内载荷时的压缩行为进行了研究，分析了面内压缩变形模式及冲击速度对其变形模式的影响，并提出了准静态变形模式以及冲击模式下，面内x与y方向压缩变形的理论模型。

1 有限元模型

1.1 层级蜂窝有限元模型

通过对传统正六边形蜂窝的胞壁进行自相似层级设计，获得了二阶层级自相似六边形蜂窝，其胞元如图2(a)所示，一阶胞孔孔壁由6个二阶六边形蜂窝胞孔构成。层级蜂窝上下设置两块带有集中质量的刚性板，下端的刚性板固定，上端的刚性板以恒定的速度v冲击蜂窝，采用四节点壳单元(S4R)对层级蜂窝进行网格划分。x方向加载时冲击方向取16个一阶胞元，另一方向取9个一阶胞元，如图2(b)所示。y方向加载时冲击方向取15个一阶胞元，另一方向取9个一阶胞元，如图2(c)所示。层级蜂窝的一阶胞孔尺寸为L，二阶胞孔尺寸为l，二阶胞孔孔壁厚度为h，面外厚度为b.蜂窝的基体材料采用理想弹塑性模型，密度为ρs=2 700 kg/m3，弹性模量E=70 GPa，屈服强度σys=75 MPa，泊松比υ=0.3.

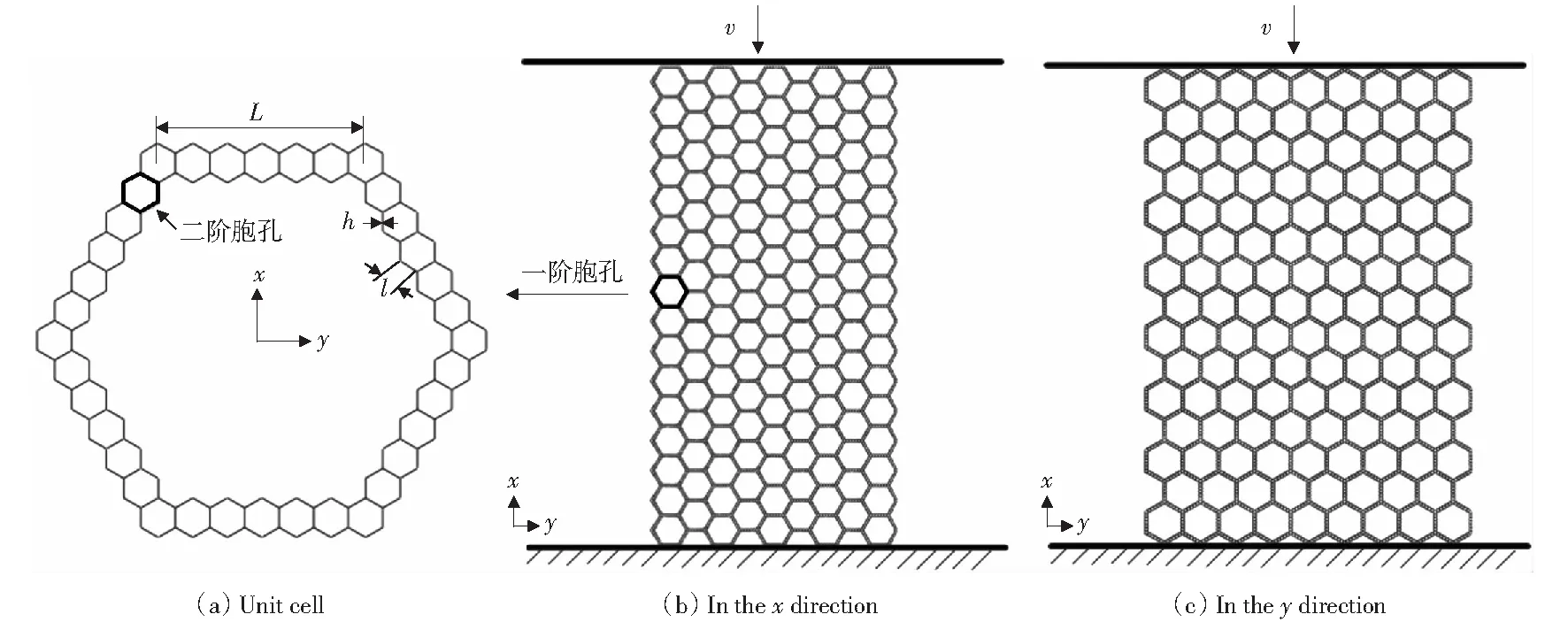
图2 蜂窝面内冲击示意图Fig.2 Schematic of SOHH under in-plane impact load

层级蜂窝的相对密度为：

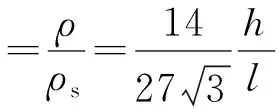
(1)

式中：ρ为层级蜂窝的密度；ρs为基体材料的密度；ρ*为层级蜂窝的相对密度。

1.2 模型验证

为了验证有限元计算的稳定性与可靠性，对网格尺寸敏感性进行了计算对比，网格尺寸确定为0.5 mm×0.5 mm.图3给出了刚性板以v=14 m/s时面内冲击普通蜂窝不同时刻的变形模式，并与RUAN[12]的计算结果进行了对比。从图中可以看到，本文的计算结果与文献[12]中传统正六边形蜂窝面内变形模式基本吻合，其结果证明了有限元模型的有效性与可靠性。

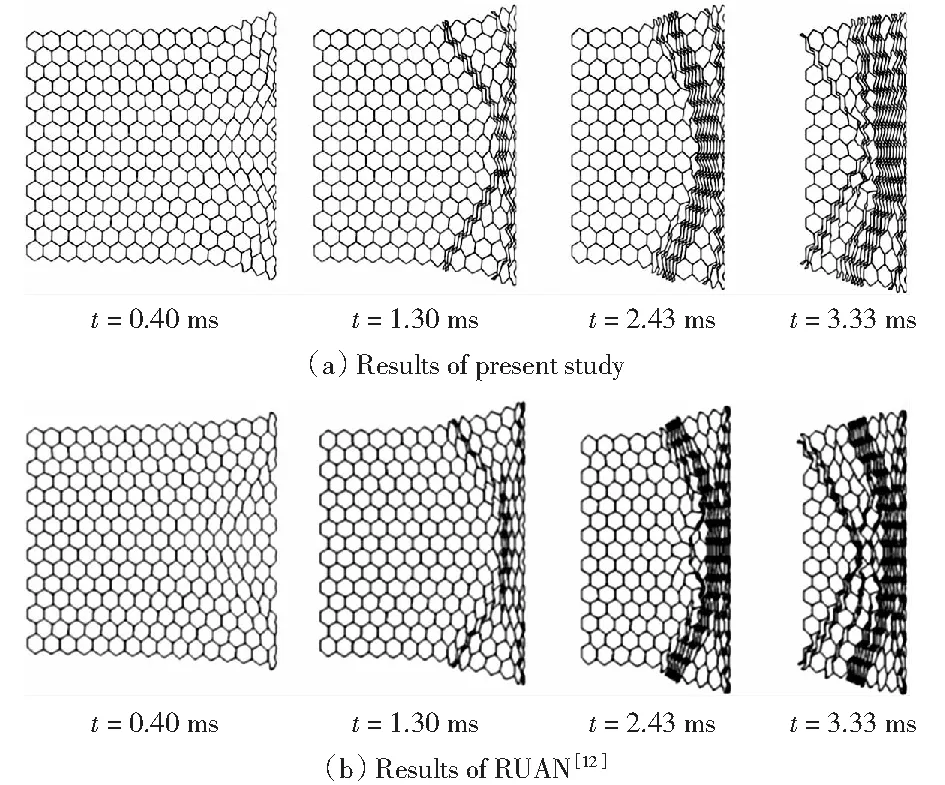
图3 六边形蜂窝沿面内压缩变形模式图Fig.3 In-plane compression modes of hexagonal honeycomb

2 变形模式

RUAN[12]通过数值仿真的方法研究了普通蜂窝在面内冲击载荷下的变形模式，研究表明在不同的冲击速度下，普通蜂窝在面内x方向的变形模式可分为准静态模式(X Mode)、过渡模式(V Mode)以及冲击模式(I Mode).本文对面内x方向和y方向不同冲击载荷下的二阶层级自相似六边形蜂窝的动力响应进行了研究，分析了冲击速度对层级蜂窝材料的变形模式的影响。

2.1 x方向的变形模式

不同冲击速度下层级蜂窝在x方向的变形模式，如图4-图6所示，其中层级蜂窝的二阶胞孔尺寸l=1.5 mm，二阶胞孔壁厚h=0.06 mm.当v=2 m/s时，支撑端附近胞元的局部变形产生了一个“X”形状的变形带(ε=0.14)，之后，变形不仅发生在变形带内，同时向附近的胞元拓展。当压缩应变达到0.36时，在冲击端出现了第二个“X”形状的变形带，并逐渐向支撑端拓展，直至一阶胞孔全部压溃。

v=2 m/s，l=1.5 mm，h=0.06 mm图4 层级蜂窝在x方向上的准静态模式(X Mode)变形Fig.4 Deformation of quasi-static mode (X Mode) of SOHH in the x direction

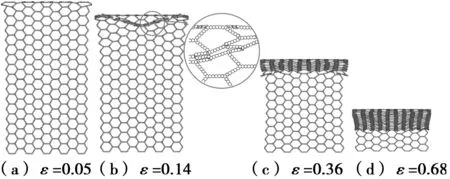
v=10 m/s，l=1.5 mm，h=0.06 mm图5 层级蜂窝在x方向上的过渡模式(V Mode)变形Fig.5 Deformation of transitional mode (V Mode) of SOHH in the x direction

当v=10 m/s时，在冲击端附近首先出现“V”形变形带(ε=0.14)，伴随着变形带内胞元的变形，变形带左右两侧各出现了一个由冲击端向支撑端逐层拓展的倾斜变形带，直至一阶胞孔全部压溃。

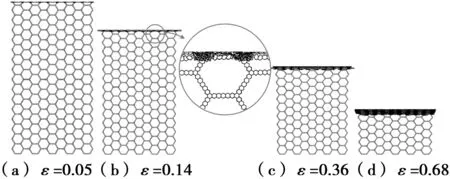
v=50 m/s，l=1.5 mm，h=0.06 mm图6 层级蜂窝在x方向上的冲击模式(I Mode)变形Fig.6 Deformation of impact mode (I Mode) of SOHH in the x direction

当v=50 m/s时，在整个冲击过程中变形区域完全集中在冲击端，形成了垂直于冲击方向的“I”形变形带(ε=0.14)，在整个压缩过程中没有出现明显的倾斜变形带。

2.2 变形模式分类图

通过以上对层级蜂窝的数值模拟结果的分析，表明冲击速度对层级蜂窝的变形模式具有显著影响。根据以上不同变形带的特征可将层级蜂窝在不同冲击速度下的变形模式相应的分为准静态模式，过渡模式与冲击模式。

将准静态模式转变为过渡模式的临界速度称为第一临界速度vc1[12]，将过渡模式转变为冲击模式的临界速度称为第二临界速度vc2[12]，在不同冲击速度下，对不同h/l的层级蜂窝进行数值模拟，对应的变形模式如图7.对数值模拟的结果进行拟合，最终得到式(2)的两个临界速度的经验公式：

(2)

由数值模拟的拟合结果式(2)可知，层级蜂窝的第一临界速度vc1和第二临界速度vc2与(h/l)1/2呈线性关系。

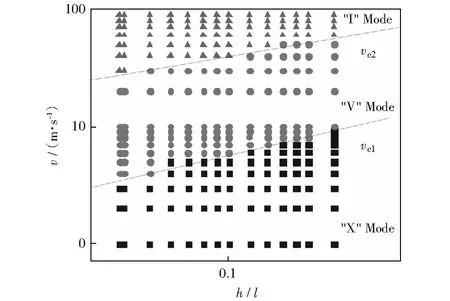
图7 层级蜂窝的变形模式分类图Fig.7 Deformation mode map of SOHH in terms of h/l and v

2.3 y方向的变形模式

层级蜂窝在y方向的变形模式，如图8-图10所示。当v=2 m/s时，最初，在支撑端处能够观察到一个“V”形的变形带(ε=0.14)，但是没有在x方向冲击时的倾斜V变形带明显。随着压缩方向位移的增加，靠近支撑端处的一阶胞孔开始发生折叠，形成垂直于加载方向的变形带(ε=0.36)，之后，发生折叠的区域从支撑端逐步拓展至冲击端，直至一阶胞孔完全压溃。冲击速度提高至20 m/s时，变形集中在冲击端附近，没有明显的倾斜带出现，形成垂直于加载方向的变形带(类似于x方向的冲击模式)。随着位移的增加，变形带通过渐进形式一层一层的由冲击端向支撑端扩展。相比冲击速度为2 m/s时的变形模式，该模式更加规则。进一步提高冲击速度(v=50 m/s)，变形越来越集中在冲击端，变形带仍呈现“I”形。

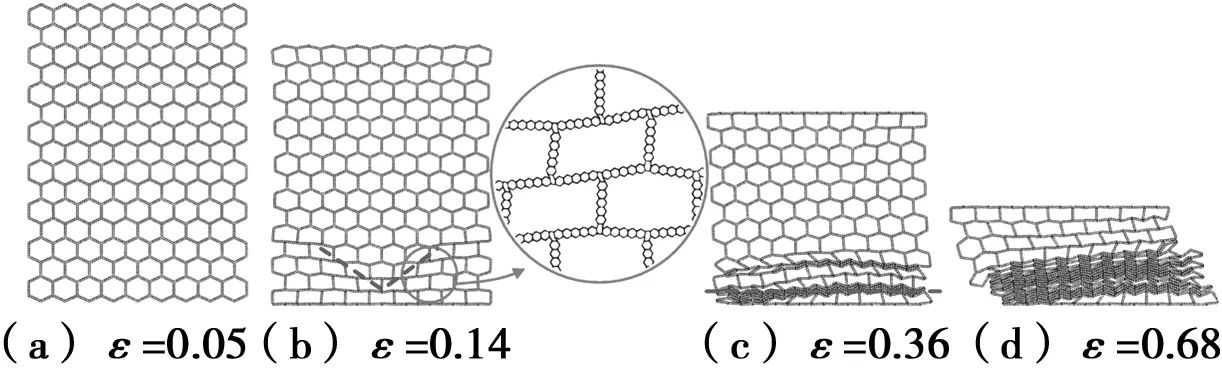
v=2 m/s，l=1.5 mm，h=0.06 mm图8 层级蜂窝在y方向上的准静态模式变形Fig.8 Deformation of quasi-static mode of SOHH in the y direction

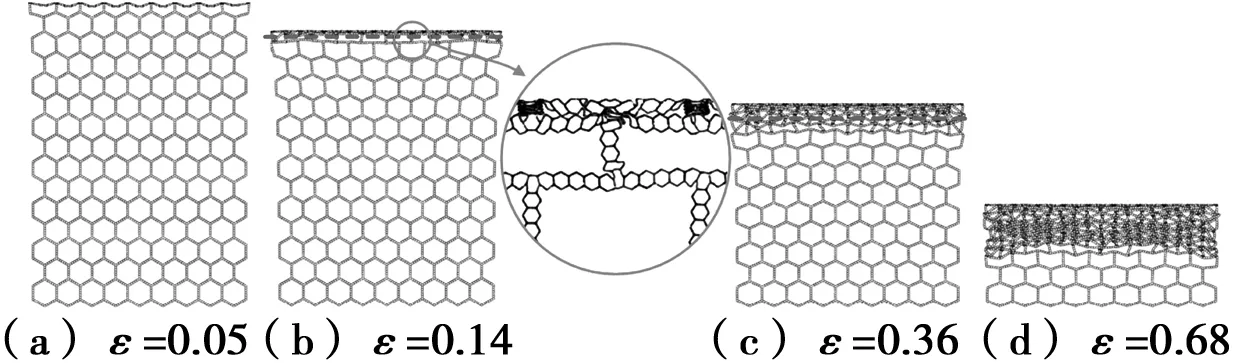
v=20 m/s，l=1.5 mm，h=0.06 mm图9 层级蜂窝在y方向上的冲击模式变形Fig.9 Deformation of impact mode of SOHH in the y direction

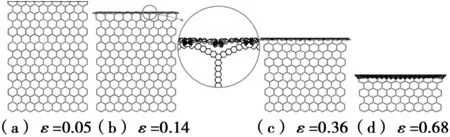
v=50 m/s，l=1.5 mm，h=0.06 mm图10 层级蜂窝在y方向上的冲击模式变形Fig.10 Deformation of impact mode of SOHH in the y direction

3 层级蜂窝的理论模型

3.1 层级蜂窝在x方向准静态模式下的理论模型

通过观察层级蜂窝准静态下的变形模式(图4)可知，层级蜂窝一阶胞孔的变形是由一阶胞孔角点附近的二阶胞孔的变形导致的。将一阶胞孔的孔壁视为连续均匀的梁[11]，只考虑宏观一阶胞孔孔壁的变形情况，建立如图11的理论模型。一阶胞孔的形状由正六边形变成了平行四边形，孔壁的变形为孔壁绕角点的旋转与孔壁长度的缩短，假定在孔壁的两端各有一个塑性铰(如图11绿色虚线中的黑点所示)。

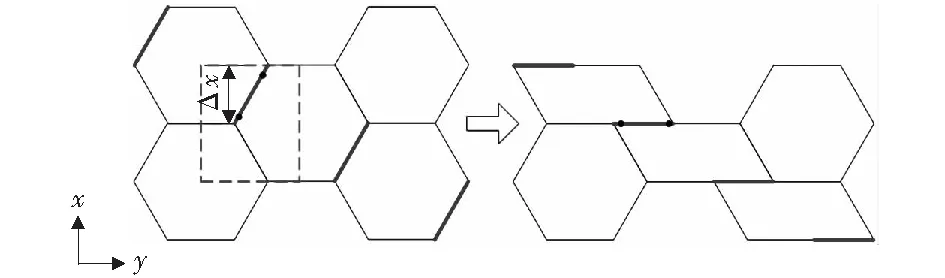
图11 层级蜂窝在x方向上准静态变形模式下的理论模型Fig.11 Analytical model of SOHH under quasi-static mode in the x direction

选取图11中的虚线框为计算单元，作用在单元上的外力功为

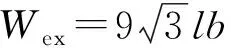
(3)

其中，σx为层级蜂窝在x方向上的平台应力，Δx=9l为x方向计算单元压缩的长度。

由塑性铰耗散的能量为

WM=2Mpθ.

(4)

其中，Mp=bl2σhex[11]为一阶孔壁的极限弯矩，θ=π/3为塑性铰的旋转角度；σhex为一阶孔壁的塑性压溃应力。由式(5)计算

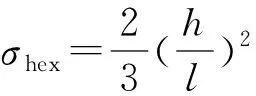
(5)

一阶胞孔孔壁的缩短所耗散的能量为

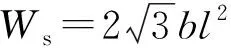
(6)

通过求解Wex=WM+Ws可得平台应力为

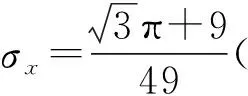
(7)

3.2 层级蜂窝在y方向准静态模式下的理论模型

通过观察层级蜂窝在y方向的准静态变形模式(图8)，通过与3.1中同样的方法，建立如图12所示的理论模型。根据数值模拟结果，假定每个孔壁具有两个塑性铰(图12中虚线框中的黑点)，黄色和蓝色的倾斜孔壁长度缩短，红色的竖直孔壁长度没有缩短。

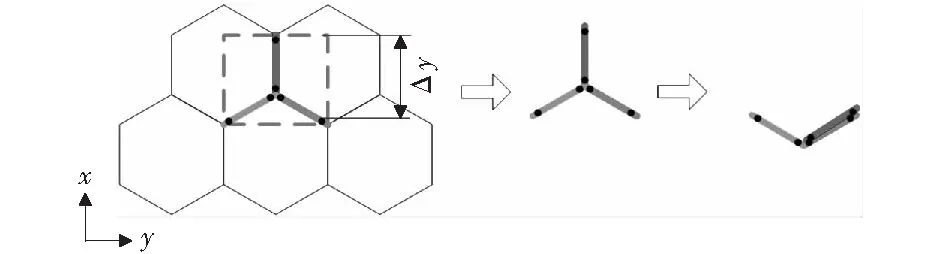
图12 层级蜂窝在y方向上准静态变形模式下的理论模型Fig.12 Analytical model of SOHH under quasi-static mode in the y direction

选取图12中的虚线框为计算单元，作用在单元上的外力功为

Wex=18σyblΔy.

(8)

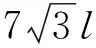
6个塑性铰所耗散的能量为

WM=6Mpθ.

(9)

其中，Mp=bl2σhex[11]为一阶孔壁的极限弯矩，θ=π/3为塑性铰的旋转角度。

2个倾斜的孔壁长度缩短所耗散的能量为

Ws=2Δsblσhex.

(10)

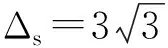
通过求解Wex=WM+Ws可得平台应力为

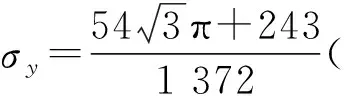
(11)

3.3 层级蜂窝在冲击模式下的理论模型

层级蜂窝在面内x，y方向冲击模式下的变形特征均为一层一层的渐进压溃，当胞元压溃并达到密实化应变时，它的速度从0增加到冲击速度v，外力的冲量为

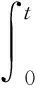
(12)

其中，σd为动态压溃应力；σqs为准静态模式下的平台应力(x方向为σx，y方向为σy)，在动态冲击时支撑端的应力近似的等于准静态模式的平台应力[13]；A是胞元的横截面积；t=εdH/v为胞元的速度从0增加到v的时间；εd为密实化应变[14]；H为胞元在压缩方向上压缩的长度。

胞元的动量变化量为

ΔP=AHρ*ρsv.

(13)

由动量守恒Pi=ΔP，可得动态平台应力为

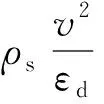
(14)

此处获得的动态平台应力的表达式与REID[15]的冲击波模型具有一样的形式。层级蜂窝在冲击模式下所表现出来一层一层的渐进压溃，所反映出的物理现象正是“冲击波效应”。

准静态变形模式下，不同相对密度的层级蜂窝在x，y方向的数值模拟得到的平台应力与理论平台应力如图13所示，从图中可知，在较大的相对密度范围内，理论模型与数值模拟的吻合程度较好。相对密度为1.15%的层级蜂窝在不同的冲击速度下平台应力如图14所示，从图中可以看出，在冲击速度较低时，由于层级结构的效应，面内x，y方向层级蜂窝的平台应力差别较大，但随着冲击速度的提高，两者之间的差别越来越小，这是因为冲击速度越高，惯性的影响越大，而惯性效应主要与密度和速度相关[16]。由式(14)可知，层级蜂窝的动态平台应力可分为准静态项σqs和惯性项ρ*ρsv2/εd，在本文中，由于层级蜂窝的相对密度是保持不变的，冲击速度变化时，对于准静态项没有影响，具有较大变化的为冲击速度的平方项v2，随着冲击速度的提高，惯性项所占的比重越来越大，因而随着冲击速度的提高，惯性的影响越来越大。

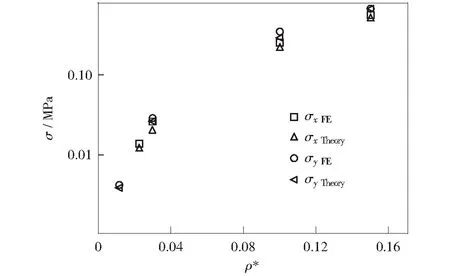
图13 不同相对密度的层级蜂窝在准静态模式下的平台应力Fig.13 Plateau stress of SOHH with different relative density under quasi-static mode

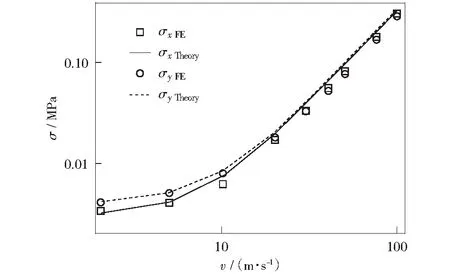
图14 相对密度为1.15%的层级蜂窝在不同冲击速度下的平台应力Fig.14 Plateau stress of SOHH with relative density 1.15% under different impact velocity

4 结论

本文提出了一种二阶层级自相似六边形蜂窝，并应用ABAQUS对其在面内冲击载荷下的响应进行了研究,并建立了x方向与y方向面内压缩理论模型。通过以上数值模拟与理论分析，得出以下结论：

1) 受到面内x方向冲击载荷时，层级蜂窝的变形模式表现为3种模式：准静态模式、过渡模式以及冲击模式。受到面内y方向冲击载荷时，层级蜂窝的变形模式表现为2种模式：准静态模式与冲击模式。

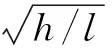
3) 将层级结构引入到普通蜂窝中形成层级蜂窝，面内压缩变形时，一阶胞孔的孔壁变形是孔壁绕角点的旋转与孔壁长度缩短两种变形机制的组合。通过能量平衡的方法建立的层级蜂窝面内压缩平台应力理论模型与数值模拟结果吻合较好。

：

[1] CHEN Q,PUGNO N M.Bio-mimetic mechanisms of natural hierarchical materials:a review[J].J Mech Behav Biomed Mater,2013,19:3-33.

[2] SCHAEDLER T A.Ultralight metallic microlattices[J].Science,2011,334(6058):962-965.

[3] PAPKA S D,KYRIAKIDES S.In-plane compressive response and crushing of honeycomb[J].Journal of the Mechanics & Physics of Solids,2015,42(10):1499-1532.

[4] GIBSON L J,ASHBY M F,CELLULAR SOLIDS.Structure and properties[M].Cambridge:Cambridge University Press,2014.

[5] GIBSON L J,ASHBY M F,HARLEY B A.Cellular materials in nature and medicine[M].Cambridge:Cambridge University Press,2010.

[6] TAYLOR C M.The effects of hierarchy on the in-plane elastic properties of honeycombs[J].International Journal of Solids & Structures,2011,48(9):1330-1339.

[8] LAKES R.Materials with structural hierarchy[J].Nature,1993,361(6412):511-515.

[9] YIN S,WU L,NUTT S.Stretch-bend-hybrid hierarchical composite pyramidal lattice cores[J].Composite Structures,2013,98(3):153-159.

[10] YIN S,WU L,NUTT S R.Compressive efficiency of stretch-stretch-hybrid hierarchical composite lattice cores[J].Materials & Design,2014,56(4):731-739.

[11] QIAO J,CHEN C.In-plane crushing of a hierarchical honeycomb[J].International Journal of Solids & Structures,2016,85/86:57-66.

[12] RUAN D.In-plane dynamic crushing of honeycombs——a finite element study[J].International Journal of Impact Engineering,2003,28(2):161-182.

[13] QIAO J,CHEN C Q.Analyses on the in-plane impact resistance of auxetic double arrowhead honeycombs[J].Journal of Applied Mechanics,2015,82(5):051007.

[14] LI Q M,MAGKIRIADIS I,HARRIGAN J J.Compressive strain at the onset of densification of cellular solids[J].Journal of Cellular Plastics,2006,42(5):371-392.

[15] REID S R,PENG C.Dynamic uniaxial crushing of wood[J].International Journal of Impact Engineering,1997,19(5/6):531-570.

[16] 胡玲玲，尤帆帆.铝蜂窝的动态力学性能及影响因素[J].爆炸与冲击,2012,32(1):23-28.

HU L L,YOU F F.Dynamic mechanical properties of aluminum honeycomb and its effect factors[J].Explosion and Shock Waves,2012,32(1):23-28.