基于变权与灰色关联决策的铁路线路方案评价模型研究

孙少伟

(中国铁路设计集团有限公司，天津 300142)

铁路选线是一项具有全局影响的总体性工作，选线质量将会直接影响工程、投资和运营等。为获取最优的线路方案，在选线设计阶段，有必要对各候选方案进行多方案比选与综合评价。而线路方案综合评价是一项复杂的决策问题，其影响因素中既包含线路长度、征地数量和投资费用等定量评价指标，又包括对生态环境的影响、吸引客流的能力等定性评价指标，很难用简单的方法进行处理。

传统铁路线路方案比选本质是追求工程费、运营费最少，并结合对各方案的环境影响、社会效应等定性因素的分析，得出最优方案[1]，一般只适用于定量指标的评价，对定性指标的评价仅局限于简单的描述，不能很好地将技术经济定量指标和社会环境影响定性指标综合起来评价[2]。此外，在对线路方案多项指标进行综合时，常常会通过权重来表征其在评价中的重要程度[3]。目前，指标权重的选取往往采用常权的形式(即权重大小是固定的)。但在实际问题中，对线路方案影响最大的往往是限制性因素，该类因素若不能满足最低要求，会对后期铁路的建设、运营产生不利影响。在常权评价中，限制性因素的消极影响很可能会被其他优势因素所掩盖，不能客观反映到评价结果中，从而造成决策失误。

为弥补铁路线路方案综合评价中的上述不足，以变权法和灰色关联决策法为基础，构建一种铁路线路方案综合评价模型。其基本思想是在权重选取的过程中引入变权方法，使评价指标的权重随其取值的变化而改变，避免方案的重大缺陷在评价时被其优势指标所掩盖。此外，将方案中的定性评价指标看作一个区间“灰数”，统一了不同类型的评价指标，并通过计算灰色关联度来完成对各方案的综合评价。最后结合工程案例，验证了其在铁路选线决策中的可行性和有效性。

1 变权理论

变权理论最早由汪培庄提出，强调指标权重随其取值的变化而改变，以弥补常权评价带来的偏差[4]。例如，在同时考虑可行性与必要性的评价问题中，假定其常权权重均为0.5，评价值f=0.5x1+0.5x2(x1为可行性，x2为必要性)。若方案甲：x1=0.1，x2=0.9；方案乙：x1=x2=0.5；则有f1=f2=0.5。也就是说常权评价下甲乙方案同样好，但这与实际情况不符，在评价时，还需要考虑指标的均衡性，必要但不可行的方案不会被采用。

1.1 变权性质

设X=(x1，…，xn)表示评价指标状态向量，变权理论有如下两个重要性质[5]。

(1)性质1

一组变权是指n个映射ωj(j=1，2，…，n)：[0，1]n→[0，1]，(x1，…xn)→ωj(x1，…，xn)，其应满足如下属性。

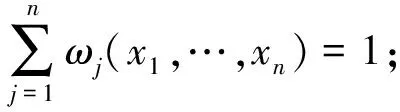
②连续性：ωj(x1，…，xn)(j=1，2，…，n)，每个变元连续；

③单调性：ωj(x1，…，xn)(j=1，2，…，n)，变元xj单调变化。

(2)性质2

记W(X)=(ω1(X)，…，ωn(X))为一组n维变权向量，构造映射S:[0，1]n→[0，1]n，X→S(X)=(S1(X)，…，Sn(X))，如果S(X)满足以下公理：

①xi≥xj→Si(X)≤Sj(X)；

②Sj(X)对每个变元连续(j=1，2，…，n)；

③对任何常权向量W=(ω1，…，ωn)，满足性质1中的条件①、②、③，则有

(1)

S(X)被称作惩罚型状态变权向量。W·S(X)=(ω1S1(X)，…，ωnSn(X))被称为Hardarmard乘积。可以看出，性质2中条件①是一个带有惩罚性质的条件，即当评价指标值减小时，其权重会相应增大，从而达到对该指标进行惩罚的效果。

1.2 状态变权向量

由上述变权理论性质可知，变权实现的核心是构造合适的状态变权向量S(X)。目前，已有和型、积型与指数型等多种状态变权向量类型[6]。其中，指数型状态变权向量因其使用简单、构造科学等特点，被广泛应用在物流分配、山区道路安全评价、水质评估等领域，并取得了较好的效果[7-9]。

指数型状态变权向量S(Xi)=(S1(X1)，…，Sn(Xn))的基本形式为

(2)

其中α称为惩罚(激励)水平，随着α的变化，变权效果也会不同：α<0时，函数为惩罚型变权，且α值越小，惩罚效果越好；α>0时，函数为激励型变权，且α值越大，激励效果越好；α=0时，变权评价即为常权评价。U在惩罚型变权下被称为否定水平，表示当评价指标值不大于U时，就会对该指标进行变权，通过增大其权重以达到惩罚的效果[10]。

2 灰色关联理论

灰色关联法是灰色系统理论中的一种分析方法，主要用于定量研究系统内多因素之间的复杂关系，在经济和社会生活中有着广泛的应用[11]。灰色关联法的主要原理是通过数列间曲线几何形态的相似程度来表征其联系的紧密程度，并将其用灰色关联度来量化，曲线愈接近，相应数列间的灰色关联度就愈大，反之则愈小[12]。在灰色关联理论中，灰色关联系数和灰色关联度的计算是最为重要的两个公式。

2.1 灰色关联系数

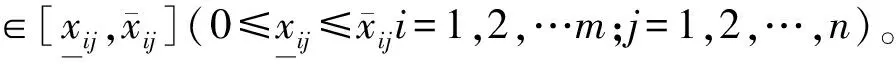
(3)

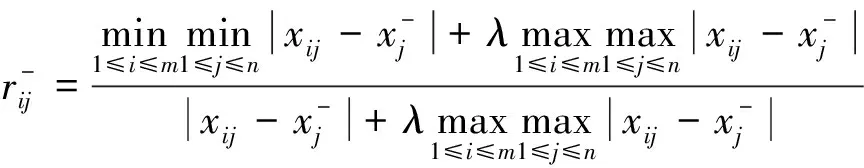
(4)

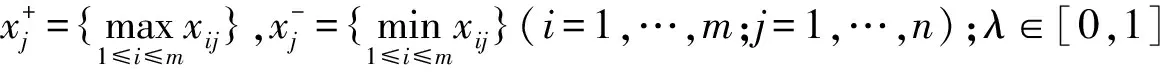
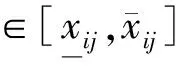
(5)

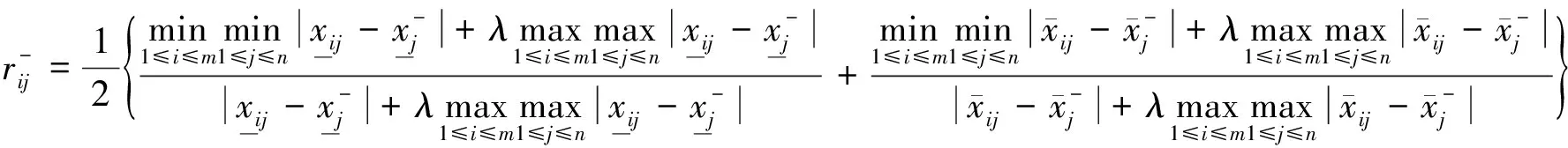
(6)

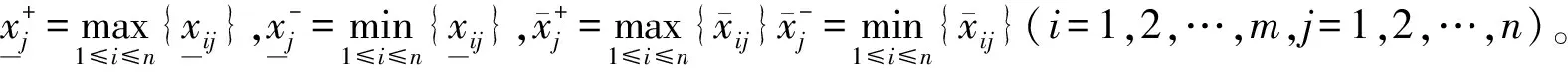
2.2 灰色关联度

在灰色关联系数的基础上，赋予每个评价指标相应的权重ωj(j=1，2，…，n)并综合求和，得到方案Ai关于最优方案A+的灰色关联度G(x+(⊗)，xi(⊗))和关于最差方案A-的灰色关联度G(x-(⊗)，xi(⊗))，其计算公式为

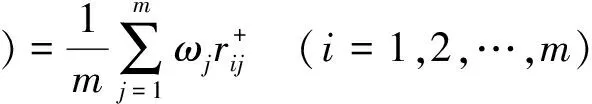
(7)

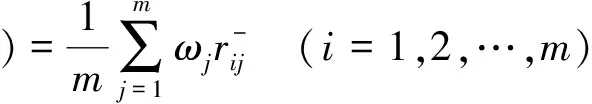
(8)

灰色关联决策就是通过灰色关联度来评价方案，从而完成对方案的优劣排序工作。文献[13]提出只考虑评价方案与最优方案间关系的最大关联度法和只考虑评价方案与最差方案间关系的最小关联度法均存在明显缺陷，其评价结果往往不够科学合理。而综合关联度法认为与最优方案灰色关联度最大、同时与最差方案灰色关联度最小的方案才是最佳方案。这种决策方法综合了两者的优势，还可以根据决策问题的实际情况和决策者的偏好选择不同的综合函数，使用起来十分灵活。

设方案Ai关于最优方案A+和最差方案A-灰色关联度的权重分别为β1、β2(β1+β2=1)，则方案Ai的综合灰色关联度为

G(xi(⊗))=β1G(x+(⊗)，xi(⊗))+

β2[1-G(x-(⊗)，xi(⊗))]

(9)

3 评价模型构建

通过整合变权法和灰色关联决策方法的优势，构造基于变权与灰色关联决策的评价模型，其步骤如下。

(1)构造决策矩阵(Step1)

根据铁路实际情况，确定参与比选的线路方案和评价指标，并将指标评价值数据构造成决策矩阵A

对于定性评价指标，选取与评价值对应的灰色区间数作为其取值，对应关系如表1所示。

表1 定性评价指标值与灰色区间数对应关系

(2)数据标准化处理(Step2)

线路方案评价指标值的单位、数量级以及对结果的作用方向各不相同，不能直接用来比较和计算，在使用前需先将数据进行标准化处理，构造出标准化决策矩阵X=(xij)m×n。本模型中决策矩阵的标准化采用灰色极差变换的方法来进行。

对定量指标评价值aij，灰色极差标准化公式为

效益型指标：

成本型指标：

(10)

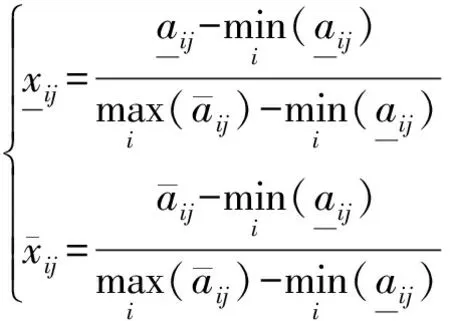
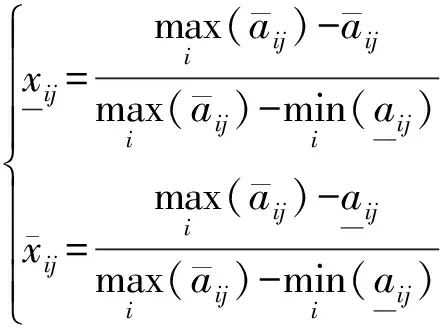
(11)

经过上述处理后，可获得标准化的数据，其值均处于[0，1]区间，且数值越大，其评价指标越优。

(3)确定最优和最差方案(Step3)

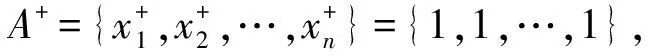
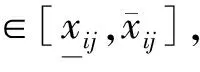
(4)计算灰色关联系数(Step 4)

定量评价指标灰色关联系数的计算可采用灰色关联系数计算公式(3)和公式(4)来完成；而定性评价指标灰色关联系数的计算，则需按灰色区间关联系数计算公式(5)和公式(6)来进行(分辨系数均取λ=0.5)。

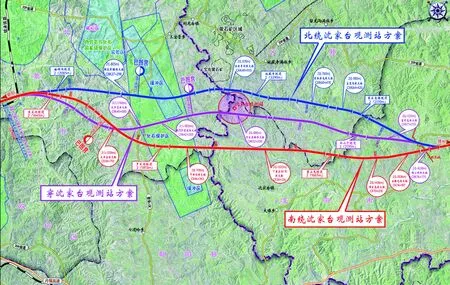
图1 沈家台观测站比较方案示意

(5)确定变权权重向量(Step 5)

变权需要在常权的基础上进行，常权的计算采用文献[14]提供的AHP法，通过比较指标间的相对重要程度得到常权权重向量W。在此基础上，采用惩罚性指数型变权形式进行变权。借鉴已有研究成果[15]，否定水平U=0.8，惩罚系数α=-0.5。

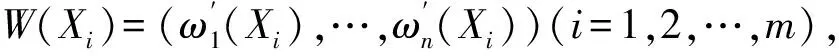
(6)计算变权权重下的灰色关联度(Step 6)

综合考虑各方案的灰色关联系数及其变权权重向量，利用式(7)和式(8)，即可计算得到方案Ai关于最优、最差方案的灰色关联度G(x+()，xi())、G(x-()，xi())。为使评价结果更加科学合理，选用综合关联度法将两个关联度进行综合。权重系数取β1=β2=0.5，最终得到各方案的综合关联度G(xi())，有

G(xi(⊗))=0.5×G(x+(⊗)，xi(⊗))+

0.5×[1-G(x-(⊗)，xi(⊗))]

(12)

4 实例分析

为更好地说明基于变权和灰色关联决策评价模型在铁路线路方案比选时的使用效果，选取京沈-盘营客专联络线局部线路方案，使用该评价模型对各候选方案进行综合评价，验证该方法的有效性。

锦州地震台沈家台观测站位于线路的航空线上，影响方案的走向。针对沈家台观测站的处理，主要研究了南绕沈家台观测站方案(方案Ⅰ)、穿沈家台观测站方案(方案Ⅱ)和北绕沈家台观测站方案(方案Ⅲ)，方案比较范围为CK21+200-CK84+000，方案示意如图1所示。

从工程、经济、环境和社会4个宏观层面，选取C1线路长度、C2桥隧长度等10个评价指标，对3个候选方案进行评价比选，各方案评价指标取值情况见表2。

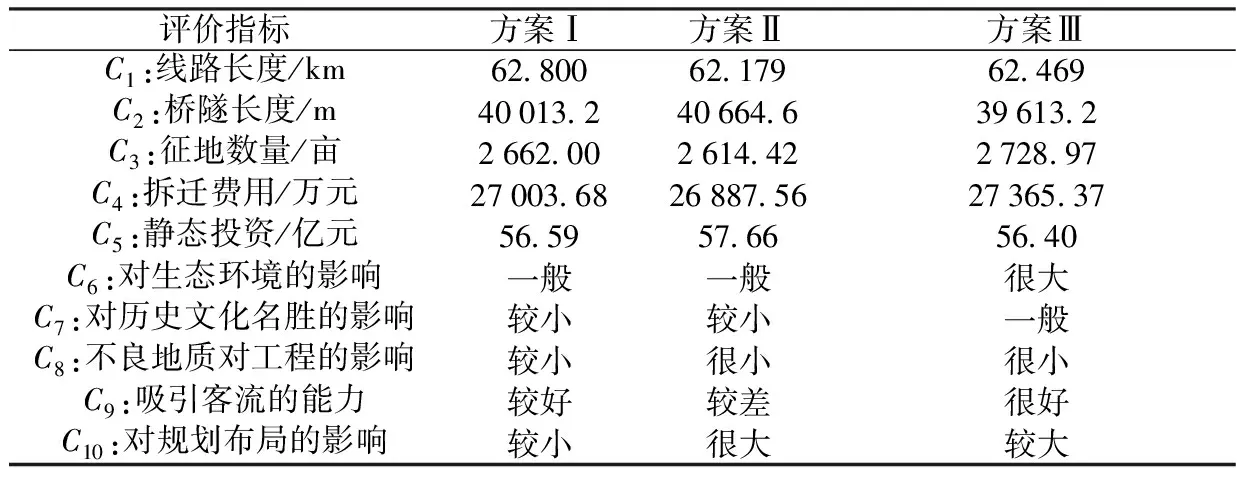
表2 各候选方案评价指标取值

将表2中的评价指标取值数据构造成决策矩阵A，其中指标C6-C10的取值按表1中对应关系用灰色区间数表示。利用灰色极差变换公式(10)、公式(11)对决策矩阵中的数据进行标准化处理，使其均处于[0，1]区间内，得到标准化决策矩阵X

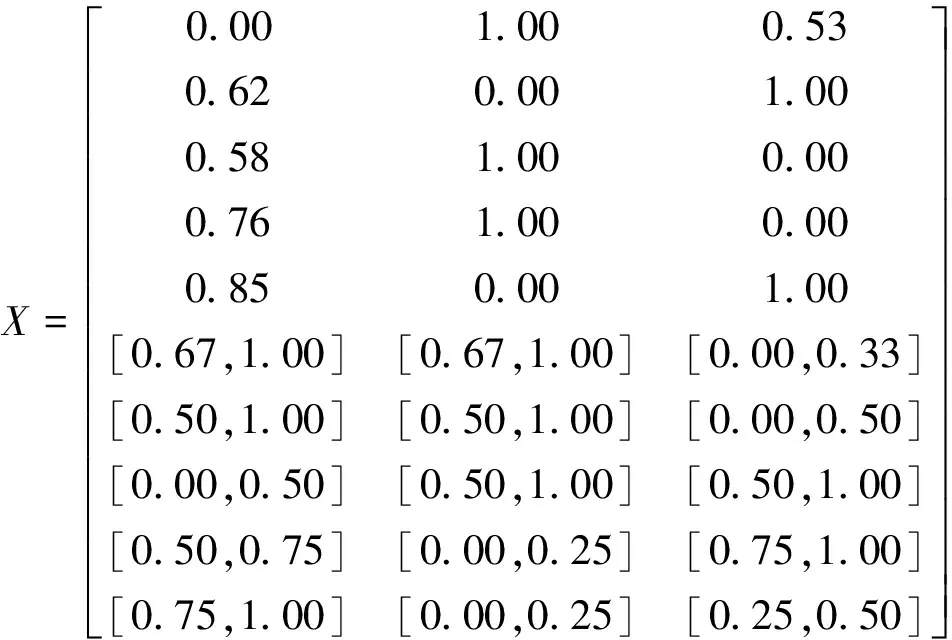
根据3.3节中的方法确定最优方案A+和最差方案A-。采用式(3)～式(6)分别计算评价指标C1～C10的灰色关联系数，得到各方案的灰色关联系数矩阵R+、R-。

利用AHP法计算得到各评价指标在常权下的权重向量

W={ω1，…，ω10}={0.143，0.007，0.112，0.118，0.152，0.008，0.085，0.08，0.08，0.08}。

在常权基础上，采用式(2)的变权形式对各方案评价指标进行变权，得到各方案的变权向量W(Xi)

综合灰色关联系数矩阵R+、R-和变权权重向量W(Xi)，求得各方案关于最优方案和最差方案的灰色关联度，再利用式(12)将两关联度综合起来，最终得到各方案在变权权重下的综合灰色关联度。为方便进行对比研究，还分别求得了常权情况下各方案的综合灰色关联度，其评价结果见表3。

表3 基于常权和变权方法的各方案综合灰色关联度

与常权情况相比，3个方案的综合灰色关联度在经过变权后均有所减小。这是因为在变权过程中，对方案中的劣势指标进行了惩罚性变权，加大了其权重，而变相地减小了优势指标的权重，从而造成了各方案综合灰色关联度的减小。可见，变权法的最终效果就是将方案中存在的劣势与缺陷进行放大，较为适于对风险十分敏感的铁路线路方案的决策工作。

此外，方案评价结果的排序在变权之后也发生了变化，常权下最优的方案Ⅱ在变权后成为了次优方案，而方案Ⅰ成为了变权后的最优方案。这是因为方案Ⅱ中各评价指标值极不均衡，尽管采用穿越观测站的形式通过，其线路长度、征地数量等指标是三个方案中最好的。但该方案受安全保护区控制，其车站只能选在巴图营乡东南7 km左右的位置，对附近旅客出行造成不便；且线路自沈家台观测站南侧650 m通过，不满足相关规范要求。

反观方案Ⅰ，虽然评价指标中最优项较少，但没有明显的劣势项，指标间取值比较均衡且评价指标值基本处于中等偏上水平，既满足穿越朝阳市化石保护区的规范要求，又满足沈家台观测站的距离要求。

5 结论

铁路线路方案评价指标种类众多，既有定性指标又有定量指标，若各指标权重大小固定不变，易产生决策偏差，构建基于变权和灰色关联决策的评价模型，并使用该模型对实际工程线路方案进行评价比选。结果表明：(1)所构建的模型能够很好地将定性指标和定量指标进行统一量化；(2)通过对方案的劣势指标进行惩罚性变权，指标间取值较为均衡的方案在比选中胜出，使最终评价结果更加科学合理。

[1] 吴小萍，陈秀方.线路方案灰色优选模型及其应用研究[J].系统工程理论与实践，2002(7):101-105

[2] 李远富，薛波，邓域才.铁路选线设计方案多目标决策模糊优选模型及其应用研究[J].西南交通大学学报，2000(5):465-470

[3] 罗圆，姚令侃，魏永幸.铁路选线方案比选指标权重确定及灵敏度分析[J].重庆交通大学学报(自然科学版)，2015，34(6):73-78

[4] 李洪兴.因素空间理论与知识表示的数学框架(Ⅷ)—变权综合原理[J].模糊系统与数学，1995(3):1-9

[5] 李德清，李洪兴.状态变权向量的性质与构造[J].北京师范大学学报(自然科学版)，2002，38(4):455-461

[6] 李德清，郝飞龙.状态变权向量的变权效果[J].系统工程理论与实践，2009，29(6):127-131

[7] 周晓，张锦，张菲，等.基于变权的多目标物流网络货流分配方法[J].西南交通大学学报，2012(1):151-157

[8] 游克思，孙璐，顾文钧.变权综合评价法在山区道路安全评价中应用[J].系统工程，2010，28(5):85-88

[9] Li Bing， Yang Guishan， Wan Rongrong， Zhang Lu， Zhang Yanhui， Dai Xue. Using Fuzzy Theory and Variable Weights for Water Quality Evaluation in Poyang Lake， China[J]. Chinese Geographical Science， 2017，27(1):39-51

[10] 杨宝臣，陈跃.基于变权和TOPSIS方法的灰色关联决策模型[J].系统工程，2011，29(6):106-112

[11] 梅晓玲.基于灰色关联与投影算法的铁路货运量影响因素分析[J].四川理工学院学报(自然科学版)，2015，28(5):85-88

[12] 刘思峰，谢乃明.灰色系统理论及其应用[M].北京：科学出版社，2008

[13] 罗党，刘思峰.灰色关联决策方法研究[J].中国管理科学，2005(1):102-107

[14] 赵红星.层次分析法在铁路工程评标指标权重中的应用[J].铁道工程学报，2012，29(10):120-123

[15] 聂茂林.供应链合作伙伴选择的层次变权多因素决策[J]. 系统工程理论与实践，2006(3):25-32