平均间隙法的一种改进算法

滕焕乐 聂虎啸 刘成龙

(1.中铁第四勘察设计院集团有限公司，湖北武汉 430063；2.中国铁路设计集团有限公司，天津 300142；3.西南交通大学地球科学与环境工程学院，四川成都 610031)

变形监测网稳定性分析的基准点一般应远离变形体且地质情况稳定[1，4]，这样可以保证每次测量都能得到监测点相对于同一个位置基准的位移量。理论上，根据基准点提供的固定位置基准解算监测点的变形量是可靠的，然而由于多种原因，基准点也有可能发生位移，如果仍然采用发生位移的基准点进行测量与平差，则不能准确地反映形变发生的实际情况，从而得出错误的变形分析结果和结论。因此，在变形监测网平差计算之前，对变形监测基准点进行稳定性分析至关重要。

目前，对变形监测网进行稳定性分析的主要方法有t检验法、平均间隙法等。t检验法适用于图形简单、点数较少的监测网[2]。平均间隙法的应用则更广，常用于监测网稳定性的显著性检验。

1 平均间隙法的传统算法

1.1 整体检验

平均间隙法是变形监测网稳定性分析的一种常用方法。首先通过整体检验，对变形监测网的稳定情况进行判断，若判断结果显示网中无动点，则稳定性分析结束；反之，则应通过后续的不稳定点搜索找出网中的动点。

1.2 不稳定点搜索

若整体检验没有通过，则意味着网中存在不稳定点，需要找出这些不稳定点。首先将网中所有点分为稳定点F组和不稳定点M组，同时将坐标间隙ΔX以及间隙的权阵PΔX分组，具体分组方法如下[6]

(1)

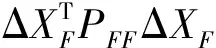
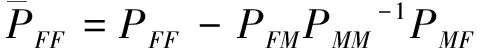
(2)

由此获得

(3)

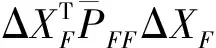
令

(4)

则F组点稳定性检验的统计量为

(5)

式中，μ2为两期观测的联合单位权方差，其自由度为f。

若F1F(fF，f)，则F组中含有不稳定点。

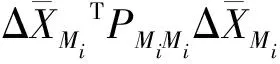
1.3 传统算法的不足

(1)过程复杂计算量大

在进行过一次搜索后，之后的每次搜索计算，需要提取至少两个点的间隙权阵信息，该项工作较提取一个点的间隙权阵复杂，且计算量较大，影响稳定性分析的效率。

(2)数据重复使用

传统做法是将已搜索出的不稳定点再次纳入不稳定点组，进行其他不稳定点的搜索，数据重复使用。

(3)循环性不强编程计算较为复杂

平均间隙法的传统算法循环性不强，按照其算法原理进行编程计算较为复杂，影响算法效率。

2 平均间隙法的改进算法

2.1 不稳定点的搜索

利用传统算法进行第一次搜索后，确定监测网的t个点中第i点为可能的不稳定点，改进后的方法是不再将i点纳入第二次及之后搜索的不稳定点组中，而是剔除i点，将剩余的t-1个点视为整体。依次将t-1个点作为不稳定点组，计算其不稳定性指标，将其中最大的点视为不稳定点，然后再检验其余点所构成网的图形一致性。若第二次搜索后其余点的图形一致性通过检验，则稳定性检验结束。若未通过检验，则需要进行第三次甚至更多次的搜索。第三次及之后的搜索与第二次搜索一样，亦不考虑已搜索出的不稳定点，其搜索过程与传统算法的第一次搜索一致，每搜索出一个动点后就对剩余的点进行图形一致性的检验。重复上述过程，直到剩余的点均稳定为止。

2.2 改进算法的优势

从上述改进算法中可以看出，改进后的算法较传统算法简单、计算量小、循环性强，有利于提高编程和计算的效率，更适用于监测网的稳定性分析。

3 设计与算例分析

共选取了8个点，构成一个高铁的沉降监测网。网中有3个基准点(BM1、BM2、BM3)和5个监测点(1～5号点)，对该网进行两个周期的沉降监测。在第二期测量时，将基准点中的BM3点抬升2 mm左右，将监测点中的3号点下降3 mm左右，以达到验证稳定性分析结果的目的。具体网形设计如图1所示。

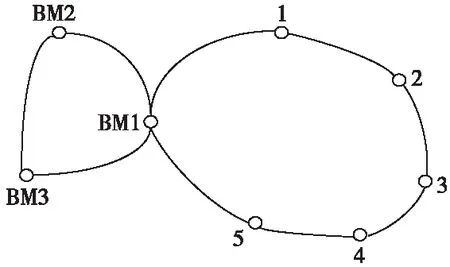
图1 计算实验设计的沉降监测网

3.1 第一部分实验

仿真设计监测网两期观测资料如表1所示。

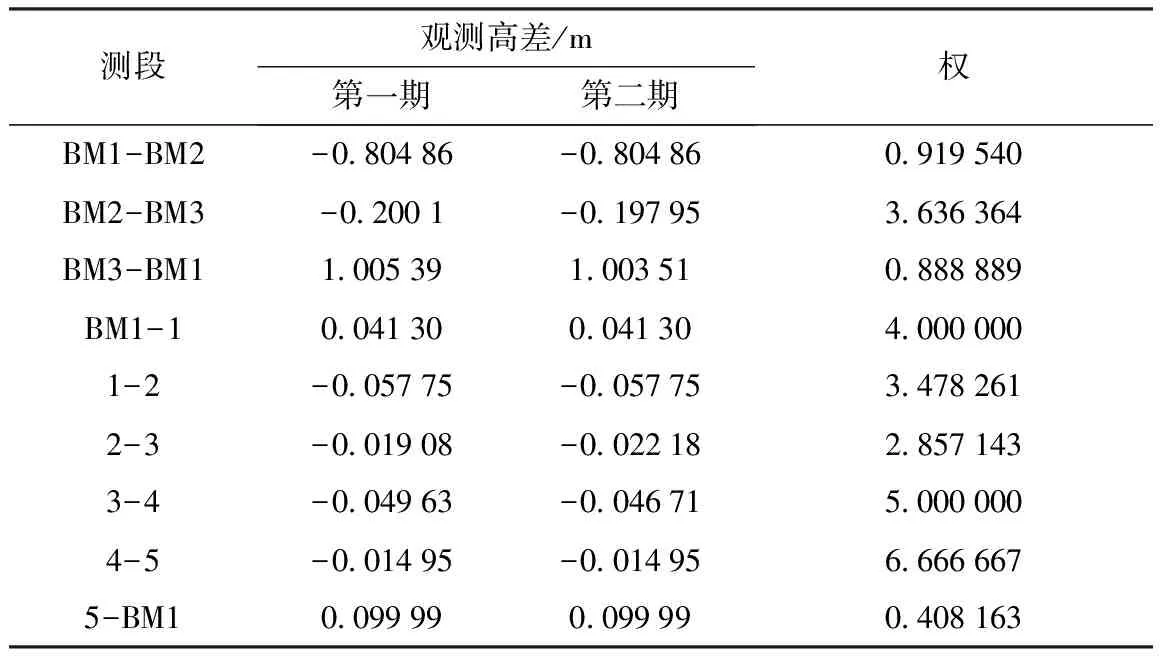
表1 沉降监测网的两期观测资料

(1)平均间隙法传统算法

两期监测网经自由网平差后，结果如表2所示。

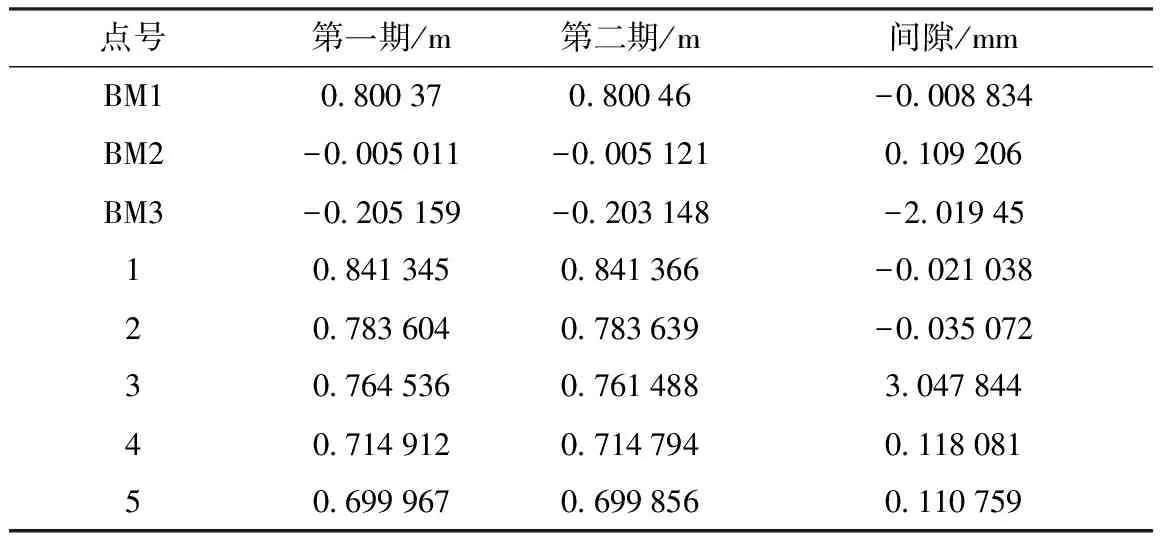
表2 两期监测网自由网平差结果

①整体检验

根据两周期观测资料秩亏自由网平差结果，求得的间隙及其权阵如下

ΔX=(-0.008 834，0.109 206，-2.010 945，-0.021 038，-0.035 072,3.047 844,0.118 081,0.110 759)T

(6)

两期观测平差后，联合方差估值为

(7)

假设两次观测监测点没有变动，则可计算联合方差估值

(8)

构造F检验统计量

(9)

检验没有通过，故应认为网中存在不稳定点。

②不稳定点的搜索

分别将网中的点看做动点，计算8个点的图形不一致性指标，结果如表3所示。

表3 各点图形不一致性指标

注：若点的图形不一致性指标<10-5，取0。

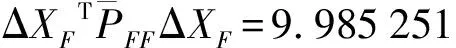
对剩余的点重新构成统计量，进行稳定性整体检验

(10)

F检验没有通过，需继续进行不稳定点搜索。将剩余的7个点与不稳定点3组成不稳定点组，计算7个不稳定点组的图形不一致性指标，计算结果见表4。

经比较发现，BM3点和3号点构成的不稳定点组的图形不一致性指标最大，故怀疑BM3点发生变动。同时剔除3号点和BM3点，计算剩余点的图形一致性指标，并做整体检验

表4 各点组图形不一致性指标

(11)

剩余点通过检验，由此认为网中除了3号点和BM3点外，其余的点均为稳定点。

③稳定性分析结果

网中3号点和BM3点发生变动，其余点均未发生变动，与实验设计结果一致。

(2)平均间隙法的改进算法

①不稳定点搜索

在确定3号点为不稳定后，将剩余7个点重复第一次搜索过程。过程如下：

将剩余7个点依次看做动点，作为不稳定点组，分别计算7个点图形不一致性指标，结果如表5所示。

表5 各点的图形不一致性指标

经比较发现，BM3点的图形不一致性指标最大，故怀疑BM3点发生变动。剔除BM3点，对剩余6个点做整体检验

(12)

剩余6个点通过检验，由此认为网中除了3号点和BM3点，其余的点均未发生变动。

②稳定性分析结果

经过检验，认为网中3号点和BM3点发生变动，其余点均未发生变动，与实验设计结果一致。

(3)两种方法的稳定性分析结果比较

上述两种不同稳定性分析方法的检验结果均显示，整个沉降监测网中BM3点和3号点发生变动，与试验设计相符。

3.2 第二部分实验

(1)对基准点进行稳定性分析

根据两周期观测资料，首先对基准网进行秩亏自由网平差，求得各点间隙及其权阵

(13)

经整体检验，网中存在不稳定点。

分别将网中的点看做动点，计算3个点的图形不一致性指标，结果如表6所示。

表6 各基准点的图形不一致性指标

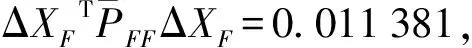
(14)

通过检验，由此认为，基准点中只有BM3点为不稳定点。

(2)对监测点进行经典自由网平差及稳定性分析

通过上述计算确定基准点中BM3点为不稳定点，剔除BM3点，将两次基准点秩亏自由网平差得到的BM1点高程的均值作为经典自由网平差的起算数据，对两期观测数据进行经典自由网平差。平差后，各监测点的间隙及其权阵如下

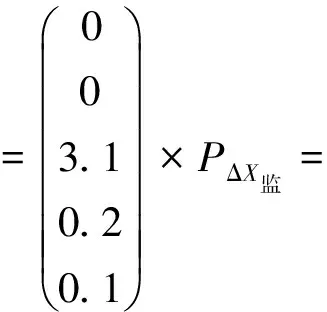
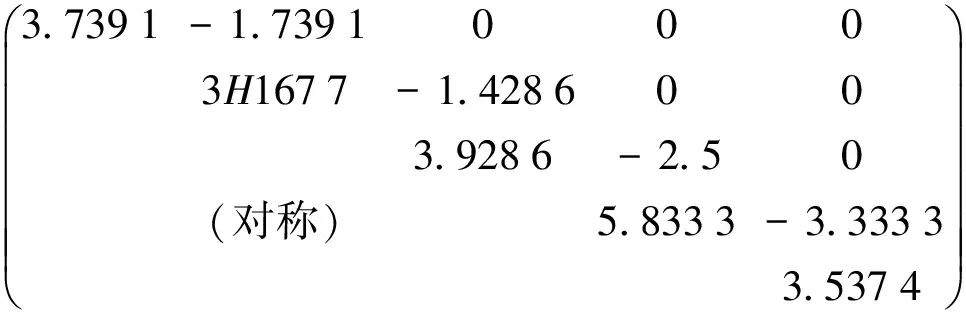
(15)

经整体检验，网中存在不稳定点。

分别将网中的点看做动点，计算5个点的图形不一致性指标，结果如表7所示。

表7 各监测点的图形不一致性指标

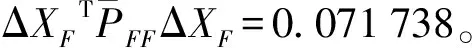
对剩余的点重新构成统计量，做整体检验

(16)

通过F检验，证明只有3号点不稳定。

(3)稳定性分析结果

结合上述(1)、(2)步的计算，检验出全网中BM3点和3号点为不稳定点，其余点均未发生变动，与试验设计一致。

4 结论

(1)无论是采用平均间隙法的传统算法，还是采用本文提出的改进算法，均可以对沉降监测网进行稳定性分析。改进算法的计算过程更为简单，条理更清晰。

(2)计算试验的第一部分中，将基准点与监测点一起进行稳定性分析，并且得到了与实验设计一致的结果，由此说明，平均间隙法可同时对基准点和监测点进行稳定性分析。

(3)计算试验的第二部分中，在对基准点进行稳定性分析后，利用稳定的基准点对监测点进行经典自由网平差，并利用平差结果进行监测点的稳定性分析，得到的结果与试验设计相符。由此说明，当监测网中有稳定的基准点时，可以对精测网进行经典自由网平差，再利用平均间隙法对监测网进行稳定性分析，算法更为简单。

[1] 杨学超，杨彩平.平均间隙法和单点检验在变形监测网中的应用[J].兰州交通大学学报，2011，30(6):30-32

[2] 韩易，黄腾，沈月千，等.基于改进平均间隙法的狭长区域平面控制网稳定性检验[J].水利与工程技术学报，2013(4):164-167

[3] 尹晖，杨睿，陈鹏云.监测网基准点稳定性检验方法与应用[J].武汉理工大学学报，2012，32(6):861-864

[4] 黄声享，尹晖，蒋征.变形监测数据处理[M].武汉:武汉大学出版社，2010

[5] 陶本藻.自由网平差与变形分析[M].北京:测绘出版社，1984

[6] 黄立人.用于相对稳定点组判别的QUAD法[J].大地测量与地球动力学，2002(2):10-15

[7] 滕松，张铎强，周照明，等.网形不一致的工程控制网稳定性分析[J].测绘工程，2009，18(2):59-62

[8] 陈刚，张军，等.地铁沉降监测网稳定性分析与探讨[J].测绘通报，2012(12):25-29

[9] 吴杰，余腾，潘庆林.工程控制网的稳定性研究[J].测绘科学，2011，36(5):31-33