地震作用下地下厂房混凝土衬砌结构稳定分析

王小威，陈俊涛，肖明，邓建



地震作用下地下厂房混凝土衬砌结构稳定分析

王小威1, 2，陈俊涛1, 2，肖明1, 2，邓建1, 2

(1. 武汉大学 水资源与水电工程科学国家重点实验室，湖北 武汉，430072；2. 武汉大学 水工岩石力学教育部重点实验室，湖北 武汉，430072)

针对混凝土循环荷载作用下的率相关性和疲劳损伤特性，提出考虑拉、剪损伤各向异性的混凝土动力本构模型，并推导出损伤变量动态演化方程；针对围岩与衬砌动力相互作用特点，提出考虑围岩与衬砌非连续变形的显式动力有限元积分方法；由此，构建地下厂房混凝土衬砌结构动力响应分析方法，并将该方法应用于映秀湾水电站地下厂房抗震稳定计算。衬砌结构各部位在地震下处于同步震动状态，其中衬砌顶拱应力和位移波动幅度较大；主厂房衬砌顶拱与边墙最大相对位移达到1.6 cm，说明主厂房发生了较为明显的结构变形；衬砌结构损伤区主要分布在顶拱处，其中拉裂损伤造成的损伤破坏较为严重；围岩对衬砌结构的约束作用有助于衬砌结构的抗震稳定性。应用上述方法所得的计算结果较为合理地反映了衬砌结构动力响应特征，可为地下厂房混凝土衬砌结构抗震设计提供参考。

地下厂房；混凝土衬砌；动力响应；拉、剪损伤各向异性；动力本构；非连续变形；显式动力有限元

中国西南高地震烈区分布着多座大型水电站，这些水电站地下厂房在地震作用下的稳定性对水电站安全运行至关重要。人们对地下厂房动力响应进行了大量研究[1−4]，取得了丰富的研究成果，但是对厂房衬砌结构动力响应特征研究较少。张雨霆等[5−6]的研究表明，地下厂房衬砌结构是地下厂房抗震设计的重要组成部分，因此研究其地震动力响应具有重要意义。地下厂房衬砌结构地震动力响应分析主要包括2个方面的内容：一是衬砌混凝土材料的动态响应分析，二是地震作用下洞室围岩与衬砌相互作用分析。混凝土材料的动力本构模型是地下厂房衬砌结构动力分析的基础，许多研究者基于室内实验或理论推导建立了各种混凝土动态本构模型以研究混凝土材料的动力响应规律，主要包括弹塑性动力本构模型[7−9]、非线性弹性动力本构模型[10−11]、黏塑性动力本构模型[12−13]和动力损伤本构模型[14−16]，其中动力损伤本构模型应用最为广泛。由于自身结构特征，混凝土在加载前其内部就分布着微小缺陷，在地震循环荷载作用下，这些缺陷不断发展、贯通。由此可见，混凝土的破坏过程是损伤累积发展的过程，要全面了解混凝土的动力响应特征就需要研究其内部缺陷的演化过程[17]，这也使得损伤理论被广泛应用于混凝土的动态响应分析[18−19]。关于围岩与衬砌相互作用的研究，人们展开了大量工作。朱维申[20]建立了黏弹塑性岩体中围岩与衬砌共同作用时一个轴对称问题的解析表达式；肖明等[21]采用弹塑性有限元研究了洞室开挖变形对衬砌作用的影响；CHEN等[22]采用三维非线性薄层单元研究了围岩与衬砌相互作用。可以看出，这些研究主要针对静力情况，对地震荷载作用下围岩与衬砌的动响应问题关注较少。事实上，围岩与衬砌作为一个共同作用体系，其在地震荷载作用下的响应与静力条件下的有很大不同；静力条件下可认为围岩与衬砌变形协调，两者在接触面处位移是连续的，但是在动力条件下，由于两者材料的差异性，加上接触面对地震波传播的影响，两者在接触面处的位移是不连续的。因此，在构建围岩与衬砌动力条件下的相互作用模型时，需要考虑到围岩与衬砌在地震荷载作用下的非连续变形。基于上述思路，本文作者建立混凝土拉、剪损伤各向异性动力本构模型，推导出损伤变量动态演化方程，提出考虑围岩与衬砌非连续变形的显式动力有限元积分方法，并在此基础上构建地下厂房混凝土衬砌结构动力响应分析方法。将该方法应用到映秀湾水电站地下厂房动力计算中，研究地下厂房混凝土衬砌结构震损演化过程，为地下厂房衬砌结构抗震设计提供参考。

1 混凝土衬砌动力损伤本构模型

前期研究表明[23−26]，在动力循环荷载作用下，混凝土材料表现出明显的率相关性和疲劳损伤特性，其率相关性主要体现在物理力学参数随应变率的提高而增加。混凝土是一种非均质的多相材料，在地震循环荷载作用下，其内部固有的微裂隙和微空洞不断地扩展和累积，最终形成宏观上的损伤破坏。在这个过程中，混凝土材料的强度和刚度不断退化，表现出疲劳损伤特性。基于以上事实可知，要构建混凝土衬砌动力本构模型，则需要包含这2个方面特征。因此，本文作者在损伤理论的基础上，建立考虑应变率效应的混凝土动力损伤本构模型。

1.1 基于拉、剪分离的混凝土动力损伤模型

混凝土动力损伤本构需要反映混凝土的率敏感性和损伤的产生与演化，其一般形式可以写为

对损伤变量描述的合理性很大程度上决定了损伤模型的准确性，目前工程计算采用的模型中，损伤变量形式主要为标量形式，其形式简单，便于理论推导和大规模数值计算。然而混凝土作为一种非均质材料，在荷载作用下，特别是在地震循环荷载作用下，其损伤演化是具有方向性的，因此损伤的度量应该采用张量的形式[17]。混凝土的损伤形态主要有受拉损伤和受剪损伤，2种损伤形态的产生机制各不相同，损伤对强度和刚度的影响也表现迥异。因此将动态损伤变量分为受拉和受剪2个部分[27]。

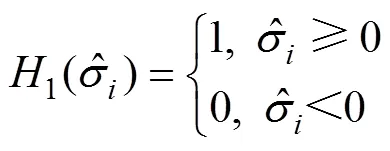
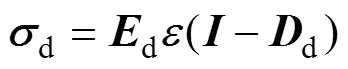
1.2 混凝土拉、剪损伤变量演化方程

由前面推导过程可知，要构建完整的混凝土动态损伤模型，还需要建立动力作用下混凝土拉、剪损伤变量演化方程。动力作用下的拉、剪损伤演化过程与静力作用下不同之处在于：动力损伤的演化过程不仅与应变有关，而且与应变率相关。因此，建立率相关的损伤演化方程是关键。

假设在三维复杂应力状态下，单元的受拉破坏满足最大拉应变法则。按照文献[28]中的方法，采用等效应变来表示三维应力状态下的最大拉应变，则受拉损伤变量演化方程可以表示为

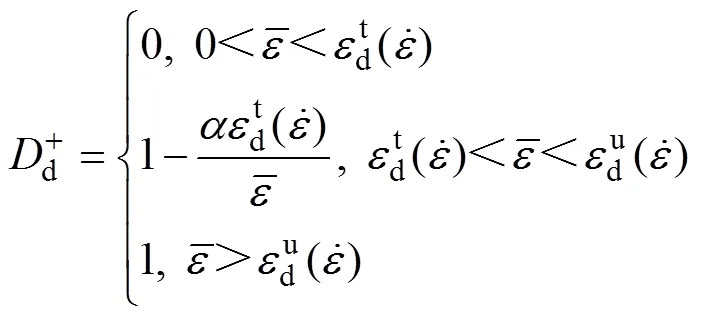
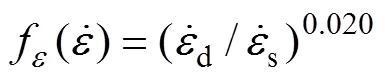
式(8)~(12)构成了完整的动力受拉损伤变量演化方程。类似地，三维应力状态下的剪切损伤变量演化方程可以表示为

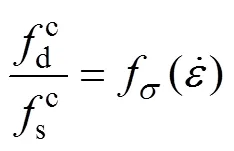
同理可知，式(13)~(16)构成了完整的动力剪切损伤变量演化方程。由以上分析可知，本文的动态受拉损伤变量与剪切损伤变量是直接在最大拉应变准则和Mohr-Coulomb准则的基础上，考虑应变率效应而得出的，形式简单，易于有限元计算。

2 围岩与衬砌非连续变形的动力分析方法

地下厂房可以看作是混凝土结构与围岩的联合体。混凝土衬砌与围岩在地震波作用下发生受迫振动，由于混凝土介质与岩石介质的差异性，加上围岩与衬砌间存在非连续接触面，围岩与衬砌对于地震动的响应存在明显差异。这种差异造成了衬砌与围岩非连续变形，即衬砌与围岩间存在相对位移差，由相对位移差引起的应力差则是围岩与衬砌间发生损伤破坏的主要原因。本文作者基于显式积分法，结合围岩与衬砌接触条件，建立围岩与衬砌非连续变形动力分析方法。

2.1 围岩与衬砌介质运动方程的时域显式积分方法

根据衬砌与围岩的有条件联合承载特征，可以将衬砌与围岩地震作用下的联合承载过程看作是混凝土衬砌与岩体这2种材料有条件单独承载过程的叠加。依据围岩与衬砌的动力有限元离散方程，并结合衬砌与围岩接触面的初始条件，可以推导出两介质的时域有限元逐步积分格式。

经过有限元离散后，地下厂房结构模型可以看作是多质点组成的多自由度体系，地震作用下围岩的动力平衡方程可以表示为

根据时域加权残数的显式逐步积分格式求解岩体运动方程，可以得到岩体介质运动方程的时域显式积分表达式为

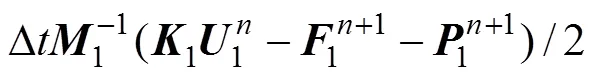
依此类推，衬砌混凝土介质动力平衡方程为

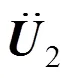
同样，衬砌混凝土介质运动方程的时域显式积分表达式为

假设围岩介质和衬砌混凝土介质静力开挖后的状态为初始条件，则有

2.2 围岩与衬砌动力相互作用分析

围岩与衬砌间相互作用关系可以看作是两介质在接触面处变形不连续，而应力连续。两介质在接触面对应节点处的相对位移可以表示为

由接触面对应节点处的相对位移引起的节点力增量可以表示为

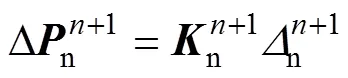
由+1时刻接触面节点力增量可以得到此时的节点力为

由于式(36)和式(37)中法向和切向接触力是在围岩与衬砌弹性接触状态下求得，而围岩与衬砌接触面是地下厂房结构中薄弱部位，其在地震循环荷载作用下的损伤是不可忽视的，因此需要对接触面损伤后的接触力进行修正。

接触面的破坏形式主要是沿法向的张拉开裂和沿切向的剪切滑移。本文作者从这2个方面对接触状态进行校核并修正接触力。

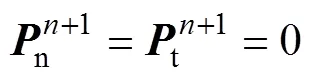
图1 围岩与衬砌非连续变形的动力分析流程图

3 工程实例

3.1 工程介绍

映秀湾水电站位于四川省汶川县映秀镇的岷江干流上，其地下厂房埋深约200 m，主厂房长×宽×高为52.8 m×17.0 m×37.2 m，主厂房边墙衬砌厚0.5 m，顶拱厚0.9 m左右，主变洞长×宽×高为59.4 m× 7.2 m×27.9 m。水电站工程场地距汶川地震震中约 8 km，地震影响烈度高达Ⅸ度。由于其距离震中较近，相当于经受了一次地震原型实验，因此其震后地下厂房衬砌震损情况具有很强的代表性。本文作者以映秀湾水电站地下厂房为工程实例，采用课题组自主研发的动力有限元程序[35]，结合本文的混凝土衬砌动力响应分析模块，研究地下厂房混凝土衬砌地震作用下的响应特征。

3.2 有限元模型与计算条件

选取映秀湾水电站主厂房和主变洞来建立数值模型。模型采用8节点6面体单元进行离散，共划分为97 652个单元，其中混凝土衬砌单元7 298个，整体三维有限元模型剖面如图2所示。取=0平面为典型断面，取该断面主厂房和主变洞衬砌上共6个监测点为研究对象。衬砌有限元模型和监测点分布如图3 所示。

在衬砌结构进行动力分析之前，需要对地下厂房进行开挖和支护模拟，将静力计算的结果作为动力响应分析计算的初始条件。计算采用的材料物理力学参数如表1所示。

图2 有限元模型剖面

(a) 主厂房衬砌；(b) 主变洞衬砌

表1 模型材料力学参数表

模型四周采用自由场人工边界，底部采用黏弹性人工边界，顶部模拟至自由面。地震波采用距汶川地震较近的卧龙台测得的加速度时程，截取其中变化剧烈、幅值较大的20~40 s时段，经过滤波、基线校正和幅值折减、坐标转换[5]后，作为地震输入波从模型底部输入。输入地震波在3个方向的加速度时程曲线如图4所示。

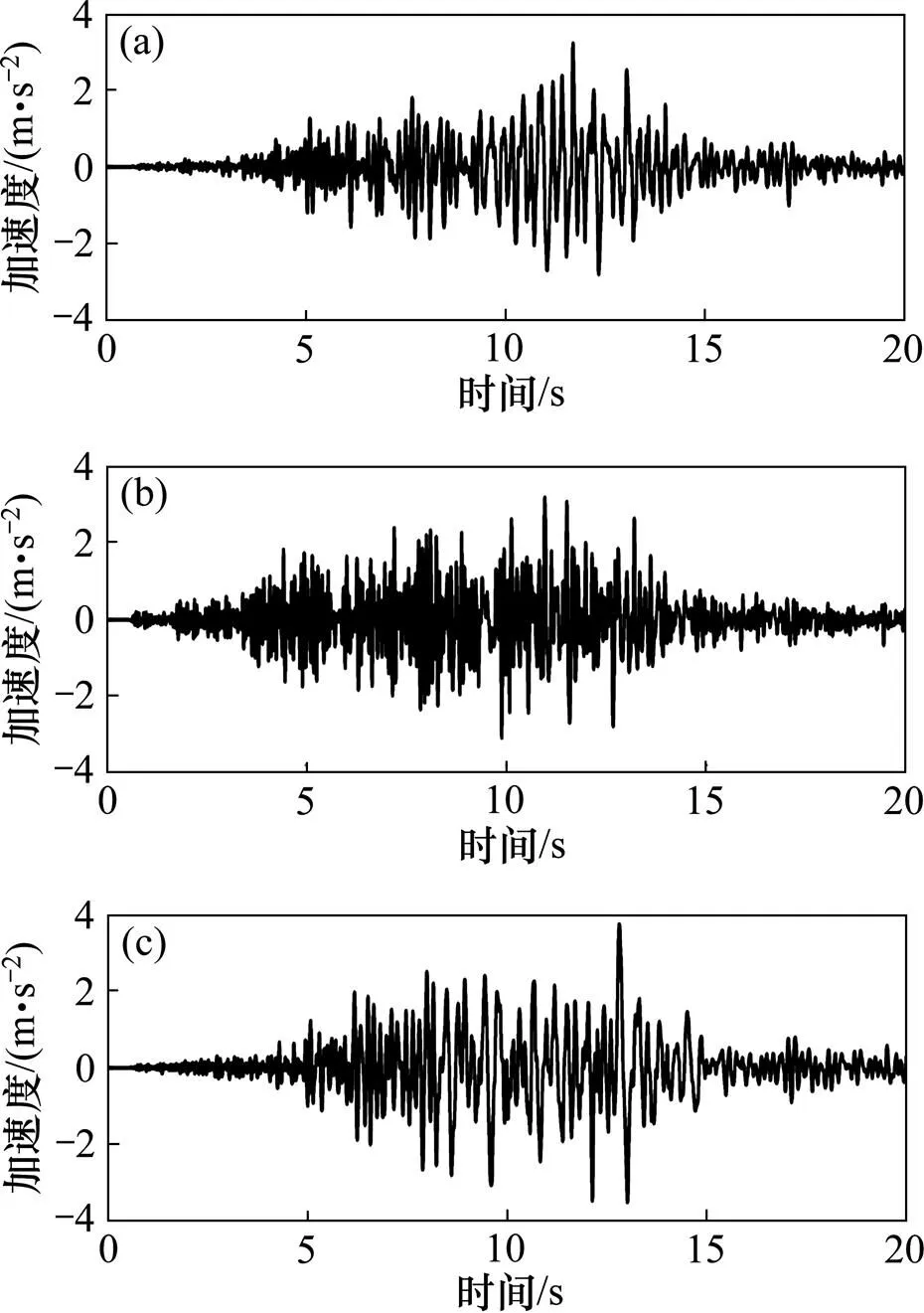
(a) X方向；(b) Y方向；(c) Z方向

3.3 地下厂房衬砌结构动力响应分析

3.3.1 衬砌监测点应力与位移时程分析

图5所示为衬砌结构6个监测点的位移时程曲线。从图5可以看出：6条时程曲线的波形和波动规律较为相似，均出现了3个明显的波峰，波峰和波谷几乎同时出现，说明衬砌结构各监测点处于同步震动状态。在0~6 s时间段内，各监测点位移变化量很小，在6 s之后，监测点位移曲线开始大幅度波动，波动范围为1.5~5.5 cm，3个波峰分别出现在10，13.2和16.5 s附近，其对应的峰值分别为4.8，5.4和5.0 cm。地震波输入完成后，监测点位移与震前相比增加了0.5~ 1.0 cm。各个监测点的位移时程曲线间的差异主要体现在波动幅值上，主厂房边墙和处位移波动幅值较小，与主厂房顶拱处的最大位移差达到1.6 cm，表明主厂房衬砌结构有较大相对变形；主变洞3个监测点位移幅值均较大，但相互之间的差值较小，说明主变洞衬砌结构主要是整体变形。

混凝土材料抗拉强度远小于抗压强度，因此拉裂破坏是混凝土材料常见的破坏形式。取，和这3个监测点的最大主应力(拉应力为正)时程进行分析，时程曲线如图6所示。开挖完成后，3个监测点的拉应力范围为0.8~0.9 MPa。随着地震荷载的施加，在0~4 s，拉应力波动幅度较小，主要在0.8~1.0 MPa范围内上下波动；在4~15 s，拉应力剧烈波动，波动范围为0.45~1.64 MPa，其中点和点的拉应力最大值分别为1.64 MPa和1.52 MPa，均超过混凝土衬砌抗拉强度；在15~20 s，拉应力波动幅度有所减小，最终拉应力为0.8~1.0 MPa，与静力开挖后的应力相比有所增加。从图6可以看出：监测点最大主应力时程曲线与输入地震波波形较为相似，拉应力的波动规律主要受到输入地震波的影响。点和点波动幅度比点的大，这表明地震波荷载对衬砌顶拱影响较大，加剧了顶拱拉应力，使得顶拱损伤破坏严重，这也与文献[32]中的调查结果相吻合。

1—A监测点；2—B监测点；3—C监测点；4—D监测点；5—E监测点；6—F监测点。

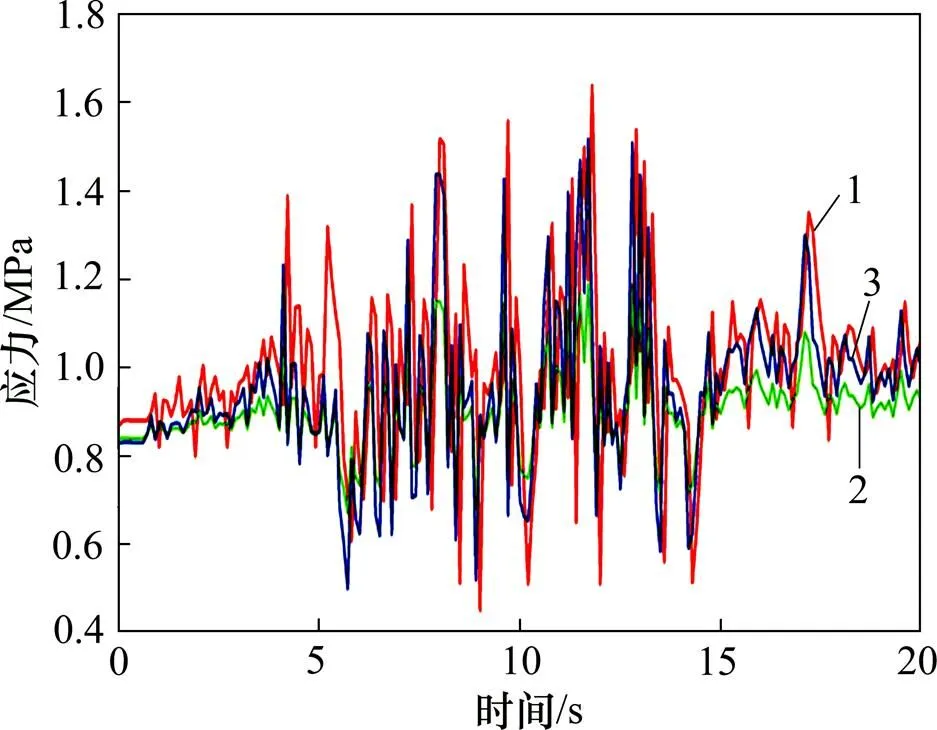
1—A监测点；2—C监测点；3—D监测点。

4.3.2 衬砌结构损伤情况分析

为了直观地显示衬砌结构损伤程度，将损伤张量d转化为标量损伤系数b，b为损伤张量主值的平均值。图7所示为衬砌结构震前和震后损伤系数分布图。由图7可知：震前(=0 s)损伤区分布在主厂房衬砌顶拱与边墙交界处、主变洞衬砌顶拱和顶拱与边墙交界处，损伤区范围较小，损伤系数主要为0.1~0.2，最大损伤系数小于0.3。在地震波输入完成后(=20 s)，衬砌结构损伤区范围和损伤系数均有较大程度增加，损伤区主要向衬砌顶拱和边墙扩展，主厂房衬砌结构顶拱大部分区域及其与边墙交界处均有不同程度损伤，主变洞衬砌结构顶拱及其与边墙交界处损伤区进一步扩大，边墙部分区域也出现了损伤情况；主厂房顶拱部分区域和顶拱与边墙交界处损伤严重，损伤系数最大值接近于1，主变洞衬砌结构损伤系数为0~ 0.8，最大损伤系数位于衬砌端部顶拱与边墙交界处。

(a) t=0 s; (b) t=20 s

震后衬砌结构拉、剪损伤分布情况如图8所示。损伤区主要分布在衬砌顶拱及其与边墙交界处，并且有向边墙扩展的趋势，其中拉裂损伤分布在主厂房顶拱顶部和顶拱与边墙交界处、主变室顶拱与边墙交界处，剪切损伤主要分布在主厂房和主变室顶拱与边墙处。结合图7~8可知：拉裂损伤区域损伤系数较大，衬砌损伤破坏严重，说明在进行衬砌结构抗震设计时，需要采取措施限制衬砌结构拉裂破坏。

图8 衬砌结构拉、剪损伤分布

4.3.3 衬砌与围岩接触面滑移开裂情况分析

衬砌结构是附着在围岩上的，如果将围岩看作是一个整体，那么衬砌与围岩的整体性明显要弱于围岩自身的整体性。因此，在地震循环荷载作用下，围岩与衬砌变形的一致性较差，围岩与衬砌接触面出现滑移、开裂情况。衬砌与围岩接触面滑移与开裂区分布如图9所示。由接触面滑移、开裂分布情况可知，滑移开裂区主要分布在衬砌顶拱、边墙、顶拱与边墙交界处。结合图8和图9可知：接触面滑移、开裂区与衬砌结构损伤区分布情况较为一致，说明接触面滑移开裂区衬砌结构更容易发生损伤情况，围岩对衬砌结构的约束作用可以有效减小地震荷载对衬砌结构的损伤破坏。

图9 衬砌与围岩接触面滑移与开裂区分布

4 结论

1) 基于混凝土拉、剪损伤各向异性动力本构模型和围岩与衬砌动力接触分析方法，建立地下厂房混凝土衬砌结构动力响应分析模型，并将该模型应用于映秀湾地下厂房衬砌结构震损演化过程分析。

2) 各监测点位移时程曲线和应力时程曲线较为相似，衬砌结构各监测点在地震荷载作用下同步震动。主厂房衬砌顶拱与边墙相比，位移和拉应力波动幅度均较大，顶拱拉应力超过了衬砌抗拉强度，其位移与边墙位移最大相差1.6 cm，表明主厂房衬砌结构有较大相对变形；主变室衬砌各点位移较为接近，说明主变洞衬砌结构主要是整体变形。

3) 衬砌结构损伤区主要分布在衬砌顶拱及其与边墙交界处，并且有向边墙扩展的趋势，这与映秀湾地下厂房震害调查结果相吻合。主厂房顶拱部分区域和顶拱与边墙交界处损伤最为严重，拉裂损伤区域损伤系数较大，衬砌损伤破坏严重，需要采取措施限制衬砌结构拉裂破坏。

4) 衬砌与围岩接触面滑移开裂区与衬砌结构损伤区分布情况较为一致，说明接触面滑移开裂区的衬砌结构更容易损伤破坏，围岩对衬砌结构的约束作用有助于衬砌结构的抗震稳定性，这也印证了地下工程与地面工程相比有较强抗震性。

[1] 李海波, 朱莅, 吕涛, 等. 考虑地震动空间非一致性的岩体地下洞室群地震反应分析[J]. 岩石力学与工程学报, 2008, 27(9): 1758−1766. LI Haibo, ZHU Li, LÜ Tao. Seismic response analysis of an underground cavern groups in rock subjected to spatially non-uniform seismic ground motion[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(9): 1758−1766.

[2] 李小军, 卢淘. 水电站地下厂房洞室群地震反应显示有限元分析[J]. 水利发电学报, 2009, 28(5): 1877−1882. LI Xiaojun,LU Tao. Explicit finite element analysis of earthquake response for underground caverns of hydropower stations[J]. Journal of Hydroelectric Engineering, 2009, 28(5): 1877−1882.

[3] 李海波, 马行东, 李俊如, 等. 地震荷载作用下地下岩体洞室位移特征的影响因素分析[J]. 岩土工程学报, 2006, 28(3): 358−362. LI Haibo, MA Xingdong, LI Junru, et al. Study on influence factors of rock cavern displacement under earthquake[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(3): 358−362.

[4] 陈健云, 胡志强, 林皋. 超大型地下洞室群的随机地震响应分析[J]. 水利学报, 2002(1): 71−75.CHEN Jianyun, HU Zhiqiang, LIN Gao. Random seismic response analysis of large-scale underground caverns[J]. Journal of Hydraulic Engineering, 2002(1): 71−75.

[5] 张雨霆, 肖明, 李玉婕. 汶川地震对映秀湾水电站地下厂房的震害影响及动力响应分析[J]. 岩石力学与工程学报, 2010, 29(增2): 3663−3671. ZHANG Yuting, XIAO Ming, LI Yujie. Effect of Wenchuan earthquake on earthquake damage and dynamic response analysis of underground powerhouse of Yingxiuwan hydropower station[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(S2): 3663−3671.

[6] 崔臻, 盛谦, 冷先伦, 等. 大型地下洞室群地震动力灾变研究综述[J]. 防灾减灾工程学报, 2013, 33(5): 606−616. CUI Zhen, SHENG Qian, LENG Xianlun, et al. A review of study on seismic catastrophe of large-scale underground cavern group[J]. Journal of Disaster Prevention & Mitigation Engineering, 2013, 33(5): 606−616.

[7] 吴建营, 李杰. 考虑应变率效应的混凝土动力弹塑性损伤本构模型[J]. 同济大学学报(自然科学版), 2006, 34(11): 1427−1430. WU Jianying, LI Jie. Elastoplastic damage constitutive model for concrete considering strain rate effect under dynamic loading[J]. Journal of Tongji University(Natural Science), 2006, 34(11): 1427−1430.

[8] 吴建营, 李杰. 反映阻尼影响的混凝土弹塑性损伤本构模型[J]. 工程力学, 2006, 23(11): 116−121. WU Jianying, LI Jie. Elastoplastic damage model for concrete considering damping effects[J]. Engineering Mechanics, 2006, 23(11): 116−121.

[9] WINNICKI A, CICHON C. Plastic model for concrete in plane stress state[J]. Journal of Engineering Mechanics, 1998, 124(6): 591−602.

[10] TEDESCO J W, POWELL J C, ROSS C A, et al. A strain-rate-dependent concrete material model for ADINA[J]. Computers and Structures, 1997, 64(5/6): 1053−1067.

[11] SHKOLNIK I E. Influence of high strain rates on stress strain relationship, strength and elastic modulus of concrete[J]. Cement & Concrete Composites, 2008, 30(10): 1000−1012.

[12] 李杰, 任晓丹, 黄桥平. 混凝土黏塑性动力损伤本构关系[J]. 力学学报, 2011, 43(1): 193−201. LI Jie, REN Xiaodan, HUANG Qiaoping. A viscoplastic damage constitutive model for concrete[J]. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(1): 193−201.

[13] 肖诗云, 李宏男, 杜荣强, 等. 混凝土四参数动态本构模型[J]. 哈尔滨工业大学学报, 2006, 38(10): 1754−1757. XIAO Shiyun, LI Hongnan, DU Rongqiang, et al. Four-parameter dynamic constitutive model of concrete[J]. Journal of Harbin Institute of Technology,2006, 38(10): 1754−1757.

[14] 李庆斌, 张楚汉, 王光纶. 单轴状态下混凝土的动力损伤本构模型[J]. 水利学报, 1994(12): 55−60. LI Qingbin, ZHANG Chuhan, WANG Guanglun. Dynamic damage constitutive model of concrete in uniaxial tension and compression[J]. Journal of Hydraulic Engineering, 1994(12): 55−60.

[15] SHKOLNIK I E. Influence of high strain rates on stress-strain relationship, strength and elastic modulus of concrete[J]. Cement and Concrete Composites, 2008, 30(10): 1000−1012.

[16] 李庆斌, 邓宗才, 张立翔. 考虑初始弹模变化的混凝土动力损伤本构模型[J]. 清华大学学报(自然科学版), 2003, 43(8): 1088−1091. LI Qingbin, DENG Zongcai, ZHANG Lixiang. Dynamic damage constitutive model for concrete accounting for the difference of the initial elastic modulus[J]. Journal of Tsinghua University (Science and Technology), 2003, 43(8): 1088−1091.

[17] 林皋, 刘军, 胡志强. 混凝土损伤类本构关系研究现状与进展[J]. 大连理工大学学报, 2010, 50(6): 1055−1064. LIN Gao, LIU Jun, HU Zhiqiang. Current situation and progress of research on damage constitutive relation of concrete[J]. Journal of Dalian University of Technology, 2010, 50(6): 1055−1064.

[18] 杜成斌, 苏擎柱. 混凝土坝地震动力损伤分析[J]. 工程力学, 2003, 20(10): 170−175. DU Chengbin, SU Qingzhu.Dynamic damage of concrete gravity dams under earthquake excitation[J]. Engineering Mechanics,2003, 20(10): 170−175.

[19] 陈建云, 李静, 林皋. 基于率性损伤模型的混凝土重力坝地震响应分析[J]. 哈尔滨工业大学学报, 2005, 37(6): 786−789. CHEN Janyun, LI Jing, LIN Gao. Seismic response analysis of concrete gravity dam based on strain rate-dependant damage model[J]. Journal of Harbin Institute of Technology,2005, 37(6): 786−789.

[20] 朱维申. 粘弹塑性介质中围岩与衬砌的应力状态[J]. 力学学报, 1981, 17(1): 56−67. ZHU Weishen. Stress state of rock and lining in viscoelastic plastic rock media[J]. Chinese Journal of Theoretical and Applied Mechanics, 1981, 17(1): 56−67.

[21] 肖明, 杨建东, 赖旭. 大型长廊阻抗式尾水调压井结构受力分析[J]. 岩石力学与工程学报, 2000, 19(4): 476−480. XIAO Ming, YANG Jiandong, LAI Xu. Mechanics on large long corridor of surge tank[J]. Chinese Journal of Rock Mechanics and Engineering, 2000, 19(4): 476−480.

[22] CHEN Juntao, YANG Yang, YE Chao Three-dimensional numerical analysis of compound lining in complex underground surge-shaft structure[J]. Mathematical Problems in Engineering, 2015, 2015(1):1-10.

[23] RAPHAEL J M. Tensile strength of concrete[J]. ACI Journal, 1984, 81(2): 158−165.

[24] 林皋, 陈健云, 肖诗云. 混凝土的动力特性与拱坝的非线性地震响应[J]. 水利学报, 2003, 6: 30−36. LIN Gao, CHEN Janyun, XIAO Shiyun. Dynamic behavior of concrete and nonlinear seismic response of arch dam[J]. Shui Li Xue Bao, 2003, 6: 30−36.

[25] 肖诗云, 林皋. Drucker-Prager材料一致率型本构模型[J]. 工程力学, 2003, 20(4): 147−151. XIAO Shiyun, LIN Gao. A Drucker-Prager consistent rate-dependent model[J]. Engineering Mechanics, 2003, 20(4): 147−151.

[26] 葛修润, 蒋宇, 卢允德, 等. 周期荷载作用下岩石疲劳变形特性试验研究[J]. 岩石力学与工程学报, 2003, 22(10): 1581−1585. GE Xiurun, JIANG Yu, LU Yunde, et al. Testing study on fatigue deformation law of rock under cyclic loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(10): 1581−1585.

[27] 李杰, 任晓丹. 混凝土静力与动力损伤本构模型研究进展述评[J]. 力学进展, 2010, 40(3): 284−297. LI Jie, REN Xiaodan. A review on the constitutive model for static and dynamic damage of concrete[J]. Advances Mechanics, 2010, 40(3): 284−297.

[28] WANG S Y, SUN L, YANG C, et al. Numerical study on static and dynamic fracture evolution around rock cavities[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2013, 5(4): 262−276.

[29] ZHOU X Q, HAO H. Modelling of compressive behaviour of concrete-like materials at high strain rate[J]. International Journal of Solids and Structures, 2008, 45(17): 4648−4661.

[30] 张志国, 肖明, 陈俊涛. 大型地下洞室地震灾变过程三维动力有限元模拟[J]. 岩石力学与工程学报, 2011, 30(3): 509−523. ZHANG Zhiguo, XIAO Ming,CHEN Juntao. Simulation of earthquake disaster process of large-scale underground caverns using three-dimensional dynamic finite element method[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(3): 510−523.

[31] 杨阳. 水电站地下厂房围岩与结构地震响应分析[D]. 武汉: 武汉大学水利水电学院, 2015: 18. YANG Yang. Seismic response analysis of surrounding rock and structure for underground powerhouse of hydropower station[D]. Wuhan:Wuhan University. School of Water Resources and Hydropower Engineering, 2015: 18.

[32] 尹显俊, 王光纶. 岩体结构面切向循环加载本构关系研究[J]. 岩石力学与工程学报, 2005, 24(7): 1158−1163. YIN Xianjun, Wang Guanglun. Study of consititutive model for rock interfaces and joins under normal cyclic loading. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(7): 1158−1163.

[33] GRASSELLI G, EGGER P. Constitutive law for the shear strength of rock joints based on three-dimensional surface parameters[J]. International Journal of Rock Mechanics and Mining Sciences, 2003, 40: 25−40.

[34] BANDIS S C, LUMSDEN A C, BARTON N R. Fundamentals of rock joint deformation[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1983, 20(6): 249−268.

[35] 张志国, 肖明, 张雨霆, 等. 大型地下洞室三维弹塑性损伤动力有限元分析[J]. 岩石力学与工程学报, 2010, 29(5): 982−989. ZHANG Zhiguo, XIAO Ming,ZHANG Yuting, et al. Dynamic finite element analysis of large-scale complex underground caverns with three-dimensional elastoplastic damage model[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(5): 982−989.

(编辑 伍锦花)

Stability analysis of concrete lining structure in underground powerhouse with seismic action

WANG Xiaowei1, 2, CHEN Juntao1, 2, XIAO Ming1, 2, DENG Jian1, 2

(1. State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China;2. Key Laboratory of Rock Mechanics in Hydraulic Structural Engineering, Ministry of Education, Wuhan University, Wuhan430072, China)

Based on rate-dependant and fatigue damage characteristics of concrete under cyclic loading, a dynamic constitutive model that considers tension and shear damage anisotropic was proposed, and the evolution equations of damage variables were derived. According to dynamic interaction characteristics of surrounding rock and lining, a explicit dynamic finite element analysis method that considers the discontinuous deformation between surrounding rock and lining was presented. Thus, a dynamic response analysis method of concrete lining structure in underground powerhouse was constructed and then applied to calculate seismic stability of Yingxiuwan Hydropower Station. The results show that various positions of lining structure are in a synchronous vibration state, but the stress and displacement response of the top arch are larger than that ofother positions. The maximum relative displacement of the top arch and side wall of the main powerhouse reaches 1.6 cm, indicating that the main building has a obvious structural deformation. Damage zone of lining structure is mainly distributed in its top arch, and the damage caused bytension is more serious. The confinement effects of the surrounding rock to the lining structure is helpful for seismic stability of the lining structure. Calculation results from the proposed method reflect seismic response characteristics of concrete lining reasonably, and thus provide references for seismic design of concrete lining in underground powerhouse.

underground powerhouse; concrete lining; dynamic response; tension and shear damage anisotropic; dynamic constitutive; discontinuous deformation; explicit dynamic finite element

10.11817/j.issn.1672-7207.2018.05.023

TV45

A

1672−7207(2018)05−1203−10

2017−05−08；

2017−06−28

国家重点基础研究发展计划(973计划)项目(2015CB057904)；国家自然科学基金资助项目(51579191) (Project(2015CB057904) supported by the National Program on Key Basic Research Project (973 Program); Project(51579191) supported by the National Natural Science Foundation of China)

陈俊涛，博士，副教授，从事地下工程和工程软件开发等方面的研究；E-mail: chenjt000@163.com