基于伯克霍夫插值多项式的秘密共享方案
2018-05-29葛文庚
葛文庚
(黄淮学院 信息工程学院,河南驻马店 463000)
0 引 言
传统的加密算法以及签名和认证机制能够维护数据的安全性与完整性,然而如果只采用加密技术是无法确保数据安全的,这是由于加密技术的安全强度依赖于信息系统数据安全的强度,但是大部分加密技术的安全性是对于其密钥的保密,并且一般加密算法也是公开的,这就使得如果出现密钥丢失的情况将会导致整个信息系统失去安全性[1]。因此,如何保护密钥安全成为维护整个信息系统数据安全的关键问题。国内外学者对于密钥的管理(例如,密钥产生、存储、传输等)问题进行了较为丰富的研究,但是传统的加密技术不能完全确保数据的保密性与完整性。秘密共享策略为密钥管理提供了有效的安全平台[2-3],它包括分发者与参与者,分为秘密分发、验证和恢复三个阶段。秘密共享策略的主要方法是:首先,分发者采用秘密分发算法给每个参与者产生一个份共享;然后,通过安全信道将份共享传输给每一个参与者,并且确定恢复秘密的授权参与者集合的访问结构;最后,参与者提交自己的共享,如果能够满足访问结构的要求,即可进行秘密恢复[4]。随着秘密共享策略的研究不断深入,国内外研究人员相继提出了各类不同的秘密共享方案[5-7]。1979年,Shamir[8]和Blakley[9]分别独立地提出了秘密共享方案,前者是基于拉格朗日插值公式,后者则是基于射影几何学。Harn[10]给出了一种基于(t,n)门限的可验证多秘密共享方案,改方案可以通过验证识别分发者和参与者的欺骗问题。Heidarvand等人[11]通过采用双线性映射计算方程,给出了一种公开的可验证多门限秘密共享方案,其可以更易识别分发者和参与者的不诚实行为。Bu等人[12]给出了一种基于NTBU算法的秘密共享方案,然而其只能恢复单个秘密且存储量也较大。Li[13]通过利用多维空间参数和超法面交点构建参与者共享主密钥,给出了一种安全完备、直观实用的(s,n)门限秘密共享方案。Fan等人[14]给出了一种无可信方的非线性门限秘密共享方案,主要是利用混沌算法与有限状态自动机两种非线性结构,产生具有随机性和动态性的子密钥,参与者通过控制实现可一次一密的安全级别,可防止欺骗和合谋攻击。而文中通过利用伯克霍夫插值多项式和离散对数安全性,给出了一种基于伯克霍夫插值多项式的秘密共享方案(a Secret Sharing scheme based on Birkhoff Interpolation Polynomial, SSBIP),该方案能够有效识别并防止参与者和分发者的欺诈行为,具有非常良好的适应性。
1 背景知识介绍
下面给出伯克霍夫插值的简要描述[15]:定义一个三元组〈X,E,C〉。其中,X={x1,…,xk}是实数域中一组给定的数,且x1 P(j)(xi)=ci,j(i,j)∈I(E) (1) 式中,P(j)(·)表示为P(x)的第j次导数。RN-1[x]表示为小于N-1阶的全部可能的多项式集合。 (2) 其中,|·|表示行列式运算。 采用矢量C′对式(2)进行变换可得: (3) 式中,Ai(E,X,φj)是由A(E,X,φ)去除第(i+1)行与第(j+1)列得到的。根据式(3)可得: (4) 令φ={g0(x)=1,g1(x)=x,…,gN-1(x)=xN-1},则有g0(0)=1,gj(0)=0,其中1≤j≤N-1。由此可以计算出P(0)如下式所示: (5) 秘密共享是指秘密分发者将秘密s分割成n份共享s1,s2,…,sn,并把这些共享秘密地分发给所有参与者,获得授权的子集中的所有参与者可以通过分享自己所拥有的共享,最后共同合作恢复出初始秘密s。如果少数参与者想要实施欺诈,故意分享错误的共享或是由于网络传输错误等原因导致共享错误,这种情况下即使是获得授权的子集也无法恢复出秘密。所给SSBIP算法是一种可验证的秘密共享方案,主要包括系统初始化、秘密分发、秘密验证和秘密恢复四个阶段。 阶段一:系统初始化 假设U={P1,P2,…,Pn}为n个参与者的子集,它们被分成m+1个等级U0,U1,…Um。如果将U0级中的参与者是P1,P2,…P|U0|,则U1级中的参与者则是P|U0|+1,P|U0|+2,…,P|U0+U1|。且有|Ui|是Ui中参与者的个数。 阶段二:秘密分发 秘密分发者生成多项式f1(·)与f2(·),如式(6)所示: (6) 式中,a0=s表示是所需分享的秘密,a1,…,at-1和b0,…,bt-1是Zq域中的随机数。 阶段三:秘密验证 为了能确保可以恢复出真实的秘密,则需要验证所接收的共享是否存在欺诈行为。所有参与者收到共享之后,则需验证该共享是否满足下式: (7) 阶段四:秘密恢复 所给SSBIP算法的可验证性主要是证明在秘密恢复阶段,参与者不能够提供错误的共享以及证明分发者不能分发不正确的共享。 (8) 证明 伯克霍夫插值问题良好的适应性表明在授权子集AS中的参与者的共享可以定义两个独立的t-1次多项式F1(x)与F2(x)满足: (9) (10) 令Cj=gcj,且有j=0,1,…,t-1,则可得: (11) 假如所给SSBIP算法受到攻击。令B={Pβ1,…,Pβl}表示被攻击的未授权的参与者子集,此时秘密s可以是Zq域内的任意值。令B′=B∪{0},其中0∈U0为一个虚假的参与者。则在B′集内被授权的子集可以定义两个多项式F1(·)与F2(·)。令B″为B′集中任意的已授权子集。此时,{0}也肯定为B″集中的一个成员,因此不失一般性。令B″={0,Pβ1,…,Pβt-1},则对于任意s∈Zq,一定存在s′∈Zq,满足下式: gshs′=C0 (13) 同时,也存在使得F1(0)=s与F2(0)=s′的两个唯一的多项式F1(·)与F2(·),满足下式: (14) 其中,Pβi∈Uki,Uk是第k个等级,t=1,…,t-1。 假定存在两个多项式F1(·)与F2(·),即有: (15) 则根据定理1可知,多项式F1+dF2(x)是唯一的t-1次多项式可以满足下式: (16) 所给SSBIP方案在Shamir门限秘密共享方案的基础上,通过利用伯克霍夫插值多项式和离散对数困难性,给出了一种有效的秘密共享方案。性能分析表明,该方案中参与者不能故意或是因网络传输错误等原因提供错误的共享,同时分发者也不能提供不正确的共享,并且所给方案广播的参数也不会泄露有关秘密的任何信息,可以有效确保所给方案的安全性。因此,所给SSBIP方案具有非常优良的适应性,能应用于各类不同的应用系统中。 : [1] 韩益亮, 岳泽轮, 杨晓元, 等. 标准模型下可证明安全的多变量加密方案[J]. 华中科技大学学报(自然科学版),2014,42(11): 47-51. [2] 宋云, 李志慧, 李永明. 含至多四个参与者的量子密码共享方案的最优信息率[J]. 电子学报,2014,42(10): 1951-1956. [3] Chae C J, Choi K N, Choi K, et al. Enhanced Biometric Encryption Algorithm for Private Key Protection in BioPKI System[J]. Journal of Central South University, 2011, 21: 4286-4290. [4] 焦栋. 门限秘密共享策略及其应用研究[D]. 大连:大连理工大学, 2014. [5] Massoud H D, Elham F. A Novel and Efficient Multiparty Quantum Secret Sharing Scheme Using Entangled States[J]. Sci China-Phys, Mech Astron, 2012, 55: 1828-1831. [6] Lee Y S, Wang B J, Chent H. Quality-improved Threshold Visual Secret Sharing Scheme by Random Grids[J]. IET Image Processing, 2013, 7(2): 137-143. [7] 蓝才会, 王彩芬. 一个新的基于秘密共享的条件代理重加密方案[J]. 计算机学报,2013,36(4): 895-902. [8] Shamir A. How to Share a Secret[J]. Communication of ACM, 1979, 22(11): 612-613. [9] Blakley G R. Safeguarding Cryptographic Keys [C]//Proc of AFIPS 1979, National Computer Conference. New York, USA: AFIPS Press, 1979, 48: 313-317. [10] Harn L. Efficient Sharing (Broadcasting) of Multiple Secrets[J]. IEE Computers and Digital Techniques, 1995, 142(3): 237-240. [11] Heidarvand S, Villar J L. Public Verifiability from Pairings in Secret Sharing Schemes[C]// SAC 2008 LNCS, 2008: 294-308. [12] 步山岳, 于坤, 王汝传. 一种基于NTRU算法的秘密共享方案[J]. 小型微型计算机系统, 2009,30(10): 1986-1987. [13] 李滨. 基于多维空间参数曲线的门限秘密共享方案[J]. 浙江大学学报(理学版),2014,41(5): 518-521. [14] 范畅, 茹鹏. 非线性一次一密(t,n)门限秘密共享方案[J]. 计算机应用,2013,33(9): 2536-2539. [15] 刘莉莉, 陈少田, 夏朋, 等. 一元Birkhoff型有理插值问题[J]. 吉林大学学报(理学版),2011,49(3): 369-372. [16] Nasrollah P, Mahnaz N, Ziba E. Distributed Key Generation Protocol with Hierarchical Threshold Access Structure[J]. The Institution of Engineering and Technology, 2015, 9(4): 248-255.
2 SSBIP算法
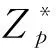
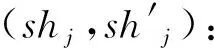
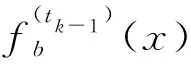
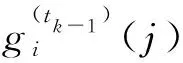
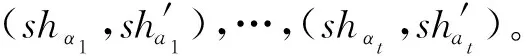
3 性能分析
3.1 可验证性
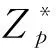
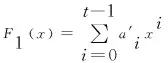
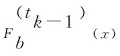
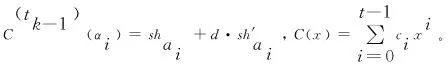
3.2 安全性
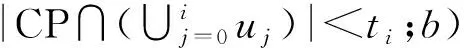
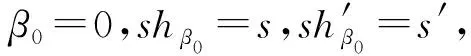
4 结 语
