基于ELM-AE的迁移学习算法∗

邓万宇 屈玉涛 张 倩

（西安邮电大学计算机学院 西安 710061）

1 引言

互联网和社交网络的快速发展，带来了数据（例如，Web数据）的爆发式增长［11］。数据种类的增多导致实际应用中经常需要处理来自于不同领域的数据。由于数据特征之间的差异较大，导致很难训练出一种公共分类器去分类不同类别的数据，在这种情况下就需要使用迁移学习。迁移学习［15］的主要目的是训练一种健壮的公共分类器，可以很好地对来自于不同领域的数据进行分类。迁移学习广泛应用在自然语言处理［16～18］，计算机视觉［18～20］，统计和机器学习［18～20］中。传统的迁移学习有很多都是基于主成分分析法（PCA）［6，9～10］来实现的。PCA［5，12］是在尽量不改变数据特征的情况下来降低数据的维度，它是考察多个变量间相关性的一种多元统计方法，研究如何通过少数几个主成分来揭示多个变量间的内部结构，即从原始变量中导出少数几个主成分，使它们尽可能多地保留原始变量的信息，且彼此间互不相关。PCA所要做的就是设法将原来众多具有一定相关性的变量，重新组合为一组新的相互无关的综合变量来代替原变量。然而PCA具有它的局限性：1）它要求数据必须是线性的。2）它分解出的特征必须是正交的。这导致在实际应用中很多数据都无法应用PCA来进行处理。

本文使用一种新的特征提取方法，即极限学习机自编码（ELM-AE）。基于ELM-AE来完成迁移学习，它可以解决PCA应用中的局限性，并在迁移学习上获得更高的分类准确率。

迁移学习的最基本的实现方法是将原始数据映射到一个新的空间中，在这个空间中，源域和目标域的特征之间的差异被最小化。基于PCA的迁移学习算法已经被广泛的研究［6，9～10］，通过 PCA 可以找到一个公共的特征子空间。在文献［8］中Blitzer等提出了一种方法，通过不同领域之间的特征关系去学习一个新的特征空间。在Chang［15］表示源域数据可以通过目标域数据线性变换而得到。在 Gong等［7］提出了一个 geodesic flow kernel（GFK），它主要统计源数据和目标数据在几何和统计上特征的改变。Fernando等［3］提出了一种基于PCA的迁移学习算法，他们应用PCA分别得到源域数据和目标域数据的特征空间，然后将源域数据特征映射到目标域数据的特征空间中或者将目标域数据的特征映射到源域数据的特征空间中。

2 ELM-AE

极速学习机自编码器（ELM-AE）是一种基于极速神经网络（ELM）的自编码器，具有ELM的计算速度快，效率高等优点。和传统的ELM［14］神经网络类似，ELM-AE的网络结构包含三层：输入层，隐含层和输出层。唯一不同之处在于ELM-AE的目标输出和它的输入是相等的，其网络结构如图1所示。

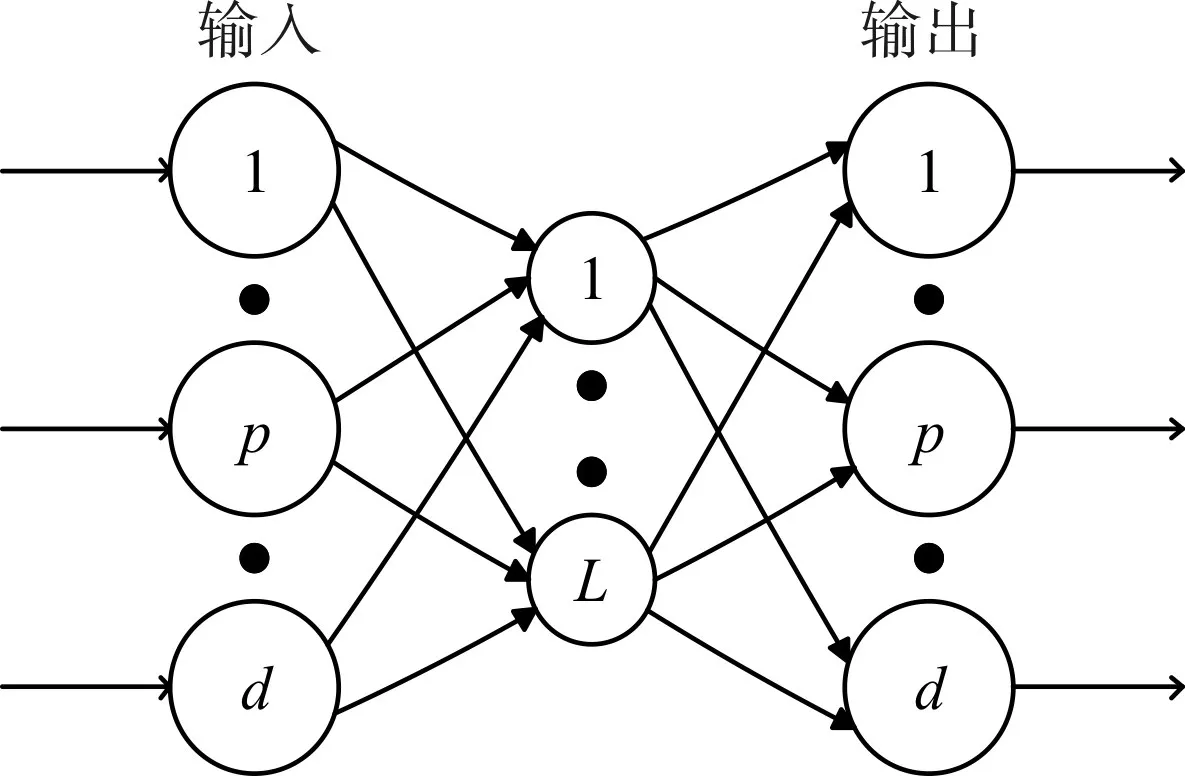
图1 ELM-AE网络结构

在图1中，L代表的是隐含节点数，d代表的是输入层和输出层的节点数，也就是数据的维度，x代表的是ELM-AE的输入和输出。根据d和L之间的关系，ELM-AE可以被分为三种不同的类型。

压缩型：代表数据从高维空间映射到低维空间中。

稀疏型：代表数据从低维空间映射到高维空间中。

等维型：代表数据映射前后的维度是相等的。

根据ELM的理论［4，14］，隐含层的参数可以随机地生成。通常可以选择正交的隐含层参数来提高ELM-AE的泛化性能。隐含层的参数可以通过Johnson-Lindenstrauss lemma［13］来计算得到：

在式（1）中 a=是随机正交的权重，b=[b1，…，bL]是随机正交的偏差。对于压缩型和稀疏型的ELM-AE，计算ELM-AE的输出权值β可以通过式（2）：

-1

其中，H=[h1，…，hN]是ELM-AE的隐含层输出，C是ELM的输入参数，I是标准单位矩阵，X=[x1，…，xN]是ELM-AE的输入和输出。对于等维型ELM-AE，计算它的输出权值 β可以通过式（3）：

式（2）的奇异值分解（SVD）可以表示为

其中u是HHT的特征向量，d是H的奇异值，H是输入X在隐含层空间上的映射，所以ELM-AE的输出权值β通过奇异值可以对输入数据进行特征表达，通过β可以将输入数据映射到对应的特征子空间中。

3 基于ELM-AE的子空间对齐

在实际应用中，数据通常来源于不同领域，例如图片和文本混合的数据，如果使用图片的数据来训练一个分类器，并用它来分类文本的数据，通常不会获得好的分类效果。迁移学习可以很好地解决此类问题。

ELM-AE的输出权β可以通过奇异值来对输入数据进行特征表达，因此通过ELM-AE可以得到源域数据和目标域数据各自的特征子空间，分别记为WS和WT（WS，WT∈RD×L）。D表示的是数据的维度，L表示的是ELM-AE的隐含层节点数。由于源域数据和目标域数据分布不同，映射出的特征子空间也各不相同。通过子空间对齐将源域和目标域的特征子空间映射到一个公共的特征空间中，在该公共特征空间中，源域数据和目标域数据之间的特征差异被最小化。这样通过公共特征子空间上的数据来训练的分类器可以很好地分类来自不同域的数据。

假设源域数据为 xS，目标域数据为 xT，xS，xT∈R1×D，则源域和目标域的特征子空间 X͂S和X͂T可以被分别表示为 ySWS和 yTWT。为了将源域特征子空间 X͂S和目标域特征子空间 X͂T映射到一个公共特征子空间中，在此需要学习一个转换矩阵M ，通过M 使WS和WT对齐。根据文献［3］，M可以通过最小化Bregman矩阵求解：

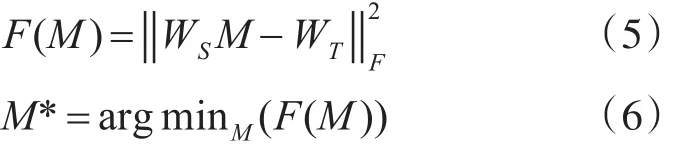
其中是Frobenius范数。由于Frobenius范数的正交不变性，式（5）可以写成

由式（7）可以求得最优的转化矩阵M ：

通过转化矩阵M，可以得到子空间对齐后的新的映射空间：

W͂a就是目标域特征子空间对齐源域特征子空间后的公共特征空间。

4 算法实现

基于ELM-AE的子空间对齐算法的实现主要分两个环节：子空间生成；子空间对齐。其主现现步骤为：首先初始化ELM-AE，计算输入数据的输出权值，生成对应的特征子空间。其次，利用生成的特征子空间求解出转化矩阵M。最后利用转化矩阵将各自的特征空间进行对齐。基于ELM-AE的子空间对齐算法流程见算法1。

算法1：基于ELM-AE的子空间对齐算法

输入：源域数据XS，目标域数据XT，源域数据标签TS，目标域数据标签TT，隐含层节点数 L，激活函数 h(x)。

输出：预测的目标域标签 TT

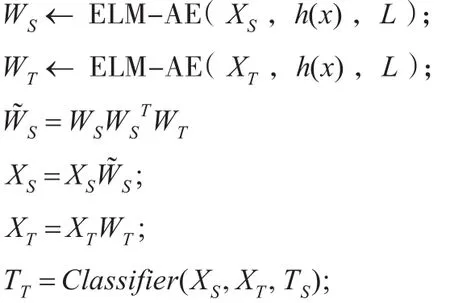
5 实验验证

本次实验选取 Office［1］和 Caltech256［2］数据集来进行算法的验证。Office数据集上包含webcam图片（W），DSLR图片（D）和 Amazon图片（A）。Caltech256中的图片被标记为C。数据集共包含4个不同领域的数据。A，W，D和C可以组成12组迁移学习问题。迁移学习可以被标记为S→T，S代表源数据域，T代表目标数据域。

本实验将基于ELM-AE的迁移学习算法与其他几种常见的迁移学习算法进行了比较，每组迁移学习分别使用KNN和SVM作为最终分类器，实验结果如表1所示。

表1 （Part I）.KNN分类器的分类准确率（Office dataset+Caltech256）

表2 （Part I）.SVM分类器的分类准确率（Office dataset+Caltech256）

6 实验结果分析

在上述实验结果中，表1和表2均被分为两个部分。NA表示的是在该组迁移学习中不涉及特征映射。GFK［7］主要统计源数据和目标数据在几何和统计上特征的改变。PCA［3］表示应用PCA分别得到源域数据和目标域数据的特征空间，然后将源域数据特征映射到目标域数据的特征空间中或者将目标域数据的特征映射到源域数据的特征空间中。DA-SA1［3］表示源数据通过PCA来求得源数据的目标子空间WS。DA-SA2［3］表示目标域数据利用PCA得到目标域子空间WT。表1使用KNN作为最终分类器，在表1的12组迁移学习中，有8组在准确率方面提升明显。表2使用了SVM作为最终分类器，表2中的迁移学习中有11组迁移学习获得了更高的分类准确率。实验结果表明不论最终分类器是选择KNN还是SVM，基于ELM-AE的迁移学习算法都可以获得更高的分类准确率，这证明了基于ELM-AE的迁移学习算法拥有更好的应用性。

7 结语

基于ELM-AE的迁移学习算法相比传统的迁移学习算法拥有着更好的效率。由于ELM-AE和ELM一样在计算过程中不需要迭代，因此计算速度快。相比于PCA，ELM-AE可以很好地处理那些非线性的数据问题。随着数据种类的增多，基于ELM-AE的迁移学习算法在未来会获得更加广泛的应用。

［1］Saenko K，Kulis B，Fritz M，et al.Adapting Visual Category Models to New Domains［J］.ECCV，Heraklion，Greece，September 2010：213-226.

［2］Gopalan R，Ruonan L，Chellappa R.Domain adaptation for object recognition：An unsupervised approach［J］.2011，24（4）：999-1006.

［3］Fernando B，Habrard A，Sebban M，et al.Unsupervised Visual Domain Adaptation Using Subspace Alignment［C］//IEEE International Conference on Computer Vision.IEEE，2014：2960-2967.

［4］Kasun L L C，Zhou H，Huang G B，et al.Representational Learning with ELMs for Big Data［J］.Intelligent Systems IEEE，2013，28（6）：31-34.

［5］Jolliffe I T.Principal Component Analysis［J］.Journal of Marketing Research，2002.

［6］Chen B，Lam W，Tsang I，et al.Extracting discriminative concepts for domain adaptation in text mining［C］//ACM SIGKDD International Conference on Knowledge Discovery and Data Mining，Paris，France，June 28-July.DBLP，2009：179-188.

［7］Gong B，Shi Y，Sha F，et al.Geodesic flow kernel for unsupervised domain adaptation［C］//IEEE Conference on Computer Vision and Pattern Recognition.IEEE Computer Society，2012：2066-2073.

［8］Blitzer J，Mcdonald R，Pereira F.Domain adaptation with structural correspondence learning［J］.Emnlp，2006：120-128.

［9］Pan S J，Kwok J T，Yang Q.Transfer learning via dimensionality reduction［C］//AAAI Conference on Artificial Intelligence，AAAI 2008，Chicago，Illinois，Usa，July.DBLP，2008：677-682.

［10］Pan S J，Tsang I W，Kwok J T，et al.Domain adaptation via transfer component analysis［J］.IEEE Transactions on Neural Networks，2011，22（2）：199.

［11］Torralba A，Efros A A.Unbiased look at dataset bias［C］//Computer Vision and Pattern Recognition.IEEE，2011：1521-1528.

［12］Zwald L，Blanchard G.On the Convergence of Eigenspaces in Kernel Principal Component Analysis［C］//2005：1649-1656.

［13］Johnson W B，Lindenstrauss J.Extensions of Lipschitz maps into a Hilbert space［J］.1984，26（189）：189-206.

［14］Huang G B，Chen L，Siew C K.Universal approximation using incremental constructive feedforward networks with random hidden nodes［J］.IEEE Trans Neural Netw，2006，17（4）：879-892.

［15］Jhuo I H，Liu D，Lee D T，et al.Robust visual domain adaptation with low-rank reconstruction［C］//Computer Vision and Pattern Recognition.IEEE，2012：2168-2175.

［16］Iii H D.Frustratingly Easy Domain Adaptation［J］.ACL，2009.

［17］Leggetter C J，Woodland P C.Maximum likelihood linear regression for speaker adaptation of continuous density hidden Markov models［J］.Computer Speech&Language，1995，9（2）：171-185.

［18］Huang J，Smola A J，Gretton A，et al.Correcting sample selection bias by unlabeled data［C］//International Conference on Neural Information Processing Systems.MIT Press，2006：601-608..

［19］Ben-David S，Blitzer J，Crammer K，et al.Analysis of representations for domain adaptation［C］//International Conference on Neural Information Processing Systems.MIT Press，2006：137-144.

［20］Pan S J，Yang Q.A Survey on Transfer Learning［J］.IEEE Transactions on Knowledge&Data Engineering，2010，22（10）：1345-1359.