预测Motifs算法的改进评价策略∗
2018-05-29张斐
张 斐
(陕西警官职业学院警察技术系 西安 710021)
1 引言
所谓Motifs(模体)指的是在一组相关的蛋白质或者DNA序列中重复出现的具有生物意义的序列模式,它能够代表一个蛋白质家族,随着计算机技术在生物领域的不断成熟和推广,关于生物序列中Motifs的自动预测技术已经成为一门新兴技术,如何设计出预测算法以更好地对生物信息进行研究就成为了生物信息领域一个重要的研究课题。
一个蛋白质家族所有的或大多数的成员共同拥有的Motifs极可能是该家族执行某些重要功能或组成结构不可或缺的部分。预测出一个蛋白质家族共同的Motifs就能刻画该家族特征,从而可以利用这些特征来进行发掘蛋白家族新成员等有意义的新发现。但是对于通过各种生物信息学方法识别的Motifs,目前没有很好的办法辨别真假和优劣[1]。
本文通过研究对不同Motifs预测算法在同一数据集上测试后的评价策略,针对传统的算法预测问题,采用新的评价方案和评价标准对算法预测的结果进行分析。
2 算法的种类
Motifs预测是将生物序列中的氨基酸或碱基转化成为相应的字符串,在不同字符串序列中寻找最大公共子串,再通过生物学特征将这些字符串提取,与通过实验方法获得的生物信息数据库进行匹配。寻找最大公共子串的算法设计思想和数学模型是Motifs预测的关键。Motifs预测方法分为两类:统计学方法,如Gibbs采样算法、MEME和HMMER 等 ;确 定 性 方 法 ,如 Pratt、TEIRESIAS、SPLASH以及SPAT等,这些算法均能发现隐藏在序列中的弱模体(weak Motifs),但统计学Motifs预测方法在实际应用更为广泛。
统计学Motifs预测算法遵循了不同的数学方法和原理,但都避免不了自身的不足,例如Gibbs采样算法虽具有简单、计算速度快的优点,但却是局部优化算法,不能保证结果的全局最优性。而EM算法较好解决了具有隐变量模型的估计,但对于较短模体,EM算法极易陷入局部极值,从而得不到最优解[2]。
3 主要算法描述
3.1MEME算法
MEME算法是基于最大期望值(EM)算法来识别Motifs的一种迭代算法,它交替执行两个步骤:期望值步骤E和最大值步骤M[3]。在步骤E中,通过给出的观察数据和W的现有估计值,计算出隐变量的分布。在步骤M中,通过步骤E给出的隐变量的假定分布,计算出参数的最优值。
算法1
Begin:
Input(输入序列 s={s1,…,sN}):
初始化变量:
LengthM(待处理的Motifs的长度)
NumberM(识别不同的Motifs的数目)
Iterative(设定的迭代次数)
EM(I)(在数据集中所期望每个Motifs出现的算法Algo
rithm()):
{
For Motifs=1 to NumberM
{
For(数据集中的每个子序列根据从子序列得到的起
始位置);
运行修改后的EM;
共迭代Iterative次;
EndFor
}
EndFor
给定W和λ(0)选择初始参数值θ(0);执行EM算法后建立新模型;释放数据;
集中处理得到的Motifs
}
在循环中,EM算法[4]选择随机的起始位点来迭代运行。其中,起始位点所输入的数据集中的子序列得到的,而只有那些能使模型取得最大可能性值的起始位点被选中,EM算法从这个起始位点开始运行并最终迭代若干次后,得到一个相对稳定值后结束。
3.2 基于贪心EM算法的改进预测算法(PKGE算法)
PKGE是基于Kd-树的贪心EM预测算法,Kd-树是通过定义一个递归的二进制的K维数据集,它的根节点包括全部数据,每一层通过检测不同属性(关键字)值以决定选择分支的方向,从而加快查询速度。所以算法的时间复杂度比较高,只适用于寻找短序列的 Motifs[5]。
算法执行的步骤如下。
算法2
Begin:
设N条序列,长度从数据集中取值。
初始化字符串X={xi}(i=1,…,n),满足n
While(Kd-树结构→保守序列→K值最优)
{
For(依次扫描所有序列)
Kd-树来处理数据集X,通过质心C找到一致性序列
EndFor
}
参数迭代:
设置模型划分度
While(局部EM优化→g划分→似然度最优)
{
For(参数迭代扫描)
初始值执行EM
g+1划分的混合模型
EndFor
}
求出Motifs的最大数量
算法描述了在Motifs预测中的一个混合Motifs模型。通过引入Kd-树结构,使数据集中,似然函数单调增加,彻底搜索候选序列部分的参数,从而使得其它Motifs大量存在的可能性大大降低。
4 评价策略
算法测试的硬件系统环境为IBMX365服务器、联想PC。软件系统环境为Win7(Matlab 7.1)、Linux red hat 9.0(MEME 3.4.5)。评价中采用的统计软件有SigmaPlot9.0、SPSS22.0。
利用训练数据集和测试数据集验证。在实验中依据经验值将参数λ设置成0.8,并设置K=1来指定一个Motifs的相邻矩阵,参数T的值为T=N/2(序列长度的一半)[5]。
对比使用MEME算法来进行验证。其中在MEME中选择的是anr模式即任意重复数量模式,评价策略见图1。

图1 评价策略图
4.1 采用训练数据集的实验
从PRINTS数据库下载部分蛋白质家族序列,随机产生10条长度在200bp~250bp之间的蛋白质序列,通过多次比对设定Kd-树划分值为6,叶子节点字符串的长度设定为 5,Motifs长度为 10[5],由于选定序列源于生物数据库,虽经过人工拼接,但仍有部分片段保留,因而程序执行后仍能找到8个Motifs。
4.2 采用测试数据集的实验
4.2.1 Fingerprints法测试
我们选择的PRINTS数据库[6]包含了大量蛋白质家族,每个家族成员中都有Motifs出现,Fingerprints法已成为数据库中标准的序列分析工具[7],有网络版可使用。当前最新的PRINTS含有1600家族的9800个Motifs[8]。
在这个实验中评估预测Motifs的准确率采用了信息量 IC(Information Content)[9]。
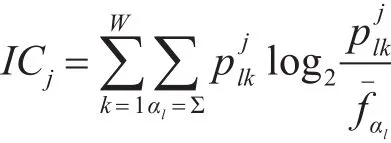
其中表示字符αl在背景序列中出现的频率,IC值越高说明序列越保守,因而可以比较Motifs在不同序列中的数量,实际计算中可通过统计位置权重矩阵得到[10]。
我们选用表1中所列的4个PRINTS蛋白质家族作为测试集,考虑到时间复杂度,选定每个家族的各序列长度在150bp~300bp之间,用Fingerprints法找出在每个成员出现一次的Motifs(即单拷贝序列),再将这些Motifs从数据集中删除。我们设定Motifs的长度为W,采用MEME和PKGE算法发现蛋白质家族中最多有20个Motifs。

表1 PRINTS的蛋白质家族
图2柱状图表示在每条序列中Motifs出现的数量。其中黑色柱状图表示MEME在4个蛋白质家族的预测数量,灰色柱代表PKGE算法预测的Motifs数量,由于所有Motifs在序列中有相同的发生率,因此可以用IC值来比较预测效率[11]。其中MEME的IC值可通过运行软件,统计输出的IC值后求平均值得到,而PKGE算法计算IC值,可通过对PWM矩阵中的序列字符的对应值求平均后得到。设定相同长度为W的Motifs的IC的平均值标记在图2柱状图的上方,试验统计数据表明通过PKGE算法测定的IC值较MEME的要高。
4.2.2 MEME-MAST算法测试[12]
实验目的是通过比较MEME和PKGE算法对蛋白质家族的Motifs预测,得到对目标序列的精确性分析,由于以上的实验结果通过IC值证实我们的算法在发现大量更保守的Motifs时有一定的作用,因此下一步中使用MEME-MAST来预测Motifs。
MEME算法的基本思想是把序列集分成Motifs模式和背景模式,利用EM算法计算出每个字母在短序列中每个位置出现的概率,然后算出该短序列分别出现在Motifs模式和背景模式下的概率,最后通过统计方法确定该短序列是不是一个Motifs;MAST算法是计算数据库中每个序列和给定一组Motifs中每个Motifs的匹配值。对于每个序列,匹配值就是各种不同类型的P值,它们被用来决定序列和Motifs集的匹配度和Motifs大概的顺序以及各个Motifs出现在序列中的间隔[13]。
选取表2所示4个PROSITE蛋白质家族的数据集[14],在每个家族被随机的挑选部分序列(10条)作为Motifs预测的数据集。设定W=10,通过算法去除冗余,表3所示为预测的PROSITE蛋白质家族的Motifs的数量,可以看出PKGE算法识别了大量的Motifs。

图2 PKGE算法与MEME算法预测Motifs比较

表2 PRINTS的蛋白质家族

表3 预测的PROSITE蛋白质家族Motifs数量对比
MEME-MAST算法计算Motifs的目标序列后统计E值,实验方法如下:利用MAST和PKGE算法处理一段序列,在MAST输入一段已知的Motifs并计算每条序列的E值,并将开始目标序列的E值作为阳性分类的依据。
考虑到算法的敏感度和特异性,真阳性的减小降低了敏感度,而假阳性的减小对提高特异度有利。为了提高正确率,需要获得较大的敏感度和较大的特异度,因此选择合适的Motifs长度非常重要,文中选择了如表2所示长度为100bp~360bp的序列。
图3是利用SPSS绘制的算法在四个蛋白质家族数据中执行的ROC曲线,ROC(Receiver Operating Characteristic,接收者工作特征曲线)是利用真阳性和假阳性绘制的曲线[15]。曲线的位置用来判断其所代表算法的优劣,曲线越靠近左上角,或者曲线下方的面积越大,代表算法的分类的精确度越高。从曲线可以清晰看出PKGE算法预测精确度较高。

图3 两种算法预测Motifs的ROC曲线
5 结语
本文采用统计学方法来比较和筛选Motifs预测软件的预测结果,将数据集中已知Motifs作为参考,将Motifs预测算法对数据集的搜索结果作为对数据集中序列的分类。通过测试集来测试Motifs预测算法的精确性。分类效果越好,Motifs模型越能真实反映蛋白质家族的情况。反之,模型就越可能是随机产生的而不具有生物意义。
评价中应用PKGE算法对训练数据集和测试数据集进行了实验,结合同样基于EM算法的MEME算法工具进行了对比实验,应用我们的评测方案在实验中搜集了大量实验参数,无论是在相同长度的Motifs还是在时间复杂度上都较MEME有所优化。通过运用信息量IC等指标对两种算法工具进行了定量检测,最后结合医学检测中常用的ROC曲线进行了特异度和敏感度的比较,进一步验证PKGE算法的改进性。
结合生物实验中总结的经验方法对照通过算法获取的Motifs能够有效地提高预测算法的精确性,筛选后的数据集还需要生物实验来验证才能最终被确定。
本文的评价策略还存在一定的不足,例如本身在一个蛋白质家族的成员序列之间就存在一定的差异,因而通过随机选取的训练集和测试集序列就会有一定的偏差。此外受到实验中软硬件环境的制约,评价策略的效果也会受到一定的影响。因而在后面的研究中还需要对训练集和测试集序列建立更好的数据模型,以提高通过本文评价策略筛选Motifs的精确性。
[1]杜春鹃,朱云平,贺福初,等.蛋白质家族模体(motif)的评价策略[J].北京生物医学工程,2005,24(2):97-102.DU Chunjuan,ZHU Yunping,HE Fuchu,et al.A New Strategy to Evaluate Protein Motifs[J].Beijing Biomedical Engineering,2005,24(2):97-102.
[2]张斐,谭军,谢竞博.基于不同算法的motif预测比较分析与优化[J].计算机工程,2009,35(22):94-96.ZHANG Fei,TAN Jun,XIE Jingbo.Comparison,Analysis and Optimization of Motif Finding Based on Different Algorithms[J].Computer Engineering,2009,35(22):94-96.
[3]TIMOTHY L B,CHARLES E.The value of prior knowledge in discovering Motifs with MEME.Proceeding of the Third International Conference on intelligent Systems for Molecular Biology,Menlo Park,California,1995[C].AAAI Press,1995,3:21-29.
[4]王维彬,钟润添.一种基于贪心EM算法学习GMM的聚类算法[J].计算机仿真,2007,24(2):65-68.WANG Weibin,ZHONG Runtian.A C lustering A lgorithm Based on G reedy EM A lgorithm Learning GMM[J].Computer Simulation,2007,24(2):65-68.
[5]张懿璞.转录因子结合位点识别问题的算法研究[D].西安:西安电子科技大学,2014:120-121.ZHANG Yipu.Algorithm research on the problem of transcription factor binging sites dentification[D].Xi'an:Xidian University,2014:120-121.
[6] T K Attwood,M D R Croning,D R Flower,et al.PRINT-S:the database formerly known as PRINTS[J].Nucleic Acids Res,2000,28:225-227.
[7]杜耀华,倪青山,王正志.利用序列保守模体和局部构象信息预测转录因子结合位点[J].生命科学研究,2006,10(3):215-223.DU Yaohua,NI Qingshan,WANG Zhengzhi.Computerational Prediction of Transcription Factor Binding Sites Based on Conserved Motif and Local Conformational Knowledge in Genomic Sequences[J].Life Science Research,2006,10(3):215-223.
[8]G Pavesi,P Mereghetti,F Zambelli,et al.MoD Tools:regulatory Motif discovery in nucleotide sequences from co-regulated or homologous genes[J].Nucleic Acids Res,2006,34(Web Sever issue):566-570.
[9] T K Attwood,M D R Croning,D R Flower,et al.PRINT-S:the database formerly known as PRINTS[J].Nucleic Acids Res,2000,28:225-227.
[10]王欣.模体的并行聚类算法及在短柄草核心启动子预测的应用研究[D].青岛:青岛大学,2016.WANG Xin.A parallel clustering algorithm for the model body and its application in the prediction of the core Promoter of the short stalks[D].Qingdao:Qingdao University,2016.
[11]刘维,陈汉武,陈崚.一种识别基因调控元件的新型优化算法[J].计算机应用与软件,2013,30(1):21-28.LIU Wei,CHEN Hanwu,CHEN Ling.A Novel Optimisation Algorithm for Gene Regulatorary Elements Recognition[J].Computer Applications and Software,2013,30(1):21-28.
[12]Grundy William N,Bailey TL,Elkan CP,et al.Meta2MEME:Motif2based hidden markov models of biological sequences[J].Computer Applications in the Biosciences,1997,13(4):397-406.
[13]霍红卫,郭丹丹,于强,等.(l,d)-模体识别问题的遗传优化算法[J].计算机学报,2012,35(7):1429-1439.HUO Hongwei,GUO Dandan,YU Qiang,et al.Genetic Optimization for(l,d)-Motif Discovery[J].Chinese Journal of Computers,2012,35(7):1429-1439.
[14]T L Bailey,C Elkan.Unsupervised learning of multiple Motifs in biopolymers using expectation maximization[J].Machine Learning,1995,21:51-83.
[15]R Durbin,S Eddy,A Igogh,et al.生物序列分析,第三章:蛋白质和核酸的概率论模型[M].北京:清华大学出版社,2010.R Durbin,S Eddy,A Igogh,et al.Biological sequence analysis,third chapter:the probability theory model of protein and nucleic acid[M].Beijing:Tsinghua University Press,2010.
