考虑颗粒变形和颗粒间变形的孔隙压缩系数

毛小龙 ，刘月田 ，关文龙 ，刘思平 ，李骏

（1.中国石油大学（北京）油气资源与探测国家重点实验室，北京 102249；2.中国石油勘探开发研究院，北京 100083）

0 引言

岩石孔隙压缩系数是油藏工程研究的基础物性参数，在油藏弹性产能评价、动态地质储量计算以及储层应力敏感程度评价等方面都有非常重要的作用［1-17］。然而，由于技术条件的限制，例如岩心与封套之间存在一定的微间隙，实验室体积法直接测试孔隙压缩系数过程中易产生一定误差。相关研究提出的理论计算方法不统一［1-10］，得到了一些相互矛盾的认识：李传亮［1-4］认为孔隙压缩系数小于颗粒平均压缩系数，与孔隙度正相关，传统体积法测试结果（Hall图版［5］）偏高；王历强［6］则认为孔隙压缩系数大于颗粒平均压缩系数；张津宁［7-10］等则认为体积法测试不存在数量级别的偏差，孔隙压缩系数与孔隙度负相关。这给孔隙压缩系数的测试和计算造成了困惑，对油藏工程研究和评价十分不利。因此，理清岩石孔隙体积应力应变机理，并建立一种全面可靠的孔隙压缩系数理论计算方法十分必要。

关于多孔介质的变形机理，传统Terzaghi有效应力原理考虑了土颗粒间滑动变形，而适用于岩石的Skempton有效应力方程则综合考虑了颗粒变形（又称为本体变形）和颗粒间滑动变形（又称为结构变形）。本文将从Terzaghi及Skempton 2个经典有效应力原理分析出发，综合考虑岩石颗粒变形和颗粒间变形机理，利用2种方法推导出岩石表观体积、基质颗粒体积、孔隙体积随孔隙流体压力变化的关系式，建立精确计算孔隙压缩系数的关系式，分析其变化规律并进行实例验证。

1 经典有效应力理论分析

Terzaghi于1923年提出了有效应力概念，1936年给出了Terzaghi有效应力表达式：

式中：σeff为有效应力，MPa；σ 为总应力，MPa；p 为孔隙流体压力，MPa。

Terzaghi有效应力原理可以归纳为两方面：土体体积变形和抗剪切强度完全取决于有效应力；有效应力等于总应力减去孔隙流体压力。其假设条件为土颗粒不可压缩，土体受压变形完全由颗粒间滑动引起。

与松散土体不同，储层岩石是固结的，这导致许多研究对于岩石的颗粒变形和颗粒间滑动变形相对大小认识不清。在计算岩石孔隙体积变化时，一些研究直接引用Terzaghi有效应力原理，只计算了颗粒间滑动变形的影响；而另外一些研究者则只计算了颗粒体积变形的影响，以文献［1-3］的理论推导较为典型：

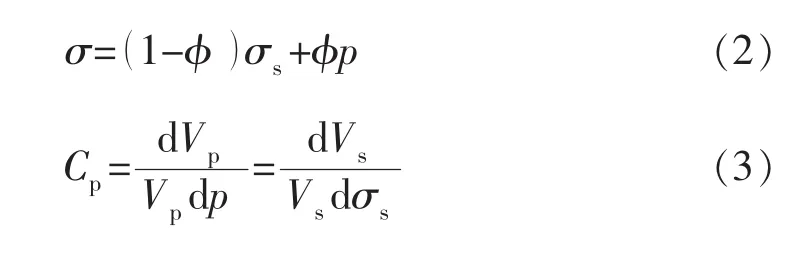
式中：σs为基质颗粒应力，MPa；φ 为孔隙度；Cs，Cp分别为基质颗粒压缩系数、孔隙压缩系数，MPa-1；Vs，Vp分别为基质颗粒体积、孔隙体积，m3。

据统计，岩石压缩系数多为颗粒压缩系数的2～25倍，表明多数岩石的颗粒变形和颗粒间滑动变形均不可忽略。适用于岩石表观体积变形，并综合考虑了颗粒变形和颗粒间变形的Skempton有效应力原理，可以较为精确地计算岩石外观体积应变εb：

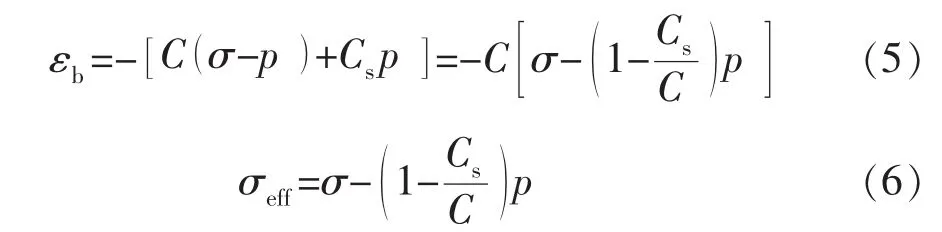
式中：C为岩土净应力作用下表观体积压缩系数，MPa-1。

总表观体积应变为净应力引起的表观体积应变与孔隙流体压力引起的表观体积应变之和。恒总应力Δσ=0时，储层岩石表观体积应变为

需要说明的是，Skempton有效应力方程只适用于计算岩石表观体积应变，要计算岩石孔隙体积应力应变及孔隙压缩系数，需要在考虑颗粒变形和颗粒间变形基础上进一步计算。

2 孔隙压缩系数新关系式推导

2.1 方法一

总应力恒定、流压变化时，根据Skempton有效应力原理（式（7）），表观体积变化量 ΔVb为

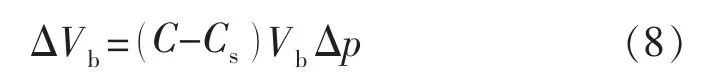
式中：Vb为岩石表观体积，m3。

引起基质颗粒体积变形的基质颗粒应力σs，以平均横截面作受力平衡分析，由式（2）得：

恒总应力Δσ=0时，颗粒体积变化量ΔVs为

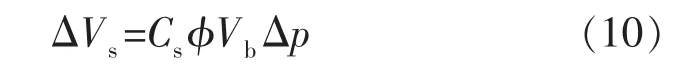
对应的孔隙体积变化量ΔVp为

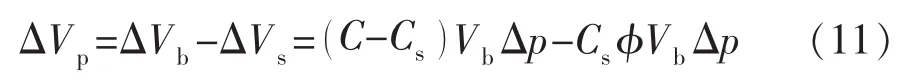
孔隙压缩系数为

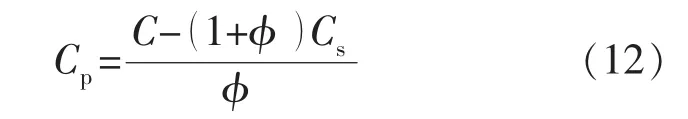
据统计和岩石物理学基本理论可知，常见岩石C为Cs的2～25倍，C＞（1+φ）Cs恒成立，孔隙压缩系数大于0。新关系式考虑了颗粒变形和颗粒间变形的综合效果，但上述新关系式推导中仍未能区分颗粒变形和颗粒间变形分别对岩石孔隙压缩系数有多大影响。

2.2 方法二

区分颗粒变形和颗粒间变形比较复杂，颗粒变形是净应力和孔隙流压共同作用的结果，颗粒间变形完全由净应力引起，净应力表观体积压缩系数中包括了由净应力引起的颗粒变形和颗粒间变形两部分。将引起颗粒变形的作用力分为净应力和流压两部分：

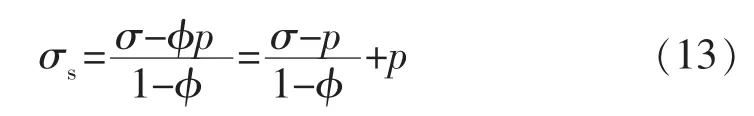
颗粒变形的净应力作用部分是（σ-p）/（1-φ），流压作用部分为p，这样看似简单区分其实具有物理意义。颗粒平均受力面积为（1-φ）A，净应力作用部分的物理意义是除去流压作用部分的颗粒间作用力在单位基质颗粒面积上的作用力；流压作用部分p为孔隙流压对颗粒的中性压缩作用力。

恒总应力条件下，由净应力引起的颗粒体积变化量 ΔVs σnet为

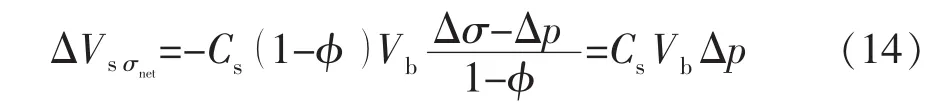
对应的净应力颗粒变形引起的表观体积变化量ΔVb σnet为

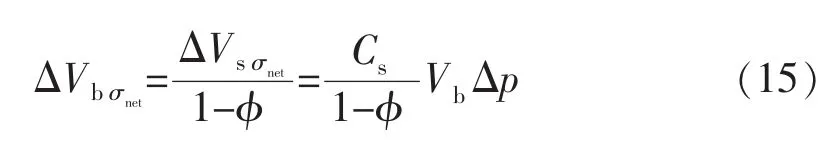
净应力颗粒间变形引起的表观体积变化量ΔVbσij为

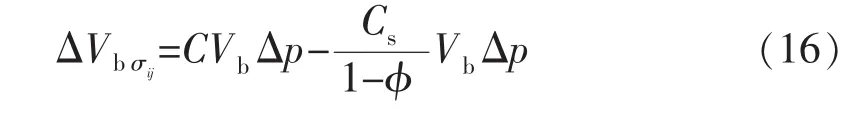
颗粒间变形完全由净应力引起，且颗粒间变形不引起颗粒体积变形，因此颗粒间变形引起的孔隙体积变化量ΔVpσij等于对应的表观体积变化量。

颗粒间变形孔隙压缩系数Cpσij为

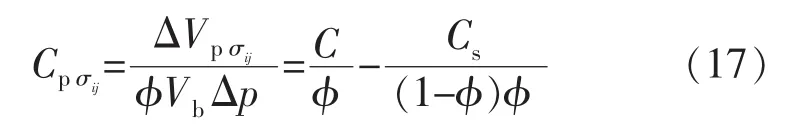
颗粒变形由净应力和流压共同作用引起，由式（10），（13）可知，恒总应力 Δσ=0，颗粒变形引起的孔隙体积变化 ΔVpσs为

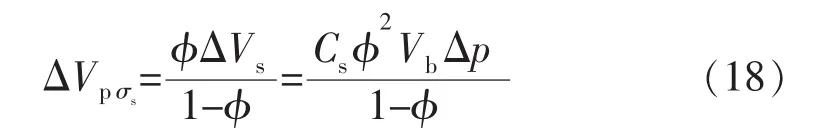
颗粒变形导致的孔隙压缩系数Cpσs为

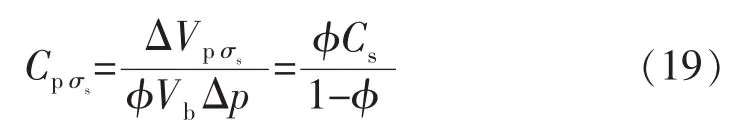
这一结果与文献［1-3］认识一致。

颗粒间变形和颗粒变形引起的总孔隙体积变化为

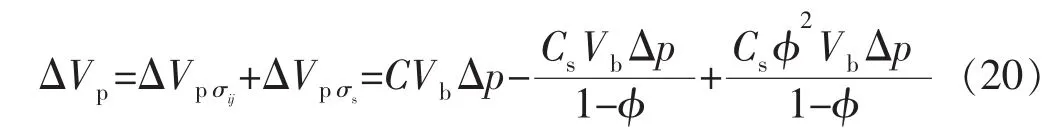
对应的总孔隙压缩系数为

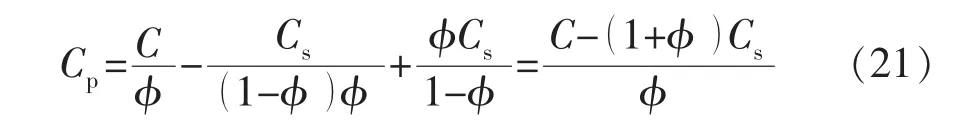
这与Skempton有效应力原理直接推导得到的孔隙压缩系数完全一样，2种方法论证了综合考虑颗粒间变形和颗粒变形得到的孔隙压缩系数新关系式的正确性。

3 孔隙压缩系数变化规律分析

由上述2种推导方法可以得出，孔隙压缩系数新关系式为

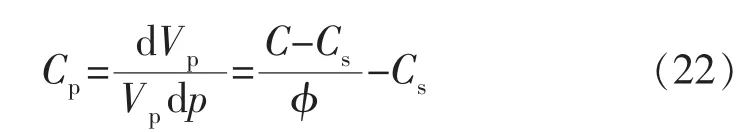
可以看出，孔隙压缩系数与孔隙度负相关。从孔隙压缩系数的定义也可得出：随着孔隙度减小，孔隙体积减小，分子受dVp/dp压缩，减小的速度越来越慢，小于孔隙体积稳定下降的速度，整体上Cp与孔隙度负相关。这与文献［1-3］中孔隙压缩系数变化规律不同，与实验测试得到的Hall图版曲线（见图1）［5］规律一致。Hall图版的孔隙压缩系数规律为

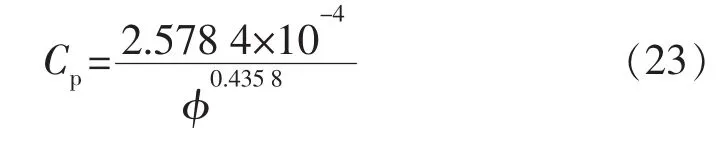
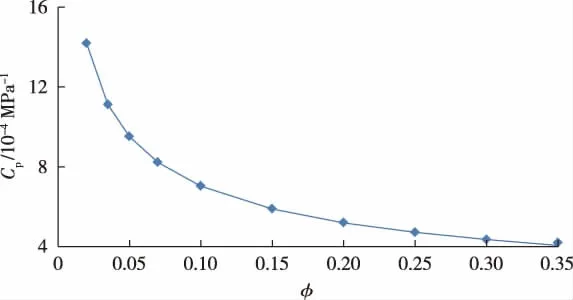
图1 Hall图版曲线

根据Hall图版和相关文献孔隙压缩系数测试值可知［5，8-10］，常见储层岩石的孔隙压缩系数为 10-4～10-3MPa-1。而常见矿物颗粒的压缩系数为10-6～10-5MPa-1，常见岩石的表观体积压缩系数10-5～10-4MPa-1。利用孔隙压缩系数新关系式（22），孔隙度取 0.02～0.35，计算得到取值范围也在10-4～10-3MPa-1，符合实验测试和Hall图版的取值范围。这说明理论计算和Hall实验测试不存在数量级别的误差，储层岩石满足孔隙压缩系数远大于岩石表观压缩系数，岩石表观压缩系数大于基质颗粒压缩系数。

4 应用实例

以3块岩石为例，岩块1为粉砂岩，孔隙度为0.048，岩石表观体积压缩系数为7.41×10-5MPa-1；岩块2为Berea砂岩，孔隙度为0.160，岩石表观体积压缩系数为11.96×10-5MPa-1；岩块3为高孔高渗砂岩，孔隙度为0.250，岩石表观体积压缩系数为15.22×10-5MPa-1。3块岩石矿物颗粒压缩系数都取2.70×10-5MPa-1。岩石表观体积压缩系数和矿物颗粒体积压缩系数均可通过弹性模量法测得。

1）采用孔隙压缩系数新关系式（22），代入计算得到岩块1、岩块2、岩块3的孔隙压缩系数分别为9.54×10-4，5.52×10-4，4.74×10-4MPa-1； 与 3 块岩石的实验测试孔隙压缩系数值 9.68×10-4，5.73×10-4，4.72×10-4MPa-1相近，且与孔隙度呈负相关关系。理论计算和实验测试结果相互验证，说明得到的孔隙压缩系数较为可靠，误差较小。

2）采用式（17）进一步计算得到，3块岩石颗粒间变形引起的孔隙压缩体积系数分别为9.53×10-4，5.47×10-4，4.65×10-4MPa-1；采用式（19）计算得到，3 块岩石颗粒变形引起的孔隙压缩系数分别为1.36×10-6，5.14×10-6，9.00×10-6MPa-1。

3）计算可知：3块岩石的颗粒间变形引起的孔隙压缩系数均远大于颗粒变形引起的孔隙压缩系数，忽略颗粒间变形会导致孔隙压缩系数计算值远低于实际值；而忽略颗粒变形，即假设Cs=0，式（22）退化为Cp=C/φ，代入计算得到3块岩石孔隙压缩系数分别为15.44×10-4，7.45×10-4，6.08×10-4MPa-1， 与实测值 9.68×10-4，5.73×10-4，4.72×10-4MPa-1相比偏大。 因此颗粒变形和颗粒间变形都得考虑。

5 结论

1）传统Terzaghi有效应力原理适用于土体体积应力应变，不适用于岩石孔隙压缩系数和对应的渗透率应力敏感研究。

2）颗粒间变形引起的孔隙压缩系数远大于颗粒变形引起的孔隙压缩系数，忽略颗粒间变形会使孔隙压缩系数计算值远低于实际值，忽略颗粒变形则使得孔隙压缩系数计算值偏大。

3）综合考虑颗粒变形和颗粒间变形，以2种方法理论推导建立了孔隙压缩系数的精确计算关系式，新关系式与岩石力学理论体系以及Hall实验测试图版反映的规律一致。

4）多数岩石孔隙压缩系数远大于表观体积压缩系数，表观体积压缩系数大于颗粒压缩系数。“高孔高压缩、低孔低压缩”适用于表观体积压缩系数，孔隙压缩系数则由于孔隙体积自身是分母，与孔隙度负相关。

［1］李传亮.岩石压缩系数与孔隙度的关系［J］.中国海上油气（地质），2003，17（5）：355-358.

［2］李传亮.再谈岩石的压缩系数：回应高有瑞博士［J］.中国海上油气，2011，25（4）：85-87.

［3］李传亮.再谈岩石的压缩系数：回应王厉强博士［J］.新疆石油地质，2012，33（1）：125-127.

［4］李传亮.实测岩石压缩系数偏高的原因分析［J］.大庆石油地质与开发，2005，24（5）：53-54.

［5］HALL H N.Compressibility of reservoir rocks［J］.Journal of Petroleum Technology，1953，5（1）：17-19.

［6］王厉强，李正科，袁昭，等.实测岩石孔隙压缩系数偏高原因再分析：与李传亮教授商榷［J］.新疆石油地质，2012，33（3）：379-381.

［7］张津宁，张金功.柴西地区变围压条件下储层物性变化规律［J］.特种油气藏，2016，23（5）：114-118

［8］高有瑞，刘艳，时付更.基质型灰岩储层岩石压缩系数的确定［J］.中国海上油气，2011，23（4）：247-250.

［9］罗瑞兰.关于低渗致密储层岩石的应力敏感问题：与李传亮教授探讨［J］.石油钻采工艺，2010，32（2）：126-130.

［10］任勇，孙艾茵.岩石弹性变形中孔隙度变化的研究［J］.新疆石油地质，2005，26（3）：336-338.

［11］TERZAGHI K.Die berechnung der curchlassigkeitziffer des tones aus dem verlauf der hydrodynamischen spannungserscheinumgen ［J］.Sber Akad Wiss Wien，1923，132（3）：125-138.

［12］曹廷宽，刘成川，曾焱，等.基于CT扫描的低渗砂岩分形特征及孔渗参数预测［J］.断块油气田，2017，24（5）：657-661.

［13］XUHF，XIE K H.Effective stress in soils under different saturation conditions［J］.Journal of Central South University of Technology，2011，18（6）：2137-2142.

［14］李传亮，孔祥言，徐献之.胶结多孔介质的双重有效应力［J］.自然杂志，1999，21（5）：288-292.

［15］李海鹏，王道串，李蒋军，等.储层岩石压缩系数的一种预测方法［J］.断块油气田，2009，16（1）：45-47.

［16］聂法健，田巍，国殿斌，等.深层高压低渗透储层应力敏感性研究［J］.断块油气田，2016，23（6）：788-792.

［17］张玲，魏绍蕾，黄学斌，等.基于综合权重法的页岩气储量评价方法探讨［J］.实验石油地质，2017，39（5）：694-699.