基于VPG白噪声滤波模型在四轴车体系统驾驶室的平顺性研究

陈 宁， 张功学

(陕西科技大学 机电工程学院， 陕西 西安 710021)

0 引言

随着社会经济持续发展，交通运输业中公路运输业将长期繁荣.多轴重型汽车半挂车列车成为大宗物品运输的主要交通工具.但在运输过程中存在因路面不平冲击作用下而引发重卡系统发生整体的振动导致运输事故的持续发生.如果整个系统长期处于这种状态，轻者会影响被运输货物的安全性及车辆的使用寿命，重者将会对人体造成较大伤害而出现一系列社会事故.因此对于重卡系统的动力学模型研究十分必要.针对上述问题，在此应用某款[1]国产四轴重型汽车半挂车列车部分参数为例，建立相应的整车动力学模型，由于篇幅将其空间模型通过微幅振动条件约束转化为平面动力学模型，若深究三维模型，可沿其二维模型方法推算，在此不加以赘述.

关于此类课题，众多国内外学者[2-6]对其展开研究，以下为部分学者的研究现状：Cole等[7]、Vaduri等[8]国内外学者对于二轴牵引半挂车开展过相关动力学方面的研究，并假设了不同的研究对象，针对整车系统的各自由度建立动力学方程.二轴牵引半挂车相对其他多轴牵引半挂重卡结构较为简单且不涉及超静定问题，求解较为简单，运用常规静力学手段就可进行求解.Velmurugan等[9]和李杰等[10]对于多轴整车及牵引半挂车开展过相关动力学研究，并取得了系列成果.在对1/4或者1/2车体展开研究通常采用AR模型法、滤波白噪声法和小波包分析等方法[11-15]，对整车建立动力学模型后结合相关实测路段的激励并加以相应标准路面归纳进行求解相关研究课题较少，所以以四轴重型汽车半挂车列车为例作为多轴重卡样本展开相关研究，具有较强的实践性研究价值.

1 整车系统的空间动力学模型

四轴重卡半挂列车的参数化动力学模型主要由两大车体和零部件组合组成，在参数简化的过程中主要是根据整车模型各部分主要起缓冲的振动特性的零件为支撑，并将其转化为具体的动力学的简易模型.四轴重卡半挂列车主体部分两轴牵引车、两轴半挂车和驾驶室相组合而成，其中鞍座将两轴牵引车和两轴半挂车连接起来，驾驶室悬架将两轴牵引车和驾驶室相连接起来.整车具体包括部分有：驾驶室一个、正副驾驶室人员两名、座椅两个、驾驶室悬架四副、车架一个、前轴一根、前排非独立悬架一副、后轴一根、后排非独立悬架一副、前后轴轮胎两对、两轴半挂车架一个、车轴三根、非独立悬架两副和挂车轮胎两对.根据实车在不同的路况下运行的状态不同，简化车辆不必要的部分后，关于四轴重卡半挂列车做如下具体的假设：

(1)列车在运行过程中基于车辆在平衡位置做微小的振幅运动，而且排除变速运动；

(2)模型中所有的人体、车架、两轴半挂车架、驾驶室和驾驶室均假设为刚体，不考虑其弹性刚度和阻尼性质，其中座椅关于车体纵向中轴面对称；

(3)模型中所有的座椅、所有的悬架、悬置和鞍座简化为无质量的弹簧和阻尼器，并且弹簧和阻尼器相并联，其中所有悬架关于车体纵向中轴面对称；

(4)模型中所有的轮胎与路面的接触均为点接触，源于路面的激励只作用于接触点上过实际轮胎的圆心垂直向上；

(5)模型中所有轮胎简化为无质量的弹簧；

(6)模型中所有简化后的弹簧满足胡克定律中弹力和弹簧伸缩位移呈线性的要求；

(7)模型中将人员和座椅简化为统一的刚体，不单独区分；

(8)模型中所有简化后的阻尼器满足阻尼力由速度的变化而呈现线性改变.

对建模的假设条件的误差分析说明如下：

(1)车辆微小的振幅运动是车辆系统动力学仿真类研究的基础假设，目的是为了排除车路分离的情况出现，若非微幅振动，就可能出现车路分离的情况继而出现时域的不连续性，同时导致路面无法对机械系统进行激励的情况出现.会出现系统振动响应和路面激励频谱无法对应，失真的现象发生.

(2)抓住主要矛盾，忽略次要矛盾.严格来说，人体、车架、两轴半挂车架和驾驶室都是有弹性刚度和阻尼性质的，但这里统一忽略是基于两点原因：①非主要研究的对象，例如人体，严格来说要考虑人的皮肤、皮下脂肪层和韧带等也有刚度阻尼系数，但对于本课题的研究对象没有必要考虑.②刚度太小，对整车的系统力学几乎没有影响，例如车架，一般大型车辆的车架都是铸铁铸造，高度太小，没有必要考虑.

(3)因为座椅、悬架悬置和鞍座的特点是质量很小，特别是相对于气压主要部件(比如车架、驾驶室等)质量很小，故在整体的动力学方程建立中，其质量因素可以忽略.但是这些部件的刚度和阻尼系数却相对较大.对于所有悬架关于车体纵向中轴面对称目的是忽略一些零件的质量和形态的不均性(比如悬架)，是通用的车辆动力学研究假设.

(4)忽略车在较大的情况下出现的轮胎与路面出现线接触的情况，因为在实测情况下都是点测试，否则会减小轮胎激励的灵敏度或检测不到信号，是常规的理想实验假设.

(5)忽略次要条件，抓住主要性质.是车辆类系统动力学的常规假设，也有人考虑轮胎阻尼和质量.虽然会增加仿真精度，但会大幅增大计算量，尤其是对于这种大型多激励车体而言.

(6)因为在一些新式车辆采用了锥形弹簧等非线性部件进行减振，该假设是为加强仿真的严谨性.

(7)将人和座椅简化为统一的刚体，不单独区分也是对于排除在振动较大的情况下出现人体和座椅出现分离不接触的现象，为研究平顺性提供连续性，为车辆系统常规性假设.

(8)同刚度和位移的关系呈现线性改变，同理，力学近似处理.

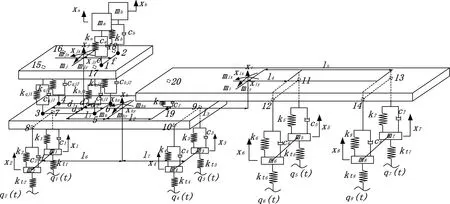
图1 四轴重卡半挂列车的空间动力学模型

图1是为研究整车结构建立的空间三维动力学模型，具体变量如图标注所示.相对空间整车模型，多数四轴重卡半挂列车基本满足车体关于纵向的轴对称面呈对称的特性，重型汽车列车的测试通常在相对平坦路面上进行模拟激励仿真，空间整车结构模型通过下述限定条件转换化为1/2整车模型.

(1)研究对象关于中心轴对称面对称，不考虑前置发动机等零部件的不均匀位置而导致牵引车的质量不均，故而忽略驾驶室质心到悬置节点34、56、35、46的相对距离，即d1=d2和d3=d4；

(2)由于重型汽车通常都为非独立悬架以及常用测试路面相对平坦，故而忽略同轴间的车轮收到激励振动的相干性，忽略空间范围的轴向的受力状态，即忽略x轴向的影响，忽略其他振动；

(3)设定人员a和座椅a的质量等同于人员b和座椅b的质量,同时座椅a和座椅b弹性刚度和阻尼系数相同.

整车动力学模型的建立及设定的条件下，对于四轴重卡半挂列车的参数化动力学模型的各参数说明，为后续建模的参数及变量进行限定.针对四轴重卡半挂列车的平面动力学模型进行的参数化说明图2所示.

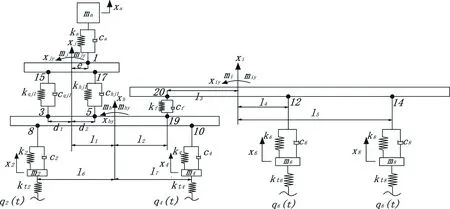
图2 四轴重卡半挂列车的空间动力学模型

图2中：ma、mb—人员a、b和座椅a、b的质量，kg；mj—驾驶室的质量，kg；mjx、mjy—驾驶室绕其质心的俯仰、测斜转动惯量，kg·m2；mh—牵引车架质量，kg；mhx、mhy—牵引车绕其质心的俯仰、测斜转动惯量，kg·m2；mi—半挂车的质量，kg；mix、miy—半挂车绕其质心的俯仰、测斜转动惯量，kg·m2；m1、m2、m3、m4—牵引车前轴、后轴的非簧载质量，kg；m5、m6、m7、m8—半挂车前轴、后轴的非簧载质量，kg；ca、cb—座椅a、b的垂直阻尼系数，N·s/m；cqj1、cqj2、chj1、chj2—牵引车和驾驶室间前、后悬置垂直阻尼系数，N·s/m；cf—鞍座的垂直阻尼系数，N·s/m；c1、c2、c3、c4—牵引车前轴、后轴的垂直阻尼系数，N·s/m；c5、c6、c7、c8—半挂车前轴、后轴的垂直阻尼系数，N·s/m；ka、kb—座椅a、b的垂直刚度系数，N/m；kqj1、kqj2、khj1、khj2—牵引车和驾驶室间前、后悬置垂直刚度系数，N/m；k1、k2、k3、k4—牵引车前轴、后轴的垂直刚度系数，N/m；k5、k6、k7、k8—半挂车前轴、后轴的垂直刚度系数，N/m；kf—鞍座的刚度系数，N/m；e—座椅到驾驶室质心的纵向距离，m；f—座椅a到座椅b的纵向距离，m；d—同轴悬架间的距离，m；d1、d2、d3、d4—驾驶室质心到悬置节点34、56、35、46的距离，m；l1—驾驶室质心到牵引车架质心间的距离，m；l2—牵引车架质心到鞍座质心的距离，m；l3—鞍座质心到半挂车车架质心的距离，m；l4、l5—半挂车车架质心到半挂车前、后轴质心的距离，m；l6、l7—牵引车架质心到牵引车前、后轴质心的距离，m；xa、xb—人员a、b和座椅a、b的垂直位移，m；xj—驾驶室的垂直位移，m；xjx、xjy—驾驶室绕其质心处的横向与纵向角位移，rad；xh—牵引车车架质心处的垂直位移，m；xhx、xhy—牵引车车架绕其质心处的横向与纵向角位移，rad；xi—半挂车车架质心处的垂直位移，m；xix、xiy—半挂车车架绕其质心处的横向与纵向角位移，rad；x1、x2、x3、x4—牵引车前、后轴两端非簧载质量的垂直位移，m；x5、x6、x7、x8—半挂车前、后轴两端非簧载的垂直位移，m；q1、q2、q3、q4—牵引车前、后轴两端受位移激励，m；q5、q6、q7、q8—半挂车前、后轴两端受位移激励，m.

2 系统的动力学方程

根据动力学模型以及选择能量法为研究手段，故整车空间模型动力学主要包括三种能量，分别为动能、势能和耗散能，以下列出整车动力学公式.分别为公式(1)、(2)和(3).

整车的动能为：

(1)

整车的耗散能为：

(2)

整车的势能为：

(3)

根据动力学模型以及选择能量法为研究方法，1/2整车模型包括三种能量，分别为动能、势能和耗散能，分别为公式(4)、(5)和(6).

整车的动能为：

(4)

整车的耗散能为：

(5)

整车的势能为：

(6)

简化后三个式子在系统模型仅分析微小平面内的振动而忽略其同轴的影响.因为市场上绝大多数重卡列车都属于非独立悬架，这种简化过程满足具体情况.排除了对于在微小振动发生时，对车辆振动模型影响不大的变量，减少非主要因素,加快了设计效率，有利于求解.

引入路面激励向量{q}，如式(7)所示.

{q}={0 0 0 0 0q2q40 0q6q8}T

(7)

对于向量{x}中的每个量建立相对应的拉格朗日方程，之前需要针对向量{x}定义广义坐标，设其向量{x}中的每个元素的广义坐标为x0.对于每个元素的拉格朗日方程具体如下所示.

(8)

对式(4)、(5)和(6)经求导整理为经典动力学表达形式，具体如式(9)所示：

(9)

式(9)中：[m]—质量矩阵，kg；[c]—阻尼矩阵，kg；[k]—刚度矩阵，N·s/m；[kq]—路面激励矩阵，N/m.

质量矩阵具体表达如下所示：

阻尼矩阵具体表达如下所示：

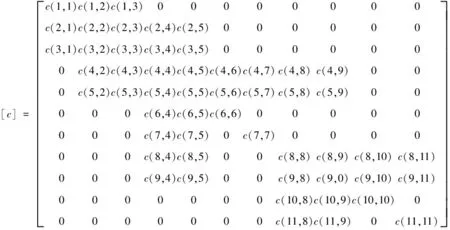
刚度矩阵具体表达如下所示：

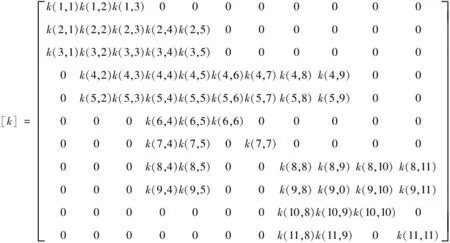
对于上阻尼矩阵各坐标表达式如下所示：

c(2,1)=-ca;

c(3,1)=-eca,c(3,2)=eca-d1cqj1+d2chj1;

c(4,2)=-(cqj1+chj1),c(4,3)=d1cqj1-d2chj1;

c(5,2)=(l1+d1)cqj1+(l1-d2)chj1;

c(5,3)=d2(l1-d2)chj1-d1(l1+d1)cqj1;

c(5,4)=-(l1+d1)cqj1-(l1-d2)chj1-l6c2+l7c4+l2cf;

c(6,4)=-c2,c(6,5)=l6c2;

c(7,4)=-c4,c(7,5)=-l7c4;

c(8,4)=-cf,c(8,5)=-l2cf;

c(9,4)=l3cf,c(9,5)=l2l3cf,c(9,8)=-l3cf+l4c6+l5c8;

c(10,8)=-c6,c(10,9)=-l4c6;

c(11,8)=-c8,c(11,9)=-l5c8;

c(1,1)=ca,c(1,2)=-ca,c(1,3)=-eca;

c(2,2)=ca+cqj1+chj1,c(2,3)=eca-d1cqj1+d2chj1;

c(2,4)=-(cqj1+chj1),c(2,5)=(l1+d1)cqj1+(l1-d2)chj1;

c(3,3)=e2ca+d12cqj1+d22chj1,c(3,4)=d1cqj1-d2chj1;

c(3,5)=d2(l1-d2)chj1-d1(l1+d1)cqj1;

c(4,4)=cqj1+chj1+c2+c4+cf;

c(4,5)=-(l1+d1)cqj1-(l1-d1)chj1-l6c2+l7c4+l2cf;

c(4,6)=-c2,c(4,7)=-c4,c(4,8)=-cf,c(4,9)=l3cf;

c(5,5)=(l1+d1)2cqj1+(l1-d2)2chj1+l62c2+l72c4+l22lf;

c(5,6)=l6c2,c(5,7)=-l7c4,c(5,8)=-l2cf,c(5,9)=l2l3cf;

c(6,6)=c2;

c(7,7)=c4;

c(8,8)=cf+c6+c8;c(8,9)=-l3cf+l4c6+l5c8;

c(8,10)=-c6,c(8,11)=-c8;

c(9,9)=l32cf+l42c6+l52c8,c(9,10)=-l4c6,c(9,11)=-l5c8;

c(10,10)=c6;

c(11,11)=c8;

k(2,1)=-ka;

k(3,1)=-eka,k(3,2)=eka-d1kqj1+d2khj1;

k(4,2)=-(kqj1+khj1),k(4,3)=d1kqj1-d2khj1;

k(5,2)=(l1+d1)kqj1+(l1-d2)khj1;

k(5,3)=d2(l1-d2)khj1-d1(l1+d1)kqj1;

k(5,4)=-(l1+d1)kqj1-(l1-d2)khj1-l6k2+l7k4+l2kf;

k(6,4)=-k2,k(6,5)=l6k2;

k(7,4)=-k4,k(7,5)=-l7k4;

k(8,4)=-kf,k(8,5)=-l2kf;

k(9,4)=l3kf,k(9,5)=l2l3kf,k(9,8)=-l3kf+l4k6+l5k8;

k(10,8)=-k6,k(10,9)=-l4k6;

k(11,8)=-k8,k(11,9)=-l5k8;

k(1,1)=ka,k(1,2)=-ka,k(1,3)=-eka;

k(2,2)=ka+kqj1+khj1,k(2,3)=eka-d1kqj1+d2khj1;

k(2,4)=-(kqj1+khj1),k(2,5)=(l1+d1)kqj1+(l1-d2)khj1;

k(3,3)=e2ka+d12kqj1+d22khj1,k(3,4)=d1kqj1-d2khj1,

k(3,5)=d2(l1-d2)khj1-d1(l1+d1)kqj1;

k(4,4)=kqj1+khj1+k2+k4+kf,

k(4,5)=-(l1+d1)kqj1-(l1-d2)khj1-l6k2+l7k4+l2kf,

k(4,6)=-k2,k(4,7)=-k4,k(4,8)=-kf,k(4,9)=l3kf;

k(5,5)=(l1+d1)2kqj1+(l1-d2)2khj1+l62k2+l72k4+l22kf,

k(5,6)=l6k2,k(5,7)=-l7k4,k(5,8)=-l2kf,k(5,9)=l2l3kf;

k(6,6)=k2+kt2;

k(7,7)=k4+kt4;

k(8,8)=kf+k6+k8;k(8,9)=-l3kf+l4k6+l5k8,

k(8,10)=-k6,k(8,11)=-k8;

k(9,9)=l32kf+l42k6+l52k8,k(9,10)=-l4k6,k(9,11)=-l5k8;

k(10,10)=k6+kt6;

k(11,11)=k8+kt8.

3 路面不平度等级匹配

通过国际标准化组织所制定的ISO/TC108/SC2N67和长春汽车研究所的GB7031——2005《车辆振动输入路面平度表示方法标准》都明确地建议通过使用路面功率谱密度来描述路面不平度，具体表达式如式(10)所示.

(10)

式(10)中：n0=0.1 m-1；Gq(n)—路面空间功率谱密度；n—空间频率；Gq(n0)—路面不平度系数；W—频率指数.

(11)

式(11)中：f=nu；Gq(f)—路面时间功率谱密度；f—时间频率；u—车辆速度.

(12)

式(12)中：σq—均方根；T—运行总时间.

通过式(12)在ISO/TC108/SC2N67和GB7031——2005中，将路面的不平度进行了八个等级的划分，其划分原理为是路面空间功率谱密度，并给出了与各路面相应的均方根大小的值.

通过式(5)可知，当n趋近于0时，Gq(n0)则趋近于无穷，根据现实情况这是不可能的，故而需要对于n的取值进行范围限制.引入空间截止频率nq，从而可将W=2代入公式(10)和(11)，分别变化为式(13)和(14)：

(13)

(14)

通过相关资料可知当nq=0.000 1 m-1时将会使其路面不平度的空间功率谱密度与标准形式的均方根相基本吻合.

在选取适当的路面等级以及何时的车速这两个因素对于整车的仿真很重要，否则仿真结果就有很大偏差.通过MATLAB对于八个等级的路面以及从10～100 km/h进行了白噪声的路面不平度与时间的仿真，在仿真前，对于非主要因素进行了限定，其具体如图3所示.图4为某段路面的实测频谱图，图5为该模型所有车轴所受的激励频谱.

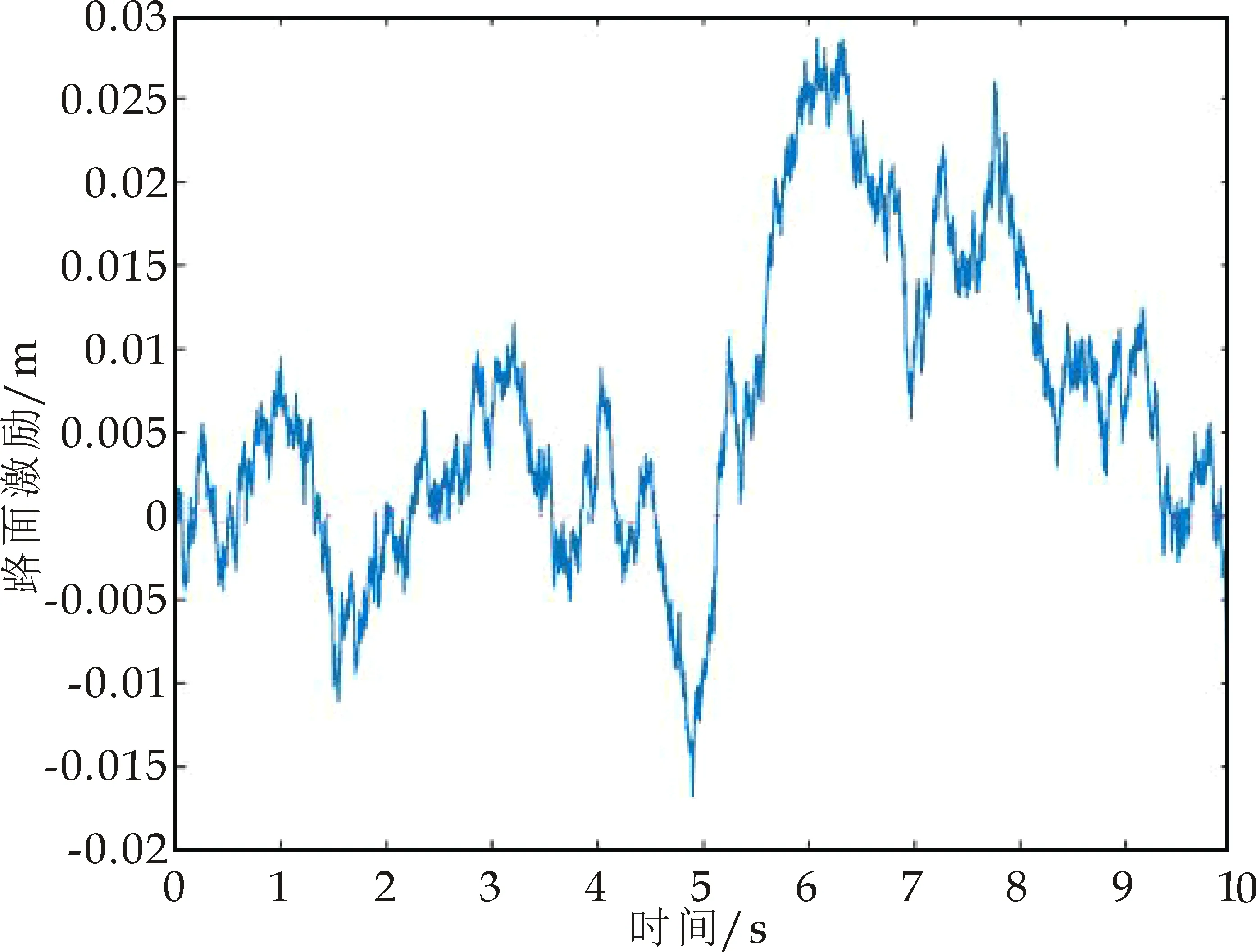
图3 滤波白噪声产生路面频谱图(D级路面20 km/h)

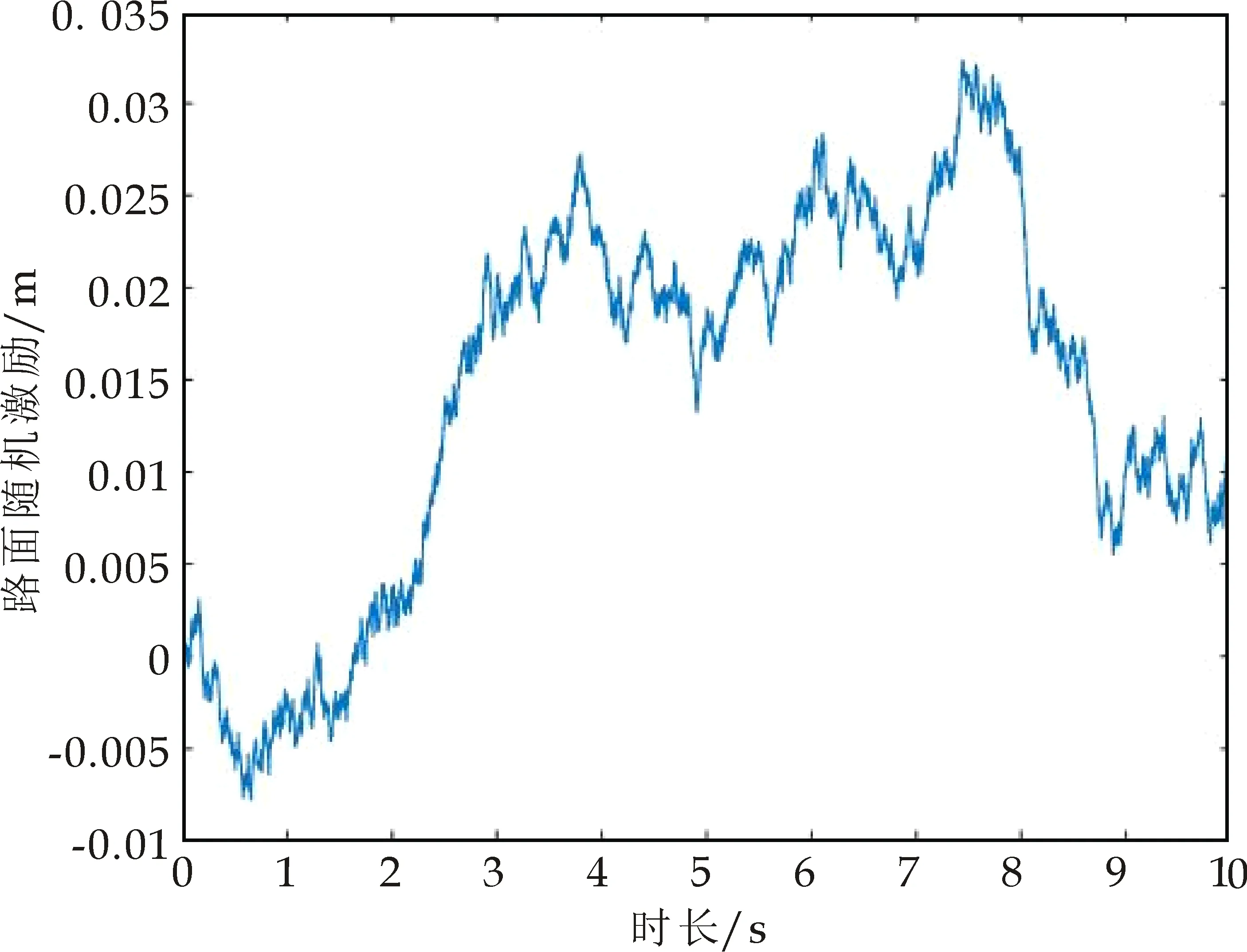
图4 前轮所受某段实测路面频谱图

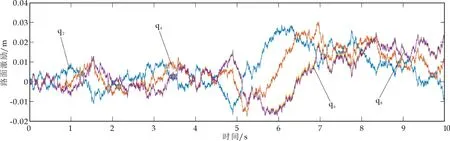
图5 滤波白噪声法模拟四轴所受激励路面频谱

以D级路面为假设路段，则在不同速度下,其PSD路面激励与标准频域的关系如下：通过Base-PSD基频，在频域和时域两种情况下进行对比.可以匹配任意激励对应八个路面等级，但是这种路面等级匹配并非唯一，还要与车辆的具体行驶速度相关联.如果速度可变，则匹配的相应等级不同；同理，如果速度固定，则等级变化程度可成为变量去改变Base-PSD的匹配.采用图4实测频谱的校核方法，选择图5进行工况等级验证，其校核结果如图6所示.

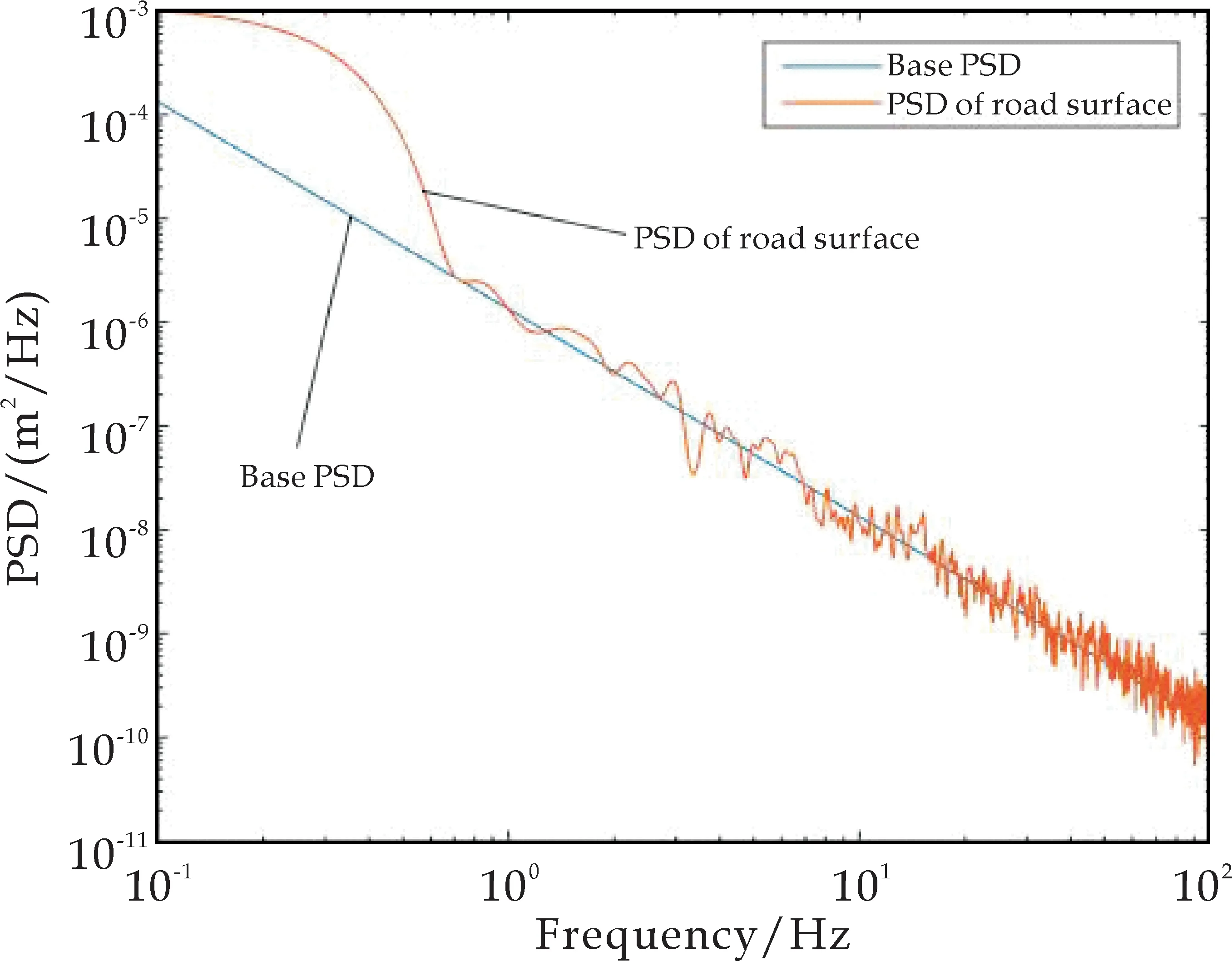
(a)标准路面和逆变换的时间频率功率谱

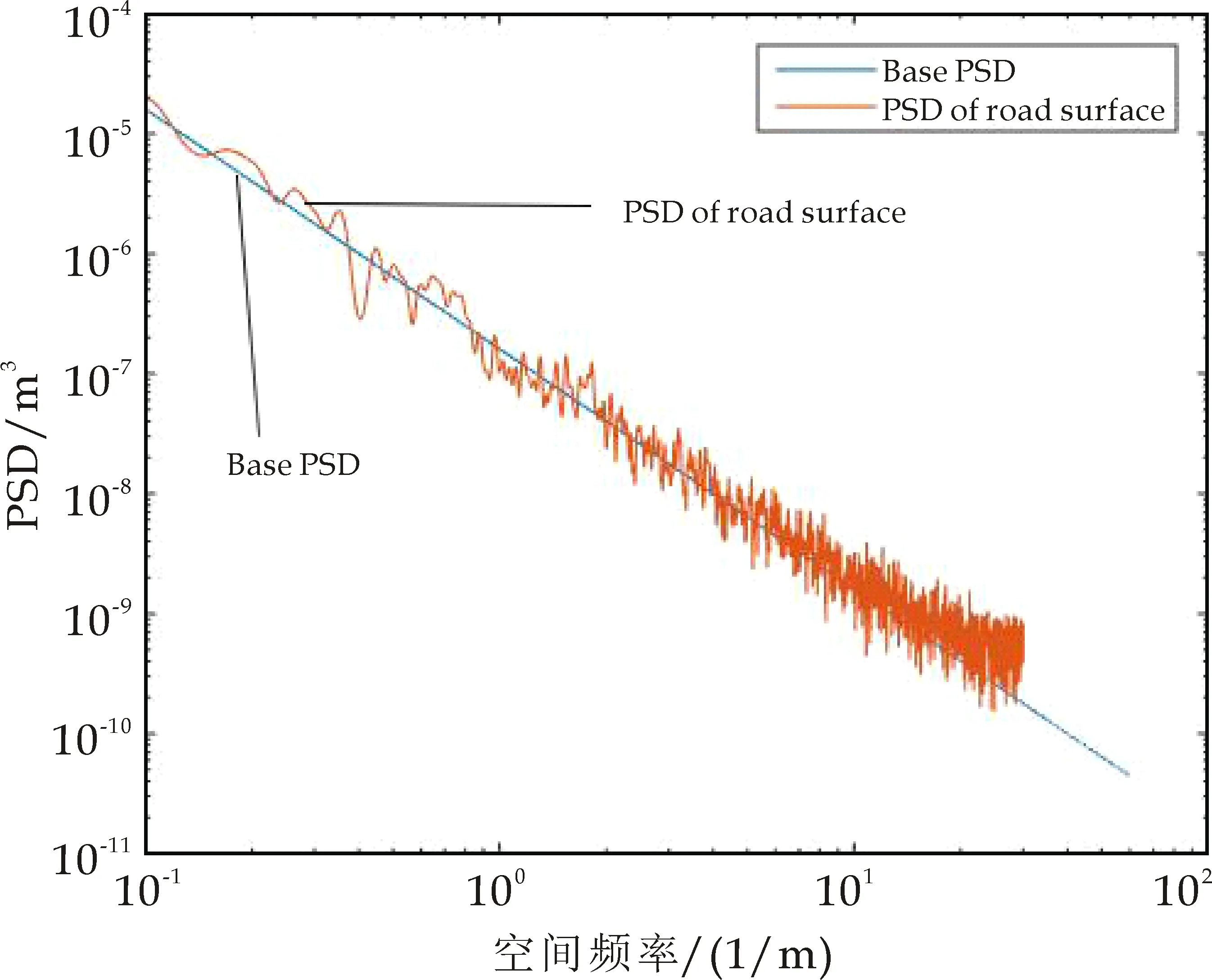
(b)标准路面和逆变换的空间频率功率谱图6 D级路面20 km/h基频同路面激励的关系

4 重卡与路面不平度的MATLAB振动响应

通过在D等级路面的仿真中，得知相应的路面不平度可看作该四轴重卡半挂车列车的运输状态等效为D级路面以20 km/h匀速行驶.利用MATLAB中ode15s对运动学方程进行求解二次微分方程，并带入重卡的相应部位方程，得到其相关振动的相对动载，最终得到驾驶室的相对动载.“相对动载”是机械系统动力学常用的振动响应指标，因为在许多复杂机构的多点力作用的机构物体，无法用普通的静定问题进行求解(文中的牵引车—鞍座—半挂车系统中对于半挂车就属于超静定问题)；在振动力学中需要假设相对静止的条件下进行求解，动载荷是指随时间作明显变化的载荷.“相对动载”是指该四轴重卡半挂车列车在以一定速度在相应等级路面运行过程中的随时间发生的动态载荷，目的是得出驾驶室的相对激励，通过激励进行位移和受力的分析.牵引车的前后悬置的相对动载表达式如式(15)、(16)所示：

Dqj1=kqj1[xj-d1xjy-xh+(l1+d1)xhy]+

(15)

Dhj1=khj1[xj+d2xjy-xh+(l1-d2)xhy]+

(16)

式(15)、(16)中：Gqj1—牵引车架前悬置静载，N；Ghj1—牵引车架后悬置静载，N.

某重卡的参数资料，得到1/2整车的牵引车架悬置位置响应如图7所示.通过图7可知某四轴重卡半挂车列车在D级路面以20 km/h匀速运行的10 s过程中，其牵引车架前悬置相对动载范围为-0.32～0.45,在0.3 s和9.7 s左右达到峰值.其动挠度范围约为-0.019～0.015 m,其趋势大体分布为先下降再逐渐上升,中间在3.3 s和5.6 s左右波峰.其牵引车后轴轮胎的相对动载范围为-0.45～0.33，在0.3 s和1.5 s左右达到峰值.其动挠度范围约为-0.018～0.014 m,其趋势大体分布为先上升后下降再逐渐上升，在3.2 s和5.8 s左右出现小的波峰.通过实验微型路面实测结果相符合.

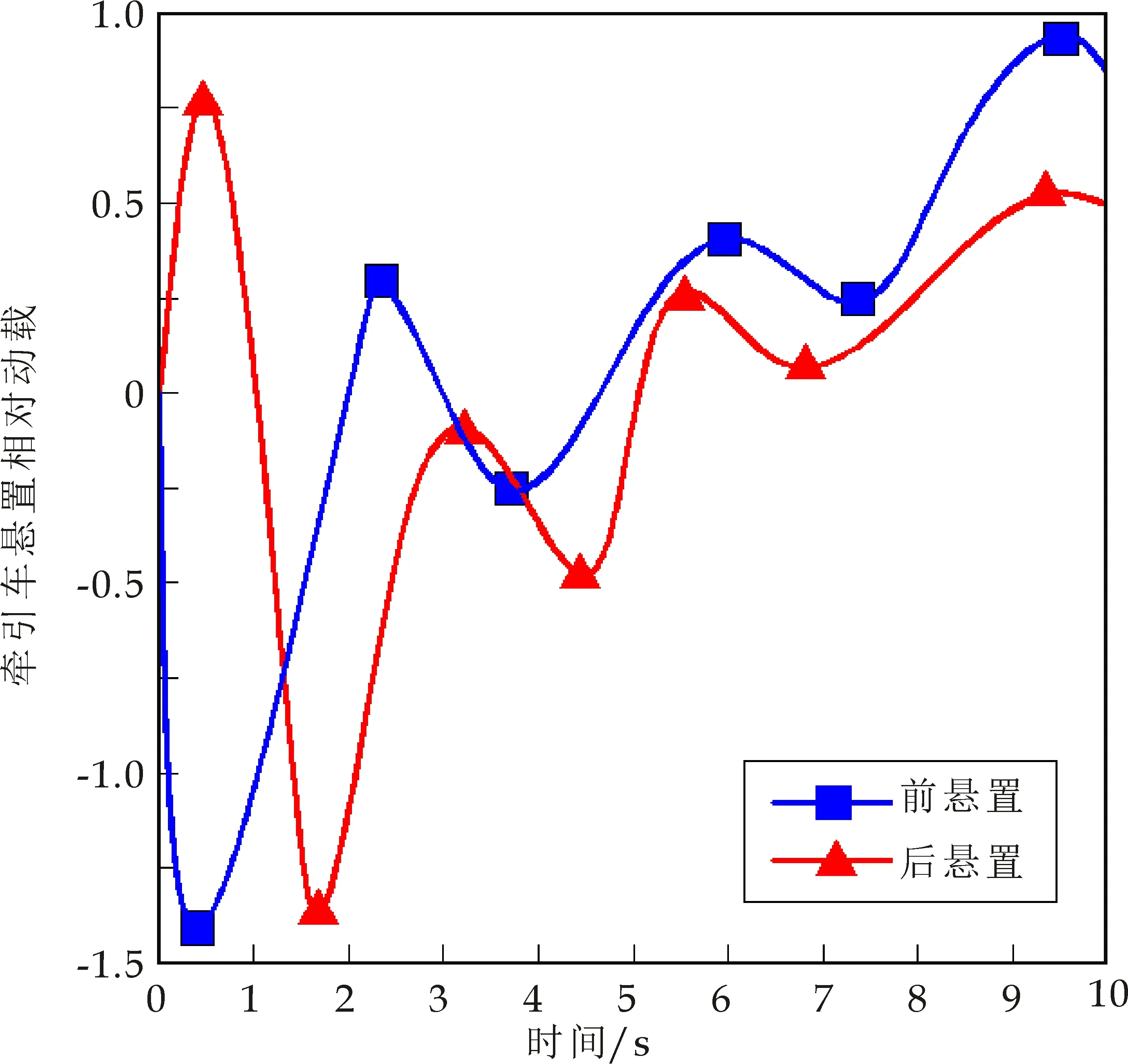
图7 1/2整车的牵引车架前后悬置相对动载

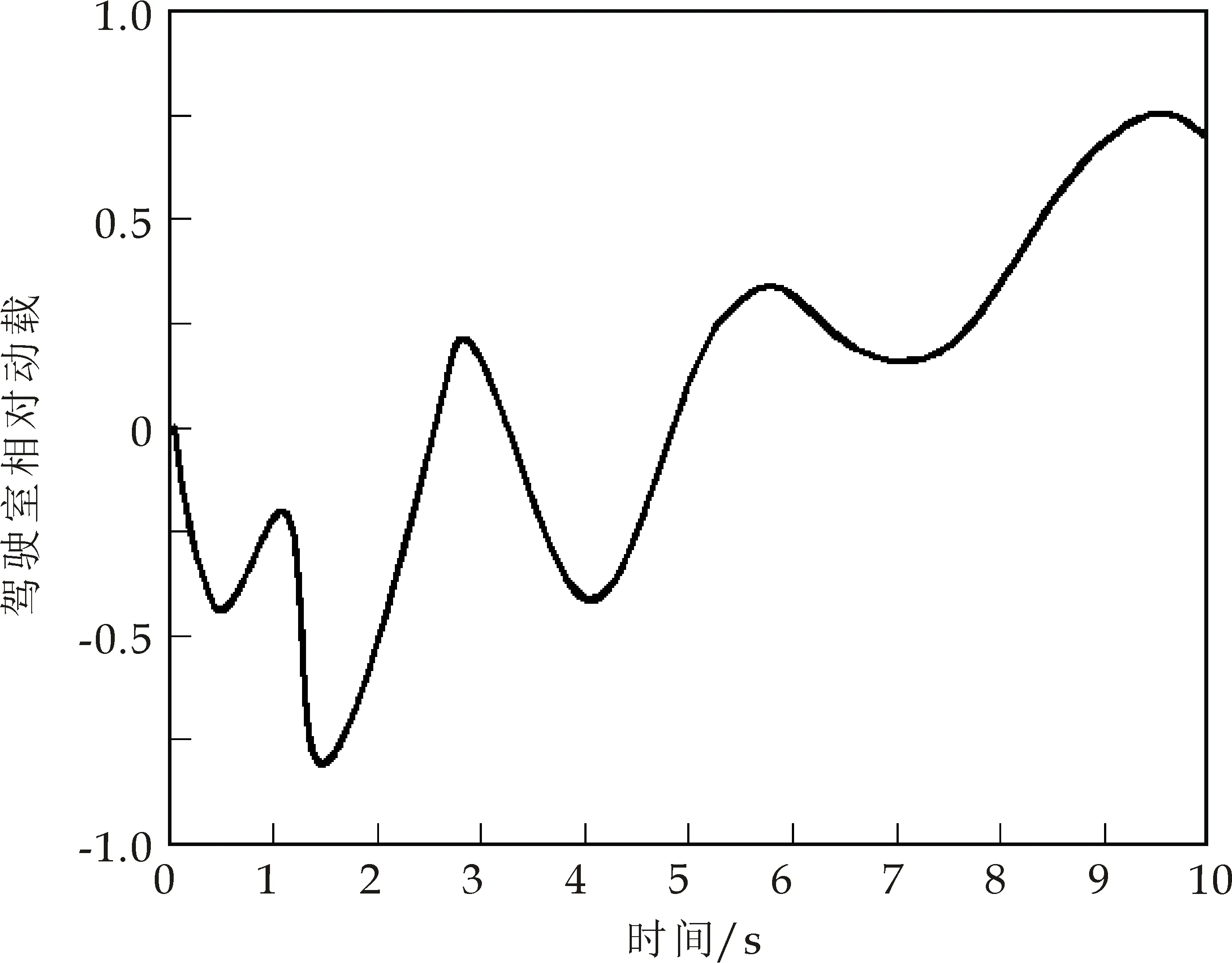
图8 驾驶室相对动载振动响应

5 结论

通过均值拟合得到图8，可知该四轴重卡半挂系统中在某D级路面以20 km/h行驶的过程呈现先下降后渐升趋势，与车轴实际所受激励基本一致，说明仿真结果可靠，通过驾驶室的相对动载可知该系统在1.5 s～2.5 s间会出现较大的振动响应.在微幅振动假设情况下将空间系统简化为平面系统，通过MATLAB的ode15s模块针对整车系统进行微分方程求解后得到具体1/2车体驾驶室相对动载的振动响应，得到系统的计算机仿真结果与实测相同路面等级车速对比结果可靠.这为后续利用该种方法在考虑鞍座情况下的多轴重卡开发及车路耦合领域的动力学仿真提供了新思路.

[1] 樊兴华,黄席樾,刘光波.九自由度汽车舒适性仿真[J].重庆大学学报(自然科学版),2000,23(4):127-132.

[2] 汪景倩.重型汽车随机振动仿真研究[D].锦州：辽宁工业大学,2013.

[3] 汪 斌.道路模拟试验台路面不平度再现方法研究[D].武汉：武汉理工大学,2010.

[4] 过学迅,徐 占,李孟良,等.路面不平度测量技术研究综述[J].中外公路,2009,29(5):47-51.

[5] 段虎明,石 峰,谢 飞,等.路面不平度研究综述[J].振动与冲击,2009,28(9):95-101，216.

[6] 单丽岩,侯相深,马松林.行车舒适性路面不平度评价标准[J].哈尔滨工业大学学报,2008,40(6):935-938.

[7] Cole D.J,Cebon D.Validation of an articulated vehicle simulation[J].Vehicle System Dynamics,1992,21(1):197-223.

[8] Vaduri Sunder S.V..Development of a simulation for preliminary assessment of ride[D].Carolina:Clemson University,1994.

[9] P.Velmurugana,K.Sankaranarayanasamyb,L.A.Kumaraswamidhasc,et al.Ride comfort analysis of unsuspended cabin tractor semi-trailer[J].Int.J.Vehicle Structures & Systems,2014,6(4)104-109.

[10] 李 杰,秦玉英,赵 旗.汽车随机振动的建模与仿真[J].吉林大学学报(工学版)，2010，40(2)：316-319.

[11] 殷 珺,陈辛波,吴利鑫,等.滤波白噪声路面时域模拟方法与悬架性能仿真[J].同济大学学报(自然科学版),2017,45(3):398-407.

[12] 张功学,叶 东.悬架参数对车辆平顺性的影响研究[J].

陕西科技大学学报(自然科学版),2016,34(5):147-151.

[13] 张功学,叶 东.满载汽车动力学模型及仿真[J].华侨大学学报(自然科学版),2017,38(1):1-6.

[14] 穆桂脂.基于AR模型及MLR模型的汽车行驶姿态预测[J].山东农业大学学报(自然科学版),2014,45(2):204-209.

[15] 刘云飞,杨柱元,雷 靖.基于小波包分析的线性回归拟合[J].云南民族大学学报(自然科学版),2012,21(2):109-111.