结合近邻传播聚类的选择性集成分类方法
2018-05-28姜丁菱何馨宇李丽双
孟 军 张 晶 姜丁菱 何馨宇 李丽双
(大连理工大学计算机科学与技术学院 辽宁大连 116023) (mengjun@dlut.edu.cn)
高通量测序技术的发展,为研究者提供了海量的基因表达数据,从中提取出有价值的信息已经成为生物信息学的研究热点[1-2].
植物在生长过程中经常会受到病虫害和环境因素的影响,如何预测并做好防治工作,对林业、农牧业、环境保护等多方面的发展将起到非常重要的作用.由于基因表达数据具有“高维度”、“小样本”和“高冗余”的特点,采用传统的单分类算法会出现分类稳定性差和准确率偏低等问题,因而对此类数据的分析需要处理能力较强的分类模型.
利用基分类器之间的信息互补性构建的集成分类模型,能够充分发挥各基分类器的优势,因此,具有更稳定、更精确的分类性能[3-4].
以往的集成模型通常只是以基因表达数据这一单一数据源为基础而设计的,由于基因之间具有生物学上的相互作用,融合已有的生物知识到分类模型中能够提高其分类性能.基因本体(GO)知识首先被应用到癌症的预测中,相关的实验表明结合生物知识能够提高预测结果的准确性并且增强其生物学角度上的可解释性与可信性[5].之后,结合通路(pathway)知识的预测模型同样被应用到了癌症的预测中[6].近年来,在疾病分类领域出现了结合超盒原理的pathway水平下的分类模型[7].
本文利用pathway知识对基因进行初步选择,使得筛选出的每个基因子集中只包含一个pathway知识单元中的基因.因为基因微阵列数据的高冗余性,只有极少数的基因与分类相关[8],所以在每个基因子集上采用了基于相交邻域粗糙集的基因选择模型为之后的分类工作选择出重要的、无冗余的基因.
在基分类器数量较多的情况下,会存在一些冗余的分类器,导致整体的差异性较差.为了提高集成分类的性能,对基分类器进行选择是十分必要的.选择性集成方法可以大致分为4类:迭代优化法、排名法、聚类法和模式挖掘法.在基于聚类技术的选择性集成中,Lin等人[9]提出了基于K-means聚类和循环序列的动态基分类器选择策略.Zhang等人[10]提出了基于谱聚类的集成剪枝方法.Krawczyk[11]在加权的Bagging集成分类中使用了基于聚类的剪枝方法.
本文采用基于近邻传播(affinity propagation, AP)聚类的选择性集成方法,在聚类的过程中最大化簇内的相似性和簇间的差异性[12].然后从每个聚簇内挑选出有代表性的基分类器进行集成,由于产生的基分类器聚簇之间具有较大的差异性,使得所选择的基分类器之间同样具有较大差异性.
本文的主要贡献有2个方面:
1) 在分类模型中引入先验知识,将pathway知识应用到对基因的选择中,利于基于相交邻域粗糙集的基因选择模型在不改变分类性能的前提下筛选出重要的基因.
2) 将聚类方法应用到集成分类模型中,采用基于AP聚类的选择性集成分类方法.
1 基于相交邻域粗糙集的基因选择
1.1 结合pathway的基因初选
KEGG的pathway数据库整合了分子互动网络的知识,包括图解的细胞生化过程,如代谢、细胞周期、信号传递、膜转运等,还包括同系保守的子通路等信息[13].该数据库包含7个方面的分子间相互作用和反应网络:
1) 新陈代谢;
2) 遗传信息加工;
3) 环境信息加工;
4) 细胞过程;
5) 生物体系统;
6) 人类疾病;
7) 药物开发[13].
每个pathway单元列出一个通路中所包含的所有基因.采用将每个知识单元中所包含的基因与基因微阵列数据中的基因相对应的方式来进行2种数据的结合.每个pathway单元对应一个基因子集,同时形成一个只包含该基因子集中基因的训练集.由于各基因子集中包含不同的基因,数据分布差异显著,因此基于这些基因子集训练得到的基分类器之间将具有显著的差异性.并且这种知识融合方法还能够降低数据的维数,因此适合于对基因微阵列数据进行处理.目前还有一些基因在相关的pathway数据库中没有完善的注释信息.随着生物知识的完善,结合pathway的分类方法将会有更好的效果.

对于GEDT=(U,C∪D,V,f),将其与pathway知识结合,可以得到一种如表1所示的结合pathway知识的信息表,其中si(i=1,2,…,n)表示基因表达数据中的第i个样本,fkji表示样本si在pathway知识单元Pk(k=0,1,…,m)中基因pkj(j=1,2,…,|Pk|)上的表达量.

Table 1 Information Table Formed by Combing Microarray Data with Pathway Knowledge
1.2 基因选择算法
Yao和Lin[15]对Pawlak提出的经典粗糙集模型进行了一定的扩展,将原有的等价关系用任意的二元关系替代,提出了广义的粗糙集理论,该理论适用于数值型数据的处理.广义的粗糙集将原理论中的基本集合由等价类变成了现有理论中的邻域,因此新提出的模型也可以看作是基于邻域的粗糙集模型.本文使用基于相交邻域的粗糙集模型对基因进行选择.相交邻域较之于邻域,能够更大程度上减少属性之间的相互影响[16].对于基因选择问题,在构建邻域时仅从表达数据本身来说,无法准确获知基因之间的关联性.因此,相交邻域的定义形式更具合理性.
定义2[15].R是U上的一个二元关系,给定对象x∈U,x的邻域表示为
NR(x)={y|xRy,y∈U}.
(1)
定义3[16]. 对于属性集合B⊆C,给定对象x∈U,x的相交邻域定义为
INB(x)={y|∀b∈B,|fb(x)-fb(y)|≤δb,y∈U}.
(2)
定义4[15]. 对于对象集合X⊆U,给定属性集合B⊆C,则基于相交邻域,集合X的上、下近似集分别定义为

(3)

(4)
粗糙集理论的基本思想是利用上近似集和下近似集所确切表示的对象集合来近似表示U上的一个模糊的对象集X.
定义5[15]. 对于对象集合X⊆U,基于属性子集B⊆C,X的正域、负域和边界的定义形式分别为
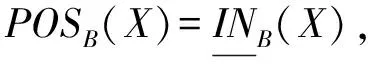
(5)
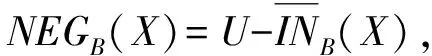
(6)
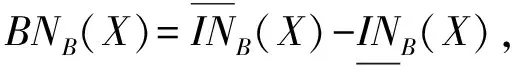
(7)
其中,正域是确定属于集合X的所有对象组成的集合,其对象范围与下近似集相同;负域是确定不属于集合X的所有对象的集合,即属于论域U却不属于上近似集的对象所组成的集合;边界集合是属于上近似集而不属于下近似集的对象所组成的集合,即无法确定是否能归类于集合X的对象集合.
决策表上的属性约简是指对条件属性进行的约简,条件属性的约简与决策属性是相对的.
定义6[17]. 决策表GEDT=(U,C∪D,V,f),对于属性集合B⊆C,相对于决策属性集D的正域定义为
(8)
其中,UIND(D)是由等价关系IND(D)导出的所有不同等价类的集合,每个等价类中的样本具有相同的类别标签.
定义7[17]. 对于条件属性c∈B⊆C,如果POSB-{c}(D)=POSB(D)成立,则称属性c在条件B中相对于决策属性D是非必要的,则属性c是可以约简的;如果条件不成立,称属性c在条件属性B中相对于决策属性D是必要的,则是不可约简的.
定义8[17]. 对于条件属性集合B⊆C,如果B中的每一个属性相对于决策属性D都是必要的,则称条件属性子集B相对于决策属性D是独立的.
定义9[17]. 对于条件属性集合B⊆C,集合E⊆B,当且仅当E相对于决策属性D是独立的,且满足公式POSE(D)=POSB(D),则E被称为B的一个相对于决策属性D的约简.
约简中的每一个条件属性相对于决策属性都是必要的,并且约简出的条件属性子集与原始条件属性集合具有同等的分类性能.将以上的属性约简流程列于算法1中.
算法1. 基于相交邻域的属性约简算法.
输入:决策表GEDT={U,C∪D,V,f}、待约简的属性子集B、相交邻域阈值δ;
输出:B的相对于决策属性D的约简RED.
① 对于每个对象x∈U,计算其基于属性子集B的相交邻域INB(x).
② 将所有对象依据类别属性D={d}进行划分,得到基于决策属性的等价类集合UIND(D).
③ 计算在属性集合B条件下相对于决策属性D的正域POSB(D).
④ 令RED=B.
⑤ 对于每个对象x∈U,计算其基于属性子集RED-{b}的相交邻域INRED-{b}(x),并且计算在属性子集RED-{b}条件下的相对于决策属性D的正域POSRED-{b}(D).
如果POSRED-{b}(D)=POSB(D),则RED=RED-{b}.
⑥ 采用秩和检测对基因进行排序,从后向前依次进行验证.重复步骤⑤直到所有的基因b∈B都进行了验证.
2 结合近邻传播聚类的选择性集成
在构建集成分类模型的过程中,会产生多个基分类器,对基分类器进行剪枝能够减少所需的存储空间和计算资源[18-19].另外,Zhou等人[20-21]通过实验表明选择部分合适的基分类器进行集成,其分类效果优于对全部基分类器进行集成,这也是选择性集成的另外一个优势.
本文使用基于AP聚类的选择性集成分类方法,首先将基分类器划分成多个聚簇,然后从每个聚簇中选择作为聚簇中心的基分类器进行集成.
2.1 近邻传播聚类算法
由Frey和Dueck[22]提出的AP聚类算法,由于其较好的性能已被成功应用于数据挖掘的许多领域[23].在AP聚类算法中,每一个数据点都被视为潜在的聚簇中心,数据点之间不断地进行信息传递直到算法收敛或迭代结束.与传统的聚类方法如K-means和自组织映射相比,AP聚类算法有3个优势:
1) 不需要事先指定聚簇个数,也不需要初始化聚簇中心点;
2) 聚类结果更加稳定与准确;
3) 在达到同样聚类精确度的条件下所需时间更短.
AP聚类算法以相似性矩阵S作为输入,矩阵中元素s(i,j)表示数据点i和j之间的相似性,数值越大则表明2个数据点之间的相似性越大.矩阵对角线上的值s(k,k)称作数据点k的参考度(pre-ference),该值越大说明该数据点更加适合作为聚簇中心,因此生成的聚簇个数也就越多.一般而言,将所有数据点的preference值设置为相同的数值,以保证所有的数据点具有同等的机会成为聚簇中心.
AP聚类算法在迭代的过程中传递2种信息,Responsibility和Availability.r(i,k)代表前者,表示数据点k作为数据点i的聚簇中心的适应程度;a(i,k)代表后者,表示数据点i选择数据点k作为其聚簇中心的倾向程度.
r(i,k)=s(i,k)-max(a(i,j)+s(i,j)),
(9)
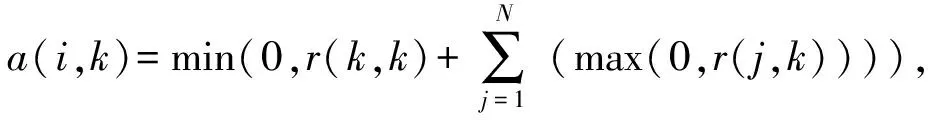
(10)
其中,j∈{1,2,…,N},j≠k.
AP聚类可以自动确定聚簇个数,在迭代的过程中如果r(k,k)+a(k,k)>0,就选择数据点k作为聚簇中心.迭代结束之后将剩余的数据点分配给距其最近的聚簇中心.
为了提高AP聚类算法的稳定性,引入阻尼系数λ,这样一来,r(i,k)和a(i,k)就受到上一次迭代计算值的约束.改进后的计算为
ri=(1-λ)ri+λri-1,
(11)
ai=(1-λ)ai+λai-1,
(12)
其中,ri和ai代表第i次迭代的结果,ri-1和ai-1代表第i-1次的迭代结果.
本文使用AP聚类算法对基分类器依据其在剪枝集上的分类结果进行聚类,并且选择作为聚簇中心的基分类器进行集成,以保证被选择的基分类器之间具有较大的差异性.
2.2 相似性矩阵计算
在对基分类器进行聚类时,依据各基分类器在剪枝集上的分类结果计算相似性,并采用基于kappa系数和准确率的相似性计算公式.
Cohen[24]提出的kappa系数是对一致性的一种度量,这种评价系数能够消除因随机性带来的误差,本文采用kappa系数来测量基分类器之间的相似性[25].
定义10[24]. 依据基分类器的分类结果,kappa系数的计算为

(13)
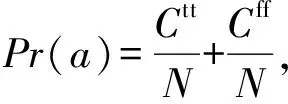
(14)

(15)

kappa系数的数值范围是-1~1.当kappa<0时,表明一致性比由随机性引起的还差;当kappa>0时,数值越大表明一致性越好.
定义11. 基分类器之间基于kappa系数的相似性定义为
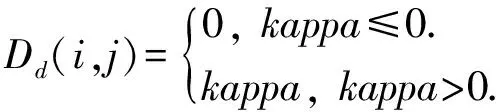
(16)
在对基分类器进行聚类时,除了选择出具有差异性的基分类器集合之外,各个基分类器的分类准确率也是影响集成结果的十分重要的因素.kappa系数只是对基分类器之间分类结果的相似性进行了度量,而在2个基分类器同时分类错误的情况下,其结果同样是相似的,所以没有考虑到其分类性能.因此本文定义了基于kappa系数和分类准确率的相似性计算公式.
在剪枝集中有N个样本的情况下,当且仅当Hi和Hj对第k个样本同时分类正确时,ck=1,其他情况下ck=0.
定义12. 基分类器之间基于准确率的相似性定义为
(17)
定义13. 基分类器之间基于kappa系数和分类准确率的相似性计算为
s(i,j)=αDd(i,j)+(1-α)Da(i,j),
(18)
其中,α∈[0,1],是基于kappa系数的相似性的权重.
2.3 选择性集成分类流程
在结合近邻传播聚类的选择性集成分类模型(selective ensemble classification integrated with affinity propagation clustering,SECIAPC)中,将pathway作为先验知识引入到基因微阵列数据的分类中,之后使用基于相交邻域粗糙集的基因选择模型对每个基因子集进行属性约简.在基分类器选择阶段,采用基于AP聚类的选择性集成方法,集成分类模型流程如图1所示.
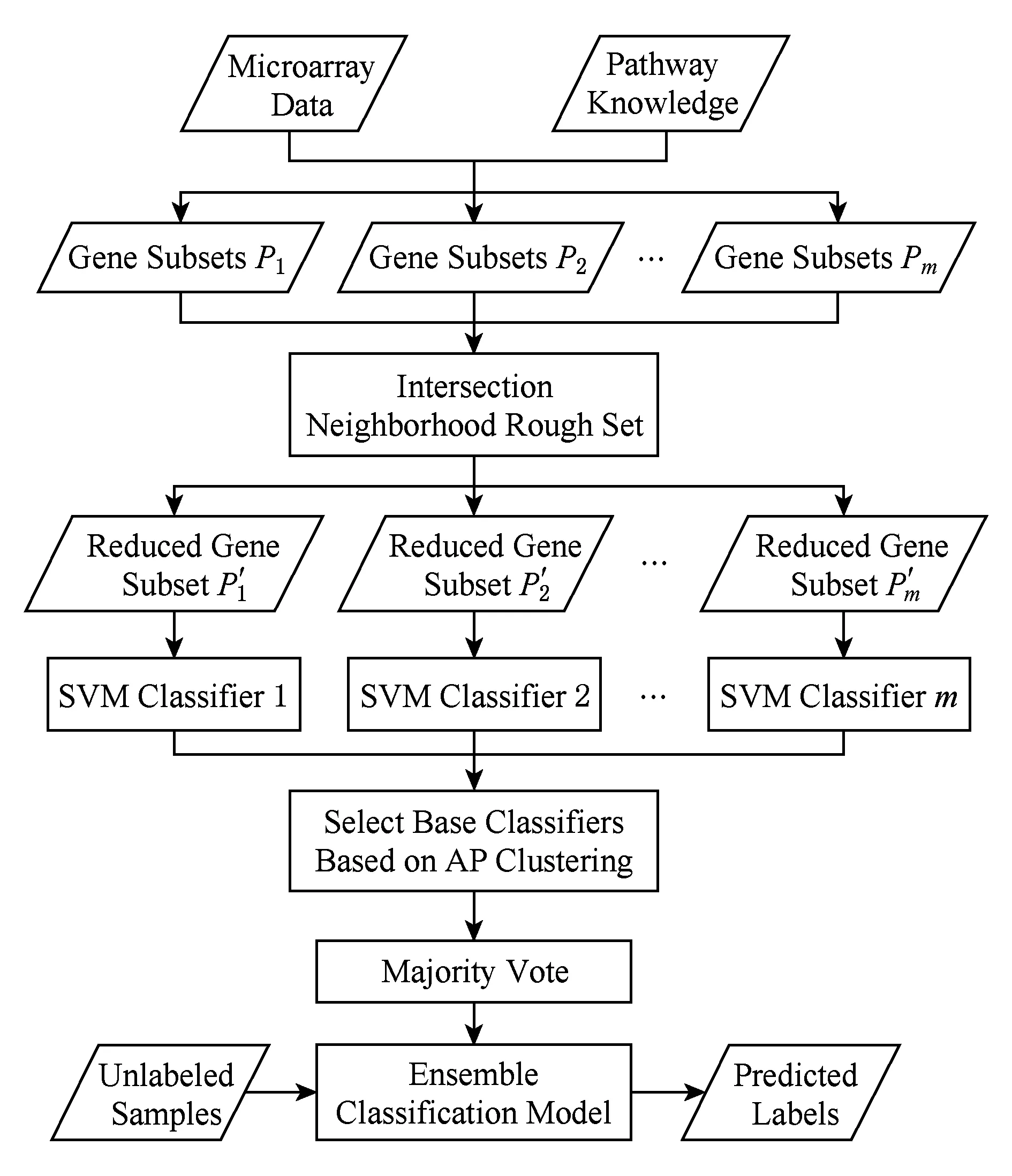
Fig. 1 Flow chart of classification model图1 分类模型流程
步骤1. 基因微阵列数据与pathway知识相结合生成多个基因子集.
步骤2. 采用基于相交邻域粗糙集的基因选择模型在每个基因子集中筛选出重要的基因.
步骤3. 在每个约简之后的基因子集上训练SVM基分类器.
步骤4. 全体基分类器对剪枝集进行分类,依据分类结果采用AP聚类算法对分类器进行聚类,并选择作为聚簇中心的基分类器进行集成.
步骤5. 步骤4选择出的基分类器对测试集进行分类,使用简单多数投票法对分类结果进行融合.
3 实验结果与分析
3.1 数据集
由于拟南芥的生物学实验数据和基因注释信息相对比较丰富,所以常被用在不同类型的植物胁迫响应的研究中[26].本文采用拟南芥胁迫响应数据集和相关的pathway知识来对分类模型进行评估,从公开的生物信息网站GEO*http://www.ncbi.nlm.nih.gov/geo/下载了Arabidopsis-Drought,Arabidopsis-Oxygen和Arabidopsis-TEV三个数据集,它们分别对应于拟南芥干旱胁迫、氧气胁迫和烟草蚀纹病毒胁迫.具体信息如表2所示,每个数据集都包含实验组和对照组,分别记为Class1和Class2.本文从数据库*https://www.arabidopsis.org下载了拟南芥相关的pathway数据,其中包含121个pathway知识单元,对应形成121个基因子集,并且每个基因子集对应生成1个基分类器.
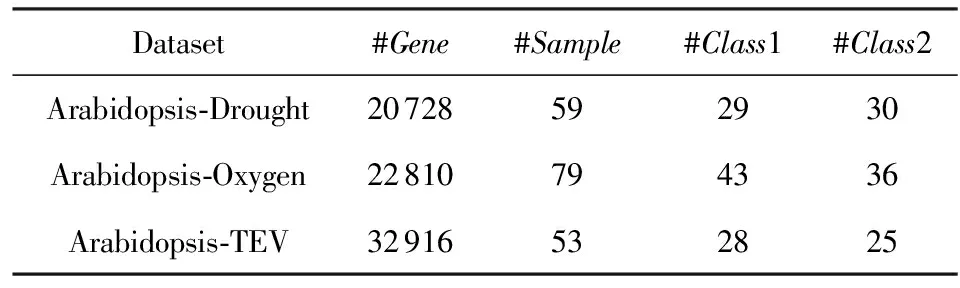
Table 2 Detail Information of Datasets表2 数据集的具体信息
3.2 数据预处理及参数设置
为避免因基因表达数据数值范围不一致带来的分类误差,同时也便于邻域阈值的确定,所有数据被标准化到[-1,1].实验中设定相交邻域阈值δ的变化范围为0.05~0.95,步长为0.1,并且在每次实验中假设各个基因对应的阈值相同.AP聚类中的阻尼系数λ=0.1,基分类器的距离计算公式中权值α设置为从0.1到0.9,步长为0.1.随机选择60%的样本作为训练样本,20%的样本作为剪枝样本,余下的作为测试样本.实验中采用支持向量机(support vector machine, SVM)作为分类算法生成基分类器,设定SVM分类器的核函数为具有较好分类性能和良好适应能力的RBF核函数K(x,y)=exp(-γ‖x-y‖2).
二分类问题的评价标准基于4种基础的指标:真阳性(true positives,TP)、假阳性(false positives,FP)、真阴性(true negatives,TN)和假阴性(false negatives,FN).
对分类模型选用准确率(accuracy,ACC)、敏感性(sensitivity,SN)、特异性(specificity,SP)和几何平均数(geometric mean,G-mean)四种标准评价其性能.准确率反映了对所有样本的分类准确率;敏感性和特异性分别反映对正、负类样本的分类准确率;几何平均数从全局衡量了对正、负类样本的分类性能.4种评价标准的定义为
ACC=(TP+TN)(TP+TN+FP+FN),
(19)
SN=TP(TP+FN),
(20)
SP=TN(TN+FP),
(21)

(22)
3.3 结果分析
在本文使用的3个数据集上,通过实验表明当δ分别取值为0.45,0.55,0.65时、α分别取值为0.1,0.2,0.8,0.9时得到较好的分类结果,但是不同数据集上δ和α对分类结果的影响不同,所以在不同数据集上选取分类性能最好的δ和α值.为了更好地验证本文提出方法的优势,将该方法与单个的SVM分类器和Random Subspace,Bagging,AdaboostM1和Stacking这4种常用的集成分类方法进行比较.利用Weka软件对这4种方法的实现进行对比实验[27].Random Subspace的基本原理是抽取不同的属性子集,对应每个属性子集形成一个训练集;Bagging的原理是不断的有放回的抽取样本子集;AdaboostM1方法在对样本进行抽样的过程中,对被错误分类的样本赋予更大的权重,来提升对这些样本的分类能力;Stacking方法一般采用2层结构,将第1层的分类结果作为下一层的输入.本文提出的SECIAPC方法采用结合pathway知识的方式生成不同的基因子集,与以上4种集成方法不同的是使用AP聚类对基分类器进行选择,并对选择出的部分基分类器进行集成.所有的集成分类方法都采用SVM分类器进行集成,3个数据集上分类性能的比较如表3~5所示.
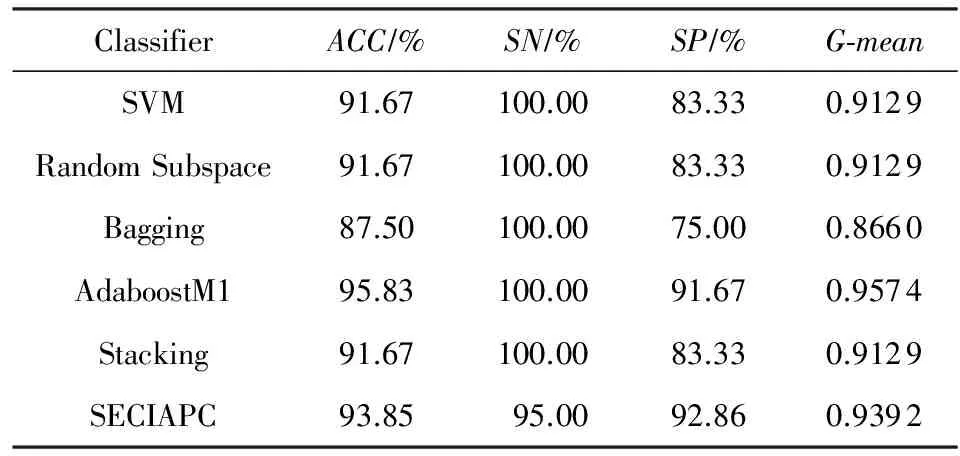
Table 3 Classification Results on Arabidopsis-Drought Dataset
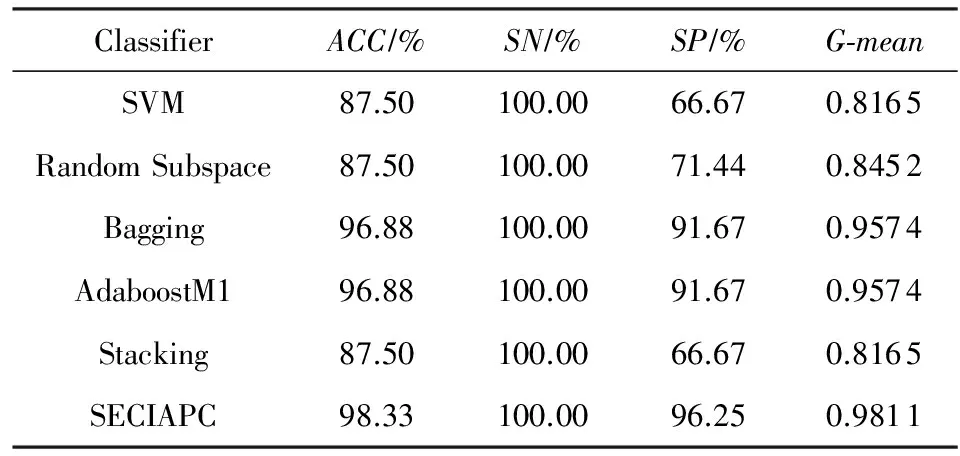
Table 4 Classification Results on Arabidopsis-Oxygen Dataset

Table 5 Classification Results on Arabidopsis-TEV Dataset表5 Arabidopsis-TEV数据集上的分类结果
在Arabidopsis-Drought数据集上,SECIAPC方法的准确率和几何平均数与其他方法中性能最好的AdaboostM1相当,对负类样本的分类准确率有所提高.与其他3种集成方法相比,SECIAPC方法的性能大幅度提高,特别是在对负类的分类性能上提高了至少10%.在Arabidopsis-Oxygen数据集上,在准确率和几何平均数方面,SECIAPC与AdaboostM1和Bagging这2种性能最好的方法相比提高了近2%.在Arabidopsis-TEV数据集上,其他方法对于正负类样本的分类能力极其不均衡.SECIAPC方法在准确率上与其他方法比较至少提高了12%,并且极大地提高了对负类样本的分类性能.
为了验证所选基因的生物学意义,使用GO术语*http://www.geneontology.org/检查部分被选择基因的功能注释,GO数据库中运用Term的概念来显示基因特性,这些GO Term被划分为3类:细胞成分(cellular component, CC)、分子功能(molecular function, MF)和生物过程(biological process, BP),分别对应表中的3种类别.部分被选择的基因的详细注释如表6所示.可以看出,这些基因都与胁迫响应相关.
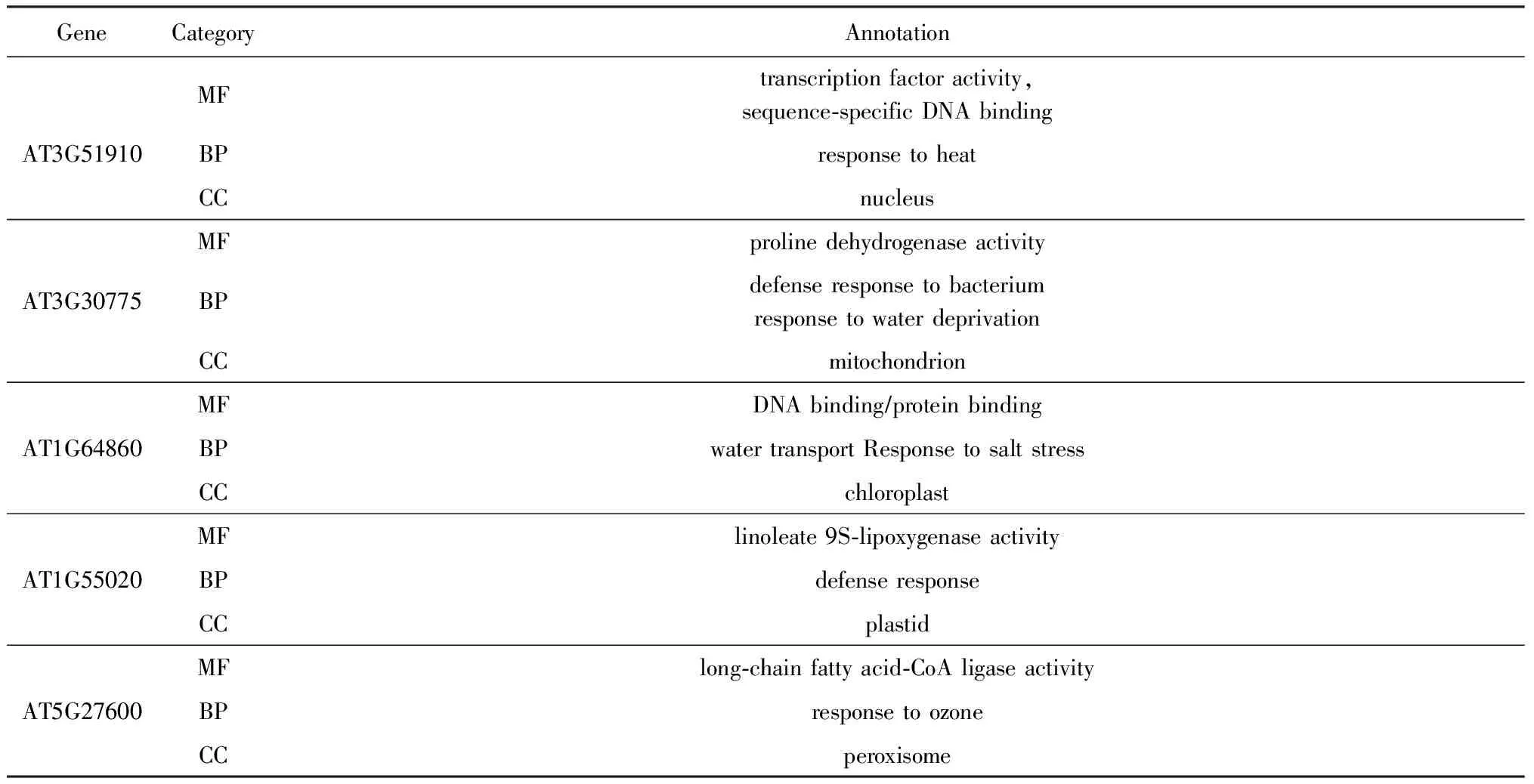
Table 6 Gene Annotations in GO for Some Selected Genes表6 部分所选基因的GO基因注释信息
4 结束语
本文采用基于相交邻域粗糙集的基因约简模型作用在由pathway产生的信息表上,在引入先验知识的同时进行重要基因的选择.使用基于AP聚类的选择性集成方法,在基分类器选择的过程中将分类和聚类2种机器学习技术进行结合,进一步提高了集成分类的性能.
在3个拟南芥胁迫响应相关数据集上的实验结果表明,提出的SECIAPC方法能够得出较好的分类结果.同时与单分类器、传统集成方法的分类结果进行对比,其分类性能有很大的提升.由于基因微阵列数据的高维属性,整个集成分类模型的分类效率有待进一步提高.
[1]Maji P, Garai P. On fuzzy-rough attribute selection: Criteria of max-dependency, max-relevance, min-redundancy, and max-significance[J]. Applied Soft Computing, 2013, 13(9): 3968-3980
[2]Maji P, Paul S. Rough-fuzzy clustering for grouping functionally similar genes from microarray data[J]. IEEE/ACM Trans on Computational Biology and Bioinformatics, 2013, 10(2): 286-299
[3]Landesfeind M, Kaever A, Feussner K, et al. Integrative study of arabidopsis thaliana metabolomic and transcriptomic data with the interactive marvis-graph software[J]. PeerJ, 2014, 2: Article No.e239
[4]Rokach L. Ensemble-based classifiers[J]. Artificial Intelligence Review, 2010, 33(1/2): 1-39
[5]Chen Xi, Wang Lily. Integrating biological knowledge with gene expression profiles for survival prediction of cancer[J]. Journal of Computational Biology, 2009, 16(2): 265-278
[6]Bandyopadhyay N, Kahveci T, Goodison S, et al. Pathway-Based Feature Selection Algorithm for Cancer Microarray Data[J]. Advances in Bioinformatics, 2010, 2009(5235): 103-118.
[7]Gatza M L, Lucas J E, Barry W T, et al. A pathway-based classification of human breast cancer[J]. Proc of the National Academy of Sciences, 2010, 107(15): 6994-6999
[8]Zhang Lijuan, Li Zhoujun. Gene selection for cancer classification in microarray data[J]. Journal of Computer Research and Development, 2009, 46(5): 794-802 (in Chinese)
(张丽娟, 李舟军. 微阵列数据癌症分类问题中的基因选择[J]. 计算机研究与发展, 2009, 46(5): 794-802)
[9]Lin Chen, Chen Wenqiang, Qiu Cheng, et al. LibD3C: Ensemble classifiers with a clustering and dynamic selection strategy[J]. Neurocomputing, 2014, 123: 424-435
[10]Zhang Huaxiang, Cao Linlin. A spectral clustering based ensemble pruning approach[J]. Neurocomputing, 2014, 139: 289-297
[11]Krawczyk B. Forming ensembles of soft one-class classifiers with weighted bagging[J]. New Generation Computing, 2015, 33(4): 449-466
[12]Ding Xiangwu, Guo Tao, Wang Mei, et al. A clustering algorithm for large-scale categorical data and its parallel implementation[J]. Journal of Computer Research and Development, 2016, 53(5): 1063-1071 (in Chinese)
(丁祥武, 郭涛, 王梅, 等. 一种大规模分类数据聚类算法及其并行实现[J]. 计算机研究与发展, 2016, 53(5): 1063-1071)
[13]Kanehisa M, Goto S, Hattori M, et al. From genomics to chemical genomics: New developments in KEGG[J]. Nucleic Acids Research, 2006, 34(Suppl 1): D354-D357
[14]Pawlak Z. Rough sets[J]. International Journal of Computer & Information Sciences, 1982, 11(5): 341-356
[15]Yao Yiyu, Lin Tsauyoung. Generalization of rough sets using modal logic[J]. Intelligent Automation and Soft Computing, 1996, 2(2): 103-120
[16]Meng Jun, Zhang Jing, Li Rui, et al. Gene selection using rough set based on neighborhood for the analysis of plant stress response[J]. Applied Soft Computing, 2014, 25: 51-63
[17]Pawlak Z. Imprecise categories, approximations and rough sets[G] //Rough Sets. Beijing: Springer, 1991: 9-32
[18]Ni Zhiwei, Zhang Chen, Ni Liping. Haze forecast method of selective ensemble based on glowworm swarm optimization algorithm[J]. Pattern Recognition and Artificial Intelligence, 2016, 29(2): 143-153 (in Chinese)
(倪志伟, 张琛, 倪丽萍. 基于萤火虫群优化算法的选择性集成雾霾天气预测方法[J]. 模式识别与人工智能, 2016, 29(2): 143-153 )
[19]Tang Chao, Wang Wenjian, Li Wei, et al. Human action recognition algorithm based on selective ensemble rotation forest[J]. Pattern Recognition and Artificial Intelligence, 2016, 29(4): 313-321 (in Chinese)
(唐超, 王文剑, 李伟, 等. 基于选择性集成旋转森林的人体行为识别算法[J]. 模式识别与人工智能, 2016, 29(4): 313-321)
[20]Zhou Zhihua, Wu Jianxin, Tang Wei. Ensembling neural networks: Many could be better than all[J]. Artificial Intelligence, 2002, 137(1): 239-263
[21]Zhou Zhihua, Tang Wei. Selective ensemble of decision trees [C] //Proc of the 9th Int Workshop on Rough Sets, Fuzzy Sets, Data Mining, and Granular-Soft Computing. Berlin: Springer, 2003: 476-483
[22]Frey B J, Dueck D. Clustering by passing messages between data points[J]. Science, 2007, 315(5814): 972-976
[23]Leone M, Weigt M. Clustering by soft-constraint affinity propagation: Applications to gene-expression data[J]. Bioinformatics, 2007, 23(20): 2708-2715
[24]Cohen J. A coefficient of agreement for nominal scales[J]. Educational and Psychological Measurement, 1960, 20(1): 37-46
[25]Ben-David A. Comparison of classification accuracy using Cohen’s weighted kappa[J]. Expert Systems with Applications, 2008, 34(2): 825-832
[26]Karim S. Exploring Plant Tolerance to Biotic and Abiotic Stresses[D]. Uppsala, Sweden: Swedish University of Agricultural Sciences, 2007
[27]Hall M, Frank E, Holmes G, et al. The WEKA data mining software: An update[J]. ACM SIGKDD Explorations Newsletter, 2009, 11(1): 10-18
