指定验证者与可撤销重加密的可搜索加密方案

徐 潜 谭成翔 樊志杰 冯 俊 朱文烨 校 娅

(同济大学电子与信息工程学院 上海 201804) (1062842783@qq.com)

电子健康记录系统(electronic health record, EHR)为用户提供了存储和管理个人健康记录的功能，辅助医生为病人制定合理的医疗方案[1].在EHR系统中，用户将自身的病例数据外包到服务器端，不同的医院和医生可以与用户一起分享健康数据，从而为用户提供更加准确和优质的服务.目前已经有许多较为成熟的EHR系统，例如微软公司推出的Microsoft Medical Vault以及谷歌的Google Health等.

由于外包到服务端的数据可能包含有用户的敏感隐私信息，而服务端的非完全可信状态可能导致隐私数据发生泄漏.因此，在数据外包前进行加密处理就成为防止其被非法访问的一种有效的途径.但是，其他合法的数据使用者也需要获得数据的访问权，例如EHR系统中的医院或者医生就需要在特定的环境下访问病人的病例数据从而做出正确的诊断.最直接的方法就是将用户的全部加密数据下载到本地，然后利用共享的密钥进行解密并执行数据的访问操作.然而由于数据量可能非常庞大，全部下载会给本地的计算资源带来难以承受的负荷[2].所以，依赖于用户提交的关键词并有选择地返回使用者所需要的数据，就成为一种有效可行的解决方法.但是，由于用户数据在服务器端是以密文的形式存储，传统的明文关键词搜索方案并不适用.因此，研究高效的可搜索加密方案就对密文环境下用户隐私数据的安全访问控制产生重要的意义.

可搜索加密方案(searchable encryption, SE)可以在保证数据隐私性和安全性的基础上提供密文检索等操作.目前已有许多可搜索加密策略，例如文献[3-5].Liu等人[4]利用从明文中提取出的关键词组成词典设计了密文检索策略；He等人[5]基于双线性对提出了一种较文献[4]更加高效的支持模糊关键字查询的方案.总体来说，目前已有的SE加密策略可以分成2类：1)对称的可搜索加密策略(sear-chable symmetric encryption, SSE)，这类策略要求在数据访问者之间共享密钥；2)非对称的可搜索加密策略(searchable asymmetric encryption, SAE)，也称为公钥可搜索加密策略(public key encryption scheme with keyword search, PEKS).在公钥可搜索加密研究领域，已有一些研究成果，如文献[6-8].其中，Zhang等人[8]提出了一种支持合取关键词搜索的PEKS方案；而Shen等人[9]则在PEKS策略的基础上提出了支持内积运算的谓词加密(predi-cate encryption, PE)方案.较之传统的PEKS方案，PE方案可以提供更加细粒度的密文访问控制.同时，谓词加密也可以引申出很多高效可行的加密策略，这其中就包括隐藏向量加密(hidden vector encryption, HVE)方案.与传统的PEKS加密方案一样，在HVE加密方案中，数据的发送者Bob与数据的接收者Alice是不同的实体.只有当数据使用者依据关键词生成的访问令牌(token)与数据拥有者定义的数据关联属性(attribute)匹配时，检索操作才可以顺利执行[10].较之一般的PEKS方案或者PE方案，HVE加密策略可以更加有效地支持关键词的合取和范围搜索等集合操作，因此可以被应用在诸如EHR系统等敏感数据检索领域.

目前已有许多关于HVE加密方案的研究成果，例如文献[11-13].其中，Mitsuhiro等人[13]设计的HVE加密策略引入了代理重加密的概念，但是代理者的访问权限无法变更；同时，文献[11-13]的方案均无法抵御离线关键词测试攻击(off-line keyword guessing attack, KG).在EHR系统中，检索关键词一般均取自范围较小的特定医学术语集合，这就给了攻击者实施离线关键词测试攻击的机会.同时，数据拥有者需要授权医生对其敏感的病例数据进行访问，而访问权限应该可以由患者进行细粒度的管控，当患者不希望医生再执行访问操作，或者当患者更改了医院或医生时，之前的访问权限能够被及时地撤销.一种可行的方法是当访问权限发生改变时，数据拥有者重新加密所有敏感数据，但这会带来很大的计算负荷.针对加密方案中数据访问权的细粒度可控问题，文献[14-17]均提出了相应的解决方案.其中Yang等人[14]提出了基于时间控制的代理重加密PEKS方案.通过引入可信的时间服务器生成时间戳，并将时间戳嵌入到搜索令牌中来实现代理访问权的控制.但是，文献[14]的验证操作需要O(l)次的双线性对运算(l为查询向量的维数)，重加密操作需要额外的O(l)次的指数运算，令牌的空间复杂度也是O(l)，因此方案在实际应用时效率较低.

综上所述，目前公钥可搜索加密或HVE加密的研究领域尚存在3点可以改进的地方：

1) 已有的HVE方案尚未考虑离线关键词测试攻击问题.

2) 已有的支持代理重加密的HVE方案不具有细粒度的代理权限管控的能力.

3) 已有的支持代理重加密的PEKS方案要么只能检索单个关键词，要么在令牌尺寸、解密和重加密的时间复杂度等方面线性依赖于查询向量的维数，导致方案的实际应用效率较低.

针对这些问题，本文基于HVE加密方案，提出了支持指定验证者与可撤销代理重加密的DT_aPRE_HVE加密策略.

本文的主要贡献归纳为4个方面：

1) 提出的DT_aPRE_HVE方案是第1个支持基于时间的可撤销代理重加密功能的HVE加密策略.与已有方案相比，本文将时间戳引入到重加密过程中，使数据拥有者可以为不同的数据访问者指定不同的时间区间，彼此互不影响，从而达到细粒度权限控制的目的.相比于文献[14]，本文方案不需要引入额外的时间服务器，降低了系统复杂度.同时，由于时间戳是嵌入到密文中的，即使数据拥有者处于离线状态，数据的访问权限也可以被自动管控.

2) 提出的DT_aPRE_HVE方案是首个通过引入指定验证者来抵御离线关键词测试攻击的HVE加密策略.尽管有许多PEKS加密方案，如文献[18-19]，通过指定验证者来抵御KG攻击，目前尚无HVE方案考虑KG攻击这一问题.而由于在EHR系统中，关键词集合可能只在特定的医学术语中产生，因此，能够抵御KG攻击就对HVE方案在EHR系统中的应用具有重要意义.

3) 与已有的支持指定验证者或代理重加密功能的PEKS和HVE方案相比，本文方案的计算和通信复杂度均较低.具体地，本文方案的搜索令牌空间复杂度为O(1)，验证算法的双线性对运算次数为O(1)，重加密算法的时间复杂度也限定在O(1)常数上限内.

4) 本文提出的DT_aPRE_HVE方案在标准模型下面对选择密文、选择时间攻击是可证明安全的.同时，基于扩展判定线性假设(augmented decision linear assumption)可以证明方案在标准模型下面对离线关键词测试攻击也是可证明安全的.

1 相关工作

1.1 谓词加密PE与隐藏向量加密HVE

在谓词加密方案中，主密钥的拥有者可以为特定谓词集合中的任意谓词向量P生成相应的解密密钥skP.如果密文的关联属性为向量x，则当且仅当P(x)=1时，skP才可以解密密文.关于谓词加密方案目前已经有很多研究成果，如文献[20-24].其中，Katz等人[20]提出的谓词加密策略可以很好地支持关键词合取、析取和内积等操作.然而，所有这些谓词加密策略均需要至少O(l)次的双线性对运算来执行一次解密或验证操作，令牌的空间复杂度也为O(l)(l为查询向量的维数)，因此方案的效率较低.

HVE加密作为谓词加密的一种，由Boneh和Waters[25]在2007年首次提出.在HVE加密策略中，密文关联的属性定义为字母表Σ上的向量x=(x1,x2,…,xl)，查询向量定义为字母表Σ*=Σ∪{*}上的σ=(σ1,σ2,…,σl).当且仅当向量x与σ匹配时，才可以检索密文.Boyen[26]基于合数阶双线性群假设证明了提出的HVE方案的安全性.然而，基于合数阶双线性群的HVE方案的渐进性复杂度较高.针对这一问题，Park等人[27-28]提出了2个HVE策略，将方案的双线性对运算次数和搜索令牌的空间复杂度限定在了常数范围内，提高了HVE方案的执行效率.文献[29-30]也提出了同样高效的HVE方案.然而，这些方案均无法在保证较低的渐进性复杂度的同时，有效地抵御离线关键词测试攻击并支持代理重加密功能，影响了方案的实际应用性.

1.2 离线关键词测试攻击

离线关键词测试攻击KG，也称为字典攻击.当关键词取值集合的空间复杂度与搜索令牌的熵较小时，攻击者就可以实施KG攻击，而一旦攻击者通过枚举或猜测建立了令牌与关键词之间的映射关系，就可以威胁整个加密方案的安全性.一种解决KG攻击的方法是指定验证者来执行验证算法，防止攻击者直接判断令牌和密文的匹配程度，如文献[31-33].然而，这些方案均无法支持关键词合取或集合运算，方案的计算复杂度也较高.

1.3 支持代理重加密功能的可搜索加密策略

代理重加密机制通过引入一个代理服务器，将原始密文转化为代理者可以访问的重加密密文.Shi与Waters在文献[34]中考虑了如何将代理重加密机制与谓词加密策略进行合并，并进而提出了支持代理重加密的HVE加密机制.在文献[34]中，通过将搜索令牌经代理服务器进行分发共享来赋予代理用户访问密文的权限.但是他们的方案依然基于合数阶双线性群，因此计算和存储的开销较大.而且令牌的共享机制除了需要额外的安全信道外，也难以及时的撤销过期的访问权限.同样支持代理重加密功能的还有文献[35-37]提出的PEKS方案，但这些方案均不能高效地撤销代理权限，且不能支持多关键词搜索.Wang等人[38]提出了支持关键词合取搜索且具有代理重加密能力的PEKS方案，但是该方案仅在随机预言模型下是可证明安全的.在实际应用中，很难保证诸如Hash函数等对象可以按照在随机预言证明中所假设的那样，实现完全的随机化，从而难以保证系统的实际安全性[39].文献[10]利用授权矩阵方式动态地分配代理权限，然而方案无法支持多关键词检索，限制了方案的实用性.文献[15-17]通过引入时间戳来实现细粒度的权限控制.与文献[10,35-38]提出的方案相比，基于时间的代理访问控制可以高效的实现代理权的撤销，且不同代理者之间互不影响，达到了用户级的权限管理.然而这些方案无法支持密文检索.针对时间可控的代理访问与可搜索加密结合的问题，Yang等人[14]基于PEKS方案，通过引入额外的时间服务器，使得数据拥有者可以更加自由地控制密文的访问权限.同时，文献[14]采用基于延迟加密的重加密策略[40]以减轻代理服务器的运行负荷.然而，额外的时间服务器会增加系统的复杂度，也带来了更多的安全隐患.而且文献[14]的方案的通信和计算复杂度均较高，需要至少O(l)次的双线性对运算来执行一次验证操作，搜索令牌的大小也是O(l)，重加密过程也需要额外的O(l)次的指数运算.

1.4 系统模型

在传统的PEKS系统中，一般定义4种类型的通信实体:1)可信的第三方服务器(trusted third party, TTP)为各方实体生成密钥;2)数据拥有者(data owner)将数据与关键词集合分别加密后上传到服务器;3)数据访问者(data user)生成搜索令牌并发起搜索请求;4)半诚实的服务器执行令牌与密文的匹配验证操作，返回相应的密文搜索结果.

本文在传统的PEKS系统的基础上增加了代理服务器(proxy server, PS)，如图1所示：

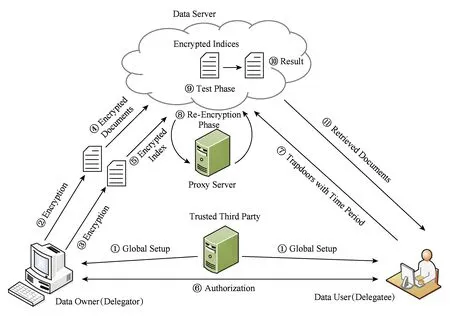
Fig. 1 DT_aPRE_HVE system model图1 DT_aPRE_HVE系统模型

与文献[14]中的方案不同，本文方案不需要额外的时间服务器来生成时间戳，而是在授权过程中嵌入时间戳.具体地，在文献[14]中，当数据拥有者发起授权操作时，需要同时给代理服务器和时间服务器发送通知，时间服务器根据数据拥有者的要求，利用自身的密钥生成时间戳，并将时间戳发送给代理者以供其生成合法的搜索令牌.额外的时间服务器不仅增加了系统的复杂度，也增加了安全风险.然而在本文方案中，时间戳被封装在授权密钥中，由TTP生成.在授权阶段，数据拥有者为TTP生成一份代理人和时间区间的列表，而TTP通过特定的授权算法为列表中的每个代理者生成包含各自时间区间的授权密钥.在重加密阶段，代理服务器依据数据拥有者指定的时间区间重加密密文.代理者利用自身的密钥以及TTP发送的授权密钥生成搜索令牌.当服务器验证查询向量与密文属性相匹配，且搜索令牌与重加密密文中的时间区间相匹配时，返回相应检索结果.

本文系统的安全性基于2个假设：1)服务器不会实施离线关键词测试攻击；2)服务器不会与外部攻击者进行合谋攻击.事实上，文献[14,31-33]等方案的安全性也基于这2个前提.本文考虑2种类型的敌手模型:1)半诚实的服务器端，其会在诚实的执行搜索操作的同时，试图获取用户的敏感数据；2)外部攻击者，通过窃听通信信道上的传输数据来试图分析用户的私有信息.与文献[14-17]中的安全模型不同的是，本文在安全游戏的挑战阶段之后，允许敌手进行关于挑战密文的重加密问询(显然重加密的目标身份不可以是敌手自己)，并证明了重加密密文依然满足属性隐藏性，因此方案的安全性更高.与此同时，本文也考虑了离线关键词测试攻击问题，并在安全分析中证明了搜索令牌可以完全隐藏查询向量的信息，从而使敌手无法建立关键词与令牌之间的映射关系，达到抵御离散关键词测试攻击的目的.

2 DT_aPRE_HVE的形式化定义与安全模型

2.1 预备知识

标识与记号：设q为正素数，q表示范围内的整数，*q=q{0}.‖v‖2表示向量v的l2范数.|S|表示集合S中元素个数.本文中使用标准的O记号表示函数的复杂度上界，即g(n)=(f(n))当且仅当存在正常数c和n0，使得对任意的n≥n0有|g(n)|≤c|f(n)|成立.相应地，定义下界复杂度记号ω，即g(n)=ω(f(n))当且仅当存在正常数c和n0，使得对任意的n≥n0有|g(n)|≥c|f(n)|成立.表示x随机取自集合S.定义关于n的可忽略函数negl(n)，使得对任意多项式g(n)，当n足够大时都有如果概率p=1-negl(n)则称概率是压倒性成立的，若p=negl(n)，则称概率是可忽略的.对于向量xb∈{0,1}l，记xbi∈{0,1}为xb的第i位.

当且仅当fσ(x)=1时，称x与σ匹配.

定义2. 双线性映射[14].设G与GT分别为阶为素数p的循环群，g∈G为群G的生成元.则双线性映射e:G×G→GT成立当且仅当：

1) 双线性性.对任意u,v∈G，a,b∈，有e(ua,vb)=e(u,v)ab.

2) 非退化性.e(g,g)≠1.

3) 可计算性.存在有效的多项式时间算法计算映射e.

定义3. 复杂性假设[27]：

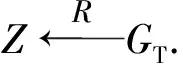
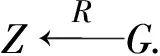
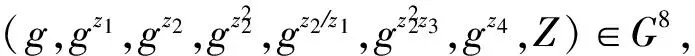
2.2 DT_aPRE_HVE的形式化定义

本文提出的支持指定验证者和可撤销代理重加密的DT_aPRE_HVE方案包含11个多项式时间算法:

1) 系统建立Setup(k).由TTP执行，输入安全参数k，输出主公钥Mpk与主密钥Msk.

2) 用户密钥生成KGuser(Mpk,Msk).设用户集user={user0,user1,…,usern},n为用户数.由TTP执行，输入Mpk和Msk，生成用户密钥对[pkuser,skuser].

3) 服务器密钥生成KGserver(Mpk,Msk).由TTP执行，输入Mpk和Msk，生成服务器密钥对[pkserver,skserver].

4) 令牌生成算法Trap(pkserver,pkuser,skuser,Mpk,σ).由数据访问者执行，输入pkserver,pkuser,skuser,Mpk以及查询向量σ，输出查询令牌TKσ.

5) 加密算法Enc(pkserver,pkuser,skuser,Mpk,x).由数据拥有者执行，输入pkserver,pkuser,skuser,Mpk以及属性向量x，输出密文CT.

6) 验证算法Test(CT,TKσ,skserver).由服务器执行，输入CT,TKσ,skserver，若fσ(x)=1，输出1，否则输出0.

7) 授权算法Autuser0→user1(skserver,pkuser0,skuser0,pkuser1,skuser1,T).由TTP执行，输入skserver,pkuser0,skuser0,pkuser1,skuser1以及时间区间T，其中pkuser0,skuser0与pkuser1,skuser1分别为用户user0与user1的密钥对，且user0作为数据拥有者向代理者user1授权.输出授权密钥akuser0→user1.

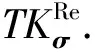
9) 重加密密钥生成算法Re_KGuser0→user1(skserver,pkuser0,skuser0,pkuser1,skuser1).由TTP执行，输入skserver,pkuser0,skuser0,pkuser1,skuser1，输出重加密密钥rkuser0→user1.

10) 重加密算法Re_Enc(rkuser0→user1,CT,T).由代理服务器执行，输入rkuser0→user1,CT,T，输出重加密密文CTRe.

2.3 安全模型

定义4. 选择消息、选择时间攻击的不可区分性(indistinguishable against chosen keyword chosen time attack, IND-CKCTA).如果概率多项式时间(probabilistic polynomial time, PPT)的敌手A赢得以下游戏Game的概率是可忽略的，则称本文提出的DT_aPRT_HVE方案是IND -CKCTA安全的.

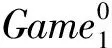
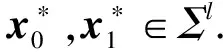
2) 系统建立Setup.输入安全参数k，挑战者C运行方案的Setup(k)算法生成主密钥对Mpk,Msk，同时运行KGuser(Mpk,Msk)和KGserver(Mpk,Msk)生成用户和服务器的密钥对.若b=1，C将{Mpk,pkuser,pkserver,skserver}发送给AServer；否则，C将{Mpk,pkuser,skuser,pkserver}发送给Ae.

3) 敌手适应性的进行如下问询.

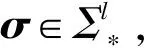
Ae由于拥有自己的密钥因此不需要进行令牌或代理令牌问询.

③ 授权密钥问询.当b=2时，Ae提交身份对user0,user1，时间区间T，C返回授权密钥akuser0→user1.

④ 重加密密钥问询.敌手A提交身份对user0,user1，C返回重加密密钥rkuser0→user1.

⑤ 重加密问询.敌手A提交身份对user0,user1，原始密文CT，时间区间T，C返回重加密密文CTRe.

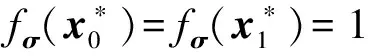
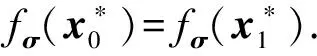
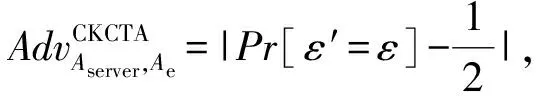
定义5. 针对离线关键词测试攻击的不可区分性(indistinguishable against keyword guessing attack, IND-KGA).如果PPT敌手A赢得以下游戏Game3的概率是可忽略的，则称本文方案面对离线关键词测试攻击是IND-KGA安全的.

Game3：

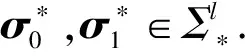
2) 系统建立Setup.输入安全参数k，挑战者C运行方案的Setup(k)算法生成主密钥对Mpk,Msk，同时运行KGuser(Mpk,Msk)和KGserver(Mpk,Msk)生成用户和服务器的密钥对.C将{Mpk,pkuser,pkserver}发送给A.

3) 敌手适应性的进行如下问询.

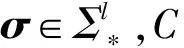
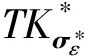
3 DT_aPRE_HVE方案的具体实现

本节给出DT_aPRE_HVE方案的具体实现.方案包括11个多项式时间算法.

1) 系统建立Setup(k).由TTP执行.设g∈G为循环群G的生成元，算法随机取整数v1,v2,…,vl;t1,t2,…,tl∈p.算法随机选取群元素a1,a2,…,al;b1,b2,…,bl;c1,c2,…,cl∈G.对每个i∈{1,2,…,l}，设Vi=gvi，Ti=gti.H:{0,1}*→p为TTP任意选定的抗碰撞Hash函数.算法输出主密钥对：

2) 用户密钥生成KGuser(Mpk,Msk).由TTP执行.算法随机选取y1,y2,α,β,ε∈p，设Y1=gy1,Y2=gy2，输出用户的密钥对：pkuser={Y1,Y2,Ω,gε}，skuser={y1,y2,α,β,ε}，其中Ω=e(gα,Y1)e(gβ,Y2).

3) 服务器密钥生成KGserver(Mpk,Msk).由TTP执行.设s,τ∈输出服务器密钥对pkserver=gs，skserver=s,τ.

4) 令牌生成算法Trap(pkserver,pkuser,skuser,Mpk,σ).由数据访问者执行，设S(σ)={i|σi≠*}，算法随机选择A,B,C∈p，(ri,ki),(ηi,τi),(mi,ni)∈p，且对于i∈S(σ)均有riy1+kiy2=A，ηiy1+τiy2=B，miy1+niy2=C，则算法输出搜索令牌如下：

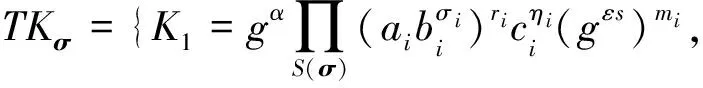
其中,Δ=|S(σ)|.

5) 加密算法Enc(pkserver,pkuser,skuser,Mpk,x).由数据拥有者执行，x=(x1,x2,…,xl)∈(Σ)l为密文关联的关键词属性，算法随机选取s1,s2∈p，输出密文：

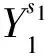
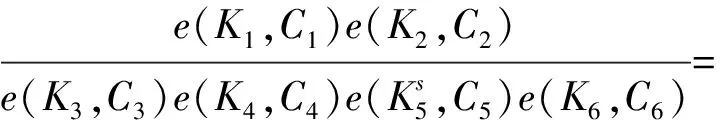
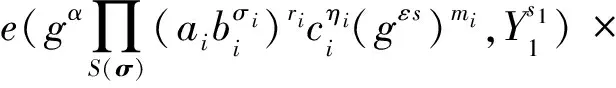
因此，若fσ(x)=1，Test(CT,TKσ,skserver)=1，否则算法输出0.

7) 授权算法Autuser0→user1(skserver,pkuser0,skuser0,pkuser1,skuser1,T).由TTP执行，设pkuser0={Y0,1,Y0,2,Ω0,gε0}，skuser0={y0,1,y0,2,α0,β0,ε0}为用户user0的密钥对，pkuser1={Y1,1,Y1,2,Ω1,gε1}，skuser1={y1,1,y1,2,α1,β1,ε1}为用户user1的密钥对.设user0为数据拥有者，通过TTP向代理者user1发起授权，T由user0指定.则授权密钥akuser0→user1为

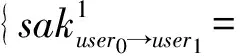
8) 代理令牌生成算法Re_Trap(pkserver,pkuser1,skuser1,Mpk,σ,akuser0→user1).由代理数据访问者user1执行，算法随机选择A1,B1,C1∈p，(r1,i,k1,i),(η1,i,τ1,i),(m1,i,n1,i)∈p，且对于i∈S(σ)有r1,iy1,1+k1,iy1,2=A1，η1,iy1,1+τ1,iy1,2=B1，m1,iy1,1+n1,iy1,2=C1，算法输出如下：

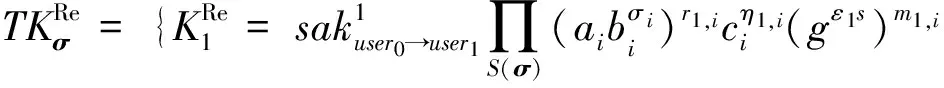
其中,Δ=|S(σ)|.

10) 重加密算法Re_Enc(rkuser0→user1,CT,Tc).由代理服务器执行，时间区间为Tc(user0指定)，生成重加密密文：

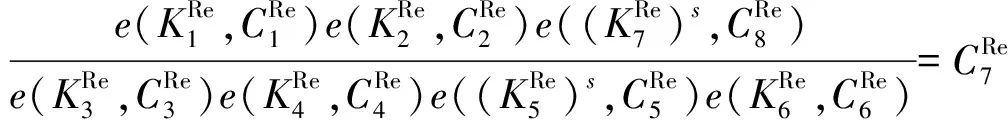
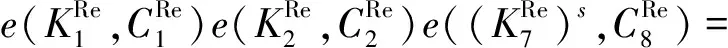
同时有:

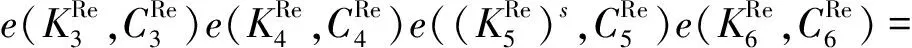
提出的DT_aPRE_HVE方案的验证算法依赖于2个条件，分别是fσ(x)以及T,Tc是否匹配.数据拥有者通过授权密钥的方式将T隐式地发送给代理者用于代理令牌的生成.在重加密过程中，可以将Tc嵌入到密文中，实现访问控制.在fσ(x)=1的前提下，所有T=Tc的代理用户都可以访问密文，同时，数据拥有者也可以为不同时间区间的用户，如T1,T2,…,Tn，分别生成对应的时间区间为Tc1,Tc2,…,Tcn的重加密密文，且互不影响.即使数据拥有者处于离线模式，代理权限依然可控.同时，DT_aPRE_HVE方案的代理令牌生成和重加密算法只需要O(1)次指数运算，较之文献[14]中O(l)次指数运算，可以更高效地支持这种细粒度的重加密策略.

4 DT_aPRE_HVE方案的安全证明

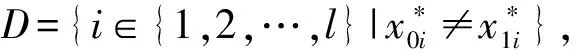
在证明IND-CKCTA安全性方面，首先定义一系列混合游戏如下：

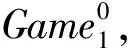
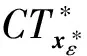
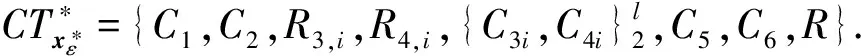
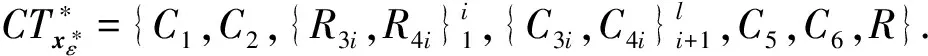
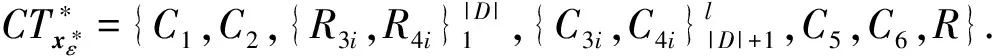
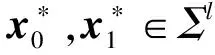
在具体证明之前，定义3种类型的搜索令牌或代理令牌问询，以及2种类型的授权密钥问询.

1) 搜索令牌或代理令牌问询方面

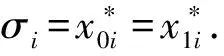
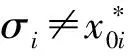
2) 授权密钥问询方面

类型1. 此时Ae作为授权发起方，在授权密钥问询中作为user0.

类型2. 此时Ae作为被授权方，在授权密钥问询中作为user1.

定理1. 若BDH假设以及ADLP假设在循环群G中成立，则所提出的DT_aPRE_HVE方案在标准模型下是IND-CKCTA安全的.

定理1可以通过4个引理进行证明.引理1和引理2证明方案面对半诚实服务器的IND-CKCTA安全性.引理3和引理4证明方案面对恶意外部敌手的IND-CKCTA安全性.

证明. 设挑战者为C，构造C与Aserver之间的概率多项式时间算法B如下:

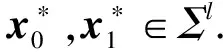
2) 系统建立Setup.算法随机选取r1,r2,y1,y2,v1,v2,…,vl,t1,t2,…,tl,θ1,θ2,…,θl,φ1,φ2,…,φl,λ1,λ2,…,λl以及s,ε,τ∈p.若y1+y2=0，则重新选择y1,y2.C设置Y1=gy1,Y2=gy2.对任意i∈[1,l]，设将参数集合给敌手Aserver，注意，对C与Aserver来说，α=ab+r1与β=ab+r2均是未知的.这里假设skuser={y1,y2,ε,α,β}是某个用户userx的密钥.

3) 敌手适应性地进行如下问询.

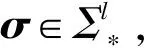
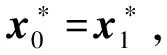
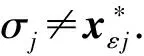
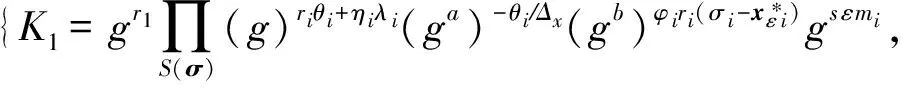
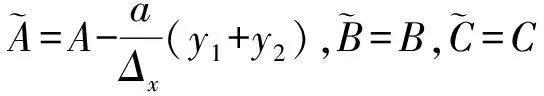
Ⅰ 若user0≠userx，C调用方案的KGuser(Mpk,Msk)算法生成user0和user1的密钥，再调用方案的Autuser0→user1和Re_Trap算法正常生成代理令牌并发送给Aserver.

Ⅱ 若user0=userx，C回答敌手Aserver:

类型1. 与①一样，B随机输出{0,1}并退出，此时Game0恰为Game1.

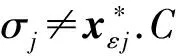
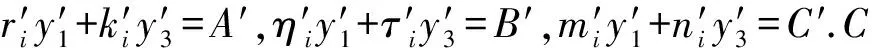
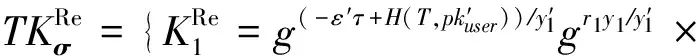
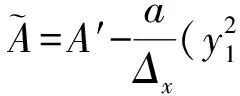
③ 重加密密钥问询.敌手Aserver提交身份对user0,user1，C调用KGuser(Mpk,Msk)算法生成user0和user1的密钥，之后调用Re_KGuser0→user1算法返回重加密密钥rkuser0→user1并发送给Aserver.

④ 重加密问询.敌手Aserver提交身份对user0,user1以及原始密文CT，时间区间Tc，C首先进行重加密密钥问询获得rkuser0→user1，之后调用方案的Re_Enc算法生成重加密密文CTRe.

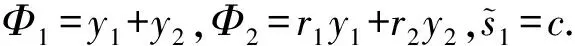
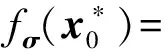
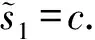
6) 猜测Guess.敌手Aserver输出猜测ε′，若ε′=ε，B输出1，否则输出0.

证毕.

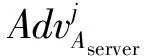
证明. 设挑战者为C，构造C与Aserver之间的概率多项式时间算法B如下：

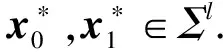
2) 系统建立Setup.设Dj+1=δ，算法随机取r1,r2,y1,y2,v1,v2,…,vl,t1,t2,…,tl,θ1,θ2,…,θl,φ1,φ2,…,φl,λ1,λ2,…,λl以及s,τ,w∈p，且其中和对挑战者C不可见，对任意i∈[1,l]且i≠δ，设对i=δ，有令Ω=e(gr1,Y1)e(gr2,Y2)，C将参数集合发送给敌手Aserver.

3) 敌手适应性的进行如下问询.

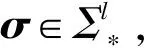
类型1. 此时δ∉S(σ)，C随机选择A,B,C∈p，(ri,ki),(ηi,τi),(mi,ni)∈p，且对任意i∈S(σ)，riy1+kiy2=A，ηiy1+τiy2=B，miy1+niy2=C，C返回TKσ：

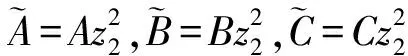
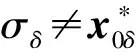
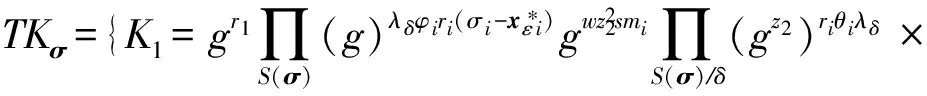
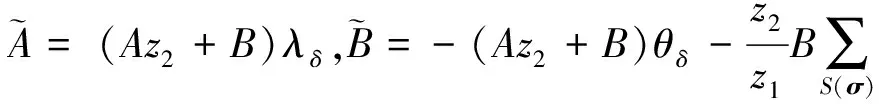
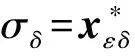
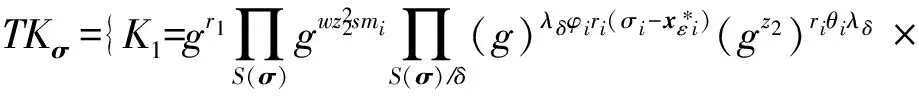
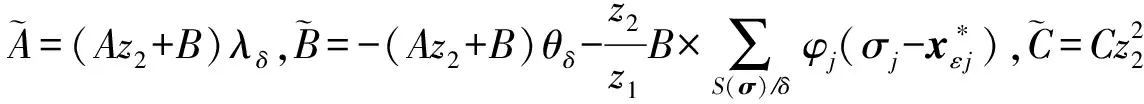
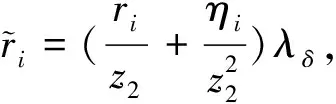
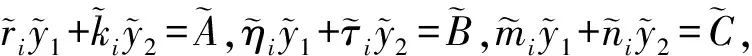
③ 重加密密钥问询.敌手Aserver提交身份对user0,user1，C调用KGuser(Mpk,Msk)算法生成user0和user1的密钥，之后调用Re_KGuser0→user1算法返回重加密密钥rkuser0→user1并发送给Aserver.

④ 重加密问询.敌手Aserver提交身份对user0,user1以及原始密文CT，时间区间Tc，C首先进行重加密密钥问询获得rkuser0→user1，之后调用方案的Re_Enc算法生成重加密密文CTRe.

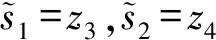
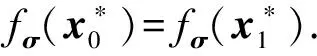
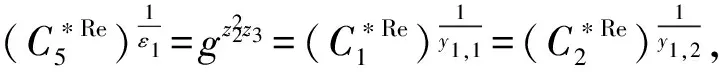
6) 猜测Guess.敌手Aserver输出猜测ε′，若ε′=ε，B输出1，否则B输出0.

证毕.

证明. 设挑战者为C，构造C与Ae之间的概率多项式时间算法B.

2) 系统建立Setup.算法随机选取整数r,αe,βe,r1,r2,y1,y2,ye,1,ye,2，v1,v2,…,vl,t1,t2,…,tl,以及θ1,θ2,…,θl,φ1,φ2,…,φl,λ1,λ2,…,λl∈p，s,εe,ε,τ∈p，若y1+y2=0或ye,1+ye,2=0，则重新选择y1,y2或ye,1,ye,2.设Y1=gy1,Y2=gy2,Ye,1=gye,1,Ye,2=gye,2，对任意i∈[1,l]，设将参数ye,1,ye,2以及集合发送给Ae.相当于pkAe={Ye,1,Ye,2,Ωe,gεe}，skAe={ye,1,ye,2,αe,βe,εe}.

3) 敌手适应性地进行如下问询.

① 授权密钥问询.Ae提交身份对user0,user1与时间区间T.若user0≠Ae且user1≠Ae，算法直接调用KGuser(Mpk,Msk)生成user0,user1的密钥并调用Autuser0→user1生成授权密钥akuser0→user1返回敌手.否则.

② 重加密密钥问询.敌手Ae提交身份对user0,user1，C调用KGuser(Mpk,Msk)算法生成user0和user1的密钥，之后调用Re_KGuser0→user1算法返回重加密密钥rkuser0→user1并发送给Ae.

③ 重加密问询.敌手Ae提交身份对user0,user1以及原始密文CT，时间区间Tc，C首先进行重加密密钥问询获得rkuser0→user1，之后调用方案的Re_Enc算法生成重加密密文CTRe.

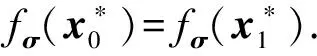
6) 猜测Guess.敌手Ae输出猜测ε′，若ε′=ε，B输出1，否则输出0.

证毕.

证明. 设挑战者为C，构造C与Ae之间的概率多项式时间算法B如下：

2) 系统建立Setup.设Dj+1=δ，算法随机取r,y1,y2,αe,βe,r1,r2,ye,1,ye,2,v1,v2,…,vl，t1,t2,…,tl以及θ1,θ2,…,θl,φ1,φ2,…,φl,λ1,λ2,…,λl，s,w,εe,τ∈p.设对任意i∈[1,l]且设将参数ye,1,ye,2以及集合发送给Ae.相当于pkAe={Ye,1,Ye,2,Ωe,gεe}，skAe={ye,1,ye,2,αe,βe,εe}.

3) 敌手适应性的进行如下问询.

① 授权密钥问询.与引理3中的授权密钥问询一样.

② 重加密密钥问询.与引理3中的重加密密钥问询一样.

③ 重加密问询.与引理3中的重加密问询一样.

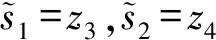
6) 猜测Guess.敌手Ae输出猜测ε′，若ε′=ε，B输出1，否则输出0.

证毕.

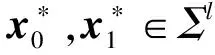
定理2. 设ADLP假设在循环群G中成立，则所提出的DT_aPRE_HVE方案在标准模型下是IND-KGA安全的.

证明. 设挑战者为C，构造C与A之间的概率多项式时间算法B如下：

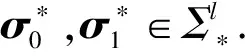
2) 系统建立Setup.算法随机选取r1,r2,y1,y2,φ1,φ2,…,φl,λ1,λ2,…,λl,τ∈p，设由此可知隐式成立.对于任意将参数集合发送给敌手A.

3) 敌手适应性的进行如下问询.

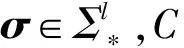
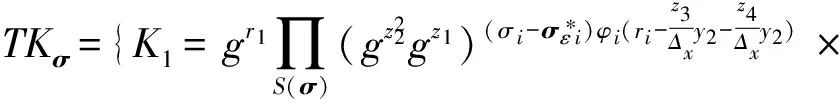
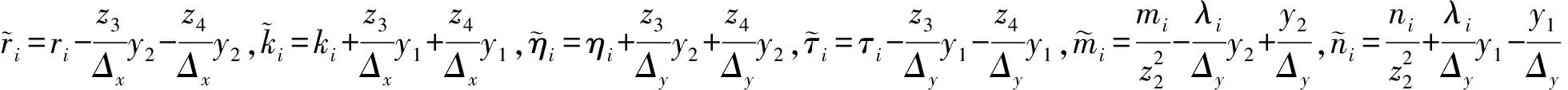
4) 挑战阶段Challenge.挑战者输出挑战令牌：

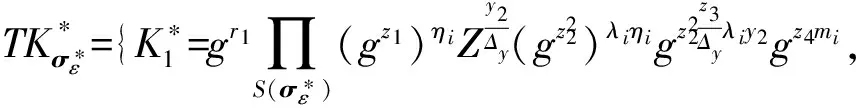
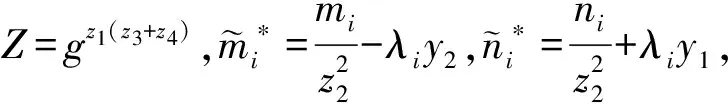
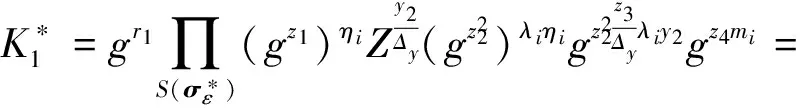
且同理：

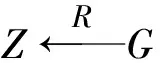
6) 猜测Guess.敌手猜测输出ε′，若ε′=ε，B输出1，否则输出0.

证毕.

5 DT_aPRE_HVE方案的效率分析

本节将所提出的DT_aPRE_HVE方案与其他典型的PEKS或HVE方案，如文献[13-17,21-24,27-33,35-38]进行安全性、渐进性复杂度(时间和空间复杂度)以及算法执行效率等方面的对比.

方案的安全性对比如表1所示：

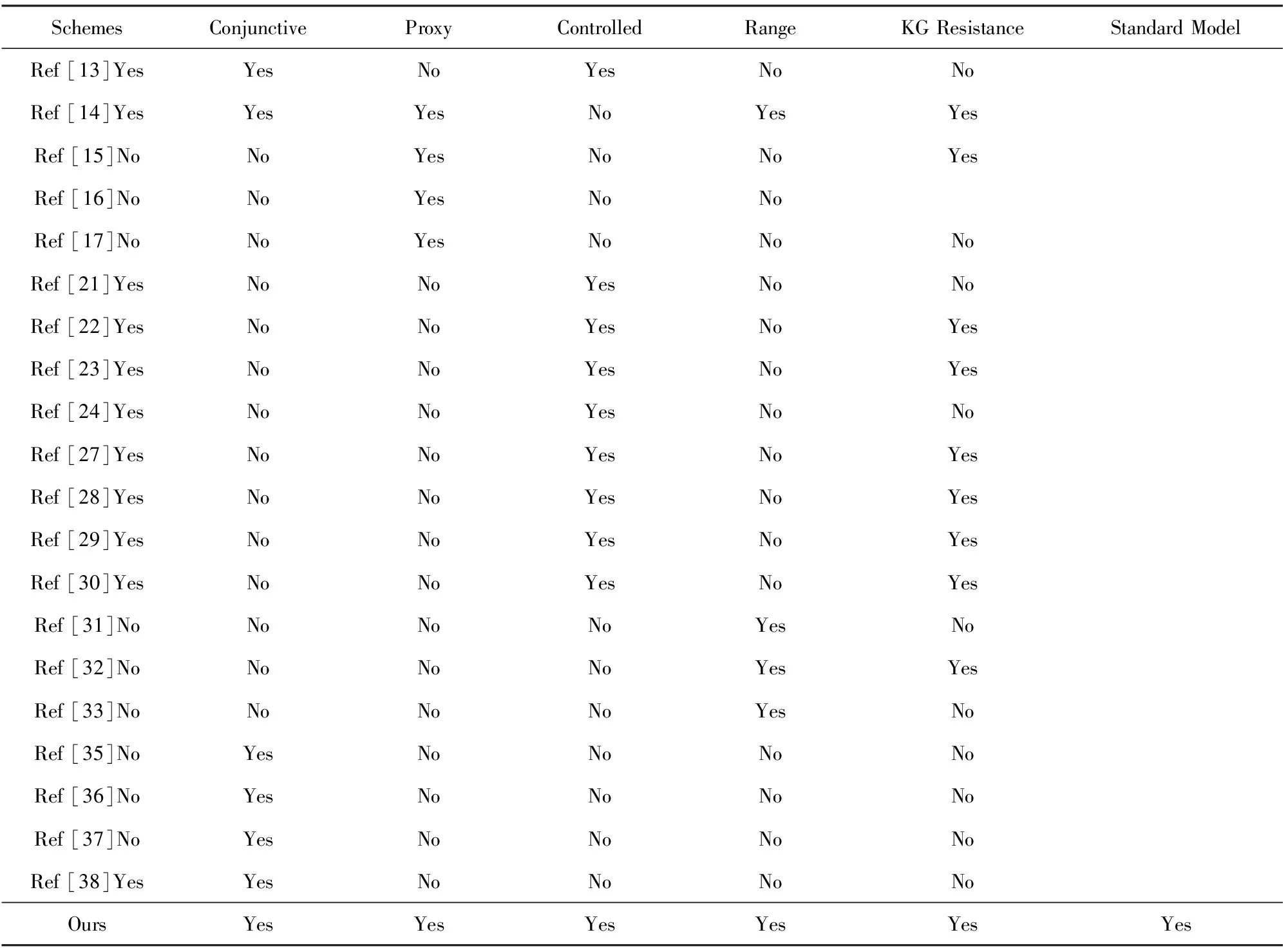
Table 1 Comparison of Security of PEKS and HVE Schemes表1 PEKS方案与HVE方案的安全性对比

由表1可以看出，本文提出的DT_aPRE_HVE方案是第1个具有可撤销重加密代理功能并抵御KG攻击的HVE方案.尽管有许多PEKS方案可以支持代理重加密功能，但这些方案只能进行单关键词查询，这在实际应用中，尤其是EHR等环境下并不可行.文献[14，38]支持合取关键词查询与可控的代理重加密功能，然而文献[14]无法支持范围查询，文献[38]则只在随机预言模型下是可证明安全的.其余的HVE方案基本没有考虑到KG攻击问题，而在EHR环境中，由于关键词集合较小，抵御KG攻击的能力对于方案的应用具有重要意义.因此，本文方案的实际应用安全性更高.

设te为一次指数运算的时间，tp为一次双线性对运算的时间，l为查询向量的维数，|S(σ)|为S(σ)集合的大小.s1,s2分别为群G,GT中元素的大小.忽略整数的空间占用、乘法运算和Hash函数运算时间.方案的空间和时间复杂度对比分别如表2和表3所示.

由表2和表3可以看出，只有本文提出的DT_aPRE_HVE方案的原始令牌或代理令牌的空间复杂度均为O(1).尽管文献[15,17]以及文献[27-30,32-33,35-37]的令牌尺寸也为O(1)，但是其要么无法支持合取关键词搜索，要么无法撤销代理者权限.在公钥或私钥尺寸方面，尽管文献[14-17,31,33,35-37]优于本文方案,但是文献[14]的令牌尺寸为O(l)，私钥尺寸与本文一样也为O(l)，且文献[15-17,31,33]无法支持代理重加密，文献[31,33,35-37]只允许单个关键词搜索.在加密算法、重加密算法、令牌生成算法和验证算法方面，本文的时间复杂度优于文献[13-14]提出的方案.与文献[15,17,27,32-33,35-37]相比，本文的加密算法时间复杂度较高，这主要是由于文献[15,17,27,32-33]不需要支持代理重加密，而文献[35-37]不需要支持多关键词检索且代理权限不可撤销，从而减少了额外的计算开销.综合来看，本文方案在实现了合取关键词检索和可撤销的代理重加密的基础上，保证了较低的渐进性复杂度，具有更好的实用性.

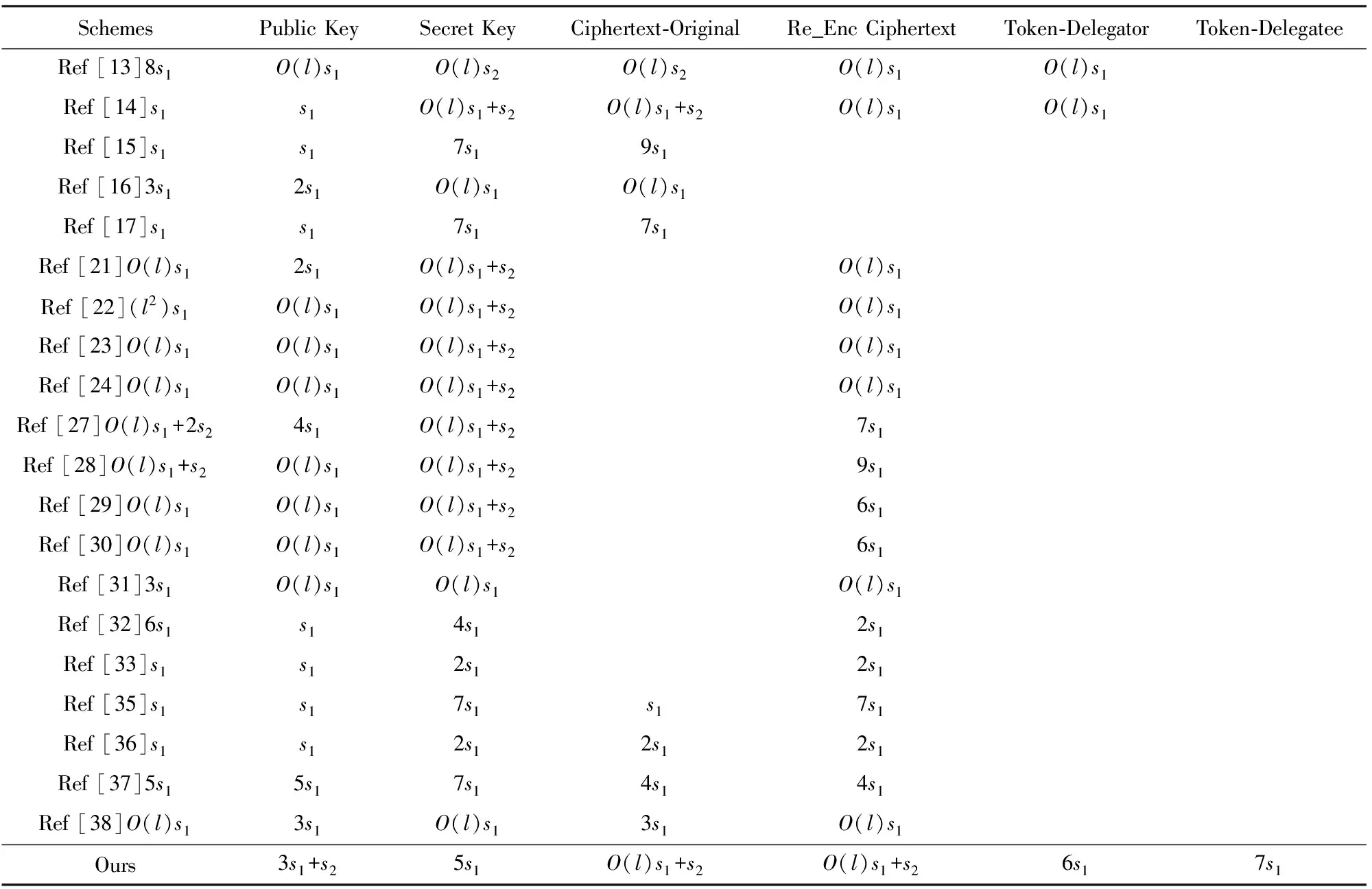
Table 2 Comparison of Space Complexity of PEKS and HVE Schemes表2 PEKS方案与HVE方案的空间复杂度对比

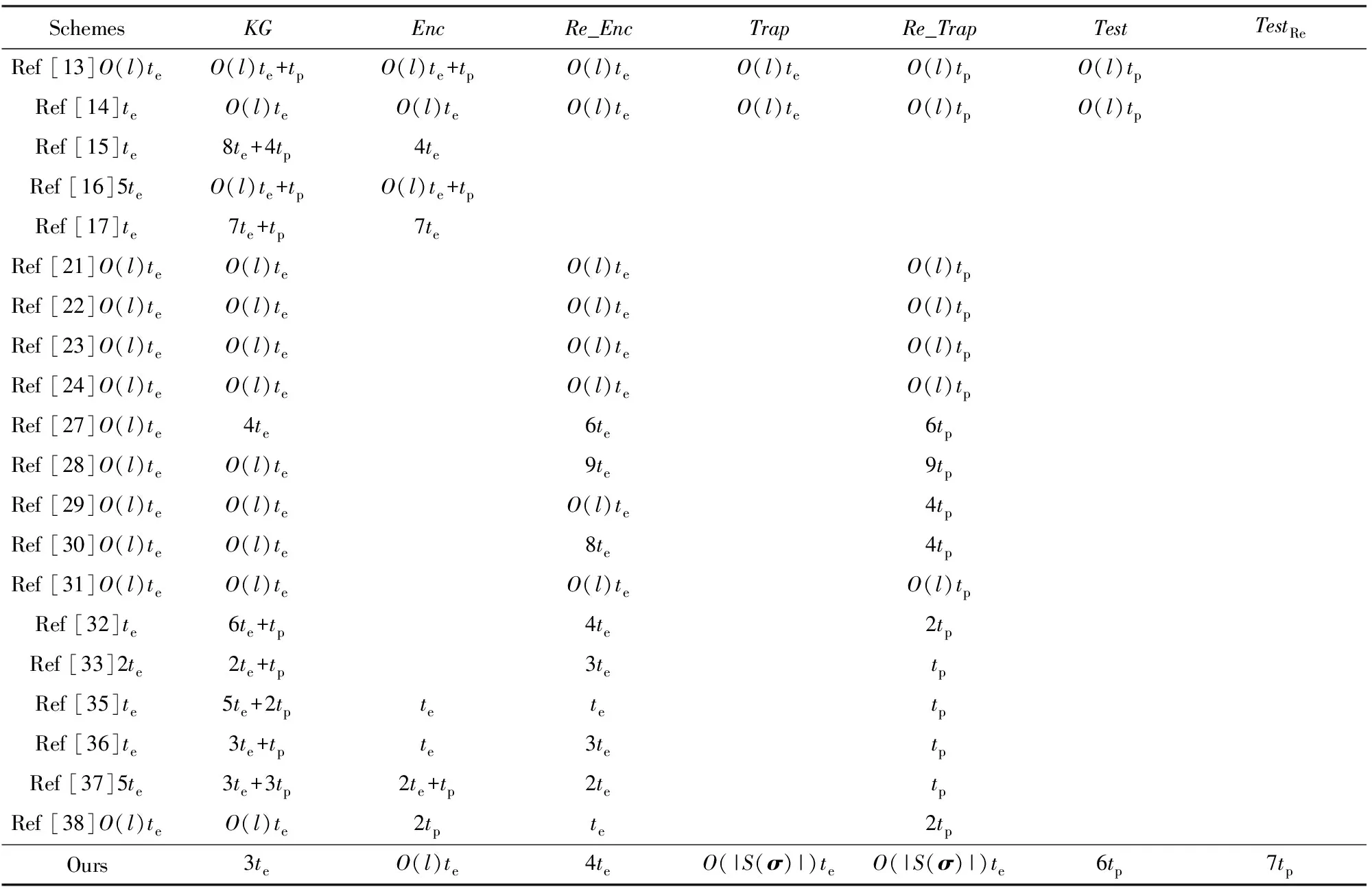
Table 3 Comparison of Time Complexity of PEKS and HVE Schemes表3 PEKS方案与HVE方案的时间复杂度对比

在效率对比方面，本文只选取了文献[13-14]作为对比对象，主要原因是文献[13]与本文方案均基于HVE方案，对比度较高，而文献[14]同样支持可撤销的代理重加密功能.虽然文献[38]也支持代理重加密，但是由于其既不支持合取关键词搜索，也无法撤销代理权限，因此不作为对比对象.本文主要对比Enc,Trap,Test等算法以及针对代理者的Re_Enc,Re_Trap,TestRe算法.本文选择了与文献[14]一样的模拟环境，利用PBC(pair-based cryptography Library)函数库，群G,GT的阶也为160 b，仿真对比结果如图2所示:

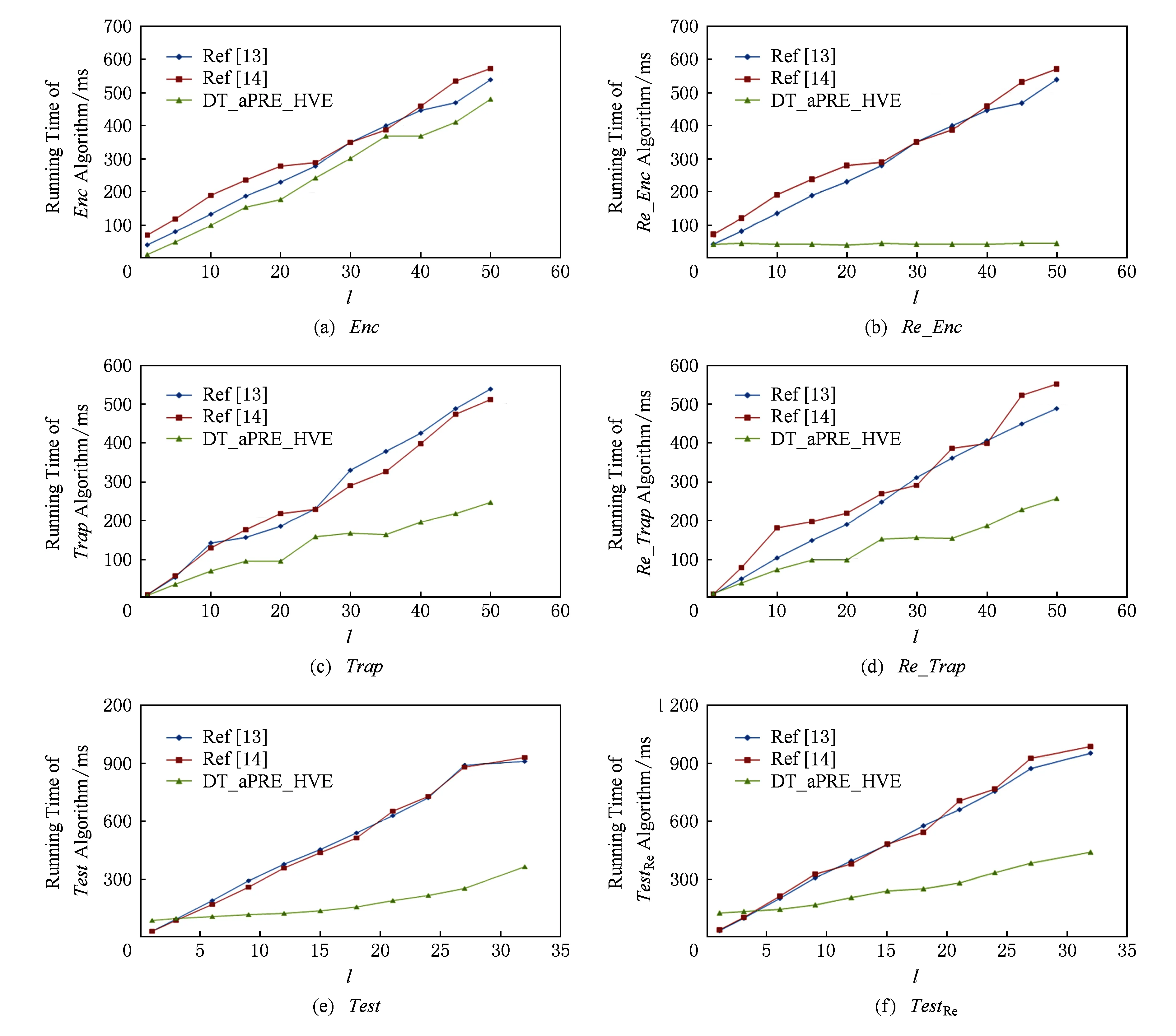
Fig. 2 Comparison of Efficiency of the Proposed Scheme and the Schemes in Ref [13] and Ref [14]图2 本文方案与文献[13]、文献[14]的算法效率对比

从图2可以看出，本文方案在算法的执行效率上优于文献[13-14]的方案.主要原因是本文方案在Test,TestRe算法中只需要O(1)次双线性对运算，而文献[13-14]均需要O(l)次.本文方案的Test,TestRe算法依然依赖于查询向量维数l，需要O(|S(σ)|)次的乘法运算，但对比O(l)次的双线性对运算，时间有所降低，且文献[103-14]同样需要额外O(l)次的乘法运算.在加密算法Enc中，DT_aPRE_HVE方案不需要双线性对运算，而文献[13]需要额外1次双线性对运算.在重加密算法Re_Enc方面，文献[13-14]均需要额外的O(l)次指数运算，本文方案只需要4次指数运算.在令牌生成算法Trap,Re_Trap方面，本文方案依赖于O(|S(σ)|)，显然有O(|S(σ)|)≤O(l)≤O(l2).因此，本文方案在应用效率方面较文献[13-14]有所提高.

6 结束语

本文基于隐藏向量加密(HVE)提出了支持指定验证者与可撤销代理重加密的加密搜索方案DT_aPRE_HVE.在安全性方面，本文方案可以有效地抵御外部攻击者实施的离线关键词测试攻击.同时，本文采用将时间戳嵌入到授权密钥中的方法，在不需要额外的时间服务器的基础上实现了用户级的细粒度的代理权限管理.在效率方面，本文方案搜索令牌的空间复杂度、重加密算法和验证算法的双线性对运算次数均限定在了常数上限内.因此，较之已有的具有多关键词搜索和代理重加密功能的可搜索加密方案，本文方案具有较好的实用价值.

本文方案存在2点可以改进的地方:1)在密文空间复杂度和加密算法的时间复杂度方面，本文方案线性依赖于查询向量的维数.2)在验证算法中，虽然双线性对运算次数为常数，但需要O(|S(σ)|)次的乘法运算，尽管相比于O(l)次的双线性对运算，效率有所提高，但依然可以改进优化.此外，目前的谓词加密策略和隐藏向量加密策略还无法有效的支持排序搜索.一种解决方法是将关键词和密文的词频、逆词频关系嵌入到验证算法中，在验证查询向量和属性向量是否匹配的同时计算匹配程度，进而实现排序检索.然而由于验证算法大多数基于双线性对运算，较难构造具有单调性的函数，导致验证结果的比较成为一个研究难点.因此，下一步的研究重点将集中在构建具有排序检索功能的隐藏向量加密方面，进一步提高隐藏向量加密的安全性与实用性.

[1]Wang Jie, Yu Xiao, Zhao Ming. Privacy-preserving ranked multi-keyword fuzzy search on cloud encrypted data supporting range query[J]. Arabian Journal for Science and Engineering, 2015, 40(8): 2375-2388

[2]Xu Qunqun, Shen Hong, Sang Yingpeng, et al. Privacy-preserving ranked fuzzy keyword search over encrypted cloud data[C] //Proc of the 14th Int Conf on Parallel & Distributed Computing, Application and Technologies. Los Alamitos, CA: IEEE Computer Society, 2013: 239-245

[3]Li Jin, Wang Qian, Wang Cong, et al. Fuzzy keyword search over encrypted data in cloud computing[C] //Proc of the 29th IEEE INFOCOM 2010. Piscataway, NJ: IEEE, 2010: 1-5

[4]Liu Chang, Zhu Liehuang, Li Longyi, et al. Fuzzy keyword search on encrypted cloud storage data with small index[C] //Proc of the 1st IEEE Int Conf on Cloud Computing and Intelligence Systems. Piscataway, NJ: IEEE, 2011: 269-273

[5]He Tuo, Ma Wenping. An efficient fuzzy keyword search scheme in cloud computing[C] //Proc of the 2nd Int Conf on Intelligent Networking and Collaborative Systems. Piscataway, NJ: IEEE, 2013: 786-789

[6]Park D J, Kim K, Lee P J. Public key encryption with conjunctive field keyword search[G] //LNCS 3325: Information Security Applications. Berlin: Springer, 2005: 73-86

[7]Hwang Y H, Lee P J. Public key encryption with conjunctive keyword search and its extension to a multi-user system[G] //LNCS 4575: Proc of the 1st Int Conf on Pairing-Based Cryptography. Berlin: Springer, 2007: 2-22

[8]Zhang Bo, Zhang Fangguo. An efficient public key encryption with conjunctive-subset keywords search[J]. Journal of Network and Computer Applications, 2011, 34(1): 262-267

[9]Shen E, Shi E, Waters B. Predicate privacy in encryption systems[G] //LNCS 5444: Theory of Cryptography Conference. Berlin: Springer, 2009: 457-473

[10]Li Zhen, Jiang Han, Zhao Minghao. A discretionary searchable encryption scheme in multi-user settings[J]. Journal of Computer Research and Development, 2015, 52(10): 2313-2322 (in Chinese)

(李真, 蒋瀚, 赵明昊. 一个自主授权的多用户可搜索加密方案[J]. 计算机研究与发展, 2015, 52(10): 2313-2322)

[11]Caro A D, Iovino V, Persiano G. Fully secure hidden vector encryption[G] //LNCS 7708: Proc of the 5th Int Conf on Pairing-Based Cryptography. Berlin: Springer, 2012: 102-121

[12]Iovino V, Persiano G. Hidden-vector encryption with groups of prime order[G] //LNCS 5209: Proc of Int Conf on Pairing-Based Cryptography. Berlin: Springer, 2008: 75-88

[13]Mitsuhiro H, Takato H, Takashi I, et al. Ciphertext-policy delegatable hidden vector encryption and its application to searchable encryption in multi-user setting[G] //LNCS 7089: Proc of the 13th IMA Int Conf on Cryptography and Coding. Berlin: Springer, 2011: 190-209

[14]Yang Yang, Mao Maode. Conjunctive keyword search with designated tester and timing enabled proxy re-encryption function for e-health clouds[J]. IEEE Trans on Information Forensics and Security, 2016, 11(4): 746-759

[15]Keita E, Atsuko M, Kazumasa O. A timed-release proxy re-encryption scheme and its application to fairly-opened multicast communication[G] //LNCS 6402: Proc of the 4th Int Conf on Provable Security. Berlin: Springer, 2010: 200-213

[16]Liu Qin, Wang Guojun, Wu Jie. Time-based proxy re-encryption scheme for secure data sharing in a cloud environment[J]. Information Sciences, 2014, 258(3): 355-370

[17]Liang Kaitai, Huang Qiong, Roman S, et al. A conditional proxy broadcast re-encryption scheme supporting timed-release[G] //LNCS 7863: Information Security Practice and Experience. Berlin: Springer, 2013: 132-146

[18]Rhee H S, Park J H, Lee D H. Generic construction of designated tester public-key encryption with keyword search[J]. Information Sciences, 2012, 205(1): 93-109

[19]Rhee H S, Susilo W, KiM H J. Secure searchable public key encryption scheme against keyword guessing attacks[J]. IEICE Electronics Express, 2009, 6(5): 237-243

[20]Katz J, Sahai A, Waters B. Predicate encryption supporting disjunctions, polynomial equations, and inner products[G] //LNCS 4965: Proc of the EUROCRYPT 2008. Berlin: Springer, 2008: 146-162

[21]Lewko A, Okamoto T, Sahai A, et al. Fully secure functional encryption: Attribute-based encryption and (hierarchical) inner product encryption[G] //LNCS 6110: Advances in Cryptology-EUROCRYPT 2010. Berlin: Springer, 2010: 62-91

[22]Okamoto T, Takashima K. Adaptively attribute-hiding (hierarchical) inner product encryption[G] //LNCS 7237: Advances in Cryptology-EUROCRYPT 2012. Berlin: Springer, 2012: 591-608

[23]Okamoto T, Takashima K. Fully secure functional encryption with general relations from the decisional linear assumption[G] //LNCS 6223: Advances in Cryptology-CRYPTO 2010. Berlin: Springer, 2010: 191-208

[24]Park J H. Inner-product encryption under standard assumptions[J]. Designs, Codes and Cryptology, 2011, 58(3): 235-257

[25]Boneh D, Waters B. Conjunctive, subset, and range queries on encrypted data[G] //LNCS 4392: Proc of the 4th Int Conf on Theory of Cryptology. Berlin: Springer, 2007: 535-554

[26]Boyen X. A tapestry of identity-based encryption: practical frameworks compared[J]. International Journal of Applied Cryptography, 2008, 1(1): 3-21

[27]Park J H. Efficient hidden vector encryption for conjunctive queries on encrypted data[J]. IEEE Trans on Knowledge and Data Engineering, 2011, 23(10): 1483-1497

[28]Park J H, Lee K S, Susilo W, et al. Fully secure hidden vector encryption under standard assumptions[J]. Information Sciences, 2013, 232(5): 188-207

[29]Park J H, Lee D H. A hidden vector encryption scheme with constant-size tokens and pairing computations[J]. IEICE Trans on Fundamentals of Electronics Communications & Computer Sciences, 2010, 93-A(9): 1620-1631

[30]Lee K, Lee D H. Improved hidden vector encryption with short ciphertext and tokens[J]. Designs, Codes and Cryptology, 2011, 58(3): 297-319

[31]Baek J, Nani R S, Susilo W. Public key encryption with keyword search revisited[G] //LNCS 5072: Proc of 2008 Int Conf on Computational Science and Its Applications. Berlin: Springer, 2008: 1249-1259

[32]Guo Lifeng, Yau Weichuen. Efficient secure-channel free public key encryption with keyword search for EMRs in cloud storage[J]. Journal of Medical Systems, 2015, 39(2): 1-11

[33]Rhee H S, Park J H, Susilo W, et al. Trapdoor security in a searchable public-key encryption scheme with a designated tester[J]. Journal of Systems and Software, 2010, 83(5): 763-771

[34]Shi E, Waters B. Delegating capabilities in predicate encryption systems[G] //LNCS 5126: Proc of the 35th Int Colloquium on Automata, Languages, and Programming. Berlin: Springer, 2008: 560-578

[35]Shao Jun, Cao Zhenfu, Liang XIaohui, et al. Proxy re-encryption with keyword search[J]. Information Sciences, 2010, 180(13): 2576-2587

[36]Yau W C, Phan C W, Heng S H, et al. Proxy re-encryption with keyword search: New definitions and algorithms[G] //LNCS 122: Security Technology, Disaster Recovery and Business Continuity. Berlin: Springer, 2010: 149-160

[37]Fang Liming, Susilo W, Ge Chunpeng, et al. Chosen-ciphertext secure anonymous conditional proxy re-encryption with keyword search[J]. Theoretical Computer Science, 2012, 462(1): 39-58

[38]Wang Xuan, Huang Xinyi, Yang Xiaoyuan, et al. Further observation on proxy re-encryption with keyword search[J]. Journal of Systems and Software, 2012, 85(3): 643-654

[39]Bellare M, Boldyreva A, Palacio A. An uninstantiable random oracle-model scheme for a hybrid-encryption problem[G] //LNCS 3027: Proc of the EUROCRYPT 2004. Berlin: Springer, 2004: 171-188

[40]Li Jiguo, Shi Yuerong, Zhang Yichen. Searchable ciphertext-policy attribute-based encryption with revocation in cloud storage[OL]. [2015-02-19]. https://www.infona.pl/resource/bwmeta1.element.wiley-dac-v-30-i-1-dac2942