基于分项可变权函数的各项异性去噪模型

王锐锐，蔡光程

(昆明理工大学 理学院，云南 昆明 650500)

0 引 言

图像在获取、存储、传输、转置的过程中总是不可避免地带来乘性噪声的污染，乘性噪声不仅在较大程度上影响了图像细节的真实情况，且严重影响了图像的分割、分类、目标检测以及感兴趣区域的提取。因此，研究和发展含乘性噪声的图像复原方法具有重要的理论价值和实际意义。传统的基于Gauss分布的线性滤波器是对图像的高频区域做处理，因为边缘细节信息也在高频区域，所以在去噪的同时模糊了图像的边缘区域，丢失了大量的细节信息[1]。

基于偏微分方程(PDE)去噪模型的研究成为了近年来的热点。其基本思想是利用偏微分方程各向异性扩散理论对噪声图像做处理，通过求偏微分方程的解，达到对图像去噪的目的[2-3]。

文中讨论的乘性噪声模型为：f(x,y)=u(x,y)v(x,y)，其中点(x,y)为图像区域Ω对应的像素点，f(x,y)为观测图像，u(x,y)为待恢复图像，v(x,y)为噪声。基于该模型，利用MAP估计方法在乘性噪声服从Gamma分布的假设下，文献[4-6]介绍了AA(Aubert-Aujol)模型和HNW模型,分别如式1和式2所示：

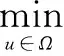
(1)

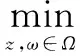
(2)

上述模型都是由正则项和保真项构成，其中λ,γ为Lagrange参数，其值主要由图像的结构和噪声的强度决定。正则项均为各项同性全变差(total variation,TV)，全变差正则项能够在保护图像边缘的同时达到有效的去噪效果，但是在处理图像时存在三点不足：降低了图像的边缘锐度；在纹理区域会出现一定程度的模糊现象；在图像的光滑区域会产生“阶梯效应”。对此，文中提出一种基于四阶微分全变差的图像去噪模型，并通过实验对其进行验证。

1 基于分项可变权函数的各项异性去噪模型的建立

基于上述模型的不足及现象产生的原因，很多学者提出了不同的解决方案[7-14]。文献[15]中提出了Hessian矩阵Frobenius范数的迭代重加权二阶正则模型，有效地抑制了图像在平坦区域产生的“阶梯效应”。

在此基础上，文中建立了一个动态局部正交坐标系，使其在对图像做降噪处理时，根据图像局部变化的不同改变对图像的去噪进度，从而在去除图像噪声的同时能够有效地保护图像的边缘细节及纹理。设动态局部正交坐标系(η,ξ)：

其中η为平行于图像梯度u的单位矢量，ξ为图像水平线集的单位切矢量[7]。在该局部坐标系中，有动态坐标系Hessian矩阵设为：所以有：

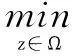
(3)

模型3由TV正则项和保真项构成，模型在去除噪声的同时也有效抑制了“阶梯效应”。g(x,y)为权函数，用来防止图像的纹理及边界模糊。

其中，ε(n)使得z(n-1)中的零值元素在下次迭代中为一个非零数，从而保证迭代的稳定。从传统权函数[16-17]的选取中可以看出其都是基于梯度模值建立的，对图像的边缘区域、平坦区域和噪声区域无法做出详细的区分，在处理图像时区域间连接处的细节纹理不能得到有效的保留。

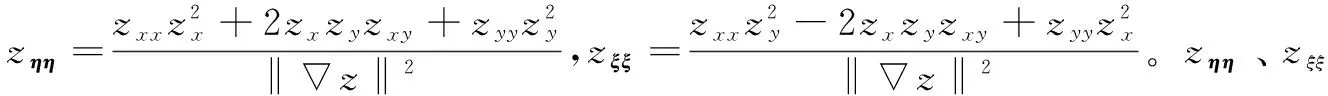
(1)若为边缘区域，那么|zηη|大，|zξξ|小，所以D大；

(2)若为平坦区域或坡道区域，|zηη|和|zξξ|均是小的，所以D小；

(3)对于噪声区域，|zηη|和|zξξ|均是大的或者几乎相等，所以D小。

(4)

式4中取B·2z的F-范数并对其平方：

所以分项加权可变权函数为：

f(η,ξ)e-z(η,ξ))dηdξ}

(5)

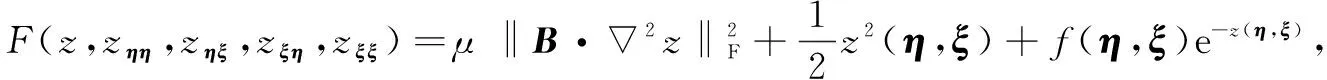
2 模型求解

由模型5知：

EMT患者卵泡早期孕激素水平升高，影响卵泡下个周期的发育，并干扰卵巢颗粒细胞黄体生成素受体形成，影响排卵及胚胎着床，从而引起不孕；此外研究还发现，EMT患者子宫内膜中HOXA10表达缺陷，而HOXA10对胚胎发育和子宫内膜容受性至关重要，推断EMT患者通过影响内膜形成降低了胚胎的着床率[26]。

Fz=z(η,ξ)-f(η,ξ)-z(η,ξ)

则模型5对应的Euler方程为：

因此模型对应的梯度下降流为：

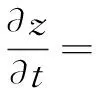
(6)

同理，其余两项可用类似的方法离散。

对三阶导数的“半点”离散得：

求得四阶导函数的离散；

其余的三阶、四阶导数可用同样的方法求得。

对于系数的“半点”处的值，可用相邻的两个整点的平均值近似：

此离散的边界条件为：

3 实验结果与分析

为了验证算法对图像去噪的有效性，选择传统的高斯去噪、二阶的ATV去噪算法及四阶ATV去噪算法进行对比，用峰值信噪比PSNR(PSNR=10×lg(2552/MSE),MSE=‖z0-z‖2)和结构相似度(SSIM)作为衡量标准。处理的图片用到了彩色图像Rose和灰白图像Room。经过大量的数值模拟实验，模型参数取：μ=1/4、a=0.4、b=0.7，迭代步长Δt=1.12，迭代次数n=100，当图像迭代精度ε=10-4时，处理效果最佳。

图1和图2分别是Rose图像和Room图像的去噪结果。

图1 四种去噪结果(Rose图像)

图2 四种去噪结果(Room图像)

表1和表2分别是两幅图像的算法对比结果。

表1 算法比较结果(Rose图像)

表2 算法比较结果(Room图像)

由图像及峰值信噪比、结构相似度的对比可知，传统的高斯去噪模型在去除噪声的同时，模糊了整幅图像，使得图像在处理后难以分辨其特征。而二阶的ATV模型在去噪时，图像的边缘信息保护较好，但恢复图像存在“阶梯效应”。而四阶ATV模型在边缘的细节保留和对“阶梯效应”的抑制都有不错的效果，但丢失了图像不同区域的过渡信息。文中模型在去除噪声时不仅有效保留了图像的边缘及不同区域之间的纹理信息，而且更好地抑制了“阶梯效应”的产生，从而证明了该模型的有效性。

4 结束语

文中利用一个边缘指标有效地区分了边缘区域和平滑区域，基于这个新的边缘指标设计了一个可变的权函数矩阵，提出了一种各项异性的可变权函数的去噪模型，并用梯度下降法进行求解。实验结果及数据表明，该模型能够衰减噪声后的“阶梯效应”，同时较好地保留了图像的细节信息及不同区域间的过渡信息。由于对不同区域做出了区分，有效地提高了模型的迭代速度。

参考文献：

[1] 冈萨雷斯.数字图像处理[M].阮秋琦,译,第2版.北京:电子工业出版社,2003:169-174.

[2] 王大凯,侯榆青,彭进业.图像处理的偏微分方程方法[M].北京:科学出版社,2008:110-139.

[3] 丁 畅,尹清波,鲁明羽.数字图像处理中的偏微分方程方法综述[J].计算机科学,2013,40(11A):341-346.

[4] AUBERT G, AUJOL J. A variational approach to removing multiplicative noise[J].SIAM Journal on Applied Mathematics,2008,68(4):925-946.

[5] SHI Jianing, OSHER S.A nonlinear inverse scale space method for a convex multiplicative noise model[J].SIAM Journal on Imaging Sciences,2008,1(3):294-321.

[6] HUANG Yumei,MICHAEL K N,WEN Youwei.A new total variation method for multiplicative noise removal[J].SIAM Journal on Imaging Sciences,2009,2(1):20-40.

[7] 袁泽剑，郑南宁，张元林，等.一种非线性扩散滤波器的设计方法及其应用[J].计算机学报，2002，25(10)：1072-1076.

[8] LIU Chunxiao, ZHU Shengfeng. A convex relaxation method for computing exact global solutions for multiplicative noise removal[J].Journal of Computational and Applied Mathemmatics，2013，238:144-155.

[9] WEICKERT J.Anisotropic diffusion in image processing[C]//European consortium for mathematics in industry.Germany:B. G. Teubner,Stuttgart,1998.

[10] 王旭东,冯象初,白 键.基于结构张量场拟合的图像恢复方法[J].西安电子科技大学学报:自然科学版,2011,38(6):68-74．

[11] 许建楼,冯象初,郝 岩.二阶总广义变分图像修复模型及其算法[J].西安电子科技大学学报:自然科学版,2012,39(5):18-23.

[12] 王 璐.基于四阶微分全变差的图像去噪模型[J].计算机技术与发展,2016,26(3):85-88.

[13] 艾 立.基于变分和偏微分方程的图像去噪研究[D].成都:电子科技大学,2015.

[14] 张化朋,任少美.基于偏微分方程的乘性噪声去噪算法[J].计算机技术与发展,2016,26(11):90-92.

[15] 王旭东,冯象初,张选德.去除乘性噪声的迭代重加权二阶正则模型[J].西安电子科技大学学报:自然科学版,2014，41(2)：130-136.

[16] 周先春,汪美玲,石兰芳,等.基于小波与重调和方程的扩散去噪模型的研究[J].物理学报,2015,64(6):064203.

[17] 张小燕,吐尔洪江·阿布都克力木.小波变换的阈值图像去噪算法改进[J].计算机技术与发展,2017,27(3):81-84.