“火星探路者”舱伞系统动力学特性仿真研究

，，

北京空间机电研究所，北京 100094

与地球相比，火星上大气密度非常稀薄。在离火星表面10 km高度处其大气密度约为0.006 5 kg/m3，而在离地球表面10 km高度处的大气密度约为0.413 kg/m3，即火星上的大气密度要比地球上的小两个数量级。火星重力加速度比地球小，约为地球相同高度的38%左右。所以火星探测器在火星表面实现软着陆，一般通过其自身的气动外形、降落伞和着陆制动等综合减速和缓冲方案来完成[1-2]。

舱伞系统减速下降过程中航迹及姿态的计算对于系统的性能评估十分重要，减速下降过程中的动力学特性将对系统的工作时序、一些敏感装置的工作可靠性产生较大的影响，是安全着陆的基本保证。以往的舱伞系统运动特性研究一般都是针对两体系统，国内外对两体模型的动力学建模方法及研究较为成熟，掌握了从2自由度到12自由度的建模方法[3]。对于“火星探路者”这种“降落伞-后锥体-着陆器”组成的三体系统，截至目前，在国内公开发表的论文中未见有关动力学建模及运动特性分析的相关研究。国外公开发表的文献中，文献[4]在“降落伞-后锥体-着陆器”三体物理模型基础上，考虑降落伞、后锥体、着陆器的气动阻力，对降落伞阻力系数进行了重构；文献[5]研究了“火星探路者”舱伞系统的动力学特性，认为降落伞、后锥体和着陆器组成复杂的双摆系统，建模非常困难，在降落伞初步设计阶段可对这一问题进行适当简化，因此未考虑着陆器分离展开之后的着陆器/后锥体组合体的气动特性；文献[6]描述了“火星探路者”舱伞系统终端下降阶段三体系统的组成结构；文献[7]采用ADAMS软件建立了“火星探路者”舱伞系统运动全过程的动力学模型，并利用试验数据对模型进行了验证，对三体系统的运动模式进行了分析，但并未对舱伞系统运动过程的动力学特性进行分析。单凭国外公开发表的文献，以及存在技术保密问题，无法获取“火星探路者”舱伞三体系统运动过程动力学特性的详细数据。

本文以“火星探路者”为研究对象，针对其复杂的系统和约束条件，建立了舱伞系统工作全过程的动力学模型，包括降落伞拉直、充气、全张满、抛防热大底、着陆器与后锥体分离等过程，并对舱伞系统的速度、轨迹、运动姿态、开伞力等运动学及动力学特性进行仿真研究，全面研究舱伞系统减速下降过程的运动学特性和动力学特性，可为中国开展火星探测器的研制工作提供必要的基础数据和技术支撑。

1 舱伞系统动力学模型的建立

“火星探路者”舱伞系统的减速下降过程分为两体系统下降段和三体系统下降段。图1为“火星探路者”减速着陆系统工作过程。

图1 “火星探路者”减速着陆系统工作过程[6]Fig.1 Mars Pathfinder deceleration andlanding system working process

进入舱进入火星大气层，下降到离火星表面一定高度时降落伞开伞并快速充满，以“降落伞-进入舱”组成的两体系统减速下降(如图1(a)所示)，然后防热大底分离(如图1(b)所示)，着陆器从后锥体分离展开(如图1(c)所示)，之后以“降落伞-后锥体-着陆器”组成的三体系统稳定下降(如图1(d)所示)。当着陆器下降到离火星表面一定高度时气囊充气，在离火星表面约几十米高时反推火箭工作，之后吊索切断，着陆器在气囊的保护下在火星表面着陆并开始探测。

根据“火星探路者”舱伞系统的工作过程，需要建立包括降落伞拉直、充气、全张满、抛防热大底、着陆器与后锥体分离等过程的动力学模型。

1.1 进入舱动力学模型

进入舱采用一般刚体动力学方程[8]，忽略附加质量和附加质量变化率对进入舱运动的影响：

(1)

1.2 降落伞动力学模型

降落伞的一般动力学方程为：

(2)

对在火星大气中作非定常运动的降落伞进行动力学建模时，附加质量效应是必须考虑的。设ΦBp为降落伞自身的惯量矩阵，ΦF为降落伞的附加惯量矩阵，则降落伞的广义惯量矩阵Φp可表示为：

Φp=ΦBp+ΦF

(3)

1.3 约束模型

考虑到伞绳和吊带材料的非线性弹性效应，为简化分析，作出如下假设：

1)近似取吊带与伞衣轴线之间的夹角为0°。吊带通过旋转接头与吊索相连，因此降落伞与进入舱的旋转速率完全独立，不发生耦合。

2)不考虑伞绳和吊带材料的阻尼及塑性，伞绳和吊带的张力P是应变ε的非线性函数。

3)将垂挂吊索视为刚性绳，认为其固连于进入舱上。

伞绳和吊带的张力为：

(4)

1.4 降落伞拉直阶段分析模型

舱伞系统运动仿真重点关注的是舱伞系统的运动轨迹、速度、过载、开伞力等参数，因此降落伞拉直阶段分析模型可采用简单的直线拉出模型。

将伞包视为一个变质量质点，根据变质量动力学基本原理，其动力学方程为：

(5)

式中：mb为伞包质量；vb为伞包速度；Fb为作用在伞包上的约束力；m′为伞绳/伞衣的线密度；u为伞系统从伞包中拉出的速度。

拉出速度u可表示为：

(6)

式中：rb、re和vb、ve分别为拉直过程中伞包和进入舱的位置和速度。

根据变质量质点基本方程，拉直约束力T可表示为：

(7)

式中：Fsh为伞系统的拉出阻力。

1.5 降落伞充气阶段分析模型

降落伞充气阶段视为“降落伞-进入舱”12个自由度的两体模型。根据“火星探路者”伞衣阻力面积变化曲线[9](如图2所示)拟合出伞衣阻力面积随时间变化的函数为：

(8)

式中：CSs为充满伞衣的阻力面积；CS为伞衣充气过程中的阻力面积；tm为充满时间；t为充气时间；CS/CSs为无量纲阻力面积；t/tm为无量纲充气时间。

充满时间采用美国根据大量飞行试验总结的经验公式[9]：

(9)

式中：D0为伞衣名义直径；Vi为开始充气时的系统初始速度；A、B分别为从试验数据中获取的经验系数。

图2 伞衣阻力面积变化Fig.2 Drag area of canopy

1.6 两体下降阶段分析模型

舱伞系统的两体下降阶段包括降落伞全张满阶段、抛防热大底、抛防热大底后的飞行阶段。

全张满阶段的降落伞通过吊挂系统与进入舱连接，降落伞与进入舱之间既存在相互约束又存在相对运动，是一个典型的多体系统。与充气阶段类似，全张满阶段的舱伞系统仍视为“降落伞-进入舱”12个自由度的两体模型，其动力学模型与充气阶段的模型基本一致，区别在于降落伞动力学模型中无需考虑降落伞附加质量的变化率。

抛防热大底相当于给进入舱一个反向冲量。防热大底分离后，进入舱的质量特性发生改变。抛防热大底后系统的动力学模型与伞全张满阶段一致。

1.7 三体下降阶段分析模型

着陆器离开后锥体，系统模型由“降落伞-进入舱”两个刚体的运动变为“降落伞-后锥体-着陆器”3个刚体的运动，共18个自由度。

着陆器通过安装在其内部的下降速率限制器(Descent Rate Limiter，DRL)与后锥体分离。下降速率限制器的阻力线缠绕在磁鼓上，一端连接后锥体，另一端连接着陆器。着陆器与后锥体分离过程中，吊索不断展开。下降速率限制器阻力线产生的阻尼力与分离速度成正比[10]：

(10)

(11)

式中：d为阻力线的拉直长度；L为阻力线总长度；s为阻力线的初始松弛部分；R0为初始磁鼓半径；R1为最终磁鼓半径。

三体系统动力学模型包括以下几个部分：

1)降落伞动力学模型及其约束力与伞全张满阶段相同。

2)着陆器动力学模型与进入舱动力学模型基本一致，区别在于着陆器与进入舱相比，其质量特性和气动外形均发生了变化，约束力由吊带张力变为吊索张力。

3)不考虑吊索材料的阻尼和塑性。吊索张力是应变的非线性函数，见公式(4)。

4)将后锥体视为6自由度刚体，其动力学模型与进入舱动力学模型基本一致，区别在于后锥体的质量特性和气动外形不同于进入舱，后锥体所受外力包括重力、气动力、吊带张力和吊索约束力。

着陆器与后锥体分离过程中，吊索约束力形式为下降速率限制器提供的阻尼力。着陆器与后锥体分离完成后，吊索约束力形式为吊索张力。

1.8 模型验证

利用“火星探路者”的相关数据进行模型验证，将本文仿真结果与文献[5]中的仿真结果进行对比来验证模型的准确性和有效性。舱伞系统结构参数、气动系数及环境参数见参考文献[9，11-13]。

图3是进入舱垂直下降速度的本文仿真结果与文献仿真结果的对比。可以看出，本文仿真结果与文献仿真结果非常接近。图4是进入舱攻角的本文仿真结果与文献仿真结果的对比。可以看出，二者基本一致，约20 s后进入舱攻角达到0°左右的配平攻角，攻角的数值振荡幅度呈周期性变化，最大值约为±6°，最小值约为±2°。造成本文仿真结果与文献仿真结果偏差的原因主要是：1)初始条件偏差；2)大气参数、结构参数等其他参数可能与文献存在一定偏差。总体而言，本文仿真结果可信，仿真模型具有较高的准确性。

图3 进入舱垂直下降速度变化对比Fig.3 Vertical velocity of vehicle

图4 进入舱攻角变化对比Fig.4 Attack angle of vehicle

2 舱伞系统动力学特性仿真分析

对“火星探路者”舱伞系统减速下降过程的动力学特性进行仿真和分析。

2.1 运动位移和速度

图5和图6是进入舱质心位移和速度的变化曲线。可以看出，从降落伞开伞至着陆的整个下降过程只有120 s左右，在短时间内要完成开伞、防热大底分离、着陆器与后锥体分离、气囊充气、反推发动机点火，以及着陆器释放等一系列时序动作。这不同于航天器再入返回地球时，舱伞系统从开伞至着陆有10 min左右的时间，具有充足的时间来完成着陆过程中的各种时序动作。从降落伞开伞到系统达到稳降速度所需的时间约为30 s，对应的高度损失约为3 000 m，这比地球上相同阻力面积的降落伞的稳定时间长，高度损失大。这是火星探测器减速着陆系统进行开伞点选择和工作时序设计时需要特别注意的地方，必须严格根据舱伞系统工作过程的弹道特点和动力学特性进行设计。

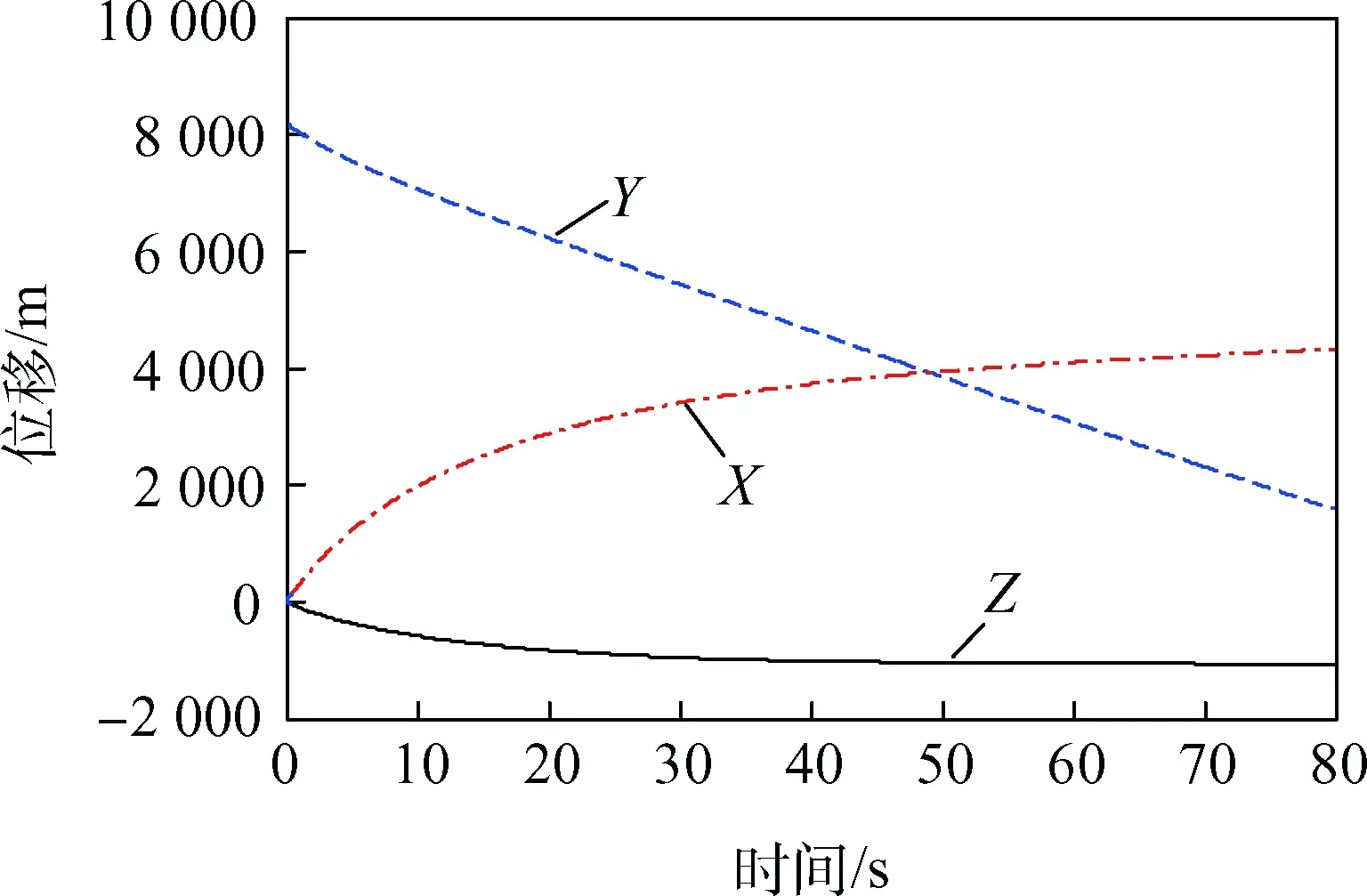
图5 进入舱位移变化Fig.5 Displacement of vehicle

图6 进入舱速度变化Fig.6 Velocity of vehicle

2.2 运动姿态

图7～图8为舱伞系统姿态角和摆角的变化曲线。可以看出，进入舱俯仰角从最初的-20°左右最终稳定在-80°左右所需的时间约为60 s，同时其摆角(定义为进入舱纵轴与垂直方向的夹角)也从最初的70°左右最终稳定在10°左右。进入舱摆角的摆动幅度较大，稳定后着陆器的最大摆角超过了20°，这对于着陆器上对地测量有角度要求的敏感器的工作是不利的。进入舱姿态稳定需要的时间比速度稳定的时间要晚30 s左右，这也是火星探测器减速着陆系统进行时序设计时需要注意的地方。

图7 系统姿态角变化Fig.7 Attitude angle of system

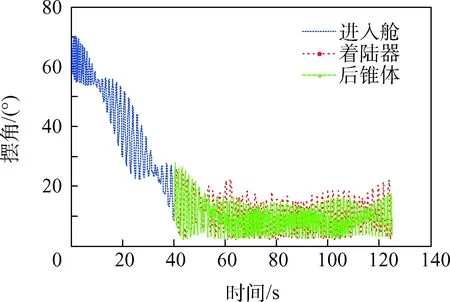
图8 系统摆角变化Fig.8 Swing angle of system

图9～图10是舱伞系统姿态角速度和合角速度的变化曲线。可以看出，后锥体的姿态角速度比着陆器的姿态角速度大，说明后锥体姿态变化比着陆器更加剧烈。在着陆器与后锥体开始分离时(约40 s)，后锥体的角速度突然增大，这是分离动作产生的扰动。分离过程中(约40～50 s)，着陆器的角速度变化幅度明显小于后锥体，这是由于着陆器在下降速率限制器的作用下平稳下降。50 s左右二者的角速度再次出现一次跃升，特别是着陆器的变化更大，这是由于着陆器与后锥体分离结束，开始受吊索的张力作用，角速度的突然改变反映了这一过程。

图9 系统姿态角速度变化Fig.9 Attitude angular velocity of system

图10 系统合角速度变化Fig.10 Angular velocity of system

2.3 开伞力

开伞力是降落伞充气性能的一个重要参数，它不仅对降落伞材料的选择有很大影响，还直接影响着进入舱的最大过载。

图11是降落伞开伞力变化曲线。开伞力最大值为44.28 kN，出现在充气过程中。可以看出，伞衣张满后，开伞力不断减小，约30 s系统达到稳降速度之后开伞力保持约为2 kN的稳定值，约等于进入舱在火星上的重力。

图11 开伞力变化Fig.11 Deployment load of parachute

2.4 舱伞系统的空间关系

图12是“降落伞-后锥体-着陆器”舱伞三体系统的空间关系示意。“降落伞-后锥体-着陆器”在空间的运动好比一个复杂的双摆系统。定义降落伞体坐标系原点Op与后锥体质心Oz之间的连线与垂直方向的夹角(取锐角)为θ，在纵向平面和侧向平面内的分量分别为θ1和θ2；定义后锥体质心Oz与着陆器质心OL之间的连线与垂直方向的夹角(取锐角)为φ，在纵向平面和侧向平面内的分量分别为φ1和φ2。

图12 舱伞三体系统空间夹角示意Fig.12 Space angle of three-body system

图13为舱伞三体系统之间空间夹角的变化曲线。可以看出，纵向平面内的θ1和φ1以及侧向平面内的θ2和φ2都呈现出正弦曲线的变化形式，存在1个大周期和1个小周期，θ的大周期约为20 s，小周期约为1 s；φ的大周期约为20 s，小周期约为2 s，即夹角φ的变化周期约为夹角θ的2倍。这说明在舱伞三体系统下降过程中，后锥体-着陆器间夹角的摆动范围比降落伞-后锥体间夹角的摆动范围大，但摆动频率比降落伞-后锥体间夹角慢。

图13 舱伞三体系统之间空间夹角的变化Fig.13 Space angle of system

3 结束语

为了全面掌握“火星探路者”减速下降过程中的动力学特性，本文针对“火星探路者”舱伞系统减速下降过程的特点，建立了包括降落伞拉直、充气、伞全张满、抛防热大底、着陆器与后锥体分离等过程的舱伞系统减速下降全过程动力学模型，其中，着陆器与后锥体分离前为“降落伞-进入舱”两体12自由度动力学模型，分离后为“降落伞-后锥体-着陆器”三体18自由度动力学模型，仿真分析了舱伞系统减速下降过程的动力学特性，得出的主要结论如下：

1)在火星稀薄大气环境下，火星探测器从降落伞开伞至着陆的整个下降过程只有120 s左右，在短时间内要完成开伞、防热大底分离、着陆器与后锥体分离、气囊充气、反推发动机点火，以及着陆器释放等一系列时序动作。火星探测器从降落伞开伞到系统达到稳降速度所需的时间约为30 s，对应的高度损失约为3 000 m。这是火星探测器减速着陆系统进行开伞点选择和工作时序设计时需要注意的地方，必须严格根据舱伞系统工作过程的弹道特点和动力学特性进行设计。

2)进入舱俯仰角稳定所需的时间约为60 s，摆角的摆动幅度较大，这对于着陆器上对地测量有角度要求的敏感器的工作是不利的。进入舱姿态稳定需要的时间比速度稳定的时间要晚30 s左右，这也是火星探测器减速着陆系统进行时序设计时需要引起注意的地方。

3)在舱伞三体系统下降过程中，后锥体-着陆器间夹角的摆动范围比降落伞-后锥体间夹角的摆动范围大，但摆动频率比降落伞-后锥体间夹角慢。

以上结论可为火星探测器降落伞减速系统的设计提供必需的基础数据和重要参考。

参考文献(References)

[1] 贾贺，荣伟. 火星探测器减速着陆技术分析[J]．航天返回与遥感，2010，31(3)：6-13.

JIA H，RONG W. Mars exploration deceleration landing technology analysis[J]. Spacecraft Recovery & Remote Sensing，2010，31(3):6-13(in Chinese).

[2] 高树义，戈嗣诚，梁艳.火星盘缝带伞跨声速风洞试验研究[J].中国空间科学技术，2015，35(4):69-75.

GAO S Y，GE S C，LIANG Y. Research on transonic wind tunnel tests of Mars disk-gap-band parachutes[J]. Chinese Space Science and Technology，2015,35(4):69-75(in Chinese).

[3] 郭叔伟，董杨彪，秦子增. 舱伞系统动力学模型和讨论[J]. 航天返回与遥感，2008，29(3)：38-44.

GUO S W，DONG Y B，QIN Z Z. Dynamic model and discussion of the parachute and payload system[J]. Spacecraft Recovery & Remote Sensing，2008，29(3):38-44(in Chinese).

[4] DESAIN PRASUN，SCHOFIELD T JOHN，LISANO E MICHAEL. Flight reconstruction of the Mars Pathfinder disk-gap-band parachute drag coefficient[C]. 17th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar，Monterey，California， 19-22 May，2003.

[5] WIEKOWSKI ALLEN. Mars Pathfinder parachute system performance[C].15th Aerodynamic Decelerator Systems Technology Conference,Toulouse,France,8-11 June,1991,AIAA 99-1701.

[6] THURMAN W S. Return to the red planet：an overview of the Mars Pathfinder mission[C]. 13th AIAAAerodynamic Decelerator Systems Technology Conference，Clearwater Beach，FL，15-18 May，1995.

[7] PENG CHIA-YEN，TSANG SAIK，SMITH KENNETH. Model correlation for Mars Pathfinder entry，descent and landing simulation[C].1997 Aerospace Conference，Snowmass,USA,1-8 February,1997,IEEE.

[8] 耿长福. 航天器动力学[M]. 北京：中国科学技术出版社，2006：60-68.

GENG C F. Spacecraft dynamics[M]. Beijing：China Science &Technology Press，2006:60-68(in Chinese).

[9] EDWARD J FALLON. System design overview of the Mars Pathfinder parachute decelerator subsystem[C]. 14th AIAA Aerodynamic Decelerator Systems Technology Conference，San Francisco，CA，3-5 June，1997.

[10] ALLEN W，WALTER M，YAW T.Mars subsonic parachute technology task system overview[C]. 18th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar，Munich，Germany，23-26 May， 2005.

[11] DESAI N PRASUN，SCHOFIELD T JOJN，LISANO E MICHAEL. Flight reconstruction of the Mars Pathfinder disk-gap-band parachute drag coefficients[J]. Journal of Spacecraft and Rockets，2005，42(4):672-676.

[12] SPENCER D A，BRAUN R D. Mars Pathfinder atmospheric entry：trajectory design and dispersion analysis[J]. Journal of Spacecraft and Rockets，1996，33(5):670-676.

[13] SPENCER A DAVID，ROBERT C BLANCHARD，ROBERT D BRAUN. Mars Pathfinder entry，descent，and landing reconstruction[J]. Journal of Spacecraft and Rockets，1996，36(3):357-366.