基于能耗最优的多足机器人综合步态优化方法
2018-05-28,,2,*,,2
,,2,*,,2
1. 北京控制工程研究所,北京 100190 2. 空间智能控制技术重点实验室,北京 100190
与轮式或履带式机器人相比,足式机器人凭借更好的地形适应能力,成为移动机器人研究领域的热点之一,然而高能耗已成为制约足式机器人广泛应用和进一步发展的瓶颈问题之一[1]。影响足式机器人步行能耗的因素较多,主要包括机器人自身的结构参数和步态参数[2],当机器人结构确定后,通过设计合理的步态参数来提高步行能量效率十分必要。
保证多足机器人步态的稳定性是步态优化过程中的必要约束条件,对于多足机器人步态的稳定性研究,当前最常用的是基于机器人重心的静稳定性方法,以四足机器人慢走步态为例,该方法要求机器人重心时刻保持在支撑区域内,而为了保证一定的稳定裕度,支撑区域需要进行一定的收缩处理,这会导致连续行走时稳定支撑区域不连续,因此需要加入四足支撑阶段用于将机器人重心从上一个稳定支撑区域移动至下一个稳定支撑区域,影响机器人行走的连续性。零力矩点(Zero Moment Point,ZMP)稳定性理论[3]已广泛应用于双足机器人的平衡控制问题中,有学者指出,该理论并非双足机器人步态稳定的充分条件,只是机器人脚板不发生偏转的充分条件[4];对于多足机器人若把机器人的支撑区域理解为脚板,那么脚板不发生偏转与机器人不发生倾倒是相一致的,因此ZMP稳定性理论适用于多足机器人步态的稳定性分析。本文采用基于ZMP稳定性理论的机身轨迹规划方法,以确保步态参数优化过程中步态的稳定性。
目前针对多足机器人步态优化方面的研究主要有以下一些成果,文献[5]从仿生学的角度对四足机器人摆动腿轨迹进行了研究,文献[6]分析对比了3种特殊的足端轨迹对机器人移动能耗的影响,并未考虑步态参数对机器人运动稳定性的影响;文献[7]基于ZMP稳定性理论对四足机器人机身运动轨迹进行了优化,文献[8]为提高四足机器人爬行过程中的静稳定性和行走速度,对爬行步态进行了优化,但并未考虑到行走过程中的摆动腿轨迹和能耗优化问题;文献[9-11]虽然在步态优化过程中综合考虑了摆动腿轨迹和机身运动轨迹,但其优化对象为简化的机器人平面连杆模型,这种简化的动力学模型不能准确真实地反映足式机器人的行走过程。
针对上述分析,本文提出一种基于能耗最优的多足机器人综合步态优化方法,为了在优化过程中同时优化摆动腿轨迹、机身运动轨迹和步态参数,并且保证机器人的步态稳定性,将优化过程转换为两个嵌套的子优化问题。首先,采用一种基于ZMP稳定性理论的机身运动轨迹规划方法,针对给定的下一步落足点和支撑多边形,利用优化的方法规划出机身运动轨迹,在保证机身轨迹连续平滑的同时,确保机器人在迈步过程中的稳定性。其次,提出一种基于能耗指标的周期性步态参数优化方法,建立机器人虚拟样机模型作为步态优化模型,对步态参数、摆动腿足端轨迹和机身运动轨迹同时进行优化,得到使机器人前进单位距离能耗最优的步态。
1 机器人结构与坐标系建立
本文以四足机器人连续慢走步态为例研究机器人步态参数优化方法,该方法通过简单推广同样适用于其他多足机器人的相应步态。为方便描述,将机器人的四条腿按左前腿、右前腿、左后腿、右后腿的顺序进行编号,分别为腿1、腿2、腿3、腿4。连续慢走步态情况下每次仅有一条腿抬起向前迈步,另外三条腿支撑机器人身体前进,机器人不存在四足支撑躯体移动调整的过程,共有6种迈步次序,本文采用迈步次序为1-4-2-3的步态,已有研究成果表明该迈步顺序稳定性最好[12]。
机器人构型如图1所示,机器人包含4条腿,每条腿具有3个关节,分别为根关节(偏航自由度)、髋关节(俯仰自由度)和膝关节(俯仰自由度)。
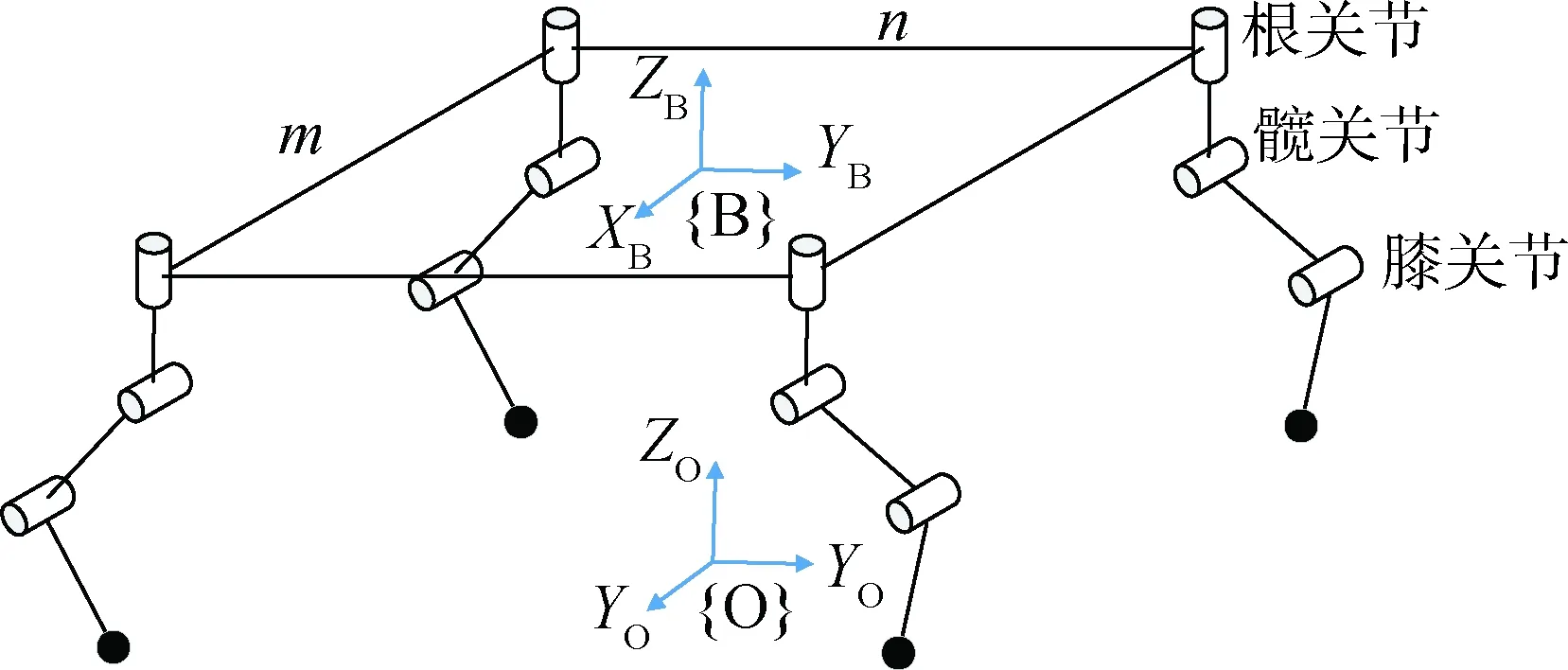
图1 四足机器人结构示意Fig.1 Structure of the quadruped robot
定义如下几个坐标系(如图1所示):机体坐标系{B}固连于机器人身体,原点位于机器人身体中心,x轴指向机器人右方,y轴指向机器人正前方,z轴垂直于身体向上;轨迹规划坐标系{O}原点位于机器人身体中心在地面的投影点,y轴为机体坐标系的y轴在水平面的投影方向,z轴垂直向上,x轴方向满足右手坐标系法则。
2 机身运动轨迹规划方法
本节采用一种基于ZMP稳定性理论的机身运动轨迹规划方法,利用当前足端位置和下一步的落足点,生成机身运动轨迹,其主要思想如下:针对给定的下一步落足点和支撑多边形,规划一条机身运动轨迹,保证机身轨迹连续平滑的同时,确保机器人在迈步过程中的稳定性。
本节后续推导如无特别说明均在轨迹规划坐标系{O}下进行,假设机身在y轴方向运动轨迹由n段分段函数描述,每段轨迹可用如下一个5次多项式表示:
hi·lyi(i=1,2,…,n)(1)
式中:ybi(t)表示机器人第i条重心轨迹;ai~fi为第i条重心轨迹多项式系数,即为待优化参数;ti为第i段轨迹内的时间变量,
lyi=[aibicidieifi]T
优化过程的目标函数取为重心轨迹的加速度平方和[13],每一段的目标函数为:
(2)
其中T为每一段轨迹的持续时间,
最终的目标函数为每一段曲线目标函数的和,因此可统一为待优化参数的二次型形式:
(3)
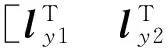
为了建立ZMP稳定性约束,考虑如下经典的近似ZMP模型[14]:
(5)
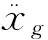
基于ZMP稳定性理论,在迈步过程中ZMP必须一直保持在机器人支撑区域内,为了保证一定的稳定裕度,支撑区域需要进行一定的收缩处理,此处可通过判断机器人ZMP与支撑三角形前后边的位置来判定机器人的步态稳定性。对于式(1)给出的重心运动轨迹,可根据式(4)求出相应的ZMP轨迹,设支撑区域可由3个支撑足端连线组成的三角形描述,在此对机器人的四条腿重新编号,令与摆动腿同侧的足端在坐标系{O}中的坐标为pa(xa,ya),摆动腿对侧的前足和后足坐标分别为pb(xb,yb),pc(xc,yc),如图2所示。以支撑三角形区域前进方向的边papb为例,ZMP稳定性约束可描述为:
(6)
式(6)可写为:
r1xZMP+r2yZMP+r3>0(7)
其中xZMP和yZMP为机器人ZMP坐标,
r1=yb-ya
r2=xa-xb
r3=(xb-xa)ya-(yb-ya)xa
将ZMP模型带入式(6),可将其改写为如下关于待优化参数的非线性不等式形式:
AiLi>-r3(8)
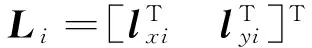

图2 支撑区域示意Fig.2 Support area in the ground reference frame
注1:对于其他多足机器人,步行过程中的稳定支持区域不一定为三角形,而是由除迈步腿外的立足点围成的多边形区域,此时同样可由式(6)形式的不等式描述步态稳定性约束条件。
为确保在迈步过程中,ZMP一直保持在机器人支撑区域内,将ZMP轨迹离散化,采样周期取为10 ms,每个时刻都必须满足上述稳定性约束。因此机身运动轨迹规划问题转化为一个目标函数为二次型形式,约束为线性约束的二次规划问题,本文采用内点法(Interior Point Method)求解[15],其基本思想是从可行域内一初始点出发,沿着可行方向,找出使目标函数下降的下一个点,保持每一个迭代点是可行域的内点,当迭代点靠近边界时,目标函数骤然增大,阻止迭代点穿越边界。优化过程的输入变量为当前机器人足端位置和下一迈步腿的落足点位置,优化过程的输出为机身运动轨迹。
本文机器人采用连续慢走步态,行走过程中支撑区域不连续,基于本节提出的机身运动轨迹规划方法,依旧可以生成一条稳定的机身运动轨迹,原因在于通过利用机器人重心加速度的跳变,可实现机器人重心轨迹连续的同时,ZMP轨迹发生跳变,由上一个稳定支撑区域跳变到下一个稳定支撑区域,如图3所示,图中虚线围成的三角形表示当前稳定支撑区域,实线围成的三角形表示下一步稳定支撑区域,空心圆形表示机器人重心,实心菱形表示机器人ZMP。
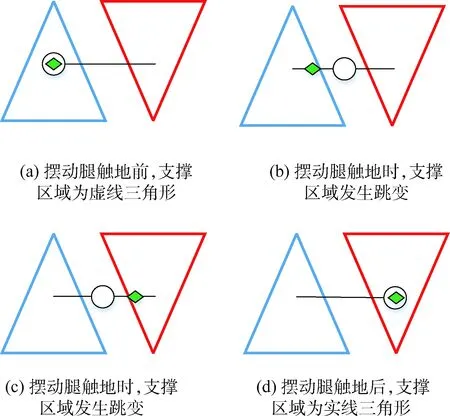
图3 机器人重心与ZMP轨迹示意Fig.3 Center of gravity and ZMP trajectoriesof the robot
3 周期性步态优化方法
利用第2节提出的机身运动轨迹规划方法,结合摆动腿轨迹,提出一种周期性步态优化方法。一个完整的步态周期由4个迈步周期组成,为简化优化问题,可令每个迈步周期的摆动腿轨迹相同。假设摆动腿足端轨迹在机身坐标系内采用贝塞尔曲线形式描述,y方向轨迹方程为:
(9)
式中:M为正整数;s=t/tw,t∈[0,tw]为每一步的时间变量,tw为摆动相时间。摆动腿足端在z方向轨迹同样可用一个上述形式的贝塞尔曲线描述,进而可根据逆运动学方程求解出各个关节轨迹[16-18]。对于连续慢走步态,当步态周期和步长确定后,可以计算出每一迈步过程中的足端位置和下一步的落足点,因此机器人重心运动轨迹可根据第2节提出的机身轨迹规划方法求得。
本文提出的周期性步态优化方法的待优化参数可用如下一个向量描述:
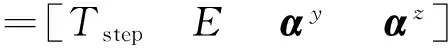
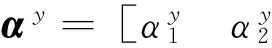
目标函数选取为前进单位距离的关节能耗,关节能耗为4条腿3个关节在整个步态周期内的能耗之和[19],计算如下:
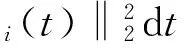
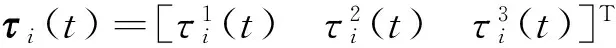
为保证机器人形成周期性平稳步态,优化过程需满足如下约束条件:
1)稳定性约束,稳定性约束可在第2节提出的机身运动轨迹优化方法上改进得到,当步态参数确定后,整个步态周期内的4个迈步落足点就可以确定,对于每个迈腿阶段,可根据第2节提出的机身运动轨迹规划方法生成一条稳定的机身运动轨迹。由于机身运动轨迹优化方法是一个凸二次规划问题,采用内点法可快速求解,因此该约束条件是可现实的。若机身轨迹优化方法无解,则表明在该步态参数下无法生成一条稳定的机身运动轨迹。
2)周期性约束,机器人的步态具有连续性和周期性,前一迈步周期的机器人运动轨迹的位置、速度和加速度终值与下一迈步周期的初值相同,此约束可表示为关于待优化参数向量的线性等式。
3)步行速度约束,每个步态周期仿真完成后,需要校验机器人整个步态周期内的平均前进速度,不小于最小前进速度:
(11)
式中:v为机器人实际前进速度;vmin为最小前进速度。
4)足端工作空间约束,足端轨迹应在机器人的足端工作空间内,并且满足一定的越障高度,即由步态参数生成的摆动腿轨迹的最大抬腿高度不小于事先设定的安全高度。
基于上述分析可知,周期性步态优化问题是一个约束非线性优化问题,可采用信赖域方法[20]进行参数寻优估计,它是一种求解非线性优化问题的有效方法,具有较强的收敛性。
4 四足机器人仿真
在ADAMS中搭建四足机器人虚拟样机,如图4所示,采用ADAMS和SIMULINK联合仿真技术进行虚拟样机仿真。机器人总质量200 kg,大腿长度0.4 m,小腿长度0.3 m。
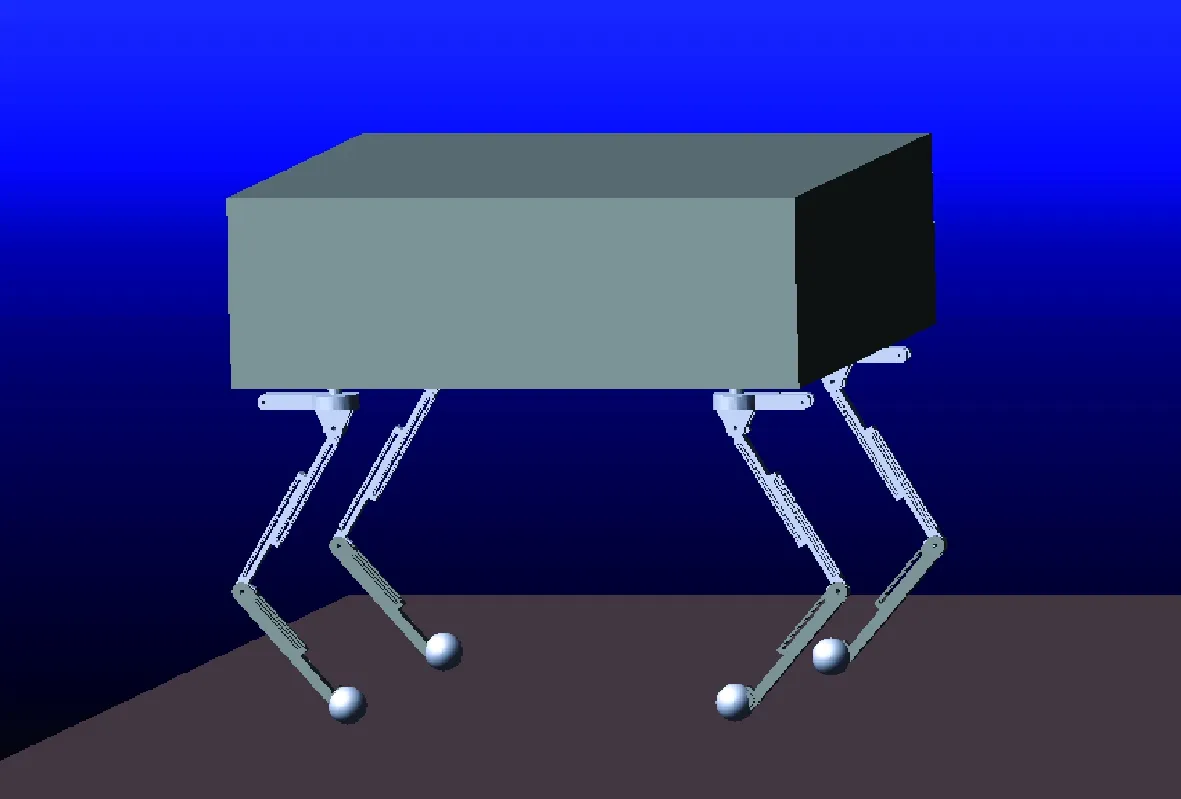
图4 四足机器人ADAMS模型Fig.4 Model of the quadruped robot in ADAMS
首先根据以往的研究和仿真经验选取一组合适的步态参数作为优化程序的初值。根据机器人足端工作空间的活动范围,综合越障高度、最长跨距和身体调整范围等指标,选取机器人初始步态参数如下:行走高度0.7 m、步长0.4 m、步态周期2 s,参考四足机器人步态研究中常用的复合摆线形式足端轨迹[21],选取贝塞尔曲线的参数使得摆动腿足段轨迹与复合摆线近似。
将上述步态参数作为优化程序的初值进行优化,优化结果见表1,优化后机器人前进单位距离能耗降低了约14%。
图5为经过优化后的一个步态周期内机身前进方向运动轨迹曲线,图6为摆动腿足端轨迹曲线。图5中点线为机器人ZMP轨迹,实线为机器人重心轨迹,点划线为前稳定区域的边界,虚线为后稳定区域的边界;前后稳定区域边界内的部分表示稳定支撑区域。机器人迈步顺序为1-4-2-3,在0.65 s时机器人由迈腿1切换至迈腿4,此时稳定支撑区域由腿2、腿3、腿4组成的后三角区域转换成由腿1、腿2、腿3组成的前三角区域,由于设定稳定裕度为0.02 m,因此在0.65 s前后机器人的稳定支持区域发生跳变且互相不接触,因此机器人ZMP轨迹发生跳变,保证ZMP一直在稳定支撑区域内。同理在1.95 s时机器人由迈腿2切换至迈腿3,机器人的稳定支持区域发生跳变。在1.3 s时,机器人由迈腿4切换至迈机身同侧的腿2,此时迈腿2前后的稳定支持区域相交,机器人ZMP轨迹保持连续。由重心轨迹可以看出,机器人在一个步态周期内重心前进距离为0.6 m,与E/β相等,表明步态具有周期性。
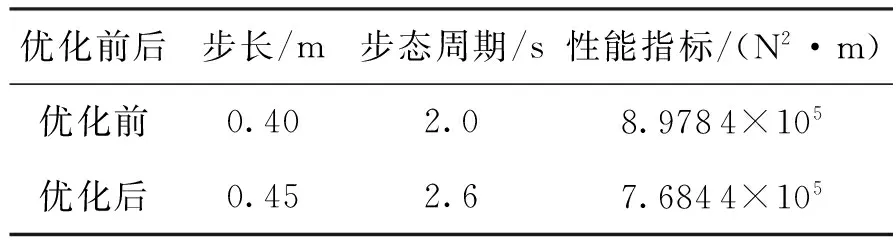
表1 步态优化结果
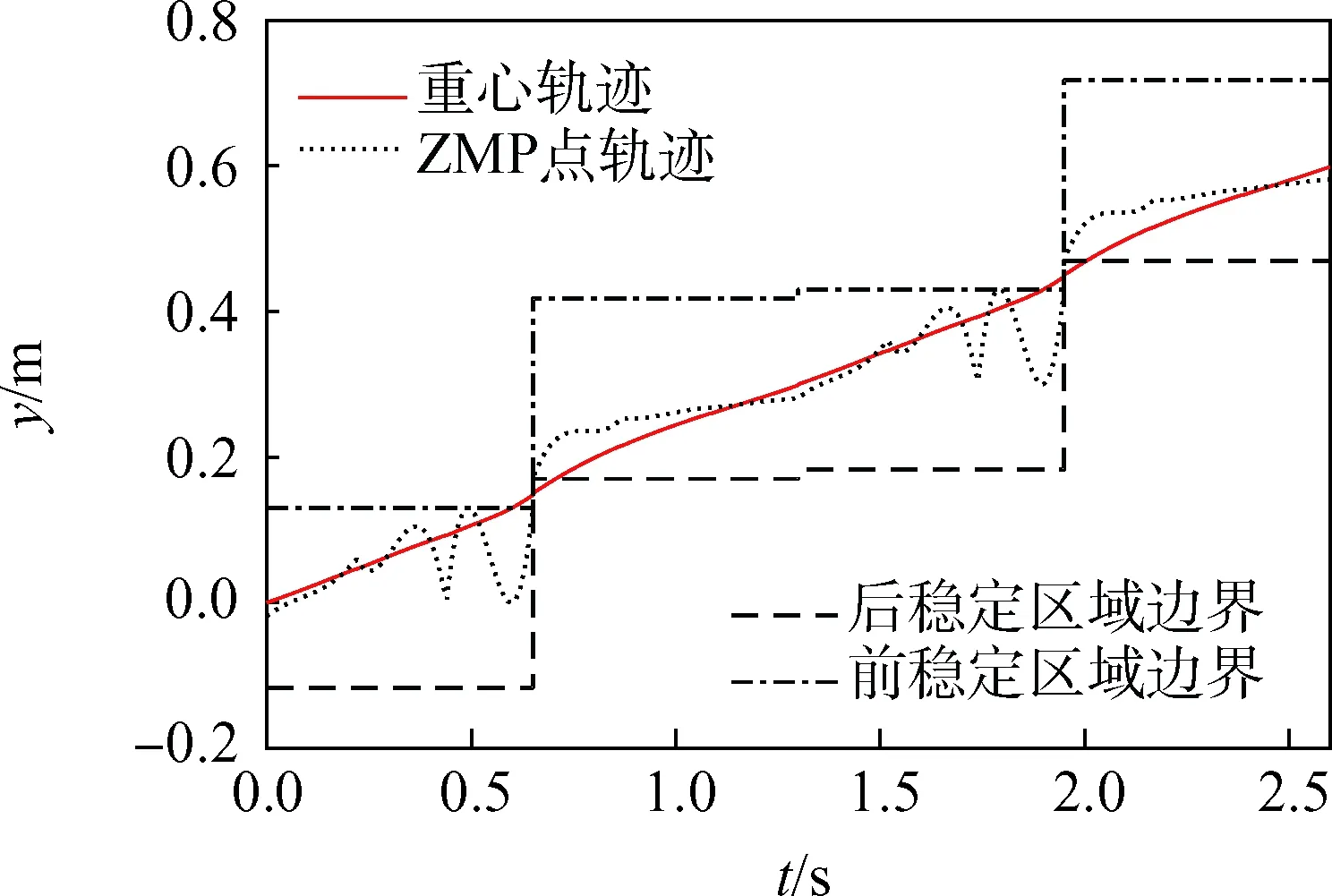
图5 机器人重心与ZMP轨迹Fig.5 Center of gravity and ZMP trajectoriesof the robot
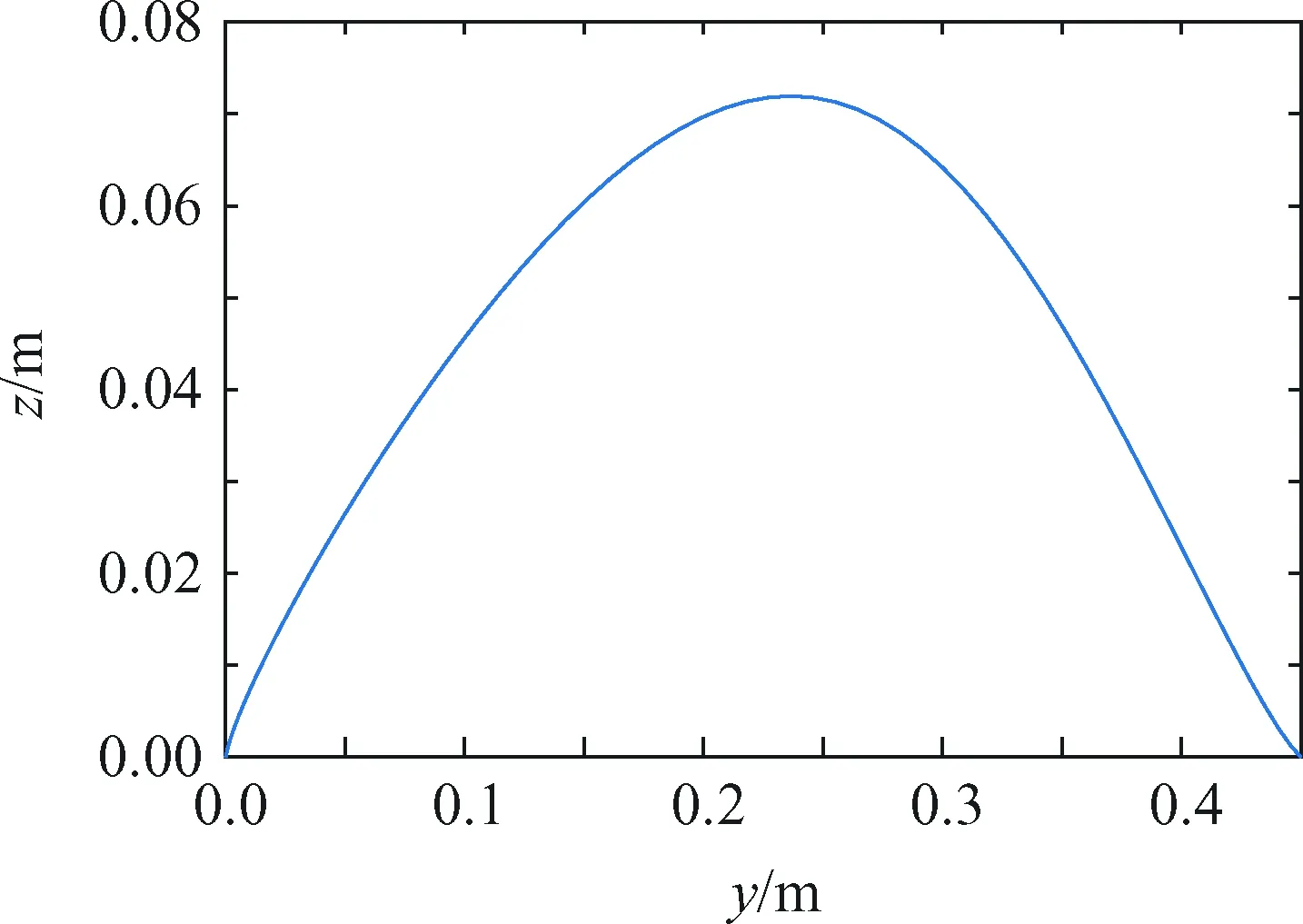
图6 摆动腿足端轨迹Fig.6 Support area in the ground reference frame
采用优化后的步态参数进行虚拟样机仿真,仿真时间设为10 s,第1 s为起始步态,机器人原地调整至周期性步态的初始状态,之后采取周期性步态前进。机器人在前进方向的位移与速度曲线如图7所示,机身俯仰角和滚转角曲线如图8所示,俯仰角和滚转角波动均在1°以内,可知,采用优化后的步态参数,机器人能平稳前进。
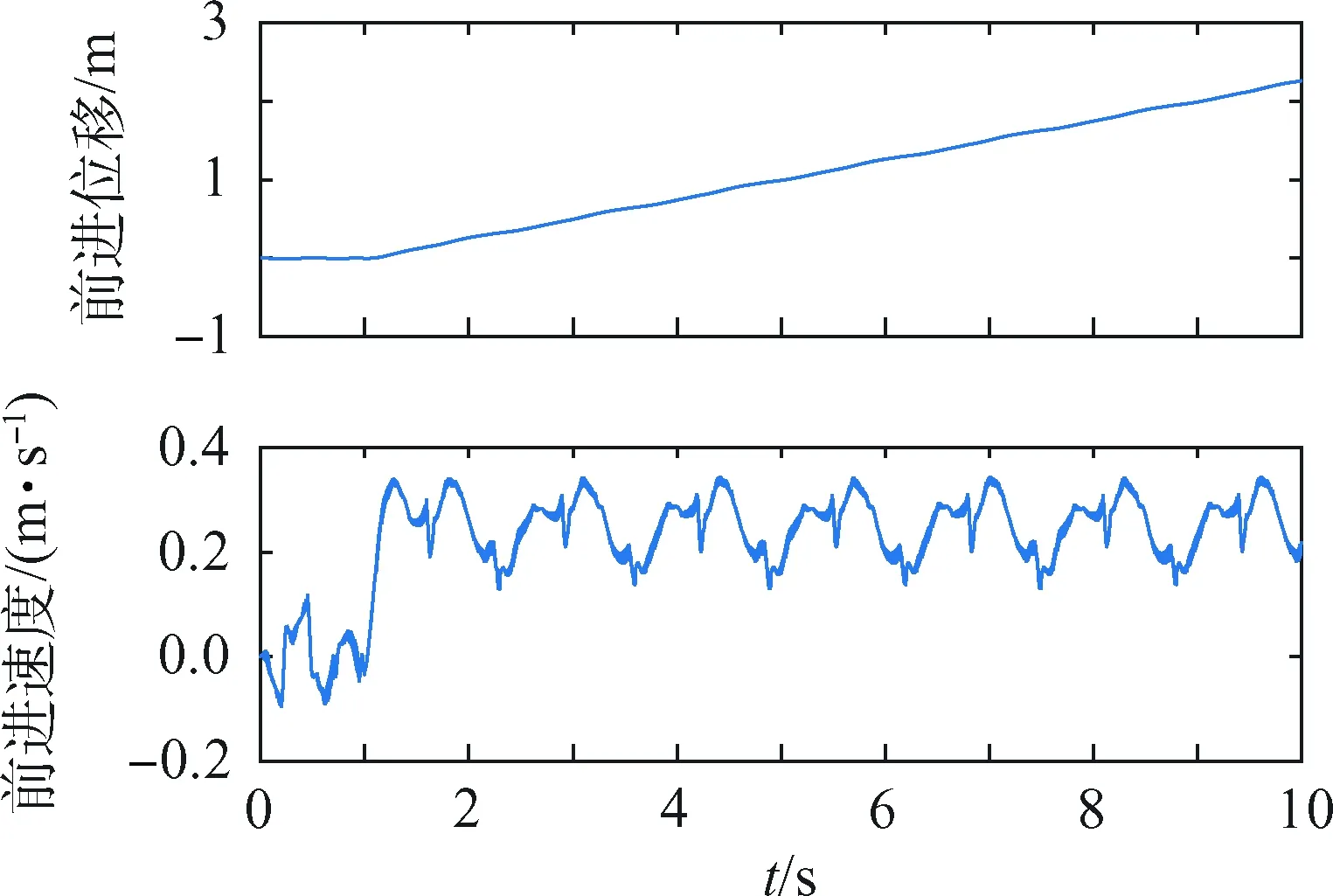
图7 机器人前进方向位移和速度Fig.7 Robot forward position and velocity
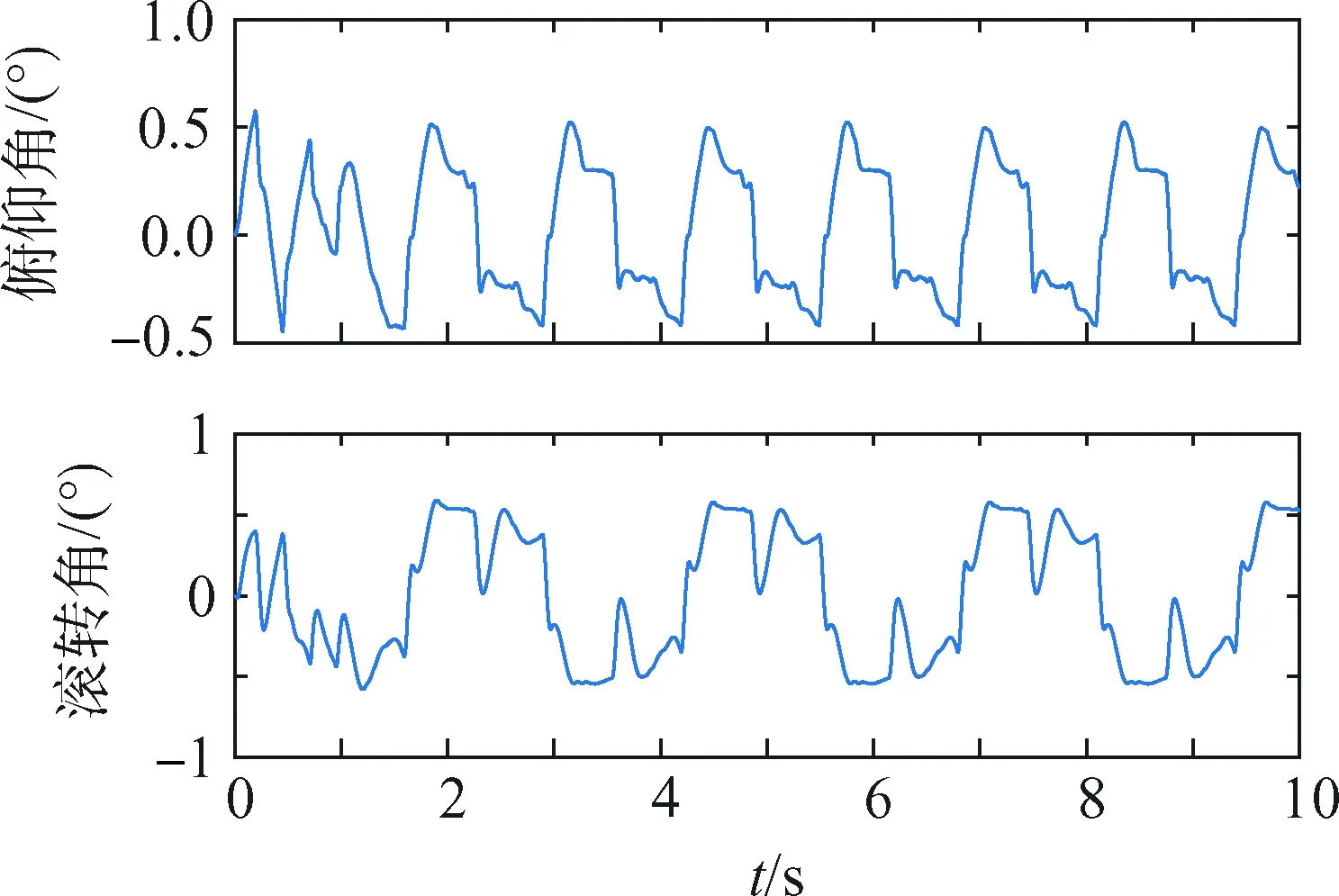
图8 机身俯仰角和滚转角Fig.8 Body pitch and roll angle
5 结束语
本文研究了一种多足机器人周期性步态优化方法,采用机器人前进单位距离的能耗作为性能指标,以四足机器人为例,建立四足机器人虚拟样机模型作为步态优化模型,对步态参数、摆动腿足端轨迹和机身运动轨迹同时进行优化,同时采用一种基于ZMP稳定性理论的机身运动轨迹规划方法保证优化过程中机器人的稳定性,最后仿真结果验证了步态优化方法的有效性。
参考文献(References)
[1] 丁良宏. BigDog四足机器人关键技术分析[J]. 机械工程学报,2015,51(7):1-23.
DING L H. Key technology analysis of BigDog quadruped robot[J]. Journal of Mechanical Engineering,2015,51(7):1-23(in Chinese).
[2] 杨亮,傅瑜,付根平,等. 基于能效优化的仿人机器人跑步步态优化与控制[J]. 计算机科学,2016,43(6):270-275.
YANG L,FU Y,FU G P,et al. Running gait planning and control for humanoid robot based on energy efficiency optimization[J]. Computer Science,2016,43(6):270-275(in Chinese).
[3] VUKOBRATOVIC M,BOROVAC B. Zero-moment point—thirty five years of its life[J]. International Journal of Humanoid Robotics,2004(1):157-73.
[4] CARON S,PHAM Q C,NAKAMURA Y. ZMP support areas for multi-contact mobility under frictional constraints[J]. IEEE Transactions on Robotics,2015,99:1-14.
[5] ASCANI S,LIBERATI F,FARABI R,et al. Horse-like walking,trotting,and galloping derived from kinematic motion primitives (kMPs)and their application to walk/trot transitions in a compliant quadruped robot[J]. Biological Cybernetics,2013,107(3):309-320.
[6] 雷静桃,王峰,俞煌颖. 四足机器人轨迹规划及移动能耗分析[J]. 机械设计与研究,2014,30(1):29-34.
LEI J T,WANG F,YU H Y. Analysis on trajectory planning and energy consumption of quadruped robot[J]. Machine Design and Research,2014,30(1):29-34(in Chinese).
[7] 刘飞,陈小平. 使用零力矩点轨迹规划的四足机器人步态进化方法[J]. 机器人,2010,32(3):398-404.
LIU F,CHEN X P. Gait evolving method of quadruped robot using zero-moment point trajectory planning[J]. Robot,2010,32(3):398-404(in Chinese).
[8] 潘少鹏,施家栋,王建中,等. 基于重心侧向摆动的四足机器人爬行步态优化[J]. 机械科学与技术,2015,34(6):821-826.
PAN S P,SHI J D,WANG J Z,et al. Crawl gait optimization for quadruped robot based on gravity center lateral movement[J]. Mechanical Science and Technology for Aerospace Engineering,2015,34(6):821-826(in Chinese).
[9] CHAE K G,PARK J H. Trajectory optimization with GA and control for quadruped robots[J]. Journal of Mechanical Science & Technology,2009,23(1):114-123.
[10] 田彦涛,孙中波,李宏扬,等. 动态双足机器人的控制与优化研究进展[J]. 自动化学报,2016,42(8):1142-1157.
TIAN Y T,SUN Z B,LI H Y,et al. A review of optimal and control strategies for dynamic walking bipedal robots[J]. Acta Automatica Sinica,2016,42(8):1142-1157(in Chinese).
[11] 王浩威. 四足机器人跳跃步态参数分析及优化研究[D]. 哈尔滨:哈尔滨工业大学,2011.
WANG H W. Parameters analysis and optimization of quadruped robot with bounding gait[D]. Harbin: Harbin Institute of Technology,2011(in Chinese).
[12] MCGHEE R B,FRANK A A. On stability properties of quadruped creeping gaits[J]. Mathematical Biosciences,1968,3(1):331-351.
[13] KALAKRISHNAN M,BUCHLI J,PASTOR P,et al. Learning,planning,and control for quadruped locomotion over challenging terrain[J]. International Journal of Robotics Research,2011,30(2):236-258.
[14] BYL K,SHKOLNIK A,PRENTICE S,et al. Reliable dynamic motions for a stiff quadruped[C]. Experimental Robotics,The Eleventh International Symposium,Athens,Greece,July 13-16,2009:319-328.
[15] 刘颖. 关于二次规划算法的研究[D]. 哈尔滨:哈尔滨师范大学,2012.
LIU Y. Research on the quadratic programming algorithm[D]. Harbin: Harbin Normal University,2012(in Chinese).
[16] 徐拴锋,杨保华,张笃周,等. 面向非合作目标抓捕的机械臂轨迹规划方法[J]. 中国空间科学技术,2014,34(4):8-15.
XU S F,YANG B H,ZHANG D Z,et al. Trajectory planning algorithm for manipulators capturing non-cooperative objects[J]. Chinese Space Science and Technology,2014,34(4):8-15(in Chinese).
[17] 古青波,李昂,赵会光. 空间双柔性机械臂刚-柔耦合建模及定标误差分析[J]. 中国空间科学技术,2017,37(1):33-40.
GU Q B,LI A,ZHAO H G. Rigid-flexible coupling modeling and calibration error analysis of the space double flexible manipulators[J]. Chinese Space Science and Technology,2017,37(1):33-40(in Chinese).
[18] 郑燕红,邓湘金,彭兢,等. 基于人工势场法的月球表层采样装置避障规划[J]. 中国空间科学技术,2015,35(6):66-74.
ZHENG Y H,DENG X J,PENG J,et al. Lunar surface sampling device collision avoidance planning based on artificial potential field method[J]. Chinese Space Science and Technology,2015,35(6):66-74(in Chinese).
[19] WESTERVELT E R,GRIZZLE J W,KODITSCHEK D E. Hybrid zero dynamics of planar biped walkers[J]. IEEE Transactions on Automatic Control,2003,48(1):42-56.
[20] 钱慧敏. 非单调信赖域算法的研究[D]. 西安:西安电子科技大学,2013.
QIAN H M. Research of nonmontone trust-region method[D]. Xi′an: Xidian University,2013(in Chinese).
[21] 王立鹏,王军政,汪首坤,等. 基于足端轨迹规划算法的液压四足机器人步态控制策略[J]. 机械工程学报,2013,49(1):39-44.
WANG L P,WANG Z J,WANG S K,et al. Strategy of foot trajectory generation for hudraulic quadruped robots gait planning[J]. Journal of Mechanical Engineering,2013,49(1):39-44(in Chinese).
