密文长度可变的Simple Matrix加密方案

2018-05-26王众韩益亮

网络与信息安全学报 2018年4期

王众，韩益亮

王众，韩益亮

（武警工程大学密码工程学院，陕西西安 710086）

多变量公钥密码是抗量子密码的可靠候选之一，其中的Simple Matrix方案是利用3个矩阵间的运算来构造的。提出了Simple Matrix方案的改进版本，通过使用具有随机二次多项式的可改变形式的扁平矩阵进行构造，使秩攻击对新的方案不可行，且代数攻击对新方案的攻击至少和求解一组随机二次方程一样困难。新的方案将密文与明文的比例改进为大于等于两倍，打破了固定不变的密文与明文比例，使其拥有一个灵活的明密文比，以适应不同的需求。

多变量公钥密码；Simple Matrix方案；明密文比；安全性分析

1 引言

公钥密码在当今的计算机安全领域扮演着十分重要的角色。传统的公钥加密方案主要基于经典数论的相关知识，比较典型的有RSA、ECC（elliptic curves cryptography）、DSA（digital signature algorithm）、属性基的公钥密码等[1]。1994年，Shor[2]提出了一种在量子计算机上运行的多项式时间算法（Shor算法），使分解大整数和求解Abel群上的离散对数问题在多项式时间内不再困难，其时间复杂度大概为(log3)（表示比特数为的数），这给基于经典数论问题的传统公钥密码学带来了威胁。而且随着计算机硬件技术的快速发展，计算机的计算能力大幅提升，在继传统计算机出现并普及后，又出现了以量子位为计算单位的计算机——量子计算机。在不久的将来，大型的量子计算机出现后，大部分传统的公钥密码将很容易被攻破。

目前，主要的抗量子密码有：基于编码的密码体制、基于格的密码体制（LWE, learning with errors）、基于Hash函数的密码体制以及基于多变量的密码体制[3]。为什么这些密码体制能够有效地抵抗量子计算机的攻击？因为它们都是在NP难问题的基础上构建起来的，而量子计算机相比于普通计算机在求解这一类问题上并没有显著的优势。抗量子密码中的基于多变量的密码体制，相比于传统的公钥密码，不仅能够有效地抵抗量子计算攻击，而且在运行的效率方面有更多的优势，并消耗更少的资源[4]。尽管存在许多实用的多变量签名方案，但有效和安全的多变量加密方案的数量还是有限的[5]。

在PQCrypto 2013会议上，Cheng等[6]提出了一种新的多变量公钥加密方案Simple Matrix（简称为ABC密码方案），它可以抵抗大部分针对多变量公钥密码方案的攻击，但是它的解密错误率却不可忽视。2014年，Ding等提出了对Simple Matrix方案的改进，即Cubic Simple Matrix密码方案[7]，使原来组成公钥的二次多变量多项式变为三次多变量多项式。这一改进，可以有效地抵抗秩攻击[8]，并且使代数攻击[8]的困难性与解决随机二次多项式系统的困难性相近。Simple Matrix方案与Cubic Simple Matrix方案都将密文与明文的比例控制在两倍关系，使其应用起来不够灵活，不能满足多种需求。本文提出了一种新的基于Simple Matrix的密码方案，在保证安全性、可靠性的同时，改变明文与密文之间的两倍固定关系，提供了一种灵活可变的明文密文比例。

2 多变量公钥密码系统以及Simple Matrix方案

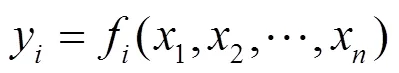
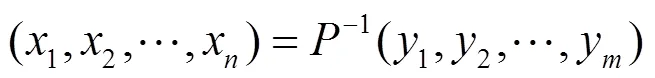
2.1 双极系统

目前，多变量密码方案可分为双极模式（bipolar）、混合模式（mixed）、多项式同构模式（IP, isomorphisms of polynomials）以及多元二次模式（MQ, multivariate quadratic）[10]。其中，大部分的多变量公钥密码是基于双极系统来构造的，混合模式的较少[11]，而另外2种则更少。

双极系统的公钥包括2部分：一是系统所在有限域以及它的域结构；二是公钥映射的个多项式。私钥则为随机选取的可逆线性仿射变换1和2，以及中心映射[12]。

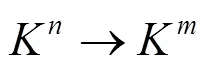
2.2 混合系统

其中，1：K→K和2：K→K的定义与双极系统中所定义的可逆线性映射相同，3则是一个K到K的可逆线性映射。

混合系统的公钥包括：1) 系统所在有限域以及其域结构；2) 构成公钥映射的多项式方程。

2.3 Simple Matrix方案

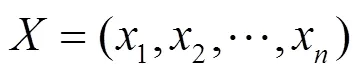
然后，定义3个小矩阵、、维度均为´，如下所示。

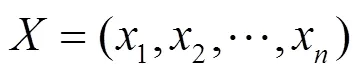
Simple Matrix算法的加密过程如下。

Simple Matrix算法的解密过程如下。

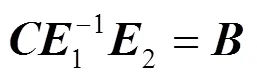
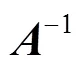
若矩阵、1、2均不可逆，则无法解密。

4) 利用可逆线性映射对进行运算，进而得到明文。

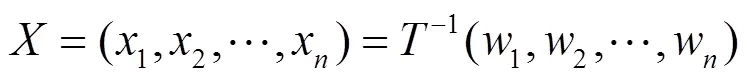
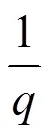
3 Simple Matrix方案改进版本

3.1 构造思想

从第2节的介绍中，可以看出Simple Matrix算法中的密文与明文比例被固定为两倍的关系，这会导致方案不够灵活，不能满足多种需求。本节提出一种改进版本，使密文与明文之间的比例更加灵活，并将其公钥由原来的二次多项式组成改为由三次多项式组成，提供了更高的安全性。

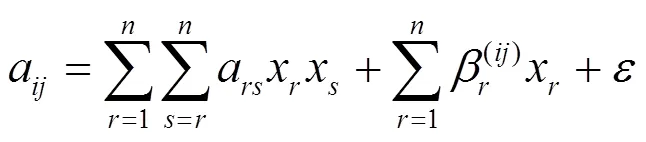
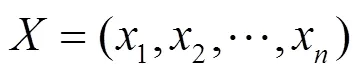
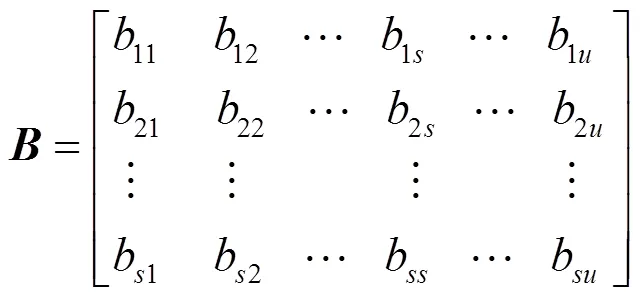
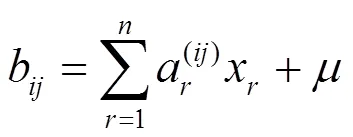
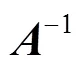
3.2 加密解密过程

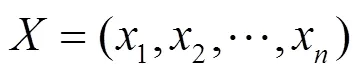
2) 解密过程如下。

若矩阵不可逆则解密失败。

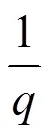
4 安全性分析

4.1 秩攻击

秩攻击是对多变量公钥密码比较有效的一种攻击方法，它分为低秩攻击（MinRank attack）[13]与高秩攻击（HighRank attack）[14]。

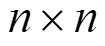
在高秩攻击中，攻击者则是找到关于中心多项式中出现次数最少的变量的线性组合。例如，Rainbow方案[15]中最后一层中的油变量，就是出现次数最少的变量，通过对每一层重复这种攻击，攻击者可以恢复可逆仿射变换，最终恢复明文。

然而，在改进版的Simple Matrix方案中，矩阵的元素是随机选择的多元二次多项式。因此，它们的秩接近于，不能使用低秩攻击。并且所有变量出现在每个中心多项式中的次数大约相同，这就不能使用高秩攻击。因此，可以得到结论，秩攻击不适用于改进版的Simple Matrix方案。

4.2 代数攻击

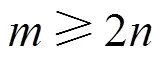
5 效率分析

5.1 明文密文比例分析

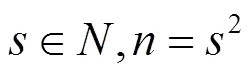
密文与明文的比例可表示为

5.2 攻击效率

下面通过实验比较直接攻击对原始版Simple Matrix方案以及改进版Simple Matrix方案的攻击效果，(,)分别代表密文与明文规模，为方便比较抵抗直接攻击的能力，令改进版Simple Matrix的密文与明文比为两倍，与原始方案保持一致，2种方案均在域GF(256)上进行。实验对比结果如表1所示。

表1 直接攻击效果对比

通过实验对比可以发现改进版Simple Matrix方案比Simple Matrix方案的求解复杂度更大，耗时更长，安全性更高，并且随着密文明文规模的扩大，消耗的时间呈指数增长。

6 结束语

Simple Matrix方案是多变量公钥密码中较新的密码体制，巧妙运用了3个矩阵间的运算来构造中心映射。本文对原始的Simple Matrix方案进行改进，将原来公钥映射中的二次多项式用三次多项式代替，可以有效地对秩攻击等攻击方法做有效的防御，提升了方案的安全性，并打破原始Simple Matrix方案中密文与明文长度两倍的固定关系，减少了明文与密文之间的一些联系，使方案更加灵活可靠。但是该改进方案中，密文长度大于等于两倍的明文长度，还需要进一步改进，使密文长度可以小于两倍的明文长度甚至小于一倍的明文长度。下一步工作是扩大明密文比例的取值范围，并提供一个加解密效率更高的方案。

[1] RIVEST R L, SHAMIR A, ADLEMAN, L. A method for obtaining digital signatures and public-key cryptosystems[J]. Communications of the ACM, 21(2), 120-126: 1978.

[2] SHOR P W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer[C]//Quantum Entanglement and Quantum Information-Proceedings of CCAST. 1999: 303-332.

[3] BERNSTEIN D J, BUCHMANN J, DAHMEN E. Post quantum cryptography[M]. Berlin Heidelberg: Springer, 2010.

[4] BOGDANOV A, EISENBARTH T, RUPP A, et al. Time-area optimized publickey engines: MQ-cryptosystems as replacement for elliptic curves?[C]//Cryptographic Hardware and Embedded Systems–CHES 2008. 2008:45-61.

[5] DING J, SCHMIDT D. Rainbow, a new multivariable polynomial signature scheme[C]//International Conference on Applied Cryptography and Network Security. 2005:164-175.

[6] CHENG T, DIENE A, TANG S, et al. Simple matrix scheme for encryption[C]//International Workshop on Post-Quantum Cryptography. 2013:231-242.

[7] DING J, PETZOLDT A, WANG L C. The cubic simple matrix encryption scheme[C]//Post-Quantum Cryptography. 2014:76-87.

[8] KIPNIS A, SHAMIR A. Cryptanalysis of the HFE public key cryptosystem[C]//Advances in Cryptology—CRYPTO’99. 1999: 19-30.

[9] SAKUMOTO K, SHIRAI T, HIWATARI H. Public-key identification schemes based on multivariate quadratic polynomials[J]. Technical Report of Ieice Isec, 2011, 111:706-723.

[10] PATARIN J. Asymmetric cryptography with a hidden monomial[C]//Advances in Cryptology—CRYPTO ’96. 1996:45-60.

[11] DING J, GOWER J E, SCHMIDT D S. Multivariate public key cryptosystems[M]. US : Springer US, 2006.

[12] 丁斗博. 多变量公钥密码中TTS方案的分析与改进[D]. 西安：西安电子科技大学, 2013.

DING D B. Analysis and improvement on the multivariate quadratic TTS scheme[D]. Xi’an: Xidian University, 2013.

[13] GOUBIN L, COURTOIS N. Cryptanalysis of the TTM Cryptosystem[C]//International Conference on the Theory and Application of Cryptology and Information Security. 2000: 44-57.

[14] COPPERSMITH D, STERN J, VAUDENAY S. Attacks on the birational permutation signature schemes[C]//Advances in Cryptology—CRYPTO’ 93. 1993:435-443.

[15] DING J, SCHMIDT D. Rainbow, a new multivariable polynomial signature scheme[C]//Applied Cryptography and Network Security. 2005:164-175.

[16] COURTOIS N, KLIMOV A, PATARIN J, et al. Efficient algorithms for solving overdefined systems of multivariate polynomial equations[C]//Advances in Cryptology—EUROCRYPT 2000. 2000: 392-407.

[17] FAUGERE J C. A new efficient algorithm for computing Gröbner bases without reduction to zero (F5)[C]//The 2002 International Symposium on Symbolic and Algebraic Computation. 2002:75-83.

[18] FAUGERE J C. A new efficient algorithm for computing Grobner bases (F4)[J]. Journal of Pure and Applied Algebra,1999,139: 61-88.

[19] DING J, BUCHMANN J. Solving degree and degree of regularity for polynomial systems over a finite fields[C]//The First International Conference on Symbolic Computation and Cryptography (SCC 2008). 2008.

[20] MOHAMED M S E, CABARCAS D, DING J, et al. MXL 3: an efficient algorithm for computing gröbner bases of zero-dimensional ideals[C]//International Conference on Information Security and Cryptology. 2009:87-100.

Simple Matrix encryption scheme with variable ciphertext length

WANG Zhong, HAN Yiliang

Engineering University of PAP, College of Cryptographic Engineering, Xi’an 710086, China

Multivariable public key cryptography is one of the reliable candidates for anti-quantum cryptography. The Simple Matrix scheme is constructed using the operations between three matrices. An improved version of the Simple Matrix scheme was proposed. It is constructed by using two flat matrices with random quadratic polynomials, so that the rank attacks is infeasible for the new scheme, and the algebraic attacks breaks the system is at least as hard as solving a set of random quadratic equations. The new scheme will improve the proportion of ciphertext and plaintext to 2 times or more, break the fixed proportion of ciphertext and plaintext, so that it has a flexible proportion to adapt to different needs.

multivariable public key cryptography, Simple Matrix scheme, the proportion of plaintext and ciphertext, security analysis

TN918.4

10.11959/j.issn.2096-109x.2018032

2018-03-10；

2018-04-01

韩益亮，hanyil@163.com

国家自然科学基金资助项目（No.61572521）

王众（1995-），男，山东泰安人，武警工程大学硕士生，主要研究方向为抗量子密码。